人教版数学八年级下册期中复习题二【精华】(含答案)
文档属性
| 名称 | 人教版数学八年级下册期中复习题二【精华】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 04:57:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册期中复习题二【精华】
一、单选题
1.(2024八下·石泉期中)如图,的顶点A,B,C在边长为1的正方形网格的格点上, 于点D,则线段的长为( )
A.4 B. C. D.5
2.(2024七下·江门期中)下列各式中,没有意义的是( )
A. B. C. D.
3.(2024八下·岳阳期末)如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
4.(2024八下·江阳期中)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
5.(2023九下·广阳月考)估计的值应在( )
A.和之间 B.和之间 C.和之间 D.和之间
6.(2022八下·兴仁月考)一旗杆在其的处折断,量得米,则旗杆原来的高度为( )
A.米 B.米 C.10米 D.米
7.(2024八下·镇海区期末)如图,在中,,于点,点在上,,若点分别为的中点,连结,,,则的长为( )
A. B. C. D.
8.(2023八下·万源月考)△ABC中,点D,G分别在边AB,AC上,点E,F在边BC上.已知DG∥BC,DE∥FG,BE=DE,CF=FG,则∠A的度数( )
A.等于90° B.等于80°
C.等于72° D.条件不足,无法计算
二、填空题
9.(2023九上·叙州期中)已知点在第四象限,化简的结果为 .
10.(2024八下·杭州月考) (化成最简二次根式).
11.(2024八下·昌邑期末)若式子在实数范围内有意义,则的取值范围是 .
12.(2024八下·永春期中)如图,在平行四边形中,平分,交于点,平分,交于点,,,则的长为 .
13.(2024八上·盐城月考)《九章算术》提供了许多勾股数如,等,其中一组勾股数中最大的数称为“弦数”.经研究,若是大于1的奇数,把它平方后拆成相邻的两个整数,则与这两个数组成勾股数;若是大于2的偶数,把它除以2后再平方,然后用这个平方数分别减1,加1,得到两个整数,则与这两个数组成勾股数.根据上面的规律,由12生成的勾股数的“弦数”是 .
14.(2023八上·沙坪坝期中)如图,折叠矩形纸片,使点落在边的点处,为折痕,,.设的长为,用含有的式子表示四边形的面积是 .
三、计算题
15.(2024八下·哈尔滨月考)先化简,再求值:()÷,其中x=1+,y=1﹣.
16.(2024七下·乌鲁木齐期中)(1)计算:;
(2)解方程组:
①;
②.
17.(2024八下·丛台月考)阅读下列材料,然后回答问题:
在进行类似于二次根式的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
(1)请用两种不同的方法化简:;
(2)化简:.
四、解答题
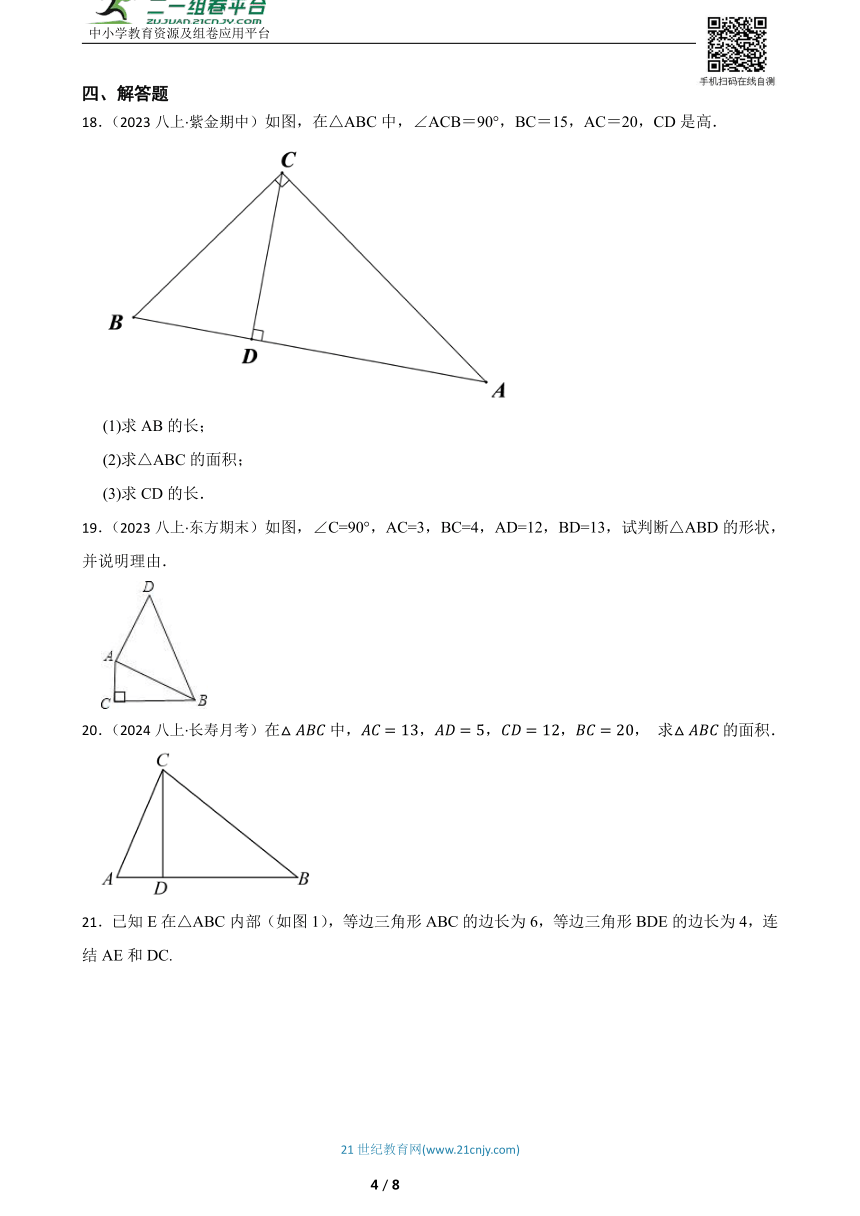
18.(2023八上·紫金期中)如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
19.(2023八上·东方期末)如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.
20.(2024八上·长寿月考)在中,,,,, 求的面积.
21.已知E在△ABC内部(如图1),等边三角形ABC的边长为6,等边三角形BDE的边长为4,连结AE和DC.
(1)求证:AE=DC.
(2)当AE⊥BD时,求CD的长.
(3)将△BDE绕点B旋转一周,F为DC的中点(如图2),求旋转过程中EF的取值范围.
答案解析部分
1.【答案】C
【知识点】三角形的角平分线、中线和高;勾股定理
2.【答案】B
【知识点】二次根式有意义的条件
3.【答案】D
【知识点】线段垂直平分线的性质;等腰三角形的判定与性质;平行四边形的性质
4.【答案】B
【知识点】最简二次根式
5.【答案】C
【知识点】无理数的估值;二次根式的混合运算
6.【答案】D
【知识点】算术平方根;勾股定理的应用
7.【答案】C
【知识点】平行线的性质;勾股定理;三角形的中位线定理
8.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;平行四边形的性质
9.【答案】
【知识点】二次根式的性质与化简;点的坐标与象限的关系;化简含绝对值有理数
10.【答案】
【知识点】二次根式的性质与化简
11.【答案】
【知识点】二次根式有意义的条件
12.【答案】
【知识点】角平分线的性质;等腰三角形的判定与性质;平行四边形的性质
13.【答案】37
【知识点】勾股数
14.【答案】
【知识点】勾股定理
15.【答案】,
【知识点】分式的化简求值;二次根式的混合运算
16.【答案】(1);(2)①;②.
【知识点】二次根式的性质与化简;加减消元法解二元一次方程组;开立方(求立方根)
17.【答案】(1);(2)
【知识点】分母有理化
18.【答案】(1)25;(2)150;(3)12
【知识点】勾股定理
19.【答案】解:△ABD为直角三角形.理由如下:
∵在△ABC中,∠C=90°,
∴AB2=CB2+AC2=42+32=52,
∴在△ABD中,AB2+AD2=52+122=132,
∴AB2+AD2=BD2,
∴△ABD为直角三角形
【知识点】勾股定理;勾股定理的逆定理
20.【答案】
【知识点】勾股定理;勾股定理的逆定理
21.【答案】(1)证明:如图1中,
∵△ABC,△BDE 都是等边三角形,
∴ BA=BC,BE=BD,∠ABC=∠EBD=60°,
∴ ∠ABE=∠CBD,
∴ △ABE≌△CBD (SAS),
∴AE=CD;
(2)解:延长AE交BD于点J.
∵EJ⊥BD,EB=ED,
∴ BJ= JD=2,
∴,
由(1)可知CD=AE,
.
(3)解:延长DE到P,使得EP=DE=4,连接BP、CP,
∵PE=DE,DF=CF,
∴EF是△CDP的中位线,
∴EF=PC,
∵BE=DE=PE,
∴∠EPB=∠EBP,∠EBD=∠EDB,
∴∠PBD=∠PBE+∠DBE=90°,
∴,
∵BC=6,
∴
∴.
【知识点】等边三角形的性质;勾股定理;三角形全等的判定-SAS;三角形的中位线定理
21世纪教育网(www.21cnjy.com)
1 / 8
人教版数学八年级下册期中复习题二【精华】
一、单选题
1.(2024八下·石泉期中)如图,的顶点A,B,C在边长为1的正方形网格的格点上, 于点D,则线段的长为( )
A.4 B. C. D.5
2.(2024七下·江门期中)下列各式中,没有意义的是( )
A. B. C. D.
3.(2024八下·岳阳期末)如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,交AB于点F,P是EB延长线上一点,下列结论:
①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.
其中正确结论的个数为( )
A.1 B.2 C.3 D.4
4.(2024八下·江阳期中)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
5.(2023九下·广阳月考)估计的值应在( )
A.和之间 B.和之间 C.和之间 D.和之间
6.(2022八下·兴仁月考)一旗杆在其的处折断,量得米,则旗杆原来的高度为( )
A.米 B.米 C.10米 D.米
7.(2024八下·镇海区期末)如图,在中,,于点,点在上,,若点分别为的中点,连结,,,则的长为( )
A. B. C. D.
8.(2023八下·万源月考)△ABC中,点D,G分别在边AB,AC上,点E,F在边BC上.已知DG∥BC,DE∥FG,BE=DE,CF=FG,则∠A的度数( )
A.等于90° B.等于80°
C.等于72° D.条件不足,无法计算
二、填空题
9.(2023九上·叙州期中)已知点在第四象限,化简的结果为 .
10.(2024八下·杭州月考) (化成最简二次根式).
11.(2024八下·昌邑期末)若式子在实数范围内有意义,则的取值范围是 .
12.(2024八下·永春期中)如图,在平行四边形中,平分,交于点,平分,交于点,,,则的长为 .
13.(2024八上·盐城月考)《九章算术》提供了许多勾股数如,等,其中一组勾股数中最大的数称为“弦数”.经研究,若是大于1的奇数,把它平方后拆成相邻的两个整数,则与这两个数组成勾股数;若是大于2的偶数,把它除以2后再平方,然后用这个平方数分别减1,加1,得到两个整数,则与这两个数组成勾股数.根据上面的规律,由12生成的勾股数的“弦数”是 .
14.(2023八上·沙坪坝期中)如图,折叠矩形纸片,使点落在边的点处,为折痕,,.设的长为,用含有的式子表示四边形的面积是 .
三、计算题
15.(2024八下·哈尔滨月考)先化简,再求值:()÷,其中x=1+,y=1﹣.
16.(2024七下·乌鲁木齐期中)(1)计算:;
(2)解方程组:
①;
②.
17.(2024八下·丛台月考)阅读下列材料,然后回答问题:
在进行类似于二次根式的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
(1)请用两种不同的方法化简:;
(2)化简:.
四、解答题
18.(2023八上·紫金期中)如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
19.(2023八上·东方期末)如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.
20.(2024八上·长寿月考)在中,,,,, 求的面积.
21.已知E在△ABC内部(如图1),等边三角形ABC的边长为6,等边三角形BDE的边长为4,连结AE和DC.
(1)求证:AE=DC.
(2)当AE⊥BD时,求CD的长.
(3)将△BDE绕点B旋转一周,F为DC的中点(如图2),求旋转过程中EF的取值范围.
答案解析部分
1.【答案】C
【知识点】三角形的角平分线、中线和高;勾股定理
2.【答案】B
【知识点】二次根式有意义的条件
3.【答案】D
【知识点】线段垂直平分线的性质;等腰三角形的判定与性质;平行四边形的性质
4.【答案】B
【知识点】最简二次根式
5.【答案】C
【知识点】无理数的估值;二次根式的混合运算
6.【答案】D
【知识点】算术平方根;勾股定理的应用
7.【答案】C
【知识点】平行线的性质;勾股定理;三角形的中位线定理
8.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;平行四边形的性质
9.【答案】
【知识点】二次根式的性质与化简;点的坐标与象限的关系;化简含绝对值有理数
10.【答案】
【知识点】二次根式的性质与化简
11.【答案】
【知识点】二次根式有意义的条件
12.【答案】
【知识点】角平分线的性质;等腰三角形的判定与性质;平行四边形的性质
13.【答案】37
【知识点】勾股数
14.【答案】
【知识点】勾股定理
15.【答案】,
【知识点】分式的化简求值;二次根式的混合运算
16.【答案】(1);(2)①;②.
【知识点】二次根式的性质与化简;加减消元法解二元一次方程组;开立方(求立方根)
17.【答案】(1);(2)
【知识点】分母有理化
18.【答案】(1)25;(2)150;(3)12
【知识点】勾股定理
19.【答案】解:△ABD为直角三角形.理由如下:
∵在△ABC中,∠C=90°,
∴AB2=CB2+AC2=42+32=52,
∴在△ABD中,AB2+AD2=52+122=132,
∴AB2+AD2=BD2,
∴△ABD为直角三角形
【知识点】勾股定理;勾股定理的逆定理
20.【答案】
【知识点】勾股定理;勾股定理的逆定理
21.【答案】(1)证明:如图1中,
∵△ABC,△BDE 都是等边三角形,
∴ BA=BC,BE=BD,∠ABC=∠EBD=60°,
∴ ∠ABE=∠CBD,
∴ △ABE≌△CBD (SAS),
∴AE=CD;
(2)解:延长AE交BD于点J.
∵EJ⊥BD,EB=ED,
∴ BJ= JD=2,
∴,
由(1)可知CD=AE,
.
(3)解:延长DE到P,使得EP=DE=4,连接BP、CP,
∵PE=DE,DF=CF,
∴EF是△CDP的中位线,
∴EF=PC,
∵BE=DE=PE,
∴∠EPB=∠EBP,∠EBD=∠EDB,
∴∠PBD=∠PBE+∠DBE=90°,
∴,
∵BC=6,
∴
∴.
【知识点】等边三角形的性质;勾股定理;三角形全等的判定-SAS;三角形的中位线定理
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
