人教版数学八年级下册期中复习题三【精华】(含答案)
文档属性
| 名称 | 人教版数学八年级下册期中复习题三【精华】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 05:03:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册期中复习题三【精华】
一、单选题
1.(2024八下·平果期中)如图,在矩形中,,.折叠该矩形,使点B与点D重合,点A落在点G处,则的长为( )
A. B. C. D.3
2.(2023八下·石阡月考)以下列数组为三角形的边长:(1)5,12,13;(2)10,12,13;(3)7,24,25;(4)6,8,10,其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
3.(2022九下·九龙坡模拟)估计的值应在( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
4.(2024八下·湖里月考)在Rt△ABC中,∠C=90°,若AC=5,BC=12,则AB的长为( )
A.5 B.12 C.13 D.15
5.(2024八上·淮阳期末)下列命题中假命题是( )
A.有一个内角等于的等腰三角形是等边三角形
B.等腰三角形的两边长是4和8,则其周长为20
C.同一平面内,过直线外一点有且只有一条直线与这条直线平行
D.直角三角形的三条边长的比可能是
6.(2022·梓潼模拟)如图,四边形ABCD中,则BD的长为( )
A. B. C. D.
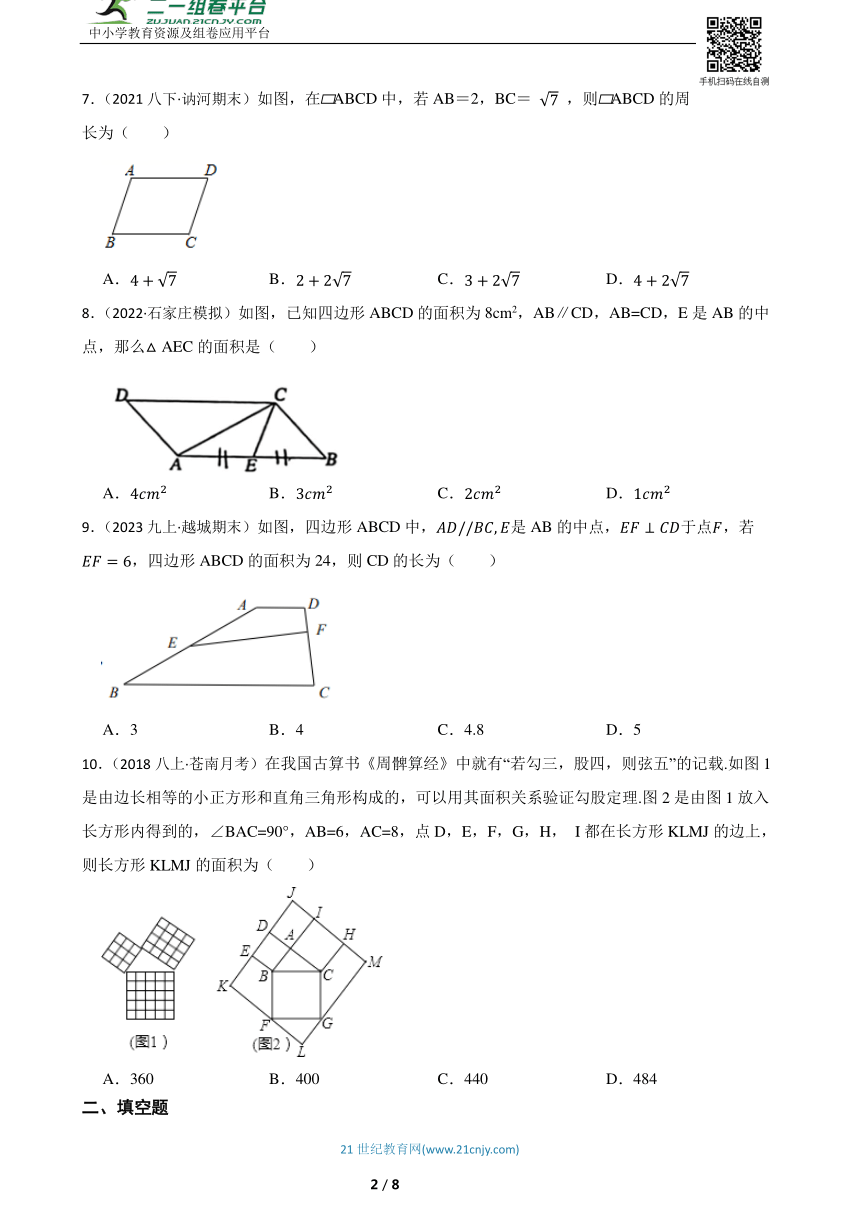
7.(2021八下·讷河期末)如图,在 ABCD中,若AB=2,BC= ,则 ABCD的周长为( )
A. B. C. D.
8.(2022·石家庄模拟)如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A. B. C. D.
9.(2023九上·越城期末)如图,四边形ABCD中,是AB的中点,于点,若,四边形ABCD的面积为24,则CD的长为( )
A.3 B.4 C.4.8 D.5
10.(2018八上·苍南月考)在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,AC=8,点D,E,F,G,H, I都在长方形KLMJ的边上,则长方形KLMJ的面积为( )
A.360 B.400 C.440 D.484
二、填空题
11.(2024九下·龙口模拟)式子在实数范围内有意义,则的取值范围是 .
12.(2024七下·离石期中)去绝对值: .
13.(2024八上·成都期中)如图,在平面直角坐标系中,将绕点A按顺时针方向旋转到的位置,点B、O分别落在点、处,点在x轴上.再将绕点按顺时针方向旋转到的位置,点在x轴上.将绕点按顺时针方向旋转到的位置,点在x轴上,依次进行下去……若点,,则点的横坐标为 .
14.(2023八上·晋州期末)如图所示,图中所有的三角形都是等边三角形.若其中最小的等边三角形的边长为,则图中涂有阴影的等边三角形的边长为 ,周长为 ,面积为 .
15.(2023八下·大名开学考)已知最简二次根式与二次根式可以合并,则的值为 .
16.(2018八上·衢州月考)如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是 .
三、计算题
17.(2024八下·东城期中)计算:
(1);
(2)
18.(2024八上·青浦期末)计算:
19.(2024八上·永修月考)如图,C为线段上一动点,分别过点B,D作,连接.已知.
(1)求当x等于何值时,
(2)当时,求的长.
(3)利用图形求代数式的最小值.
四、解答题
20.(2024八上·丰城期中)已知.
(1)求代数式的值;
(2)求代数式﹣的值.
21.(2023八下·息县期末)如图,在中,于点,.
(1)求和的长;
(2)求的度数.
22.(2024八上·甘州期中)如图,小区有一块三角形空地,为响应张掖市创建全国文明典范城市的号召,小区计划将这块空地种上三种不同的花卉,中间用小路、隔开,.经测量,米,米,米,米.
(1)求的长;
(2)求小路的长.
23.已知a,b,c为正数,满足如下两个条件:
a+b+c=32 ①
②
是否存在以 , , 为三边长的三角形?如果存在,求出三角形的最大内角.
答案解析部分
1.【答案】A
【知识点】勾股定理
2.【答案】B
【知识点】勾股定理的逆定理
3.【答案】C
【知识点】无理数的估值;二次根式的乘除法
4.【答案】C
【知识点】勾股定理
5.【答案】D
【知识点】等边三角形的判定;勾股定理的逆定理;真命题与假命题;等腰三角形的概念
6.【答案】C
【知识点】平行线之间的距离;三角形的面积;等腰三角形的性质;勾股定理
7.【答案】D
【知识点】平行四边形的性质
8.【答案】C
【知识点】三角形的面积;平行四边形的判定与性质
9.【答案】B
【知识点】平行四边形的判定与性质;三角形全等的判定-AAS
10.【答案】C
【知识点】勾股定理的证明
11.【答案】且
【知识点】分式有无意义的条件;二次根式有意义的条件
12.【答案】
【知识点】二次根式的加减法;求有理数的绝对值的方法
13.【答案】10126
【知识点】点的坐标;勾股定理
14.【答案】4;12;
【知识点】等边三角形的性质;勾股定理
15.【答案】2
【知识点】最简二次根式;同类二次根式
16.【答案】 或5或8
【知识点】等腰三角形的性质;勾股定理
17.【答案】(1)
(2)
【知识点】二次根式的混合运算
18.【答案】解:原式=
=
= .
【知识点】二次根式的性质与化简;二次根式的化简求值
19.【答案】(1)
(2)
(3)
【知识点】勾股定理
20.【答案】(1)(2)1
【知识点】分式的化简求值;二次根式有意义的条件;二次根式的性质与化简
21.【答案】(1);
(2)
【知识点】勾股定理;勾股定理的逆定理
22.【答案】(1)米
(2)米
【知识点】三角形的面积;勾股定理;勾股定理的逆定理;邻补角
23.【答案】解:解法1:将①②两式相乘,得 ,即: ,即 ,即 ,即 ,即 ,即 ,即 ,即 ,所以b﹣c+a=0或c+a﹣b=0或c﹣a+b=0,即b+a=c或c+a=b或c+b=a.因此,以 , , 为三边长可构成一个直角三角形,它的最大内角为90°.解法2:结合①式,由②式可得 ,变形,得 ③又由①式得(a+b+c)2=1024,即a2+b2+c2=1024﹣2(ab+bc+ca),代入③式,得 ,即abc=16(ab+bc+ca)﹣4096.(a﹣16)(b﹣16)(c﹣16)=abc﹣16(ab+bc+ca)+256(a+b+c)﹣163=﹣4096+256×32﹣163=0,所以a=16或b=16或c=16.结合①式可得b+a=c或c+a=b或c+b=a.因此,以 , , 为三边长可构成一个直角三角形,它的最大内角为90°
【知识点】勾股定理的逆定理
21世纪教育网(www.21cnjy.com)
1 / 8
人教版数学八年级下册期中复习题三【精华】
一、单选题
1.(2024八下·平果期中)如图,在矩形中,,.折叠该矩形,使点B与点D重合,点A落在点G处,则的长为( )
A. B. C. D.3
2.(2023八下·石阡月考)以下列数组为三角形的边长:(1)5,12,13;(2)10,12,13;(3)7,24,25;(4)6,8,10,其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
3.(2022九下·九龙坡模拟)估计的值应在( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
4.(2024八下·湖里月考)在Rt△ABC中,∠C=90°,若AC=5,BC=12,则AB的长为( )
A.5 B.12 C.13 D.15
5.(2024八上·淮阳期末)下列命题中假命题是( )
A.有一个内角等于的等腰三角形是等边三角形
B.等腰三角形的两边长是4和8,则其周长为20
C.同一平面内,过直线外一点有且只有一条直线与这条直线平行
D.直角三角形的三条边长的比可能是
6.(2022·梓潼模拟)如图,四边形ABCD中,则BD的长为( )
A. B. C. D.
7.(2021八下·讷河期末)如图,在 ABCD中,若AB=2,BC= ,则 ABCD的周长为( )
A. B. C. D.
8.(2022·石家庄模拟)如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A. B. C. D.
9.(2023九上·越城期末)如图,四边形ABCD中,是AB的中点,于点,若,四边形ABCD的面积为24,则CD的长为( )
A.3 B.4 C.4.8 D.5
10.(2018八上·苍南月考)在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,AC=8,点D,E,F,G,H, I都在长方形KLMJ的边上,则长方形KLMJ的面积为( )
A.360 B.400 C.440 D.484
二、填空题
11.(2024九下·龙口模拟)式子在实数范围内有意义,则的取值范围是 .
12.(2024七下·离石期中)去绝对值: .
13.(2024八上·成都期中)如图,在平面直角坐标系中,将绕点A按顺时针方向旋转到的位置,点B、O分别落在点、处,点在x轴上.再将绕点按顺时针方向旋转到的位置,点在x轴上.将绕点按顺时针方向旋转到的位置,点在x轴上,依次进行下去……若点,,则点的横坐标为 .
14.(2023八上·晋州期末)如图所示,图中所有的三角形都是等边三角形.若其中最小的等边三角形的边长为,则图中涂有阴影的等边三角形的边长为 ,周长为 ,面积为 .
15.(2023八下·大名开学考)已知最简二次根式与二次根式可以合并,则的值为 .
16.(2018八上·衢州月考)如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是 .
三、计算题
17.(2024八下·东城期中)计算:
(1);
(2)
18.(2024八上·青浦期末)计算:
19.(2024八上·永修月考)如图,C为线段上一动点,分别过点B,D作,连接.已知.
(1)求当x等于何值时,
(2)当时,求的长.
(3)利用图形求代数式的最小值.
四、解答题
20.(2024八上·丰城期中)已知.
(1)求代数式的值;
(2)求代数式﹣的值.
21.(2023八下·息县期末)如图,在中,于点,.
(1)求和的长;
(2)求的度数.
22.(2024八上·甘州期中)如图,小区有一块三角形空地,为响应张掖市创建全国文明典范城市的号召,小区计划将这块空地种上三种不同的花卉,中间用小路、隔开,.经测量,米,米,米,米.
(1)求的长;
(2)求小路的长.
23.已知a,b,c为正数,满足如下两个条件:
a+b+c=32 ①
②
是否存在以 , , 为三边长的三角形?如果存在,求出三角形的最大内角.
答案解析部分
1.【答案】A
【知识点】勾股定理
2.【答案】B
【知识点】勾股定理的逆定理
3.【答案】C
【知识点】无理数的估值;二次根式的乘除法
4.【答案】C
【知识点】勾股定理
5.【答案】D
【知识点】等边三角形的判定;勾股定理的逆定理;真命题与假命题;等腰三角形的概念
6.【答案】C
【知识点】平行线之间的距离;三角形的面积;等腰三角形的性质;勾股定理
7.【答案】D
【知识点】平行四边形的性质
8.【答案】C
【知识点】三角形的面积;平行四边形的判定与性质
9.【答案】B
【知识点】平行四边形的判定与性质;三角形全等的判定-AAS
10.【答案】C
【知识点】勾股定理的证明
11.【答案】且
【知识点】分式有无意义的条件;二次根式有意义的条件
12.【答案】
【知识点】二次根式的加减法;求有理数的绝对值的方法
13.【答案】10126
【知识点】点的坐标;勾股定理
14.【答案】4;12;
【知识点】等边三角形的性质;勾股定理
15.【答案】2
【知识点】最简二次根式;同类二次根式
16.【答案】 或5或8
【知识点】等腰三角形的性质;勾股定理
17.【答案】(1)
(2)
【知识点】二次根式的混合运算
18.【答案】解:原式=
=
= .
【知识点】二次根式的性质与化简;二次根式的化简求值
19.【答案】(1)
(2)
(3)
【知识点】勾股定理
20.【答案】(1)(2)1
【知识点】分式的化简求值;二次根式有意义的条件;二次根式的性质与化简
21.【答案】(1);
(2)
【知识点】勾股定理;勾股定理的逆定理
22.【答案】(1)米
(2)米
【知识点】三角形的面积;勾股定理;勾股定理的逆定理;邻补角
23.【答案】解:解法1:将①②两式相乘,得 ,即: ,即 ,即 ,即 ,即 ,即 ,即 ,即 ,所以b﹣c+a=0或c+a﹣b=0或c﹣a+b=0,即b+a=c或c+a=b或c+b=a.因此,以 , , 为三边长可构成一个直角三角形,它的最大内角为90°.解法2:结合①式,由②式可得 ,变形,得 ③又由①式得(a+b+c)2=1024,即a2+b2+c2=1024﹣2(ab+bc+ca),代入③式,得 ,即abc=16(ab+bc+ca)﹣4096.(a﹣16)(b﹣16)(c﹣16)=abc﹣16(ab+bc+ca)+256(a+b+c)﹣163=﹣4096+256×32﹣163=0,所以a=16或b=16或c=16.结合①式可得b+a=c或c+a=b或c+b=a.因此,以 , , 为三边长可构成一个直角三角形,它的最大内角为90°
【知识点】勾股定理的逆定理
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
