8.1.2 第1课时 幂的乘方 课件(共21张PPT)——沪科版(2024)七年级数学下册
文档属性
| 名称 | 8.1.2 第1课时 幂的乘方 课件(共21张PPT)——沪科版(2024)七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 540.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 09:13:29 | ||
图片预览








文档简介
(共21张PPT)
8.1.2 幂的乘方与积的乘方
第一课时 幂的乘方
学习目标及重难点
1.理解并掌握幂的乘方法则;(重点)
2.掌握幂的乘方法则的推导过程并能灵活运用.(难点)
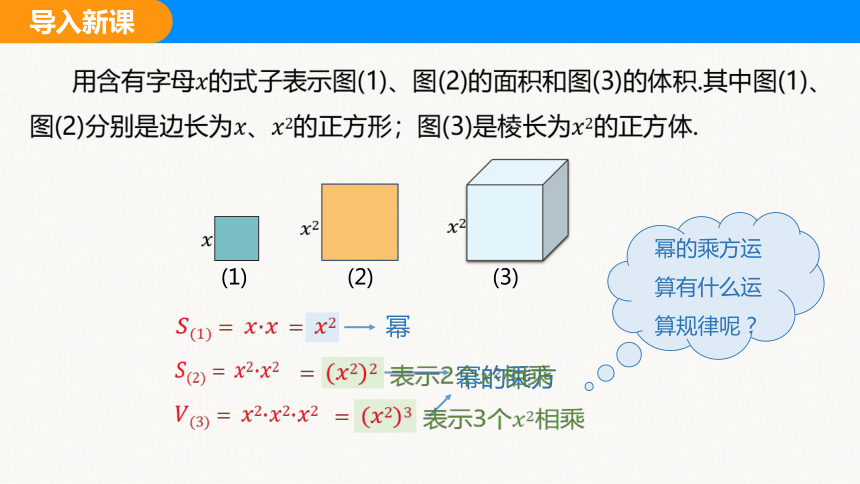
用含有字母的式子表示图(1)、图(2)的面积和图(3)的体积.其中图(1)、图(2)分别是边长为的正方形;图(3)是棱长为的正方体.
(1)
(2)
(3)
幂
幂的乘方
表示2个相乘
表示3个相乘
幂的乘方运算有什么运算规律呢?
探索1:幂的乘方
思考:怎样计算
算 式 运算过程 结 果
1.先完成下表:
算 式 运算过程 结 果
2.观察这个表,发现幂的乘方有什么规律?
1.结果的底数与原来的底数相同;
2.结果的指数等于原来两个指数的积.
算 式 运算过程 结 果
2.观察这个表,发现幂的乘方有什么规律?
猜想: = (都是正整数)
3.你能验证刚刚的猜想吗?
小组合作
1.独立思考,完成验证;
2.两人一组,交流思路,完善过程.
猜想:=
(都是正整数)
3.你能验证刚刚的猜想吗?
一般地,如果 都是正整数,那么
个
个
同底数幂的乘法法则
乘方的意义
猜想:=
(都是正整数)
幂的运算性质2:
(都是正整数).
幂的乘方,底数不变,指数相乘.
归纳总结
例1:计算
(1); (2).
解:(1)
(2)
计算的结果是( )
A. B.
C. D.
B
随堂小练习
运算 种类 公式 法则 中运算 计算结果 底数 指数
同底数幂的乘法
幂的乘方
乘法
乘方
不变
不变
指数
相加
指数
相乘
比一比
幂的运算性质1与幂的运算性质2有什么相同点和不同点?
随堂小练习
下列计算正确的是( )
A. B.
C. D.
D
分析:按有理数混合运算的运算顺序计算,先乘方,后乘除,最后加减,有括号的先算括号里的.
例2:(1); (2)
解:(1)=;
(2)=
例3:若则等于( )
A. 7 B. 12
C. 432 D. 108
C
分析:根据同底数幂的乘方运算性质的逆用和幂的乘方的性质计算即可.
1.下列计算结果是的是( ).
A. B. C. D.
D
习题1
习题2
2.如果正方体的棱长为,那么这个正方体的表面积为( )
A. B.
C. D.
B
3.计算:
(1) ; (2) ;
(3) (4) ;
解: (1) ;
(2) = ;
(3) =;
(4) =;
习题3
4.已知求的值.
解:
=
=
习题4
阅读下列解题过程:
试比较2100与375的大小.
解:因为2100=(24)25=1625,375=(33)25=2725,且16<27,所以2100<375.
试根据上述解答过程解决问题:比较2555,3444,4333的大小.
拓展提升
解:因为2555=(25)111=32111,3444=(34)111=81111,4333=(43)111=64111,且32<64<81,所以2555<4333<3444.
幂的乘方
法则
注意
(am)n=amn (m,n都是正整数)
幂的乘方,底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别(am)n=amn; am﹒an=am+n
幂的乘方法则的逆用amn=(am)n=(an)m
8.1.2 幂的乘方与积的乘方
第一课时 幂的乘方
学习目标及重难点
1.理解并掌握幂的乘方法则;(重点)
2.掌握幂的乘方法则的推导过程并能灵活运用.(难点)
用含有字母的式子表示图(1)、图(2)的面积和图(3)的体积.其中图(1)、图(2)分别是边长为的正方形;图(3)是棱长为的正方体.
(1)
(2)
(3)
幂
幂的乘方
表示2个相乘
表示3个相乘
幂的乘方运算有什么运算规律呢?
探索1:幂的乘方
思考:怎样计算
算 式 运算过程 结 果
1.先完成下表:
算 式 运算过程 结 果
2.观察这个表,发现幂的乘方有什么规律?
1.结果的底数与原来的底数相同;
2.结果的指数等于原来两个指数的积.
算 式 运算过程 结 果
2.观察这个表,发现幂的乘方有什么规律?
猜想: = (都是正整数)
3.你能验证刚刚的猜想吗?
小组合作
1.独立思考,完成验证;
2.两人一组,交流思路,完善过程.
猜想:=
(都是正整数)
3.你能验证刚刚的猜想吗?
一般地,如果 都是正整数,那么
个
个
同底数幂的乘法法则
乘方的意义
猜想:=
(都是正整数)
幂的运算性质2:
(都是正整数).
幂的乘方,底数不变,指数相乘.
归纳总结
例1:计算
(1); (2).
解:(1)
(2)
计算的结果是( )
A. B.
C. D.
B
随堂小练习
运算 种类 公式 法则 中运算 计算结果 底数 指数
同底数幂的乘法
幂的乘方
乘法
乘方
不变
不变
指数
相加
指数
相乘
比一比
幂的运算性质1与幂的运算性质2有什么相同点和不同点?
随堂小练习
下列计算正确的是( )
A. B.
C. D.
D
分析:按有理数混合运算的运算顺序计算,先乘方,后乘除,最后加减,有括号的先算括号里的.
例2:(1); (2)
解:(1)=;
(2)=
例3:若则等于( )
A. 7 B. 12
C. 432 D. 108
C
分析:根据同底数幂的乘方运算性质的逆用和幂的乘方的性质计算即可.
1.下列计算结果是的是( ).
A. B. C. D.
D
习题1
习题2
2.如果正方体的棱长为,那么这个正方体的表面积为( )
A. B.
C. D.
B
3.计算:
(1) ; (2) ;
(3) (4) ;
解: (1) ;
(2) = ;
(3) =;
(4) =;
习题3
4.已知求的值.
解:
=
=
习题4
阅读下列解题过程:
试比较2100与375的大小.
解:因为2100=(24)25=1625,375=(33)25=2725,且16<27,所以2100<375.
试根据上述解答过程解决问题:比较2555,3444,4333的大小.
拓展提升
解:因为2555=(25)111=32111,3444=(34)111=81111,4333=(43)111=64111,且32<64<81,所以2555<4333<3444.
幂的乘方
法则
注意
(am)n=amn (m,n都是正整数)
幂的乘方,底数不变,指数相乘
幂的乘方与同底数幂的乘法的区别(am)n=amn; am﹒an=am+n
幂的乘方法则的逆用amn=(am)n=(an)m
