8.2.3 多项式与多项式相乘 课件(共27张PPT)——沪科版(2024)七年级数学下册
文档属性
| 名称 | 8.2.3 多项式与多项式相乘 课件(共27张PPT)——沪科版(2024)七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 660.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
8.2.3 多项式与多项式相乘
学习目标及重难点
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.
(难点)
单项式乘法法则:
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
如:
单项式乘多项式的法则:
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
如:
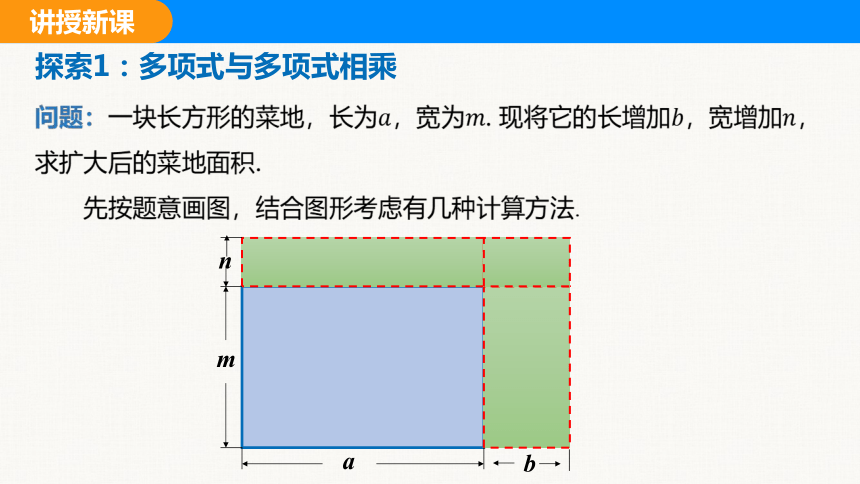
探索1:多项式与多项式相乘
问题:一块长方形的菜地,长为,宽为. 现将它的长增加,宽增加,求扩大后的菜地面积.
先按题意画图,结合图形考虑有几种计算方法.
m
a
n
b
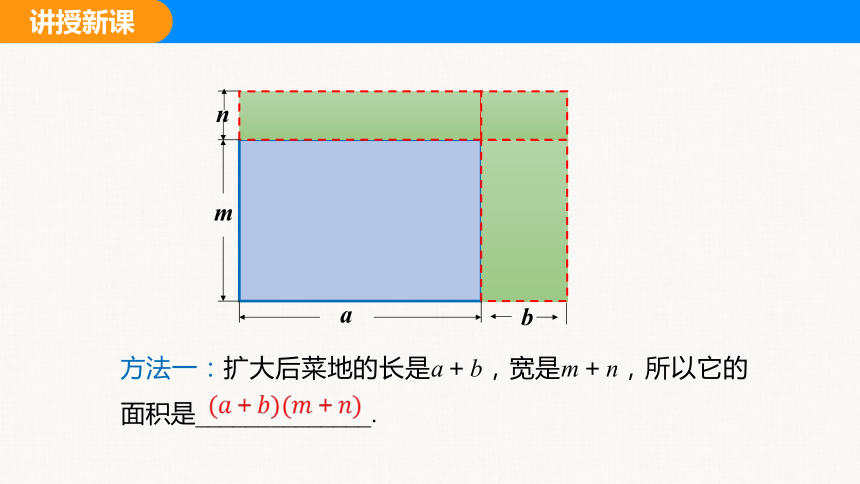
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是______________.
m
a
n
b
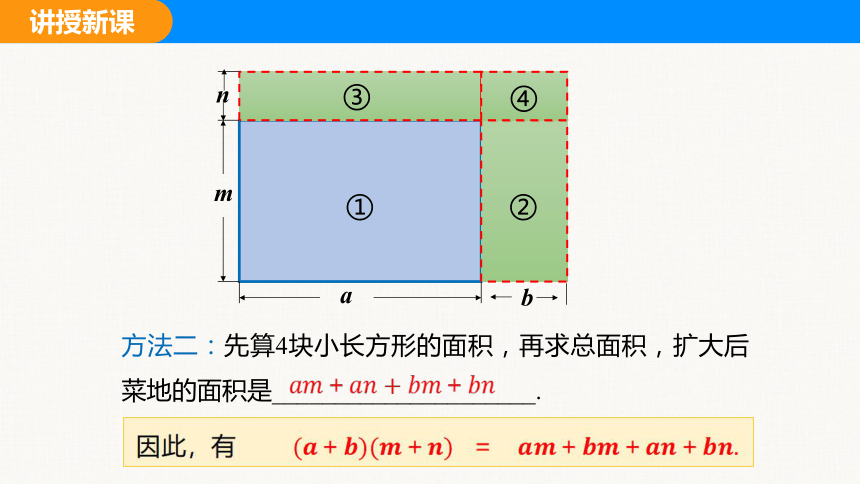
方法二:先算4块小长方形的面积,再求总面积,扩大后菜地的面积是_____________________.
因此,有
m
a
n
b
①
②
③
④
上面的运算还可以把看作一个整体运用分配律,再根据单项式与多项式的乘法法则,得
=
=
单项式(整体)×多项式
单项式×多项式
因此,有
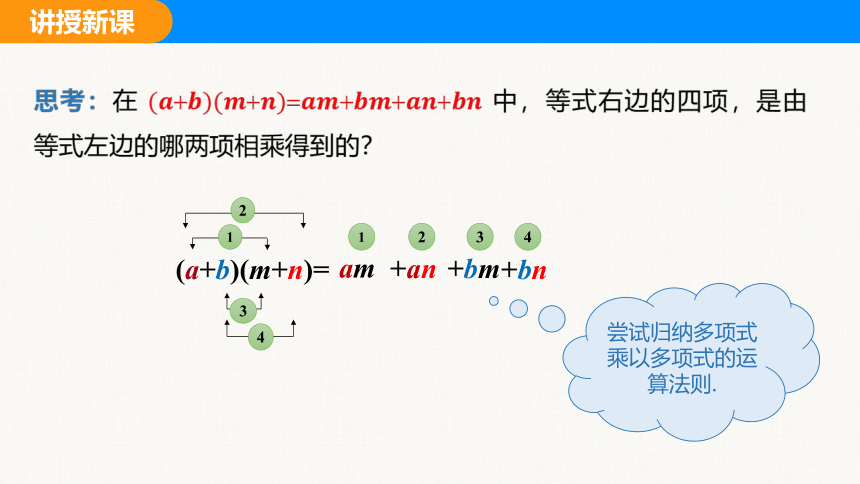
思考:在 中,等式右边的四项,是由等式左边的哪两项相乘得到的?
2
3
4
(a+b)(m+n)=
am
1
2
3
4
+bm
+an
+bn
1
尝试归纳多项式乘以多项式的运算法则.
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加 .
单项式×
多项式
单项式×
单项式
多项式×
多项式
多项式乘多项式的乘法法则:
归纳总结
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
多乘多顺口溜:
归纳总结
2
3
4
(a+b)(m+n)=
am
1
2
3
4
+bm
+an
+bn
1
例1:计算:
(1); (2).
解:(1)
=
=
=
例1:计算:
(1); (2).
解:(2)
=
=
随堂小练习
1. 计算的结果为( )
A. B.
C. D.
B
随堂小练习
2.
= ——乘法对加法的分配律
=——单项式乘多项式法则
=. ——合并同类项
例2:计算:
(1); (2).
解:(1)
=
=
例2:计算:
(1); (2).
解:(2)
=
=
随堂小练习
计算:
(1) ; (2)
解:(1)
=
=
(2)
=
=
例3:先化简,再求值:其中.
解:原式=
=
=
当时,原式
随堂小练习
先化简,再求值:
,其中;
解:原式=.
当时,
原式=
1.若,则 ( )
A. B.
C. D.
C
习题1
习题2
2.已知M,N分别是2次多项式和3次多项式,则M×N=( )
A.一定是5次多项式
B.一定是6次多项式
C.一定是不高于5次的多项式
D.无法确定积的次数
A
习题3
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
5 6
(-3) (-4)
2 (-8)
(-5) 6
口答:
3.计算:
习题4
4.计算:(1) ; (2) ;
解:(1)
(2)
5.先化简,再求值:
其中.
解:原式=
=
=
当时,
原式=
习题5
多项式展开后不含的一次项,求的值.
解:
原式=
+
8·2
+
+
=
=
=
因为多项式展开后不含x的一次项.
所以
所以
拓展提升
多项式
×
多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
注意
(a+b)(m+n)=am+an+bm+bn
不要漏乘;正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
(x-1)2=(x-1)(x-1),而不是x2-12.
8.2.3 多项式与多项式相乘
学习目标及重难点
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.
(难点)
单项式乘法法则:
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
如:
单项式乘多项式的法则:
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
如:
探索1:多项式与多项式相乘
问题:一块长方形的菜地,长为,宽为. 现将它的长增加,宽增加,求扩大后的菜地面积.
先按题意画图,结合图形考虑有几种计算方法.
m
a
n
b
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是______________.
m
a
n
b
方法二:先算4块小长方形的面积,再求总面积,扩大后菜地的面积是_____________________.
因此,有
m
a
n
b
①
②
③
④
上面的运算还可以把看作一个整体运用分配律,再根据单项式与多项式的乘法法则,得
=
=
单项式(整体)×多项式
单项式×多项式
因此,有
思考:在 中,等式右边的四项,是由等式左边的哪两项相乘得到的?
2
3
4
(a+b)(m+n)=
am
1
2
3
4
+bm
+an
+bn
1
尝试归纳多项式乘以多项式的运算法则.
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加 .
单项式×
多项式
单项式×
单项式
多项式×
多项式
多项式乘多项式的乘法法则:
归纳总结
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
多乘多顺口溜:
归纳总结
2
3
4
(a+b)(m+n)=
am
1
2
3
4
+bm
+an
+bn
1
例1:计算:
(1); (2).
解:(1)
=
=
=
例1:计算:
(1); (2).
解:(2)
=
=
随堂小练习
1. 计算的结果为( )
A. B.
C. D.
B
随堂小练习
2.
= ——乘法对加法的分配律
=——单项式乘多项式法则
=. ——合并同类项
例2:计算:
(1); (2).
解:(1)
=
=
例2:计算:
(1); (2).
解:(2)
=
=
随堂小练习
计算:
(1) ; (2)
解:(1)
=
=
(2)
=
=
例3:先化简,再求值:其中.
解:原式=
=
=
当时,原式
随堂小练习
先化简,再求值:
,其中;
解:原式=.
当时,
原式=
1.若,则 ( )
A. B.
C. D.
C
习题1
习题2
2.已知M,N分别是2次多项式和3次多项式,则M×N=( )
A.一定是5次多项式
B.一定是6次多项式
C.一定是不高于5次的多项式
D.无法确定积的次数
A
习题3
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
5 6
(-3) (-4)
2 (-8)
(-5) 6
口答:
3.计算:
习题4
4.计算:(1) ; (2) ;
解:(1)
(2)
5.先化简,再求值:
其中.
解:原式=
=
=
当时,
原式=
习题5
多项式展开后不含的一次项,求的值.
解:
原式=
+
8·2
+
+
=
=
=
因为多项式展开后不含x的一次项.
所以
所以
拓展提升
多项式
×
多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
注意
(a+b)(m+n)=am+an+bm+bn
不要漏乘;正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
(x-1)2=(x-1)(x-1),而不是x2-12.
