8.3.1 完全平方公式 课件(共33张PPT)——沪科版(2024)七年级数学下册
文档属性
| 名称 | 8.3.1 完全平方公式 课件(共33张PPT)——沪科版(2024)七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 928.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 09:22:25 | ||
图片预览











文档简介
(共33张PPT)
8.3 完全平方公式与平方差公式
第一课时 完全平方公式
学习目标及重难点
1.完全平方公式的推导及应用.(重点)
2.掌握完全平方公式的结构特征及应用.(难点)
先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘
多项式与多项式的乘法法则
复习回顾
探究1:计算下列多项式的积,看谁算得又快又对?
;
探索1:完全平方公式的认识
问题1:观察上面的等式,原算式有什么共同点?
均为两个数的和的平方.
探究1:计算下列多项式的积,看谁算得又快又对?
;
问题2:原算式中的各项与它们结果中的各项有什么关系?
两个数的和的平方,恰好是这两个数的平方和,加上这两个数的积的2倍.
探究1:计算下列多项式的积,看谁算得又快又对?
;
问题3:能否将发现的规律用式子表示出来?
猜想:
思考:你能对发现的规律进行推导吗?
小组合作
1.独立思考,完成验证;
2.两人一组,交流思路,完善过程.
思考:你能对发现的规律进行推导吗?
多项式乘法法则
合并同类项
完全平方公式:
.
两个数的和的平方,等于这两个数的平方和加上这两个数乘积的2倍.
探究2:能类比两数和的完全平方公式的推导过程,表示两数差的完全平方吗?即:
法一:
法二:
完全平方公式:
两个数的差的平方,等于这两个数的平方和减这两个数乘积的2倍.
符号语言:
文字语言:
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
完全平方公式
公式的特征
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的两倍,且与两数中间的符号相同;
公式中的字母可以表示数、单项式或多项式.
1
2
3
4
简记:
首平方,尾平方,积的2倍中间放.
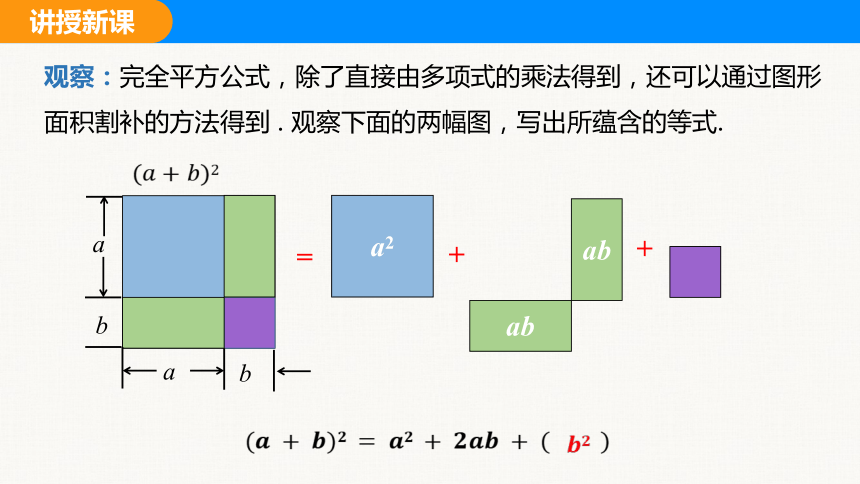
观察:完全平方公式,除了直接由多项式的乘法得到,还可以通过图形面积割补的方法得到 . 观察下面的两幅图,写出所蕴含的等式.
a
b
a
b
a2
ab
ab
=
+
+
观察:完全平方公式,除了直接由多项式的乘法得到,还可以通过图形面积割补的方法得到 . 观察下面的两幅图,写出所蕴含的等式.
a
b
a
b
a2
b2
=
+
例1:利用乘法公式计算:
(1) ; (2)
解:(1) =
运用公式计算,要先识别公式中在具体式子中分别表示什么.
例1:利用乘法公式计算:
(1) ; (2)
解:(2)
例2:利用乘法公式计算:
解:
=
=
=
还有其他计算方法吗?
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)
(2)
(3)
(4)
×
×
×
×
随堂小练习
例3:已知,求的值.
分析:将两数的和(差)的平方式展开,产生两数的平
方和与这两数积的两倍,再将条件代入求解.
解:因为
所以
探索2:完全平方公式的运用
若 求.
解:
随堂小练习
例4:运用完全平方公式进行计算.
(1) 1022
(2) 1972
解:(1)原式=
=
=
=
思考:怎样计
更简便呢?
把和是写成还是,应该怎样确定?
例4:运用完全平方公式进行计算.
(1) 1022
(2) 1972
解:(1)原式=
=
=
=
思考:怎样计
更简便呢?
把和是写成还是,应该怎样确定?
随堂小练习
运用完全平方公式计算:
(1) ; (2) .
解:(1)原式=
=
=
=;
随堂小练习
运用完全平方公式计算:
(1) ; (2) .
(2)原式=
=
=
=.
1.下列计算中,正确的是( D )
A.
B.
C.
D.
D
习题1
解:原式 =
=
=
方法总结:把其中两项看成一个整体,再运用完全平方公式计算.
2.运用乘法公式计算:
习题2
习题3
3.如果是一个完全平方式,求的值.
解:∵
,
∴,
∴,
∴1.
方法总结:两数的平方和加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
习题4
4.利用完全平方公式计算.
(1) 5022
解:原式=
2×500×2
22
+
=250000
+2000
+4
=5002
+
(500+2)2
=252004
(2) 4982
习题4
4.利用完全平方公式计算.
(1) 5022
(2) 4982
解:原式=
2×500×2
22
+
=250000
-2000
+4
=5002
-
(500-2)2
=248004
5.如果把一张正方形的纸片沿着各边都剪去3cm宽的一条,那么所得小正方形的面积比原正方形的面积少了84cm ,求原正方形的边长.
解:设原正方形的边长为cm.则
∴原正方形的边长为cm.
习题5
拓展提升
1.已知求下列各式的值.
(1) ;
(2)
完全平方公式的高频变形
(1);
(2);
(3)
拓展提升
1.已知求下列各式的值.
(1) ;
(2)
解:,
即,①
②
①+ ②得)=60,所以
① ②得x
解:,
,即①;
②;
由①②得③,
②③得.即,故
2.已知求.
拓展提升
完全平方公式
注意
1.项数、符号、字母及其指数
法则
2.不能直接应用公式进行计算的式子,需要先添括号变形
(a±b)2= a2 ±2ab+b2
3.弄清完全平方公式和平方差公式的不同点(从公式结构特点及结果两方面)
8.3 完全平方公式与平方差公式
第一课时 完全平方公式
学习目标及重难点
1.完全平方公式的推导及应用.(重点)
2.掌握完全平方公式的结构特征及应用.(难点)
先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘
多项式与多项式的乘法法则
复习回顾
探究1:计算下列多项式的积,看谁算得又快又对?
;
探索1:完全平方公式的认识
问题1:观察上面的等式,原算式有什么共同点?
均为两个数的和的平方.
探究1:计算下列多项式的积,看谁算得又快又对?
;
问题2:原算式中的各项与它们结果中的各项有什么关系?
两个数的和的平方,恰好是这两个数的平方和,加上这两个数的积的2倍.
探究1:计算下列多项式的积,看谁算得又快又对?
;
问题3:能否将发现的规律用式子表示出来?
猜想:
思考:你能对发现的规律进行推导吗?
小组合作
1.独立思考,完成验证;
2.两人一组,交流思路,完善过程.
思考:你能对发现的规律进行推导吗?
多项式乘法法则
合并同类项
完全平方公式:
.
两个数的和的平方,等于这两个数的平方和加上这两个数乘积的2倍.
探究2:能类比两数和的完全平方公式的推导过程,表示两数差的完全平方吗?即:
法一:
法二:
完全平方公式:
两个数的差的平方,等于这两个数的平方和减这两个数乘积的2倍.
符号语言:
文字语言:
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
完全平方公式
公式的特征
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的两倍,且与两数中间的符号相同;
公式中的字母可以表示数、单项式或多项式.
1
2
3
4
简记:
首平方,尾平方,积的2倍中间放.
观察:完全平方公式,除了直接由多项式的乘法得到,还可以通过图形面积割补的方法得到 . 观察下面的两幅图,写出所蕴含的等式.
a
b
a
b
a2
ab
ab
=
+
+
观察:完全平方公式,除了直接由多项式的乘法得到,还可以通过图形面积割补的方法得到 . 观察下面的两幅图,写出所蕴含的等式.
a
b
a
b
a2
b2
=
+
例1:利用乘法公式计算:
(1) ; (2)
解:(1) =
运用公式计算,要先识别公式中在具体式子中分别表示什么.
例1:利用乘法公式计算:
(1) ; (2)
解:(2)
例2:利用乘法公式计算:
解:
=
=
=
还有其他计算方法吗?
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)
(2)
(3)
(4)
×
×
×
×
随堂小练习
例3:已知,求的值.
分析:将两数的和(差)的平方式展开,产生两数的平
方和与这两数积的两倍,再将条件代入求解.
解:因为
所以
探索2:完全平方公式的运用
若 求.
解:
随堂小练习
例4:运用完全平方公式进行计算.
(1) 1022
(2) 1972
解:(1)原式=
=
=
=
思考:怎样计
更简便呢?
把和是写成还是,应该怎样确定?
例4:运用完全平方公式进行计算.
(1) 1022
(2) 1972
解:(1)原式=
=
=
=
思考:怎样计
更简便呢?
把和是写成还是,应该怎样确定?
随堂小练习
运用完全平方公式计算:
(1) ; (2) .
解:(1)原式=
=
=
=;
随堂小练习
运用完全平方公式计算:
(1) ; (2) .
(2)原式=
=
=
=.
1.下列计算中,正确的是( D )
A.
B.
C.
D.
D
习题1
解:原式 =
=
=
方法总结:把其中两项看成一个整体,再运用完全平方公式计算.
2.运用乘法公式计算:
习题2
习题3
3.如果是一个完全平方式,求的值.
解:∵
,
∴,
∴,
∴1.
方法总结:两数的平方和加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
习题4
4.利用完全平方公式计算.
(1) 5022
解:原式=
2×500×2
22
+
=250000
+2000
+4
=5002
+
(500+2)2
=252004
(2) 4982
习题4
4.利用完全平方公式计算.
(1) 5022
(2) 4982
解:原式=
2×500×2
22
+
=250000
-2000
+4
=5002
-
(500-2)2
=248004
5.如果把一张正方形的纸片沿着各边都剪去3cm宽的一条,那么所得小正方形的面积比原正方形的面积少了84cm ,求原正方形的边长.
解:设原正方形的边长为cm.则
∴原正方形的边长为cm.
习题5
拓展提升
1.已知求下列各式的值.
(1) ;
(2)
完全平方公式的高频变形
(1);
(2);
(3)
拓展提升
1.已知求下列各式的值.
(1) ;
(2)
解:,
即,①
②
①+ ②得)=60,所以
① ②得x
解:,
,即①;
②;
由①②得③,
②③得.即,故
2.已知求.
拓展提升
完全平方公式
注意
1.项数、符号、字母及其指数
法则
2.不能直接应用公式进行计算的式子,需要先添括号变形
(a±b)2= a2 ±2ab+b2
3.弄清完全平方公式和平方差公式的不同点(从公式结构特点及结果两方面)
