8.2.1 单项式与单项式相乘 课件(共23张PPT)——沪科版(2024)七年级数学下册
文档属性
| 名称 | 8.2.1 单项式与单项式相乘 课件(共23张PPT)——沪科版(2024)七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 09:32:03 | ||
图片预览








文档简介
(共23张PPT)
8.2.1 单项式与单项式相乘
学习目标及重难点
1.掌握单项式与单项式相乘的运算法则.(重点)
2.能够灵活地进行单项式与单项式相乘的运算.(难点)
单项式:
多项式:
下列整式中哪些是单项式,哪些是多项式?
a, ,
2
a,
,
探索1:单项式与单项式相乘
问题1:光的速度大约是 km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要约4年才能到达地球,如果1年以 s计算,地球与这颗恒星的距离约为多少千米?
如何计算?
问题1:光的速度大约是 km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要约4年才能到达地球,如果1年以 s计算,地球与这颗恒星的距离约为多少千米?
因而,地球与这颗恒星的距离约为 km.
交流:1. 下面的运算用了哪些性质?
乘法交换律,乘法结合律以及同底数幂的乘法
因而,地球与这颗恒星的距离约为 km.
乘法交换律、结合律
同底数幂的乘法
( ×)×(××)
交流:2.如果把下面算式中的数字换成字母,该如何计算呢
算式:
(单项式与单项式相乘)
=
(乘法交换律和结合律)
=
(同底数幂相乘)
=
交流:3. 完成下面计算:
;
从以上的计算过程中,你能归纳出单项式乘法法则吗?
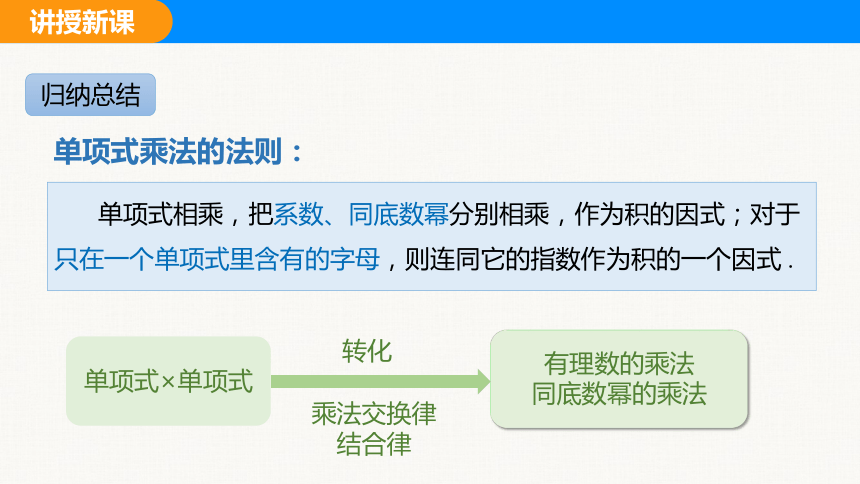
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
单项式×单项式
有理数的乘法
同底数幂的乘法
转化
乘法交换律 结合律
单项式乘法的法则:
归纳总结
例1:计算:
(1) (2)
解:(1)
=
=
单项式的乘法步骤:
①积的系数的确定,包括符号的计算;
②同底数幂相乘;
③单独出现的字母.
例1:计算:
(1) (2)
解:(2)
(1)注意按顺序运算,有乘方,先算乘方,再算单项式相乘;
(2)不要漏掉只在一个单项式里含有的字母因式;
随堂小练习
下列计算正确的有( )
①;②;
③; ④
A.0个 B.1个
C.2个 D.3个
B
例2:已知求的值.
解:因为,
所以,
即.
所以
例3:已知与的积与是同类项,求的值.
解得
解:∵ -2x3m+1y2n与7x5m-3y5n-4的积与x4y是同类项,
∴ 2n+5n-4=1,3m+1+5m-3=4,
∴ m2+n= .
m= , n = ,
例4:2021年5月15日7时18分,天问一号探测器着陆火星,迈出了我国星际探测征程的重要一步,也使我国成为第二个成功登陆火星的国家.天问一号从地球飞行进入环火轨道的里程相当于绕地球圈,它的这一飞行里程约为多少千米?(地球半径约为,取3.14)
解:
=(km)
答:它的这一飞行里程约km.
一个长方体的长为 cm,宽为cm,高为cm,则它的体积是__________________.
cm3
随堂小练习
方法总结:掌握长方形的面积公式和单项式乘单项式法则是解题的关键.
例5:有一块长为xm,宽为ym的长方形空地,现在
要在这块地中规划一块长 xm,宽 ym的长方形
空地用于绿化,求绿化的面积和剩下的面积.
解:长方形的面积是m2,绿化的面积是
× = (m2),
则剩下的面积是 - xy=(m2).
1. 如图,已知四边形和四边形都是长方形,则它们的面积之和为( )
A.
B.
C.
D.
C
习题1
习题2
2.计算:= .
习题3
3.计算
(1); (2); (3);
(3)原式=
=.
解:(1)原式=
=;
(2)原式=
=;
习题4
4.已知与的积与是同类项,求的值.
解:
因为与是同类项,
所以
解得
若求的值.
因为
解:
所以
所以
即
解得
所以
拓展提升
单项式与单项式相乘
单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
(1)不要出现漏乘现象;
(2)有乘方运算,先算乘方,再算单项式相乘.
注意
8.2.1 单项式与单项式相乘
学习目标及重难点
1.掌握单项式与单项式相乘的运算法则.(重点)
2.能够灵活地进行单项式与单项式相乘的运算.(难点)
单项式:
多项式:
下列整式中哪些是单项式,哪些是多项式?
a, ,
2
a,
,
探索1:单项式与单项式相乘
问题1:光的速度大约是 km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要约4年才能到达地球,如果1年以 s计算,地球与这颗恒星的距离约为多少千米?
如何计算?
问题1:光的速度大约是 km/s,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要约4年才能到达地球,如果1年以 s计算,地球与这颗恒星的距离约为多少千米?
因而,地球与这颗恒星的距离约为 km.
交流:1. 下面的运算用了哪些性质?
乘法交换律,乘法结合律以及同底数幂的乘法
因而,地球与这颗恒星的距离约为 km.
乘法交换律、结合律
同底数幂的乘法
( ×)×(××)
交流:2.如果把下面算式中的数字换成字母,该如何计算呢
算式:
(单项式与单项式相乘)
=
(乘法交换律和结合律)
=
(同底数幂相乘)
=
交流:3. 完成下面计算:
;
从以上的计算过程中,你能归纳出单项式乘法法则吗?
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
单项式×单项式
有理数的乘法
同底数幂的乘法
转化
乘法交换律 结合律
单项式乘法的法则:
归纳总结
例1:计算:
(1) (2)
解:(1)
=
=
单项式的乘法步骤:
①积的系数的确定,包括符号的计算;
②同底数幂相乘;
③单独出现的字母.
例1:计算:
(1) (2)
解:(2)
(1)注意按顺序运算,有乘方,先算乘方,再算单项式相乘;
(2)不要漏掉只在一个单项式里含有的字母因式;
随堂小练习
下列计算正确的有( )
①;②;
③; ④
A.0个 B.1个
C.2个 D.3个
B
例2:已知求的值.
解:因为,
所以,
即.
所以
例3:已知与的积与是同类项,求的值.
解得
解:∵ -2x3m+1y2n与7x5m-3y5n-4的积与x4y是同类项,
∴ 2n+5n-4=1,3m+1+5m-3=4,
∴ m2+n= .
m= , n = ,
例4:2021年5月15日7时18分,天问一号探测器着陆火星,迈出了我国星际探测征程的重要一步,也使我国成为第二个成功登陆火星的国家.天问一号从地球飞行进入环火轨道的里程相当于绕地球圈,它的这一飞行里程约为多少千米?(地球半径约为,取3.14)
解:
=(km)
答:它的这一飞行里程约km.
一个长方体的长为 cm,宽为cm,高为cm,则它的体积是__________________.
cm3
随堂小练习
方法总结:掌握长方形的面积公式和单项式乘单项式法则是解题的关键.
例5:有一块长为xm,宽为ym的长方形空地,现在
要在这块地中规划一块长 xm,宽 ym的长方形
空地用于绿化,求绿化的面积和剩下的面积.
解:长方形的面积是m2,绿化的面积是
× = (m2),
则剩下的面积是 - xy=(m2).
1. 如图,已知四边形和四边形都是长方形,则它们的面积之和为( )
A.
B.
C.
D.
C
习题1
习题2
2.计算:= .
习题3
3.计算
(1); (2); (3);
(3)原式=
=.
解:(1)原式=
=;
(2)原式=
=;
习题4
4.已知与的积与是同类项,求的值.
解:
因为与是同类项,
所以
解得
若求的值.
因为
解:
所以
所以
即
解得
所以
拓展提升
单项式与单项式相乘
单项式乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
(1)不要出现漏乘现象;
(2)有乘方运算,先算乘方,再算单项式相乘.
注意
