2025年九年级数学中考三轮冲刺练习圆的综合压轴题训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺练习圆的综合压轴题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 05:14:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺练习圆的综合压轴题训练
1.如图1,CD是⊙O的直径,弦AB与CD交于点E,连接AC、BD.
(1)求证:△ACE∽△DBE;
(2)如图2,已知∠CAB+∠ABD+∠C+∠D=180°,连接BO并延长,交⊙O于点G,交AC于点F,连接AG.
①若AB=2,tan∠CAE=3,求AG的长;
②设tan∠CAE=x,y,求y关于x的函数关系式.
2.如图1,点A,B,C在圆O上运动,满足AB2=BC2+AC2,过点A的切线交BC延长线于点D.
(1)求证:∠DAC=∠CBA;
(2)记△ABC,△ACD,△ABD的面积为S1,S2,S,若,求tanD;
(3)如图2,点Q是线段BC上一动点(Q不与B,C重合),QP⊥AD于P,交AC于点M.若tanD,设x,且y=PD ,试求y关于x的函数解析式,并写出自变量x的取值范围.
3.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M是线段DC延长线上的一点,连结MA交⊙O于点F,连结DF交AB于点G,连结AD,BD,CF.
(1)求证:△MAD∽△DAF.
(2)若AD=2BE,求tan∠AFD的值.
(3)在(2)的条件下,设tan∠M=x,y.
①求y关于x的函数表达式;
②若E为BG的中点,求的值.
4.如图,AB为⊙O的直径,弦CD⊥AB于点E,G为劣弧AD上一动点,AG与CD的延长线交于点F,连接AC、AD、CG、DG.tan∠AGC=x.
(1)求证:∠AGC=∠DGF;
(2)若,求y与x的函数关系式;
(3)设∠GDC﹣∠GCD=α,∠F=β.
①求α与β的数量关系;
②当β=45°,且S△CAG=S△CAD时,求x的值.
5.如图1,BC是⊙O的弦,OD⊥BC于D交圆于点A.E是上任意一点(不与A,B重合),连结BE,CE,在线段BE,CE上各取一点F,G,使得BF=CG,连结AF,AG,FG,并取FG中点M,连结DM.
(1)求证:AF=AG;
(2)求证:.
(3)如图2,当CE是⊙O直径,F是BE中点时,连结OM,设,,用x的代数式表示y.
6.如图1,A,B,C为⊙O上不重合的三点,GC为⊙O的切线,∠G+∠A=90°.
(1)求证:GB为⊙O的切线;
(2)若△ABC为等腰三角形,∠BAC<45°,tan∠BAC,求的值;
(3)如图2,若AB为直径,M为线段AC上一点且GM⊥GB,AM2+OB2﹣3GB2+8GB﹣8=0,0<GB<2,求S四边形MGBA的最大值.
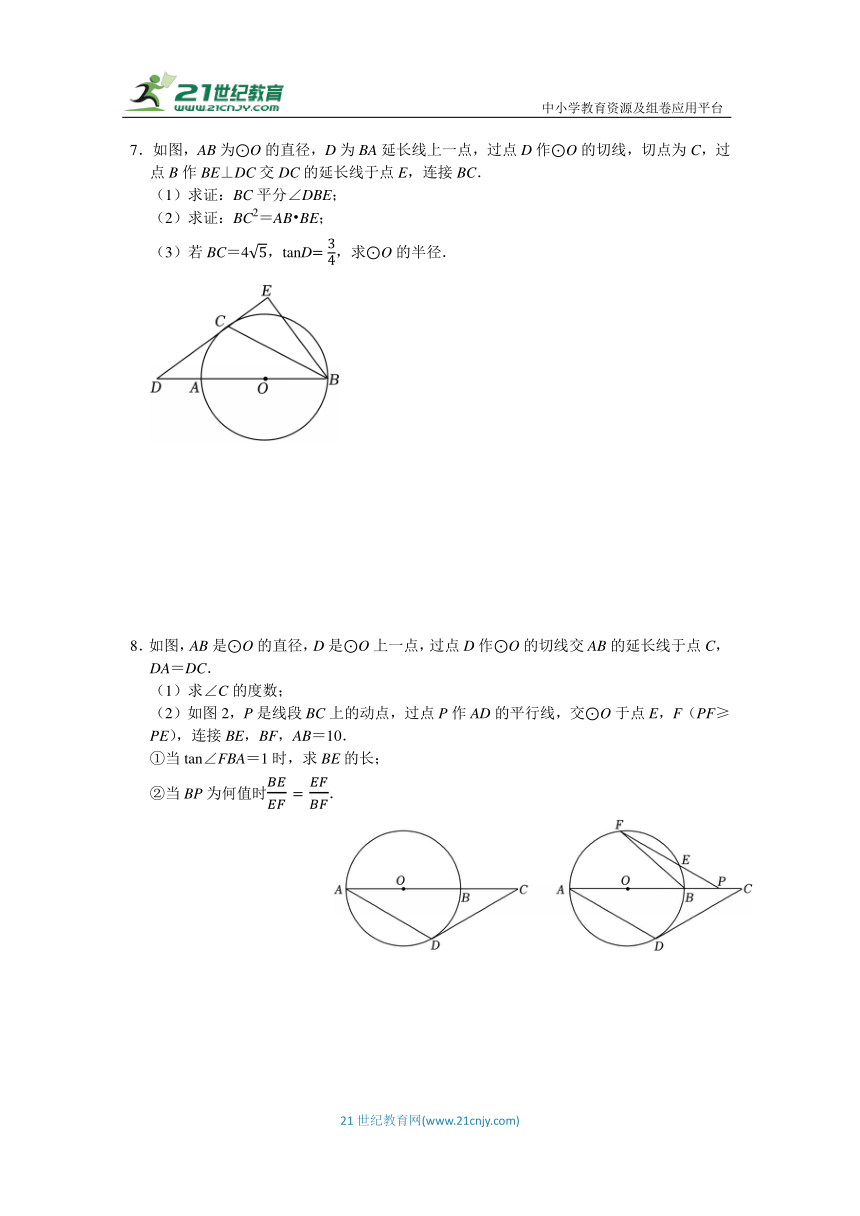
7.如图,AB为⊙O的直径,D为BA延长线上一点,过点D作⊙O的切线,切点为C,过点B作BE⊥DC交DC的延长线于点E,连接BC.
(1)求证:BC平分∠DBE;
(2)求证:BC2=AB BE;
(3)若BC=4,tanD,求⊙O的半径.
8.如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙O的切线交AB的延长线于点C,DA=DC.
(1)求∠C的度数;
(2)如图2,P是线段BC上的动点,过点P作AD的平行线,交⊙O于点E,F(PF≥PE),连接BE,BF,AB=10.
①当tan∠FBA=1时,求BE的长;
②当BP为何值时.
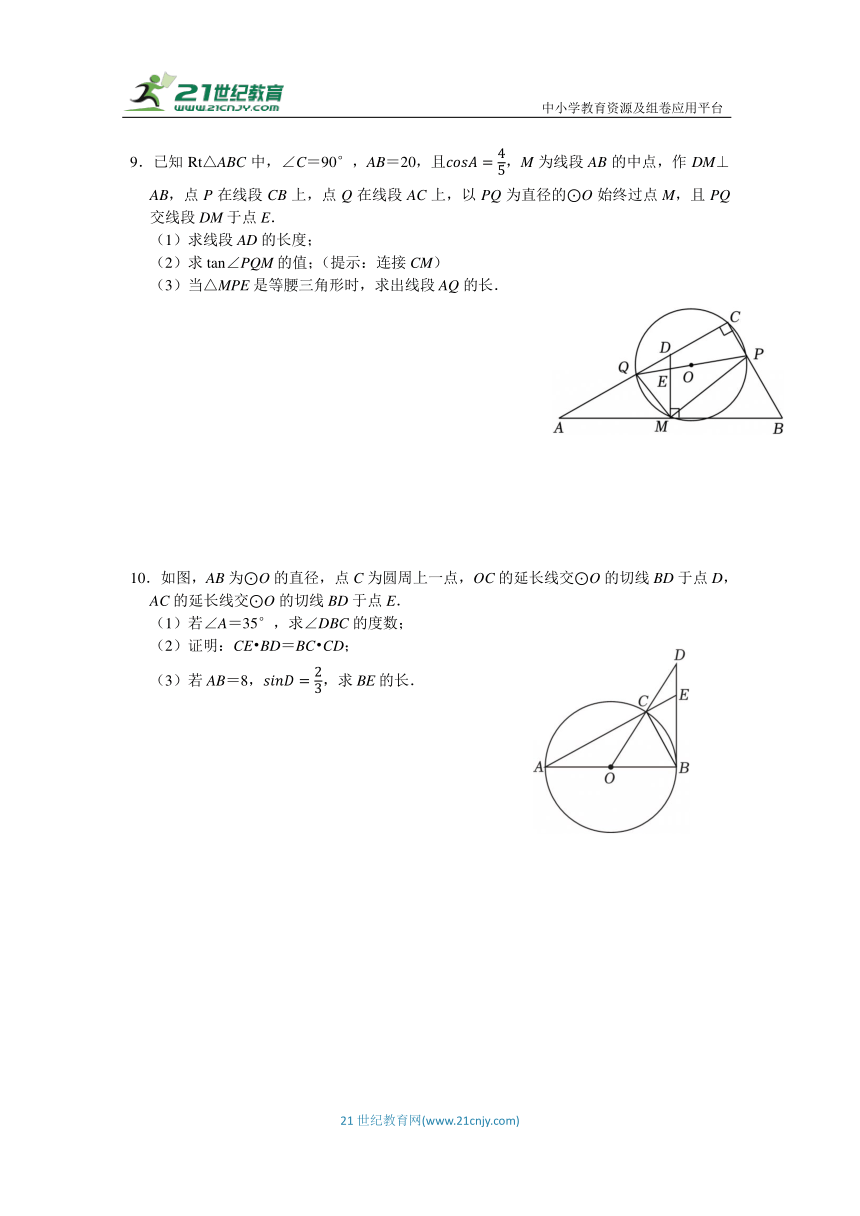
9.已知Rt△ABC中,∠C=90°,AB=20,且,M为线段AB的中点,作DM⊥AB,点P在线段CB上,点Q在线段AC上,以PQ为直径的⊙O始终过点M,且PQ交线段DM于点E.
(1)求线段AD的长度;
(2)求tan∠PQM的值;(提示:连接CM)
(3)当△MPE是等腰三角形时,求出线段AQ的长.
10.如图,AB为⊙O的直径,点C为圆周上一点,OC的延长线交⊙O的切线BD于点D,AC的延长线交⊙O的切线BD于点E.
(1)若∠A=35°,求∠DBC的度数;
(2)证明:CE BD=BC CD;
(3)若AB=8,,求BE的长.
11.如图,⊙O是△ABC的外接圆,AC是⊙O的直径,过圆心O的直线PF⊥AB于D,交⊙O于E,F,PB是⊙O的切线,B为切点,连接AP,AF.
(1)求证:直线PA为⊙O的切线;
(2)求证:AC2=4OD OP;
(3)若BC=6,,求AC的长.
12.如图1,在Rt△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是⊙O的切线.
(1)求∠CDB的度数;
(2)若BP=3,∠P=∠PDB,求图(1)中阴影部分的周长;
(3)如图(2),若AM=BM,连接DM,交AB于点N,若tan∠DMB,求MN:MD的值.
13.如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,过弧BD上一点,过E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE
(1)求证:EG是⊙O的切线;
(2)求证:GF2=GD GC;
(3)延长AB交GE的延长线于点M.若tanG,HC=4,求EM的值.
14.如图,已知⊙O,为△ABC的外接圆,AC为⊙O的直径,BA=BC,过点B作射线BM,使得∠CBM=∠BAC,点P为射线BM上的一个动点,连接PC并延长交⊙O于点D,连接AD,BD.
(1)求证:BM为⊙O的切线;
(2)设BD=x,四边形ABCD的面积为y.
①求y关于x的函数关系式;
②当S△BCD:S△BCP=7:9,AC=6时,求y的值;
(3)已知E为CD的中点,连接AE交BD于点F,连接FC,若,试探究线段FA,FB,FC能否构成一个三角形,若能,请证明你的结论,并判断三角形的形状;若不能,请说明理由.
15.如图1,以AB为直径作⊙O,点C是直径AB上方半圆上的一点,连结AC,BC,过点C作∠ACB的平分线交⊙O于点D,连结AD,过点D作⊙O的切线交CB的延长线于点E.
(1)求证:DE∥AB.
(2)若⊙O的半径为1,求CA CE的最大值.
(3)如图2,连结AE,若,求tan∠AEC的值.
参考答案
1.【解答】(1)证明:∵∠A=∠D,∠B=∠C,
∴△ACE∽△DBE
(2)①∵∠CBA=∠D,∠B=∠C,
∴∠CAB+∠C=90°,
∴CD⊥AB,
又∵CD过圆心,
∴AE=BE=1,
在Rt△AEC中,,
∴CE=3,
设OE=x,则OC=3﹣x=OB,
在Rt△OEB中,由勾股定理得:OB2=OE2+BE2,
即(3﹣x)2=x2+1,
解得:,
∵OG=OB,AE=BE,
∴OE是△AGB的中位线,
∴;
②∵BG是⊙O的直径,
∴∠BAG=90°,
∵∠BAG=∠BEO=90°,
∴OC∥AG,
∴△GAF∽△OCF,
,
设AE=t,在Rt△ACE中,,
∴CE=tx
设OE=d,则OC=tx﹣d=OB,
在Rt△OEB中,由勾股定理得:OB2=OE2+BE2,
即(tx﹣d)2=d2+t2,
解得:,,
,
∴.
2.【解答】(1)证明:在△ABC中,AB2=BC2+AC2,
∴∠ACB=90°,则∠CAB+∠CBA=90°,
∵AD为圆O的切线,
∴∠DAB=90°,即∠DAC+∠CAB=90°,
∴∠DAC=∠CBA;
(2)解:在Rt△ACD中,;在Rt△ACB中,;
由(1)知∠DAC=∠CBA,则∠D=∠CAB,
∴,
设,
由得,则,即,
∴平方并整理得,再平方得到(3k﹣2)2=4(k+1),解得或k=0(舍),
∴,则;
(3)解:∵,
设CD=a,则,
设,则CQ=xBC=2ax,
∵QP⊥AD,
∴∠DPQ=90°,
由(1)知∠ACD=90°,
∴△QDP∽△ADC,则,
∴DQ DC=AD PD;
∵∠APM=∠ACD=90°,∠PAM=∠CAD,
∴△AMP∽△ADC,则,
∴AM AC=AP AD;
∴
,
∵PQ∥AB,
∴,
∴.
3.【解答】(1)证明:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴,
∴∠AFD=∠ADC,
∵∠FAD=∠DAM,
∴△MAD∽△DAF;
(2)解:∵AD=2BE,
∴设BE=a,则AD=2a.
∵AB是⊙O的直径,
∴∠ADB=90°,
∵CD⊥AB,
∴△AED∽△ADB,
∴.
∴,
∴AB=5a.
∴AE=AB﹣BE=4a,
∴DE2a.
∴tan∠ADC2.
由(1)知:∠AFD=∠ADC,
∴tan∠AFD=tan∠ADC=2;
(3)解:①过点G作GH⊥AD于点H,如图,
则tan∠ADF.
由(1)知:△MAD∽△DAF,
∴∠M=∠ADF,
∵tan∠M=x,
∴tan∠ADFx,
∴GH=xHD.
∵tan∠EAD,
∴tan∠GAH.
设GH=m,则AH=2m,
∴AGm.
∴xHD=m,
∴HD.
∵GH⊥AD,AD⊥BD,
∴GH∥BD,
∴,
∴y=2x.
②过点A作AK⊥DF于点K,过点C作CN⊥DF于点N,如图,
∵E为BG的中点,DE⊥BG,
∴DE垂直平分BG,BE=EG=a,
∴AG=AB﹣BE=EG=3a,DGa.
∵AB是⊙O的直径,AB⊥CD,
∴DE=EC=2a,
∴CD=4a.
∵sin∠EDG,
∴,
∴CNa.
∵∠AKG=∠DEG=90°,∠AGK=∠DGE,
∴△AKG∽△DEG,
∴,
∴,
∴AKa.
∴.
4.【解答】(1)证明:如图1,连接BG,
∵直径AB⊥弦CD,
∴,
∴∠CGB=∠BGD,
∵AB是⊙O的直径,
∴∠AGB=90°,
∴∠FGB=180°﹣∠AGB=90°,
∴∠AGB﹣∠CGB=∠FGB﹣∠BGD,即∠AGC=∠DGF;
(2)解:∵直径AB⊥弦CD,
∴AC=AD,CECD,
∴∠ACD=∠ADC,
∵∠ADC=∠AGC,
∴∠AGC=∠ACD,
又∵∠CAG=∠FAC,
∴△ACG∽△AFC,
∴,
∴AC2=AG AF;
在Rt△ACE中,∠ACE=∠AGC=∠DGF,则AE=CE tan∠ACE=xCE,
∴AC2=CE2+AE2=(1+x2)CE2,
∴1+x2,
∴y=x2+1;
(3)解:①如图2,设AB,CG交于点M,连接MD,OC,OG,过点G作GP⊥AC于点P,过点D作DQ⊥AC于点Q,则GP∥DQ,
∵直径AB⊥弦CD,
∴AC=AD,MC=MD,
又∵AM=AM,
∴△AMC≌△AMD(SSS),
∴∠ACM=∠ADM,
∵∠ACG=∠ADG,
∴∠ADM=∠ADG=∠ACG,
由(2)知△ACG∽△AFC,
∴∠ACG=∠AFC=β,
∵MC=MD,
∴∠MCD=∠MDC=∠GCD,
∴∠GDC﹣∠GCD=∠MDG=α,
∵∠MDG=∠ADM+∠ADG=2β,
∴a=2β;
②∵S△CAG=S△CAD,S△CAGAC GP,S△CADAC DQ,
∴GP=DQ,
∵GP∥DQ,
∴四边形GPQD是矩形,
∴GD∥AC,
∴∠FDG=∠ACF=∠ADC=∠AGC=∠FGD,
∵∠F=45°,
∴∠FGD=∠AGC(180°﹣45°)=67.5°,
∴∠DGC=180°﹣∠FGD﹣∠AGC=45°,
∵∠MDG=90°,
∴△MDG是等腰直角三角形,
∴MGMDMC,
∵∠ACG=∠AFC=45°,
∴∠AOG=90° 即OG⊥AB,
∵AB⊥CF,
∴OG∥CF,
∴△GMO∽△CME,
∴,
∴OG=OA=OCCE,
在Rt△OEC 中,OECE,
在Rt△AEC中,tan∠ACE1,
∵∠ACE=∠DGF,
∴x=1.
5.【解答】(1)证明:连接AB,AC,如图,
∵BC是⊙O的弦,OD⊥BC,
∴BD=DC,
∴AD为BC的垂直平分线,
∴AB=AC,
∵,
∴∠EBA=∠ECA.
在△AFB和△AGC中,
,
∴△AFB≌△AGC(SAS),
∴AF=AG;
(2)证明:连接AM,如图,
由(1)知:△AFB≌△AGC,
∴∠FAB=∠GAC,AF=AG,
∴∠FAB+∠BAG=∠BAG+∠GAC.
即∠FAG=∠BAC.
∵AB=AC,
∴△AFG和△ABC为顶角相等的等腰三角形,
∴∠AGF=∠AFG=∠ABC=∠ACB,
∵AD⊥BC,
∴sin∠AGF=sin∠ACB.
∵AF=AG,FM=MG,
∴AM⊥FG,
∴∠AMG=∠ADC=90°.
∵∠AGF=∠ACB,
∴△AMG∽△ADC,
∴,∠MAG=∠DAC,
∴∠MAG﹣∠DAG=∠DAC﹣∠DAG,
∴∠MAD=∠GAC,
∴△MAD∽△GAC,
∴,
∴sin∠AGF;
(3)解:连接AE,AC,FC,FC与AD交于点H,连接MH,如图,
∵CE是⊙O直径,
∴OE=OC,∠EAC=∠EBC=90°,
∵AD⊥BC,
∴AD∥BE,
∵BD=DC,
∴DH,OH分别为△CFB和△CEF的中位线,
∴DHBF,OHEF,FH=HC,
∵EF=BF,
∴DH=OH.
∵FM=MG,FH=HC,
∴MH∥CG,MHCG.
由(1)知:BF=CG,
∴MH=DH=OH.
∴∠HMO=∠HOM,∠HMD=∠HDM,
∵∠HMO+∠HOM+∠HMD+∠HDM=180°,
∴∠HMO+∠HMD=90°,
∴∠DMO=90°,
∴∠DMO=∠EAC=90°.
由(2)知:△MAD∽△GAC,
∴∠MDA=∠GAC,
∴△DMO∽△CAE,
∴.
∵,
∴设CG=a,则OG=ax,
∴OC=a+ax,
∴CE=2OC=2a+2ax.
∵BF=CG,
∴BF=a,EB=2BF=2a,ODEB=a,
∴BC2a,
∴CDBC=a,
∵AD=OA+OD=a+ax+a=2a+ax,
∴AC2=AD2+CD22a2x2+6a2x+4a2,
∴AEa,
∴,
∴y.
6.【解答】(1)证明:连接OB,OC,
∵GC 为⊙O 的切线,
∴∠GCO=90°,
∵,
∴∠G+2∠A=∠G+∠COB=180°,
∴∠GBO=180°﹣90°=90°,
∵点B在⊙O上,
∴GB为⊙O的切线;
(2)解:设⊙O的半径为r,连接OG交BC于点D,连接OC,OB,
∵OC=OB,GC=GB,
∴BC⊥OD,且D为BC的中点,
∴∠BAC,
∵,
∴,,
①当BC为底边,点A在弦BC所对的优弧上时,AC=AB,
∴BC=2CD,AD⊥BC,
∵OC=OB,
∴∠COGCOB,
∵∠CABCOB,
∴∠COG=∠CAB,
∴BC=2CD=2 r sin∠COG=2 r sin∠BAC=6,
连接OA,∵AC=AB,
∴A,O,D,G四点共线,
∴,
∴;
②当AB为底边时,AC=BC,
∴AB⊥OC于点F,
令CF=3t,则,
∵OF2+BF2=OB2,
即(r﹣3t)2+(4t)2=r2
解得,
∴,,
过点G作AB的垂线,垂足为点H,
∵AB⊥OC,CG⊥OC,
∴四边形CFHG为矩形,
∴AH=HF+FA=CG+BF=rtan∠COG+BF=rtan∠BAC+BFrr,,
∴,
由①知BC=2CD=2 r sin∠BACr,
∴;
③当AC为底边时,由对称性,与AB为底边时的情况相同.
综上所述,或;
(3)解:延长AC,BG交于点D,
∵∠CGD=180°﹣∠BGC=2∠A,∠D=90°﹣∠A,
∴∠D=∠DCG,
∴CG=DG,
由(1)得CG=GB,
∴GB=DG,G是BD的中点,
∵GM⊥GB,AB⊥GB,
∴GM∥AB,M是AD的中点.
连接OM,则四边形OMGB为矩形,
∴OM=GB,
∴OB2=OA2=AM2﹣OM2=AM2﹣GB2,
设GB=x,AM=y,则0<x<2,
∵AM2+OB2﹣3GB2+8GB﹣8=0,
∴OB2=y2﹣x2=x2﹣4x+4=(x﹣2)2,
∴S四边形MGBA=3S△AOM=3xx2+3x(x﹣1)2,
∴当x=1时,四边形MGBA的面积最大为.
7.【解答】(1)证明:连接OC,
∵CD是⊙O的切线,
∴OC⊥DE,
∵DE⊥BE,
∴OC∥BE,
∴∠EBC=∠OCB,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC=∠EBC,
∴BC平分∠DBE.
(2)证明:连接AC,
∵AB是直径,
∴∠ACB=90°,
∵BE⊥CD,
∴∠BED=90°,
∴△ABC∽△CBE,
∴,
∴BC2=AB BE.
(3)解:设⊙O的半径为r,
∵,
∴,
∴,
∴,
∵∠DCO=90°,∠BED=90°,
∴△DCO∽△DEB,
∴,即,
∴,
∵AB BE=80,
∴,
∴r1=5,r2=﹣5(舍去),
∴⊙O的半径为5.
8.【解答】解:(1)连接OD,如图:
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COD=2∠A,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠C+∠COD=90°,即∠C+2∠A=90°,
又∵DA=DC,
∴∠A=∠C,
∴∠C=30°;
(2)①连接AF,OF,如图:
∵AB是直径,
∴∠AFB=90°,
∵tan∠FBA=1,
∴∠FBA=45°,
∴△ABF为等腰直角三角形,
∴AF=BF=5,OF⊥AB,
∵PF∥AD,
∴∠FPO=∠DAC=∠C=30°,
∴PF=2OF=10,OPOF=5,
∴BP=OP﹣OB=55,
∵∠FAB+∠FEB=180°,∠PEB+∠FEB=180°,
∴∠FAB=∠PEB,
又∵∠EPB=∠APF,
∴△AFP∽△EBP,
∴,
∴BE();
②过点B作BG⊥FP于G,连接OE,过O作ON⊥EF于N,如图:
∴∠BGE=∠BGP=90°,
∴∠BGE=∠AFB,
∵∠BEP=∠FAP,
∴△PEB∽△PAF,
∴,
∴BP AP=PE PF,
设BG=x,
∵∠FPA=∠DAC=30°,
∴BP=2x,PGx,
∴AP=10+2x,OP=5+2x,
∴ONOPx,PN(5+2x),
在Rt△NOE中,EN2=OE2﹣ON2=25﹣(x)2,
∵ON⊥EF,
∴FN=EN,EF=2EN,
在Rt△EBG中,BE2=BG2+EG2,
在Rt△BFG中,BF2=BG2+FG2,
∵FG=PN+FN﹣PG,EG=PN﹣PG﹣FN,
∴FG EG=(PN﹣PG)2﹣FN2[25﹣(x)2]=x2+5x,FG+EG=2(PN﹣PG)=5,
∴BE2 BF2=(BG2+EG2)(BG2+FG2)
=BG4+(EG2+FG2)BG2+(EG FG)2
=BG4+[(EG+FG)2﹣2EG FG]BG2+(EG FG)2
=x4+[75﹣2x2﹣10x]x2+(x2+5x)2
=100x2,
∴BE BF=10x,
∵,
∴BE BF=EF2=4EN2,
即10x=4[25﹣(x)2],
解得:x(舍去)或,
∴BP=2x.
9.【解答】解:(1)∵M为AB中点,AB=20,
∴,
∵DM⊥AB,
在Rt△ADM中,即:,
∴;
(2)连接CM,
∵M是Rt△ABC斜边上的中点,
∴,
∴∠A=∠ACM,∠B=∠BCM,
∵∠MPQ=∠ACM,
∴∠A=∠MPQ,
∵QP是⊙O的直径,
∴∠ACB=∠PMQ=90°,
∴∠PQM=∠ABC=∠BCM,
∵,
∴,
∵;
∴;
(3)∵∠QMA+∠QMD=90°,∠DMP+∠QMD=90°,
∴∠QMA=∠DMP,
由(1)知∠A=∠MPQ.
∴△AMO∽△PME,
当△PME是等腰三角形时,有△AMQ为等腰三角形,
当AM=AQ时,AQ=10,
当AM=MQ时,∠A=∠AQM=∠ACM,而∠AQM>∠ACM,所以这种情况不存在;
当AQ=MQ时,∠A=∠QMA,
而∠A+∠ADM=90°,∠QMA+∠DMQ=90°,
∴∠ADM=∠DMQ,
∴,
由(1)知,可得;
∴AQ=10或.
10.【解答】(1)解:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC=90°﹣∠A=55°,
∵BD与⊙O相切于点B,
∴BD⊥AB,
∴∠DBC=90°﹣∠ABC=35°,
(2)证明:∵OA=OC,
∴∠A=∠ACO,又∠ACO=∠DCE,
∴∠DCE=∠A=∠DBC,
又∵∠D=∠D,
∴△DCE∽△DBC,
∴,
∴CE BD=BC CD;
(3)解:∵AB=8,
∴,
,
,
∴DC=OD﹣OC=6﹣4=2,,
∵∠DBC=∠DCE,∠D=∠D,
∴△DBC∽△DCE,
,
,
,
∴BE的长是.
11.【解答】(1)证明:连接OB,
∵PB是⊙O的切线,
∴∠PBO=90°,
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB,
又∵PO=PO,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO=90°,
∵OA为圆的半径,
∴直线PA为⊙O的切线;
(2)证明:∵∠PAO=∠PDA=90°,
∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°,
∴∠OAD=∠OPA,
∴△OAD∽△OPA,
∴,
∴OA2=OD OP,
又∵AC=2OA,
∴AC2=4OD OP;
(3)解:∵OA=OC,AD=BD,BC=6,
∴ODBC=3,
设AD=x,
∵tan∠F,
∴FD=2x,OA=OF=2x﹣3,
在Rt△AOD中,由勾股定理,得,
(2x﹣3)2=x2+32,
解之得,x1=4,x2=0(不合题意,舍去),
∴AD=4,OA=2x﹣3=5,
∵AC是⊙O的直径,
∴AC=2OA=10.
∴AC的长为10.
12.【解答】解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=∠ADB=90°;
(2)连接OD,
∵∠P=∠PDB,
∴BD=BP=3,
∵PD是⊙O的切线,
∴OD⊥PD,
∴∠ODB+∠PDB=90°,∠P+∠POD=90°,
∵∠P=∠PDB,
∴BO=BD=3,
∴OB=BD=OD,
∴△OBD是等边三角形,
∴∠DOB=60°,
∴弧BD的长度π,
在Rt△CDB中,BD=3,∠CBD=30°,
∴CD,BC=2,
∴阴影部分的周长为π+3;
(3)连接OM,过点D作DF⊥AB交于点F,
∵AM=BM,
∴OM⊥AB,
∵,
∴∠DMB=∠DAB,
∴tan∠DMB=tan∠DAB,
∵tan∠DMB,
∴tan∠DAB
设BD=a,则AD=2a,
∴ABa,
∴OMa,
∵AD BD=AB DF,
∴DFa,
∵DF⊥AB,OM⊥AB,
∴OM∥DF,
∴△OMN∽△FDN,
∴,
∴,
∴MN:MD.
13.【解答】解:(1)证明:如图,连接OE,
∵GF=GE,∴∠GFE=∠GEF=∠AFH,
∵OA=OE,∴∠OAE=∠OEA,
∵∠AFH+∠FAH=90°,
∴∠GEF+∠AEO=90°,
∴∠GEO=90°,∴GE⊥OE,
∴EG是⊙O的切线;
(2)连接DE,易得△GDE∽△GEC,
∴,
∴GE2=GC GD,
又∵GF=GE,
∴GF2=GC GD;
(3)如图,连接OC.
设⊙O的半径为r.
在Rt△AHC中,
,
∵,
∴,
在Rt△HOC中,
∵OC=r,,,
∴,
∴,
∵GM∥AC,
∴∠CAH=∠M,
∵∠OEM=∠AHC,
∴△AHC∽△MEO,
∴,
∴,
∴.
14.【解答】(1)证明:连接OB,如图,
∵AC为⊙O的直径,
∴∠ABC=90°.
∵,
∴BA=BC,
∴△ABC是等腰直角三角形,
∴∠BAC=∠BCA=45°.
∵OB=OC,
∠OBC=∠OCB=45°.
∵∠CBM=∠BAC,
∴∠CBM=45°,
∴∠OBM=∠CBM+∠CBO=90°,
∴BM⊥OB.
∵OB为⊙O的半径,
∴BM为⊙O的切线;
(2)解:①如解图②,作BG⊥CD于点G,BH⊥DA交DA的延长线于点H,如图,
∵BG⊥CD,BH⊥DH,
∴∠BHD=∠BGD=90°.
∵AC 为⊙O的直径,
∴∠ADC=90°,
∴四边形BGDH为矩形,
∵
∴BA=BC,∠ADB=∠BDC.
∵BG⊥CD,BH⊥DH,
∴BH=BG,
∴矩形BGDH为正方形,
在Rt△ABH和Rt△CBG中,
,
∴Rt△ABH≌Rt△CBG(HL),
∴S△ABH=S△CBC,
∴S四边形ABCD=S正方形BGDH,
∵BD2,
∴;
②由(1)知:∠PBC=∠BAC=45°.
∴∠PDB=∠BAC=∠PBC=45°,
∵∠BPC=∠DPB,
∴△BCP∽△DBP,
∴.
∵S△BCD:S△BCP=7:9,
∴,
∴,
∴.
在Rt△ABC中,
∵,
∴BD=3,
∴BD=4,
即 .
∴;
(3)线段FA,FB,FC能构成一个三角形,三角形的形状为直角三角形,证明如下:
如图,
∵,∠ABD=∠ACD,
∴.
由(2)①知:∠ADC=90°,
∴tan∠ACD,
∴.
∵E为CD的中点,
∴,
∴AD=ED,
∴△ADE是等腰直角三角形.
由(2)①知,∠ADB=∠BDC,
∴DB垂直平分AE,
∴,
∴,
∴,
∵∠CEF=∠AEC,
∴△CEF∽△AEC,
∴,
∴.
由(1)知:△ABC是等腰直角三角形,
∴,
∴FC=AB,
在Rt△ABF中,FA2+FB2=AB2,
∴FA2+FB2=FC2,
∴线段FA,FB,FC能构成一个直角三角形.
15.【解答】(1)证明:连接OD,如图,
∵DE为⊙O的切线,
∴OD⊥DE.
∵AB为直径,
∴∠ACB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠AOD=2∠ACD=90°,
∴OD⊥AB,
∴DE∥AB;
(2)解:∵DE∥AB,
∴∠E=∠ABC,
∵∠ABC=∠ADC,
∴∠E=∠ADC,
∵∠ECD=∠ACD,
∴△DCE∽△ACD,
∴,
∴CD2=CA CE.
∴当CD取得最大值时,CA CE的值最大,
∵CD是圆O的弦,
∴CD为直径时取得最大值,
∵⊙O的半径为1,
∴CD的最大值为2,
∴CA CE的最大值为4.
(3)解:设tan∠ABC=x,tan∠AEC=y,
∵AB为直径,
∴∠ACB=90°,
∴y=tan∠AEC.
由(2)知:,
∴y=tan∠AEC,
过点D作DF⊥CE于点F,如图,
设EF=a,
∵DE∥AB,
∴∠ABC=∠DEC,
∴tan∠DEC=tan∠ABC=x,
∴DF=EF tan∠DEC=ax,
∵∠DCE=45°,
∴CF=DF=ax,
∴CDDFax,CE=ax+a,
∴y,
∵,
∴,
∴:7:3,
∴x:y=7:3,
∴yx.
把yx代入y中,
∴,
解得:x1,x2,
当x时,y,
当x时,y.
∴tan∠AEC的值为或.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺练习圆的综合压轴题训练
1.如图1,CD是⊙O的直径,弦AB与CD交于点E,连接AC、BD.
(1)求证:△ACE∽△DBE;
(2)如图2,已知∠CAB+∠ABD+∠C+∠D=180°,连接BO并延长,交⊙O于点G,交AC于点F,连接AG.
①若AB=2,tan∠CAE=3,求AG的长;
②设tan∠CAE=x,y,求y关于x的函数关系式.
2.如图1,点A,B,C在圆O上运动,满足AB2=BC2+AC2,过点A的切线交BC延长线于点D.
(1)求证:∠DAC=∠CBA;
(2)记△ABC,△ACD,△ABD的面积为S1,S2,S,若,求tanD;
(3)如图2,点Q是线段BC上一动点(Q不与B,C重合),QP⊥AD于P,交AC于点M.若tanD,设x,且y=PD ,试求y关于x的函数解析式,并写出自变量x的取值范围.
3.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M是线段DC延长线上的一点,连结MA交⊙O于点F,连结DF交AB于点G,连结AD,BD,CF.
(1)求证:△MAD∽△DAF.
(2)若AD=2BE,求tan∠AFD的值.
(3)在(2)的条件下,设tan∠M=x,y.
①求y关于x的函数表达式;
②若E为BG的中点,求的值.
4.如图,AB为⊙O的直径,弦CD⊥AB于点E,G为劣弧AD上一动点,AG与CD的延长线交于点F,连接AC、AD、CG、DG.tan∠AGC=x.
(1)求证:∠AGC=∠DGF;
(2)若,求y与x的函数关系式;
(3)设∠GDC﹣∠GCD=α,∠F=β.
①求α与β的数量关系;
②当β=45°,且S△CAG=S△CAD时,求x的值.
5.如图1,BC是⊙O的弦,OD⊥BC于D交圆于点A.E是上任意一点(不与A,B重合),连结BE,CE,在线段BE,CE上各取一点F,G,使得BF=CG,连结AF,AG,FG,并取FG中点M,连结DM.
(1)求证:AF=AG;
(2)求证:.
(3)如图2,当CE是⊙O直径,F是BE中点时,连结OM,设,,用x的代数式表示y.
6.如图1,A,B,C为⊙O上不重合的三点,GC为⊙O的切线,∠G+∠A=90°.
(1)求证:GB为⊙O的切线;
(2)若△ABC为等腰三角形,∠BAC<45°,tan∠BAC,求的值;
(3)如图2,若AB为直径,M为线段AC上一点且GM⊥GB,AM2+OB2﹣3GB2+8GB﹣8=0,0<GB<2,求S四边形MGBA的最大值.
7.如图,AB为⊙O的直径,D为BA延长线上一点,过点D作⊙O的切线,切点为C,过点B作BE⊥DC交DC的延长线于点E,连接BC.
(1)求证:BC平分∠DBE;
(2)求证:BC2=AB BE;
(3)若BC=4,tanD,求⊙O的半径.
8.如图,AB是⊙O的直径,D是⊙O上一点,过点D作⊙O的切线交AB的延长线于点C,DA=DC.
(1)求∠C的度数;
(2)如图2,P是线段BC上的动点,过点P作AD的平行线,交⊙O于点E,F(PF≥PE),连接BE,BF,AB=10.
①当tan∠FBA=1时,求BE的长;
②当BP为何值时.
9.已知Rt△ABC中,∠C=90°,AB=20,且,M为线段AB的中点,作DM⊥AB,点P在线段CB上,点Q在线段AC上,以PQ为直径的⊙O始终过点M,且PQ交线段DM于点E.
(1)求线段AD的长度;
(2)求tan∠PQM的值;(提示:连接CM)
(3)当△MPE是等腰三角形时,求出线段AQ的长.
10.如图,AB为⊙O的直径,点C为圆周上一点,OC的延长线交⊙O的切线BD于点D,AC的延长线交⊙O的切线BD于点E.
(1)若∠A=35°,求∠DBC的度数;
(2)证明:CE BD=BC CD;
(3)若AB=8,,求BE的长.
11.如图,⊙O是△ABC的外接圆,AC是⊙O的直径,过圆心O的直线PF⊥AB于D,交⊙O于E,F,PB是⊙O的切线,B为切点,连接AP,AF.
(1)求证:直线PA为⊙O的切线;
(2)求证:AC2=4OD OP;
(3)若BC=6,,求AC的长.
12.如图1,在Rt△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是⊙O的切线.
(1)求∠CDB的度数;
(2)若BP=3,∠P=∠PDB,求图(1)中阴影部分的周长;
(3)如图(2),若AM=BM,连接DM,交AB于点N,若tan∠DMB,求MN:MD的值.
13.如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,过弧BD上一点,过E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE
(1)求证:EG是⊙O的切线;
(2)求证:GF2=GD GC;
(3)延长AB交GE的延长线于点M.若tanG,HC=4,求EM的值.
14.如图,已知⊙O,为△ABC的外接圆,AC为⊙O的直径,BA=BC,过点B作射线BM,使得∠CBM=∠BAC,点P为射线BM上的一个动点,连接PC并延长交⊙O于点D,连接AD,BD.
(1)求证:BM为⊙O的切线;
(2)设BD=x,四边形ABCD的面积为y.
①求y关于x的函数关系式;
②当S△BCD:S△BCP=7:9,AC=6时,求y的值;
(3)已知E为CD的中点,连接AE交BD于点F,连接FC,若,试探究线段FA,FB,FC能否构成一个三角形,若能,请证明你的结论,并判断三角形的形状;若不能,请说明理由.
15.如图1,以AB为直径作⊙O,点C是直径AB上方半圆上的一点,连结AC,BC,过点C作∠ACB的平分线交⊙O于点D,连结AD,过点D作⊙O的切线交CB的延长线于点E.
(1)求证:DE∥AB.
(2)若⊙O的半径为1,求CA CE的最大值.
(3)如图2,连结AE,若,求tan∠AEC的值.
参考答案
1.【解答】(1)证明:∵∠A=∠D,∠B=∠C,
∴△ACE∽△DBE
(2)①∵∠CBA=∠D,∠B=∠C,
∴∠CAB+∠C=90°,
∴CD⊥AB,
又∵CD过圆心,
∴AE=BE=1,
在Rt△AEC中,,
∴CE=3,
设OE=x,则OC=3﹣x=OB,
在Rt△OEB中,由勾股定理得:OB2=OE2+BE2,
即(3﹣x)2=x2+1,
解得:,
∵OG=OB,AE=BE,
∴OE是△AGB的中位线,
∴;
②∵BG是⊙O的直径,
∴∠BAG=90°,
∵∠BAG=∠BEO=90°,
∴OC∥AG,
∴△GAF∽△OCF,
,
设AE=t,在Rt△ACE中,,
∴CE=tx
设OE=d,则OC=tx﹣d=OB,
在Rt△OEB中,由勾股定理得:OB2=OE2+BE2,
即(tx﹣d)2=d2+t2,
解得:,,
,
∴.
2.【解答】(1)证明:在△ABC中,AB2=BC2+AC2,
∴∠ACB=90°,则∠CAB+∠CBA=90°,
∵AD为圆O的切线,
∴∠DAB=90°,即∠DAC+∠CAB=90°,
∴∠DAC=∠CBA;
(2)解:在Rt△ACD中,;在Rt△ACB中,;
由(1)知∠DAC=∠CBA,则∠D=∠CAB,
∴,
设,
由得,则,即,
∴平方并整理得,再平方得到(3k﹣2)2=4(k+1),解得或k=0(舍),
∴,则;
(3)解:∵,
设CD=a,则,
设,则CQ=xBC=2ax,
∵QP⊥AD,
∴∠DPQ=90°,
由(1)知∠ACD=90°,
∴△QDP∽△ADC,则,
∴DQ DC=AD PD;
∵∠APM=∠ACD=90°,∠PAM=∠CAD,
∴△AMP∽△ADC,则,
∴AM AC=AP AD;
∴
,
∵PQ∥AB,
∴,
∴.
3.【解答】(1)证明:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴,
∴∠AFD=∠ADC,
∵∠FAD=∠DAM,
∴△MAD∽△DAF;
(2)解:∵AD=2BE,
∴设BE=a,则AD=2a.
∵AB是⊙O的直径,
∴∠ADB=90°,
∵CD⊥AB,
∴△AED∽△ADB,
∴.
∴,
∴AB=5a.
∴AE=AB﹣BE=4a,
∴DE2a.
∴tan∠ADC2.
由(1)知:∠AFD=∠ADC,
∴tan∠AFD=tan∠ADC=2;
(3)解:①过点G作GH⊥AD于点H,如图,
则tan∠ADF.
由(1)知:△MAD∽△DAF,
∴∠M=∠ADF,
∵tan∠M=x,
∴tan∠ADFx,
∴GH=xHD.
∵tan∠EAD,
∴tan∠GAH.
设GH=m,则AH=2m,
∴AGm.
∴xHD=m,
∴HD.
∵GH⊥AD,AD⊥BD,
∴GH∥BD,
∴,
∴y=2x.
②过点A作AK⊥DF于点K,过点C作CN⊥DF于点N,如图,
∵E为BG的中点,DE⊥BG,
∴DE垂直平分BG,BE=EG=a,
∴AG=AB﹣BE=EG=3a,DGa.
∵AB是⊙O的直径,AB⊥CD,
∴DE=EC=2a,
∴CD=4a.
∵sin∠EDG,
∴,
∴CNa.
∵∠AKG=∠DEG=90°,∠AGK=∠DGE,
∴△AKG∽△DEG,
∴,
∴,
∴AKa.
∴.
4.【解答】(1)证明:如图1,连接BG,
∵直径AB⊥弦CD,
∴,
∴∠CGB=∠BGD,
∵AB是⊙O的直径,
∴∠AGB=90°,
∴∠FGB=180°﹣∠AGB=90°,
∴∠AGB﹣∠CGB=∠FGB﹣∠BGD,即∠AGC=∠DGF;
(2)解:∵直径AB⊥弦CD,
∴AC=AD,CECD,
∴∠ACD=∠ADC,
∵∠ADC=∠AGC,
∴∠AGC=∠ACD,
又∵∠CAG=∠FAC,
∴△ACG∽△AFC,
∴,
∴AC2=AG AF;
在Rt△ACE中,∠ACE=∠AGC=∠DGF,则AE=CE tan∠ACE=xCE,
∴AC2=CE2+AE2=(1+x2)CE2,
∴1+x2,
∴y=x2+1;
(3)解:①如图2,设AB,CG交于点M,连接MD,OC,OG,过点G作GP⊥AC于点P,过点D作DQ⊥AC于点Q,则GP∥DQ,
∵直径AB⊥弦CD,
∴AC=AD,MC=MD,
又∵AM=AM,
∴△AMC≌△AMD(SSS),
∴∠ACM=∠ADM,
∵∠ACG=∠ADG,
∴∠ADM=∠ADG=∠ACG,
由(2)知△ACG∽△AFC,
∴∠ACG=∠AFC=β,
∵MC=MD,
∴∠MCD=∠MDC=∠GCD,
∴∠GDC﹣∠GCD=∠MDG=α,
∵∠MDG=∠ADM+∠ADG=2β,
∴a=2β;
②∵S△CAG=S△CAD,S△CAGAC GP,S△CADAC DQ,
∴GP=DQ,
∵GP∥DQ,
∴四边形GPQD是矩形,
∴GD∥AC,
∴∠FDG=∠ACF=∠ADC=∠AGC=∠FGD,
∵∠F=45°,
∴∠FGD=∠AGC(180°﹣45°)=67.5°,
∴∠DGC=180°﹣∠FGD﹣∠AGC=45°,
∵∠MDG=90°,
∴△MDG是等腰直角三角形,
∴MGMDMC,
∵∠ACG=∠AFC=45°,
∴∠AOG=90° 即OG⊥AB,
∵AB⊥CF,
∴OG∥CF,
∴△GMO∽△CME,
∴,
∴OG=OA=OCCE,
在Rt△OEC 中,OECE,
在Rt△AEC中,tan∠ACE1,
∵∠ACE=∠DGF,
∴x=1.
5.【解答】(1)证明:连接AB,AC,如图,
∵BC是⊙O的弦,OD⊥BC,
∴BD=DC,
∴AD为BC的垂直平分线,
∴AB=AC,
∵,
∴∠EBA=∠ECA.
在△AFB和△AGC中,
,
∴△AFB≌△AGC(SAS),
∴AF=AG;
(2)证明:连接AM,如图,
由(1)知:△AFB≌△AGC,
∴∠FAB=∠GAC,AF=AG,
∴∠FAB+∠BAG=∠BAG+∠GAC.
即∠FAG=∠BAC.
∵AB=AC,
∴△AFG和△ABC为顶角相等的等腰三角形,
∴∠AGF=∠AFG=∠ABC=∠ACB,
∵AD⊥BC,
∴sin∠AGF=sin∠ACB.
∵AF=AG,FM=MG,
∴AM⊥FG,
∴∠AMG=∠ADC=90°.
∵∠AGF=∠ACB,
∴△AMG∽△ADC,
∴,∠MAG=∠DAC,
∴∠MAG﹣∠DAG=∠DAC﹣∠DAG,
∴∠MAD=∠GAC,
∴△MAD∽△GAC,
∴,
∴sin∠AGF;
(3)解:连接AE,AC,FC,FC与AD交于点H,连接MH,如图,
∵CE是⊙O直径,
∴OE=OC,∠EAC=∠EBC=90°,
∵AD⊥BC,
∴AD∥BE,
∵BD=DC,
∴DH,OH分别为△CFB和△CEF的中位线,
∴DHBF,OHEF,FH=HC,
∵EF=BF,
∴DH=OH.
∵FM=MG,FH=HC,
∴MH∥CG,MHCG.
由(1)知:BF=CG,
∴MH=DH=OH.
∴∠HMO=∠HOM,∠HMD=∠HDM,
∵∠HMO+∠HOM+∠HMD+∠HDM=180°,
∴∠HMO+∠HMD=90°,
∴∠DMO=90°,
∴∠DMO=∠EAC=90°.
由(2)知:△MAD∽△GAC,
∴∠MDA=∠GAC,
∴△DMO∽△CAE,
∴.
∵,
∴设CG=a,则OG=ax,
∴OC=a+ax,
∴CE=2OC=2a+2ax.
∵BF=CG,
∴BF=a,EB=2BF=2a,ODEB=a,
∴BC2a,
∴CDBC=a,
∵AD=OA+OD=a+ax+a=2a+ax,
∴AC2=AD2+CD22a2x2+6a2x+4a2,
∴AEa,
∴,
∴y.
6.【解答】(1)证明:连接OB,OC,
∵GC 为⊙O 的切线,
∴∠GCO=90°,
∵,
∴∠G+2∠A=∠G+∠COB=180°,
∴∠GBO=180°﹣90°=90°,
∵点B在⊙O上,
∴GB为⊙O的切线;
(2)解:设⊙O的半径为r,连接OG交BC于点D,连接OC,OB,
∵OC=OB,GC=GB,
∴BC⊥OD,且D为BC的中点,
∴∠BAC,
∵,
∴,,
①当BC为底边,点A在弦BC所对的优弧上时,AC=AB,
∴BC=2CD,AD⊥BC,
∵OC=OB,
∴∠COGCOB,
∵∠CABCOB,
∴∠COG=∠CAB,
∴BC=2CD=2 r sin∠COG=2 r sin∠BAC=6,
连接OA,∵AC=AB,
∴A,O,D,G四点共线,
∴,
∴;
②当AB为底边时,AC=BC,
∴AB⊥OC于点F,
令CF=3t,则,
∵OF2+BF2=OB2,
即(r﹣3t)2+(4t)2=r2
解得,
∴,,
过点G作AB的垂线,垂足为点H,
∵AB⊥OC,CG⊥OC,
∴四边形CFHG为矩形,
∴AH=HF+FA=CG+BF=rtan∠COG+BF=rtan∠BAC+BFrr,,
∴,
由①知BC=2CD=2 r sin∠BACr,
∴;
③当AC为底边时,由对称性,与AB为底边时的情况相同.
综上所述,或;
(3)解:延长AC,BG交于点D,
∵∠CGD=180°﹣∠BGC=2∠A,∠D=90°﹣∠A,
∴∠D=∠DCG,
∴CG=DG,
由(1)得CG=GB,
∴GB=DG,G是BD的中点,
∵GM⊥GB,AB⊥GB,
∴GM∥AB,M是AD的中点.
连接OM,则四边形OMGB为矩形,
∴OM=GB,
∴OB2=OA2=AM2﹣OM2=AM2﹣GB2,
设GB=x,AM=y,则0<x<2,
∵AM2+OB2﹣3GB2+8GB﹣8=0,
∴OB2=y2﹣x2=x2﹣4x+4=(x﹣2)2,
∴S四边形MGBA=3S△AOM=3xx2+3x(x﹣1)2,
∴当x=1时,四边形MGBA的面积最大为.
7.【解答】(1)证明:连接OC,
∵CD是⊙O的切线,
∴OC⊥DE,
∵DE⊥BE,
∴OC∥BE,
∴∠EBC=∠OCB,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC=∠EBC,
∴BC平分∠DBE.
(2)证明:连接AC,
∵AB是直径,
∴∠ACB=90°,
∵BE⊥CD,
∴∠BED=90°,
∴△ABC∽△CBE,
∴,
∴BC2=AB BE.
(3)解:设⊙O的半径为r,
∵,
∴,
∴,
∴,
∵∠DCO=90°,∠BED=90°,
∴△DCO∽△DEB,
∴,即,
∴,
∵AB BE=80,
∴,
∴r1=5,r2=﹣5(舍去),
∴⊙O的半径为5.
8.【解答】解:(1)连接OD,如图:
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COD=2∠A,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠C+∠COD=90°,即∠C+2∠A=90°,
又∵DA=DC,
∴∠A=∠C,
∴∠C=30°;
(2)①连接AF,OF,如图:
∵AB是直径,
∴∠AFB=90°,
∵tan∠FBA=1,
∴∠FBA=45°,
∴△ABF为等腰直角三角形,
∴AF=BF=5,OF⊥AB,
∵PF∥AD,
∴∠FPO=∠DAC=∠C=30°,
∴PF=2OF=10,OPOF=5,
∴BP=OP﹣OB=55,
∵∠FAB+∠FEB=180°,∠PEB+∠FEB=180°,
∴∠FAB=∠PEB,
又∵∠EPB=∠APF,
∴△AFP∽△EBP,
∴,
∴BE();
②过点B作BG⊥FP于G,连接OE,过O作ON⊥EF于N,如图:
∴∠BGE=∠BGP=90°,
∴∠BGE=∠AFB,
∵∠BEP=∠FAP,
∴△PEB∽△PAF,
∴,
∴BP AP=PE PF,
设BG=x,
∵∠FPA=∠DAC=30°,
∴BP=2x,PGx,
∴AP=10+2x,OP=5+2x,
∴ONOPx,PN(5+2x),
在Rt△NOE中,EN2=OE2﹣ON2=25﹣(x)2,
∵ON⊥EF,
∴FN=EN,EF=2EN,
在Rt△EBG中,BE2=BG2+EG2,
在Rt△BFG中,BF2=BG2+FG2,
∵FG=PN+FN﹣PG,EG=PN﹣PG﹣FN,
∴FG EG=(PN﹣PG)2﹣FN2[25﹣(x)2]=x2+5x,FG+EG=2(PN﹣PG)=5,
∴BE2 BF2=(BG2+EG2)(BG2+FG2)
=BG4+(EG2+FG2)BG2+(EG FG)2
=BG4+[(EG+FG)2﹣2EG FG]BG2+(EG FG)2
=x4+[75﹣2x2﹣10x]x2+(x2+5x)2
=100x2,
∴BE BF=10x,
∵,
∴BE BF=EF2=4EN2,
即10x=4[25﹣(x)2],
解得:x(舍去)或,
∴BP=2x.
9.【解答】解:(1)∵M为AB中点,AB=20,
∴,
∵DM⊥AB,
在Rt△ADM中,即:,
∴;
(2)连接CM,
∵M是Rt△ABC斜边上的中点,
∴,
∴∠A=∠ACM,∠B=∠BCM,
∵∠MPQ=∠ACM,
∴∠A=∠MPQ,
∵QP是⊙O的直径,
∴∠ACB=∠PMQ=90°,
∴∠PQM=∠ABC=∠BCM,
∵,
∴,
∵;
∴;
(3)∵∠QMA+∠QMD=90°,∠DMP+∠QMD=90°,
∴∠QMA=∠DMP,
由(1)知∠A=∠MPQ.
∴△AMO∽△PME,
当△PME是等腰三角形时,有△AMQ为等腰三角形,
当AM=AQ时,AQ=10,
当AM=MQ时,∠A=∠AQM=∠ACM,而∠AQM>∠ACM,所以这种情况不存在;
当AQ=MQ时,∠A=∠QMA,
而∠A+∠ADM=90°,∠QMA+∠DMQ=90°,
∴∠ADM=∠DMQ,
∴,
由(1)知,可得;
∴AQ=10或.
10.【解答】(1)解:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC=90°﹣∠A=55°,
∵BD与⊙O相切于点B,
∴BD⊥AB,
∴∠DBC=90°﹣∠ABC=35°,
(2)证明:∵OA=OC,
∴∠A=∠ACO,又∠ACO=∠DCE,
∴∠DCE=∠A=∠DBC,
又∵∠D=∠D,
∴△DCE∽△DBC,
∴,
∴CE BD=BC CD;
(3)解:∵AB=8,
∴,
,
,
∴DC=OD﹣OC=6﹣4=2,,
∵∠DBC=∠DCE,∠D=∠D,
∴△DBC∽△DCE,
,
,
,
∴BE的长是.
11.【解答】(1)证明:连接OB,
∵PB是⊙O的切线,
∴∠PBO=90°,
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB,
又∵PO=PO,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO=90°,
∵OA为圆的半径,
∴直线PA为⊙O的切线;
(2)证明:∵∠PAO=∠PDA=90°,
∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°,
∴∠OAD=∠OPA,
∴△OAD∽△OPA,
∴,
∴OA2=OD OP,
又∵AC=2OA,
∴AC2=4OD OP;
(3)解:∵OA=OC,AD=BD,BC=6,
∴ODBC=3,
设AD=x,
∵tan∠F,
∴FD=2x,OA=OF=2x﹣3,
在Rt△AOD中,由勾股定理,得,
(2x﹣3)2=x2+32,
解之得,x1=4,x2=0(不合题意,舍去),
∴AD=4,OA=2x﹣3=5,
∵AC是⊙O的直径,
∴AC=2OA=10.
∴AC的长为10.
12.【解答】解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=∠ADB=90°;
(2)连接OD,
∵∠P=∠PDB,
∴BD=BP=3,
∵PD是⊙O的切线,
∴OD⊥PD,
∴∠ODB+∠PDB=90°,∠P+∠POD=90°,
∵∠P=∠PDB,
∴BO=BD=3,
∴OB=BD=OD,
∴△OBD是等边三角形,
∴∠DOB=60°,
∴弧BD的长度π,
在Rt△CDB中,BD=3,∠CBD=30°,
∴CD,BC=2,
∴阴影部分的周长为π+3;
(3)连接OM,过点D作DF⊥AB交于点F,
∵AM=BM,
∴OM⊥AB,
∵,
∴∠DMB=∠DAB,
∴tan∠DMB=tan∠DAB,
∵tan∠DMB,
∴tan∠DAB
设BD=a,则AD=2a,
∴ABa,
∴OMa,
∵AD BD=AB DF,
∴DFa,
∵DF⊥AB,OM⊥AB,
∴OM∥DF,
∴△OMN∽△FDN,
∴,
∴,
∴MN:MD.
13.【解答】解:(1)证明:如图,连接OE,
∵GF=GE,∴∠GFE=∠GEF=∠AFH,
∵OA=OE,∴∠OAE=∠OEA,
∵∠AFH+∠FAH=90°,
∴∠GEF+∠AEO=90°,
∴∠GEO=90°,∴GE⊥OE,
∴EG是⊙O的切线;
(2)连接DE,易得△GDE∽△GEC,
∴,
∴GE2=GC GD,
又∵GF=GE,
∴GF2=GC GD;
(3)如图,连接OC.
设⊙O的半径为r.
在Rt△AHC中,
,
∵,
∴,
在Rt△HOC中,
∵OC=r,,,
∴,
∴,
∵GM∥AC,
∴∠CAH=∠M,
∵∠OEM=∠AHC,
∴△AHC∽△MEO,
∴,
∴,
∴.
14.【解答】(1)证明:连接OB,如图,
∵AC为⊙O的直径,
∴∠ABC=90°.
∵,
∴BA=BC,
∴△ABC是等腰直角三角形,
∴∠BAC=∠BCA=45°.
∵OB=OC,
∠OBC=∠OCB=45°.
∵∠CBM=∠BAC,
∴∠CBM=45°,
∴∠OBM=∠CBM+∠CBO=90°,
∴BM⊥OB.
∵OB为⊙O的半径,
∴BM为⊙O的切线;
(2)解:①如解图②,作BG⊥CD于点G,BH⊥DA交DA的延长线于点H,如图,
∵BG⊥CD,BH⊥DH,
∴∠BHD=∠BGD=90°.
∵AC 为⊙O的直径,
∴∠ADC=90°,
∴四边形BGDH为矩形,
∵
∴BA=BC,∠ADB=∠BDC.
∵BG⊥CD,BH⊥DH,
∴BH=BG,
∴矩形BGDH为正方形,
在Rt△ABH和Rt△CBG中,
,
∴Rt△ABH≌Rt△CBG(HL),
∴S△ABH=S△CBC,
∴S四边形ABCD=S正方形BGDH,
∵BD2,
∴;
②由(1)知:∠PBC=∠BAC=45°.
∴∠PDB=∠BAC=∠PBC=45°,
∵∠BPC=∠DPB,
∴△BCP∽△DBP,
∴.
∵S△BCD:S△BCP=7:9,
∴,
∴,
∴.
在Rt△ABC中,
∵,
∴BD=3,
∴BD=4,
即 .
∴;
(3)线段FA,FB,FC能构成一个三角形,三角形的形状为直角三角形,证明如下:
如图,
∵,∠ABD=∠ACD,
∴.
由(2)①知:∠ADC=90°,
∴tan∠ACD,
∴.
∵E为CD的中点,
∴,
∴AD=ED,
∴△ADE是等腰直角三角形.
由(2)①知,∠ADB=∠BDC,
∴DB垂直平分AE,
∴,
∴,
∴,
∵∠CEF=∠AEC,
∴△CEF∽△AEC,
∴,
∴.
由(1)知:△ABC是等腰直角三角形,
∴,
∴FC=AB,
在Rt△ABF中,FA2+FB2=AB2,
∴FA2+FB2=FC2,
∴线段FA,FB,FC能构成一个直角三角形.
15.【解答】(1)证明:连接OD,如图,
∵DE为⊙O的切线,
∴OD⊥DE.
∵AB为直径,
∴∠ACB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠AOD=2∠ACD=90°,
∴OD⊥AB,
∴DE∥AB;
(2)解:∵DE∥AB,
∴∠E=∠ABC,
∵∠ABC=∠ADC,
∴∠E=∠ADC,
∵∠ECD=∠ACD,
∴△DCE∽△ACD,
∴,
∴CD2=CA CE.
∴当CD取得最大值时,CA CE的值最大,
∵CD是圆O的弦,
∴CD为直径时取得最大值,
∵⊙O的半径为1,
∴CD的最大值为2,
∴CA CE的最大值为4.
(3)解:设tan∠ABC=x,tan∠AEC=y,
∵AB为直径,
∴∠ACB=90°,
∴y=tan∠AEC.
由(2)知:,
∴y=tan∠AEC,
过点D作DF⊥CE于点F,如图,
设EF=a,
∵DE∥AB,
∴∠ABC=∠DEC,
∴tan∠DEC=tan∠ABC=x,
∴DF=EF tan∠DEC=ax,
∵∠DCE=45°,
∴CF=DF=ax,
∴CDDFax,CE=ax+a,
∴y,
∵,
∴,
∴:7:3,
∴x:y=7:3,
∴yx.
把yx代入y中,
∴,
解得:x1,x2,
当x时,y,
当x时,y.
∴tan∠AEC的值为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
