《矩形与菱形习题课》教学设计

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
《矩形与菱形习题课》教学设计
沭阳县建陵中学 仲伟东
教学目标：
1. 能熟练进行矩形的性质与判定的综合应用。
2. 能熟练进行菱形的性质与判定的综合应用。
3. 能正确掌握运用矩形与菱形的知识解决一些综合性问题和开放性问题的方法。
教学重、难点：
1. 矩形与菱形知识点的综合应用；
2. 开放性问题与探索性问题的思考方法。
教学过程：
一、矩形：
第一部分：
基础演练（引出知识点）
如图，已知矩形ABCD的一条对角线长是8cm,两条对角线AC、BD相交于点O,且∠AOB＝ 60°。
⑴矩形的边AB长为_______
⑵矩形的边BC长为 _______
⑶矩形ABCD的周长为_______
矩形的性质:（总结知识点）
(1)边:对边平行且相等;
(2)角: 矩形的四个角都是直角；
(3)对角线:矩形的对角线相等且互相平分；
⑷对称性：矩形既是轴对称图形，又是中心对称图形。
知识巩固：（应用知识点）
如图，在矩形ABCD中，∠BAD的平分线交BC于E,O为对角线的交点，且∠CAE＝15°。
⑴猜想：△AOB为何种三角形，请说明你的理由；
⑵求：∠AOE的度数。
第二部分：
请你判断（引出知识点）
一位很有名望的木工师傅，招收了两名徒弟。一天，师傅有事外出，两徒弟就自已在家练习用两块四边形的废料各做了一扇矩形式的门，完事之后，两人都说对方的门不是矩形，而自已的是矩形。
甲的理由是：“我用角尺量我的门任意三个角，发现它们都是直角。所以我这个四边形门就是矩形”
乙的理由是：“我用直尺量这个门的两条对角线，发现它们的长度相等，所以我这个四边形门就是矩形”。
根据它们的对话，你能肯定谁的门一定是矩形？
解：甲是正确的，因为有三个角是直角的四边形是矩形。乙不正确，因为对角线相等的四边形不一定是矩形，比如等腰梯形的对角线也相等。若要判断还要看四边形是否是平行四边形。
矩形的判定（总结知识点）
矩形判定方法1
有一个角是直角的平行四边形是矩形
矩形判定方法2
有三个角是直角的四边形是矩形。
矩形判定方法3
对角线相等的平行四边形是矩形。
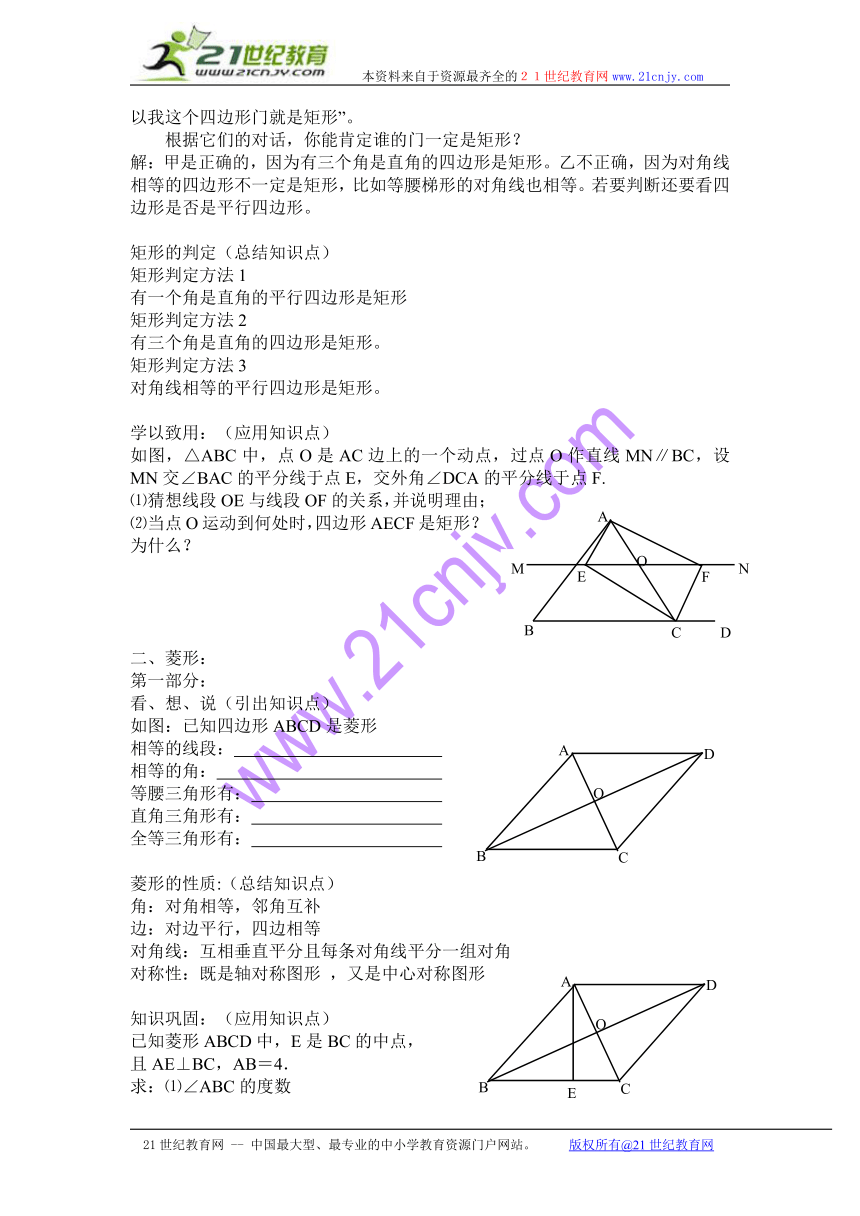
学以致用：（应用知识点）
如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BAC的平分线于点E，交外角∠DCA的平分线于点F.
⑴猜想线段OE与线段OF的关系，并说明理由；
⑵当点O运动到何处时，四边形AECF是矩形？为什么？
二、菱形：
第一部分：
看、想、说（引出知识点）
如图：已知四边形ABCD是菱形
相等的线段：
相等的角：
等腰三角形有：
直角三角形有：
全等三角形有：
菱形的性质:（总结知识点）
角：对角相等，邻角互补
边：对边平行，四边相等
对角线：互相垂直平分且每条对角线平分一组对角
对称性：既是轴对称图形 ，又是中心对称图形
知识巩固：（应用知识点）
已知菱形ABCD中，E是BC的中点，
且AE⊥BC，AB＝4．
求：⑴∠ABC的度数
⑵对角线AC的长
⑶菱形ABCD的面积
第二部分：
基础演练（引出知识点）
如图，在平行四边形ABCD中，AE、CF分别是∠BAD和∠BCD的平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是 （只写出一个即可，图中不能再添加别的“点”和“线” ）
菱形的判定（总结知识点）
菱形判定方法1
有一组邻边相等的平行四边形是矩形
矩形判定方法2
四边相等的四边形是矩形。
矩形判定方法3
对角线互相垂直的平行四边形是矩形。
请你做主：（应用知识点）
已知：如图，在△ABC中，D是AB边上的一点，且BD＝BC，BF⊥DC于点E，交AC于点F，请你添加一个条件，使四边形DMCF是菱形，并说明理由。
三、综合：
赏析例一:
如图，在矩形ABCD中，对角线AC、BD相交于点O，AB=3，AD=4，P是AD上的一个动点，PE⊥AC于E，PF⊥BD于F。试说明： PE＋ PF的结果是一个定值并求出这个定值。
探索应用:
如图，已知菱形ABCD的周长是16厘米，E是BC边的中点，∠BAD=1200，如果P是BD上的一个动点，问当点P在什么位置时PE＋PC有最小值？并求出这个最小值。
赏析例二:
如图，过四边形ABCD的四个顶点分别作对角线AC、BD的平行线，所围成的四边形EFGH显然是平行四边形。
⑴当四边形ABCD分别是菱形、矩形、等腰梯形时，相应的平行四边形EFGH一定是“菱形、矩形”中的哪一种？请将你的结论填入下表：
四边形ABCD 菱形 矩形 等腰梯形
平行四边形EFGH
⑵反之，当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时，相应的原四边形ABCD必须满足怎样的条件？
探索应用:
如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形： △ABD、△BCE 、△ACF，请探索下列问题：
⑴四边形ADEF是什么四边形？为什么？
⑵当△ABC满足什么条件时，四边形ADEF是矩形？
⑶当△ABC满足什么条件时，四边形ADEF是菱形？
⑷当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在？
小结与作业：
课堂小结
1. 矩形、菱形的性质与判定的理解与应用；
2. 综合性与开放性较强习题的思考方法与解题技巧。
作业布置
完成课本109页第14题、第15题；
预习正方形。
D
C
B
A
O
E
B
C
D
A
O
F
E
M
N
D
C
B
A
O
C
D
B
A
O
E
C
D
B
A
O
E
F
D
C
B
A
O
E
F
M
C
B
D
A
O
P
E
F
D
C
A
B
E
P
C
D
A
B
H
G
F
E
D
A
B
C
E
D
C
B
A
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网