期中考试真题分类汇编04 单项选择(含答案+解析)---2024-2025学年北师大版五年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编04 单项选择(含答案+解析)---2024-2025学年北师大版五年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 462.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 08:13:10 | ||
图片预览




文档简介
2024-2025学年北师大版五年级数学下册
期中考试真题分类汇编04 单项选择
一、单选题
1.(2024五下·威县期中)1千克棉花的和3千克铁的相比较,( )重。
A.1千克棉花的 B.3千克铁的 C.一样
2.(2024五下·瑞安期中)甲、乙两个长方体的长、宽、高如右图所示,甲长方体的体积是乙长方体体积的( )倍。
A.2 B.4 C.8 D.9
3.(2024五下·威县期中)若 (a和b都大于0) , 则下列说法正确的是( )。
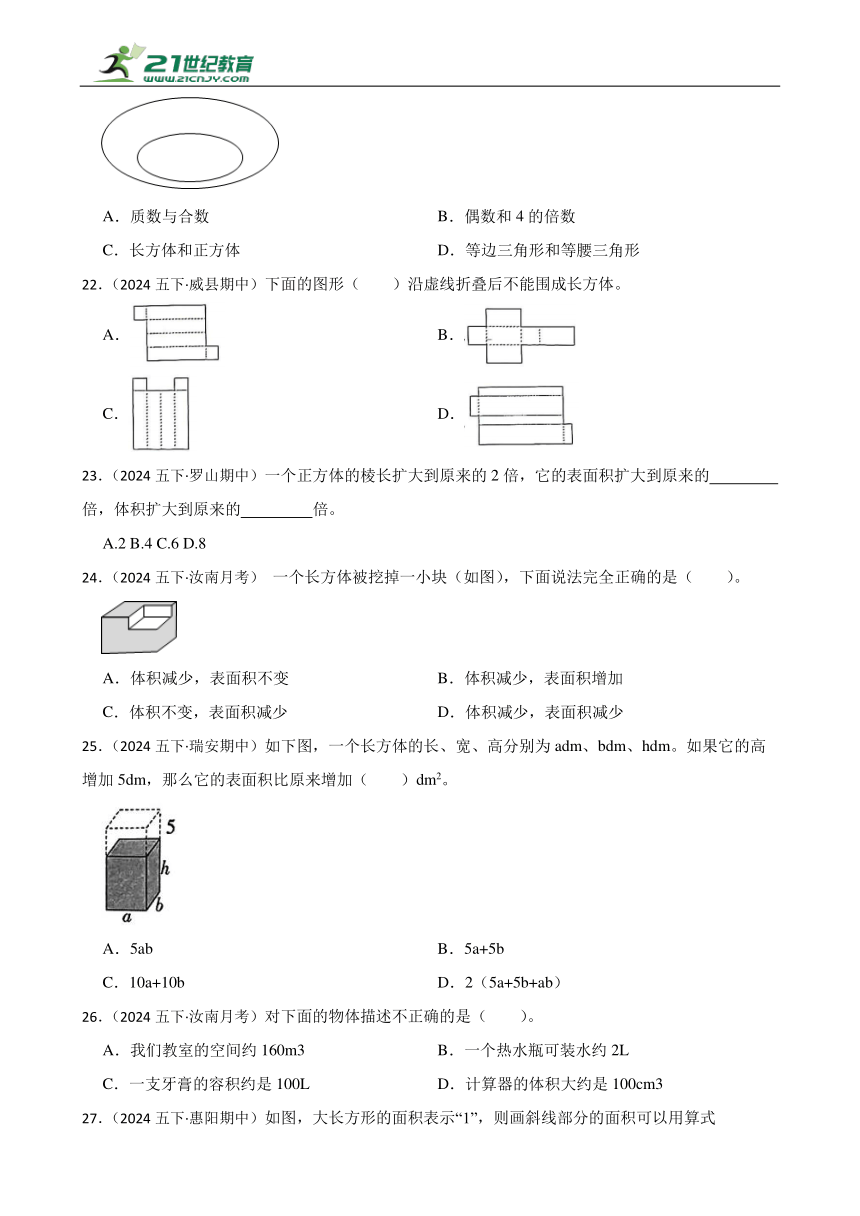
A.a>b B.a=b C.a4.(2024五下·瑞安期中)将一个大长方体切分成两个完全一样的小长方体,按下图所示的三种切法,表面积分别增加50cm2、40cm2、90cm2。原来大长方体的表面积是( )cm3。
A.180 B.90 C.360 D.390
5.(2024五下·期中)一根方木的体积是80 cm3,长是20cm,这根方木的横截面积是( )。
A.4 cm B.4cm2 C.4 cm3
6.(2024五下·瑞安期中)如下图,有一个无盖的正方体纸盒,下底标有字母“M”,将其剪开展成平面图形,想一想,这个平面图形是( )。
A. B.
C. D.
7.(2024五下·瑞安期中)求“一个水壶能装多少水 ”就是求这个水壶的( )。
A.体积 B.容积 C.表面积 D.质量
8.(2024五下·期中)一条水渠长km,第一周修了它的,第二周修了km。两周修的长度相比,( )。
A.第一周更长 B.第二周更长 C.一样长
9.(2024五下·瑞安期中)右下面的正方体都是用棱长1cm的小正方体摆成的。从边角拿走一个小正方体后(如右图),下列说法中,( )是正确的。
A.表面积不变,体积不变 B.表面积不变,体积减少
C.表面积增加,体积减少 D.表面积减少,体积减少
10.(2024五下·瑞安期中)下面第( )幅图是正方体的展开图。
A. B. C. D.
11.(2024五下·瑞安期中)求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的( )。
A.底面积 B.表面积 C.容积 D.体积
12.(2024五下·北仑期中)一个长方体长a厘米.宽b厘米,高c厘米,如果它的长增加2厘米,那么它的表面积比原来增加( )平方厘米。
A.4b+4c B.2bc C.4bc D.2b+2c
13.(2024五下·北仑期中)下面的说法中,正确的有( )个。
①把一根长14cm的彩带剪成两段(每段长度都是整厘米数),肯定两段都是偶数。
②a、b、c是三个不同的自然数,若a是b的倍数,b是c的倍数,则a是c的倍数。
③既是3的倍数,又是5的倍数的数一定是奇数。
④两个长方体的表面积相等,它们的长、宽、高一定也相等。
⑤面积单位间的进率是100,体积单位间的进率是1000。
A.①②③④⑤ B.①②③④ C.② D.②③
14.(2024五下·北仑期中)将四个长10cm,宽5cm、高3cm的礼盒用彩纸全部包住,下列包装方式最省彩纸的是( )。
A. B. C. D.
15.(2024五下·北仑期中)一个长方体玻璃容器,长8dm,宽6dm,高4dm,容器内有3.5dm深的水,现在放入一个棱长为3dm的正方体铁块,铁块沉入水中,此时容器中( )。
A.水将溢出27L
B.水将溢出3L
C.水面上升0.3dm
D.水面与容器恰好持平,水未溢出
16.(2024五下·惠阳期中)小明用正方体搭成一个长方体,被妹妹拿走了一块,长方体的表面积( )。
A.不变 B.变大 C.变小 D.无法确定
17.(2024五下·北仑期中)李阿姨在雕刻时先对材料进行了处理。她把一块长7dm、宽6dm、高5dm的长方体木块削成一个最大的正方体,在剩下部分中再削一个正方体,则这个正方体的的体积是( )dm3。
A.1 B.2 C.4 D.8
18.(2024五下·北仑期中)棱长之和相等的长方体和正方体,( )。
A.长方体的体积大 B.正方体的体积大
C.它们的体积相等 D.长方体的表面积大
19.(2024五下·北仑期中)大正方体的表面积是小正方体的表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的( )倍。
A.2 B.4 C.6 D.8
20.(2024五下·北仑期中)将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是( )。
A.0.02L B.0.2L C.2L D.0.002L
21.(2024五下·汝南月考)下面各组中两者之间关系不适合用下图表示的是( )。
A.质数与合数 B.偶数和4的倍数
C.长方体和正方体 D.等边三角形和等腰三角形
22.(2024五下·威县期中)下面的图形( )沿虚线折叠后不能围成长方体。
A. B.
C. D.
23.(2024五下·罗山期中)一个正方体的棱长扩大到原来的2倍,它的表面积扩大到原来的 倍,体积扩大到原来的 倍。
A.2 B.4 C.6 D.8
24.(2024五下·汝南月考) 一个长方体被挖掉一小块(如图),下面说法完全正确的是( )。
A.体积减少,表面积不变 B.体积减少,表面积增加
C.体积不变,表面积减少 D.体积减少,表面积减少
25.(2024五下·瑞安期中)如下图,一个长方体的长、宽、高分别为adm、bdm、hdm。如果它的高增加5dm,那么它的表面积比原来增加( )dm2。
A.5ab B.5a+5b
C.10a+10b D.2(5a+5b+ab)
26.(2024五下·汝南月考)对下面的物体描述不正确的是( )。
A.我们教室的空间约160m3 B.一个热水瓶可装水约2L
C.一支牙膏的容积约是100L D.计算器的体积大约是100cm3
27.(2024五下·惠阳期中)如图,大长方形的面积表示“1”,则画斜线部分的面积可以用算式( )表示。
A.× B.× C.× D.×
28.(2024五下·徐州鼓楼期中)甲乙两筐苹果,甲筐32千克,乙筐x千克。从甲筐拿4千克放入乙筐,两筐苹果就一样重。下列方程正确的是( )。
A.32-x=4 B.x-8=32 C.x+4=32-4
29.(2024五下·瑞安期中)下列说法中,错误的是( )。
A.一个正方体的棱长是6cm,它的体积和表面积相等。
B.两个正方体木块的表面积相等,它们的体积也一定相等。
C.长、宽、高都相等的长方体一定是正方体。
D.在长方体中,相对的两个面有可能是正方形。
30.(2024五下·罗山期中)用一根长( )cm的铁丝正好可以做成一个长 4cm、宽5cm、高7cm 的长方体框架。
A.32 B.140 C.64 D.128
31.(2024五下·罗山期中)下列图形中,能折成正方体的有( )个。
A.1 B.2 C.3 D.4
32.(2024五下·惠阳期中)下列四个图形中,不能拼成正方体的是( )。
A. B.
C. D.
33.(2024五下·期中)如果 >(b≠0),那么( )。
A.a>b B.a34.(2024五下·期中) 用同样的小正方体拼成一个较大的正方体,至少需要( )个小正方体。
A.4 B.8 C.10
35.(2024五下·期中)至少还需要( )个这样的小正方体才能将右边的几何体堆成一个大正方体。
A.4 B.6 C.7
36.(2024五下·期中) 在同一个长方体中,至少有( )条棱长是相等的。
A.2 B.4 C.6
37.(2024五下·期中)药房打算把两种不同的常规药上半年的销售变化情况绘制成统计图,选择( )统计图最合适。
A.单式条形 B.单式折线 C.复式条形 D.复式折线
38.一个棱长为8cm的正方体,计算它的表面积,算式为( )。
A.8×12 B.8×8×6 C.8×8×8
39.(2024五下·期中)一根钢管,它的横截面面积是20平方厘米,把它截成4段,表面积增加了( )。
A. B. C. D.
40.(2024五下·期中)把一个棱长9cm的正方体,切割成棱长3cm的小正方体,可以切成( )块。
A.9 B.18 C.27
41.(2024五下·期中)下列沿虚线折叠后不能围成正方体的是( )。
A.
B.
C.
42.(2024五下·期中)一根长 米,用去全长的 ,还剩( )米。
A. B. C.
43.(2024五下·期中)下面算式的积在和之间的是( )。
A. B. C.
44.(2024五下·松桃期中)下面的平面图中,( )不能折成正方体。
A. B. C.
45.(2024五下·松桃期中)俊俊渴极了,一次喝了( )水。
A.500毫升 B.5升 C.1立方米
46.(2024·期中)小雨用棱长1 cm的小正方体搭了一个3×3×3的大正方体(如图),这时小乐走过来,他出了个问题考小雨:“如果我从最上层拿走一个小正方体,表面积会怎么变?”请你帮小雨选一下,以下选项不可能的是( )。
A.表面积与原来一样 B.表面积比原来增加2 cm2
C.表面积比原来增加3 cm2 D.表面积比原来增加 4 cm2
47.(2024·期中)一个长方体的长、宽、高分别是a米、b米、h米,如果高增加2米,那么新的长方体的体积比原来增加 ( )立方米。
A.ab(h+2) B.2ab C.2(2a+26) D.2abh
48.(2024·期中)下面可以折成正方体的图形是 ( ) 。
A. B. C.
49.下面不是正方体展开图的是( )。
A. B.
C. D.
50.(2024五下·期中)如图,把它折成一个正方体(数字编号要折在外面),若从前面看到的是⑥,从右面看到的是②,则从上面看到的是( )。
A.① B.③ C.④ D.⑤
答案解析部分
1.C
解:1×=(千克)
3×=(千克)
=,质量相等。
故答案为:C。
求一个数的几分之几是多少,用乘法计算,然后比较大小。
2.B
解:6×3×4=72
3×3×2=18
72÷18=4。
故答案为:B。
长方体相交于一个顶点的三条棱,叫做长方体的长、宽、高,甲长方体的体积是乙长方体体积的倍数=(甲的长×甲的宽×甲的高) ÷(乙的长×乙的宽×乙的高)。
3.C
解: ,因为>,所以a<b。
故答案为:C。
两个数相乘的积相等,较小的数要乘较大的数。
4.A
解:50÷2=25(平方厘米),25=5×5
40÷2=20(平方厘米),20=5×4
90÷2=45(平方厘米),45=5×9
(45+25+20)×2
=90×2
=180(平方厘米)。
故答案为:A。
原来大长方体的表面积=三个面增加的表面积一半的和×2。
5.B
解:80÷20=4(平方厘米)。
故答案为:B。
这根方木的横截面积=体积÷底面积。
6.A
解:要使“M”是底面,这个平面图形是 。
故答案为:A。
要使“M”是底面,这个平面图形底面“M”不能与4个正方形一排,要单独一个。
7.B
解:求“一个水壶能装多少水 ”就是求这个水壶的容积。
故答案为:B。
容器所能容纳物体的体积就是它的容积。
8.C
解:×=(千米),=,两周修的一样长。
故答案为:C。
第一周修的长度=这条水渠的总长度×第一周修的分率,然后和第二周修的长度比较大小。
9.B
解:1×1×1=1(立方厘米), 表面积不变,体积减少 。
故答案为:B。
从边角拿走一个小正方体后,大正方体少了3个小正方体的面,又增加了3个小正方体的面,表面积不变,体积减少了1个小正方体的体积。
10.B
解:这个正方体展开图中圆点的面与涂色正方形的面是相邻的面,即 。
故答案为:D。
正方体相对的面不相邻,据此判断。
11.B
解:求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的表面积。
故答案为:B。
求这个纸箱的表面积,就是求至少需要纸板的面积。
12.A
解:(2c+2b)×2=(4b+4c)(平方厘米)。
故答案为:A。
增加的表面积=(高×增加的长+宽×增加的长)×2。
13.C
解:①14-1=13(厘米),两段都是奇数,原题干说法错误;
② a、b、c是三个不同的自然数,若a是b的倍数,b是c的倍数,则a是c的倍数 ,原题干说法正确;
③如90既是3的倍数,又是5的倍数,还是偶数,原题干说法错误;
④两个长方体的表面积相等,它们的长、宽、高不一定也相等,原题干说法错误;
⑤每相邻两个面积单位间的进率是100,每相邻两个体积单位间的进率是1000,原题干说法错误。
故答案为:C。
①奇数+奇数=偶数,偶数+偶数=偶数,两段都是奇数或者都是偶数;
②a、b、c是三个不同的自然数,同时是两个数倍数的一个数,较大的数是较小数的倍数;
③个位上是0或5,并且各个数位上的数的和是3的倍数,这个数同时是3和5的倍数;既是3的倍数,又是5的倍数的数可能是奇数或者偶数;
④长方体的表面积=(长×宽+长×高+宽×高)×2,两个长方体的表面积相等,它们的长、宽、高不一定也相等;
⑤每相邻两个面积单位间的进率是100,每相邻两个体积单位间的进率是1000。
14.B
解:把最大的面叠放在一起最省彩纸,即 。
故答案为:B。
要最省彩纸,就要把最大的面叠放在一起。
15.B
解:3×3×3=27(立方分米)
8×6×(4-3.5)
=48×0.5
=24(立方分米)
27-24=3(立方分米)
3立方分米=3升。
故答案为:B。
正方体铁块的体积=棱长× 棱长× 棱长;长方体玻璃容器上面没有水的体积=长×宽×(高-水的高度),然后比较大小,27-24=3(立方分米),则水将溢出3升。
16.A
解:长方体的表面积比原来减少3个小正方体面的面积,增加了3个小正方体面的面积,所以表面积不变。
故答案为:A。
关键比较拿掉面的个数与增加面的个数。
17.D
解:7-5=2(分米)
2×2×2=8(立方分米)。
故答案为:D。
第一次削去正方体的棱长是5分米,第二次削去正方体的棱长是2分米,这个正方体的体积=棱长×棱长×棱长。
18.B
解:假设正方体的棱长为2厘米,长方体的长、宽、高分别为1厘米、1厘米、4厘米,
则它们的棱长之和都为24厘米,
正方体的体积为:
2×2×2=8(立方厘米),
长方体的体积为:
1×1×4=4(立方厘米),8>4,所以正方体的体积要大一些;
长方体的表面积为:
1×1×2+1×4×4
=2+16
=18(平方厘米)
正方体的表面积为:
2×2×6=24(平方厘米),18<24,所以正方体的表面积大。
故答案为:B 。
假设出正方体的棱长,长方体的长、宽、高,依据长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,分别计算后再比较大小。
19.B
解:16÷4=4。
故答案为:B。
正方体的表面积=棱长×棱长×6,正方体的棱长和=棱长×12;因为大正方体的表面积是小正方体的表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的16÷4=4倍。
20.B
解:将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是0.2升。
故答案为:B。
根据实际生活经验以及题干中的具体数据来选择。
21.A
解:A项:质数与合数不是相互包含的关系,不能用这个图表示;
B项:偶数包含4的倍数;
C项:正方体是特殊的长方体;
D项:等边三角形是特殊的等腰三角形。
故答案为:A。
质数与合数不是相互包含的关系,不能用这个图表示,其余各项有包含关系,可以用这个图表示。
22.C
解:A项:是长方体展开图的“1-4-1”型;
B项:是长方体展开图的“1-4-1”型;
C项:不是长方体的展开图;
D项:是长方体展开图的“1-4-1”型。
故答案为:C。
依据长方体的展开图类型判断是否能围成长方体。
23.B;D
解:2×2=4;
2×2×2=8。
故答案为:B;D。
正方体的表面积=棱长×棱长×6,正方体的棱长扩大到原来的2倍,它的表面积扩大到原来的2×2=4倍;正方体的体积=棱长×棱长×棱长,体积扩大到原来的2×2×2=8倍。
24.A
解:一个长方体被挖掉一小块后,体积减少了挖掉部分的体积,表面积不变。
故答案为:A。
物体所占空间的大小,叫做它的体积,一个长方体被挖掉一小块后,体积减少了挖掉部分的体积;表面积少了挖掉部分3个面的面积,又增加了同样3个面的面积,则表面积不变。
25.C
解:(5a+5b)×2=(10a+10b)(平方分米)。
故答案为:C。
它原来增加的表面积=增加的侧面4个面的面积=(长×增加的高+宽×增加的高)×2。
26.C
解: 一支牙膏的容积约是100毫升,不可能是100升,其余各项都正确。
故答案为:C。
根据实际生活经验以及题干中的具体数据来进行选择。
27.C
解:画斜线部分的面积可以用算式是× 。
故答案为:C。
×表示:把单位“1”平均分成5份,取其中的3份,然后把平均分成3份,取其中的2份。
28.C
解:A:正确的方程应该是32-x=4+4;
B:正确的方程应该是x+8=32;
C:此方程正确。
故答案为:C。
从甲筐拿4千克放入乙筐,两筐苹果就一样重,说明甲筐比乙筐多了8千克。等量关系:甲筐的质量-乙筐的质量=8千克,乙筐的质量+8千克=甲筐的质量,甲筐的质量-4千克=乙筐的质量+4千克。根据等量关系列方程即可。
29.A
解:A项:表面积和体积首先表示的意义不同,其次,所用的计量单位不同,最后计算公式不同,所以它们无法比较大小,原题干说法错误;
B项:两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等,原题干说法正确;
C项:长、宽、高都相等的长方体一定是正方体,原题干说法正确;
D项:在长方体中,相对的两个面有可能是正方形,原题干说法正确。
故答案为:A。
A项:正方体的表面积和体积无法比较大小;
B项:正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等;
C项:正方体的12条棱都相等;
D项:长方体的6个面都是长方形,特殊情况下,相对的两个面是正方形。
30.C
解:(4+5+7)×4
=16×4
=64(厘米)
故答案为:C。
铁丝的长度=(长方体框架的长+宽+高)×4。
31.C
解:图二是正方体展开图的“1-4-1”型、图三是正方体展开图的“3-3”型、图四是正方体展开图的“2-2-2”型,所以图一不能折成正方体,后面3个图形都能折成正方体。
故答案为:C。
依据正方体展开图的各种情况判断。
32.C
解:A项:是正方体展开图的“2-2-2”型;
B项:是正方体展开图的“1-4-1”型;
C项:不是正方体的展开图;
D项:是正方体展开图的“1-3-2”型。
故答案为:C。
依据正方体展开图的类型判断。
33.A
解:当>1时,>(b≠0), 则a>b。
故答案为:A。
一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。所以要使>(b≠0),就要>1,那么a>b。
34.B
解:2×2×2=8(个),至少需要8个小正方体。
故答案为:B。
用同样大小的正方体拼成一个较大的正方体,每条棱上至少需要2个小正方体,所以拼成这个大正方体至少需要的小正方体是8个。
35.C
解:4+3=7(个)。
故答案为:C。
至少还需要这样小正方体的个数=上面一层缺少的个数+下面一层缺少的个数。
36.B
解:在同一个长方体中,至少有4条棱长是相等的。
故答案为:B。
长方体有12条棱,相对的4个棱长相等。
37.D
解:选择复式折线统计图最合适。
故答案为:D。
“两种”决定用复式,“变化”决定用折线,据此解答。
38.B
解:一个棱长为8cm的正方体,计算它的表面积,算式为8×8×6;
故答案为:B,
正方体的表面积=棱长×棱长×6,依此列出算式即可求解。
39.C
解:(4-1)×2×20
=3×2×20
=6×20
=120(平方厘米)。
故答案为:C。
把一根钢管截成4段,增加了3×2=6个横截面的面积,增加的表面积=横截面的面积×增加面的个数。
40.C
解:(9×9×9)÷(3×3×3)
=729÷27
=27(块)
故答案为:C。
正方体的棱长×棱长×棱长=正方体的体积,大正方体的体积÷小正方体的体积=可以切的块数。
41.A
解:第一个图形沿虚线折叠后不能围成正方体。
故答案为:A。
正方体的展开图如下:
42.B
解:×=(米),还剩米。
故答案为:B。
用去全长的 ,还剩全长的;全长×剩下的长度占全长的分率=剩下的长度。
43.B
解:因为<1,所以×<, 算式的积不在和之间,
因为<1,所以×<, 算式的积在和之间 。
×3=2, 算式的积不在和之间。
故答案为:B。
一个非0数乘大于1的数,积大于这个数,乘小于1的数,积小于这个数;据此解答。
44.A
解: 不是正方体的展开图,不能折成正方体。
故答案为:A。
后面两项都是正方体展开图的“1+4+1”型,能能折成正方体。
45.A
解:俊俊渴极了,一次喝了 500毫升水。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行选择。
46.C
解:从大正方体四个顶点处任意拿走一个小正方体表面积与原来一样;任意拿走四条棱上中间位置的正方体表面积比原来增加2cm2;拿走正中间的小正方体表面积比原来增加4cm2;所以不可能的是表面积比原来增加3cm2。
故答案为:C。
如图,大正方体四个顶点位置的小正方体有三个外露面,拿走一个后,原位置仍然有三个一样的面,所以表面积不变;大正方体每条棱中间位置的小正方体有两个外露面,拿走一个后,原位置处有4个一样的面,比原来多了4-2=2个面,所以表面积增加了2个面的面积;大正方体正中间位置的小正方体只有一个外露面,拿走后原位置有5个一样的面,比原来多了5-1=4个面,所以表面积增加了4个面的面积,据此可以判断。
47.B
解: V 1= a × b × h
新的长方体的高度变为 : h + 2
V2 = a × b × ( h + 2 )
增加的量:V2 V 1
V 2 V 1 = a × b × ( h + 2 ) a × b × h
= a × b × h + a × b × 2 a × b × h
= a × b × 2
= 2 a b
故答案为:B
根据长方体的体积公式,增加的是一个长a 米、宽b米.高2米的长方体, 通过对比原始体积和增加高度后的体积,计算出体积的净增加量。
48.C
解:A.B折叠时有重合的面,C能折成完整的正方体。
故答案为:C
根据正方体的展开图折成正方体注意不要有重合的面
49.C
解:A项:是正方体展开图的“1+4+1”型;
B项:是正方体展开图的“1+4+1”型;
C项:不是正方体的展开图;
D项:是正方体展开图的“1+4+1”型。
故答案为:C。
依据正方体展开图的各种型号判断。
50.D
解:把它折成一个正方体(数字编号要折在外面,若从前面看到的是⑥,从右面看到的是②,则从上面看到的是⑤。
故答案为:D。
根据正方体展开图的特征及看图可知,折成正方体后,①与⑥相对,②与④相对,③与⑤相对。折成正方体后,如果从前面看到的是⑥,那么后面就是①,从右面看到的是②,那么从左面看到的就是④,则从上面看到的就是⑤,从下面看到的是③。
期中考试真题分类汇编04 单项选择
一、单选题
1.(2024五下·威县期中)1千克棉花的和3千克铁的相比较,( )重。
A.1千克棉花的 B.3千克铁的 C.一样
2.(2024五下·瑞安期中)甲、乙两个长方体的长、宽、高如右图所示,甲长方体的体积是乙长方体体积的( )倍。
A.2 B.4 C.8 D.9
3.(2024五下·威县期中)若 (a和b都大于0) , 则下列说法正确的是( )。
A.a>b B.a=b C.a4.(2024五下·瑞安期中)将一个大长方体切分成两个完全一样的小长方体,按下图所示的三种切法,表面积分别增加50cm2、40cm2、90cm2。原来大长方体的表面积是( )cm3。
A.180 B.90 C.360 D.390
5.(2024五下·期中)一根方木的体积是80 cm3,长是20cm,这根方木的横截面积是( )。
A.4 cm B.4cm2 C.4 cm3
6.(2024五下·瑞安期中)如下图,有一个无盖的正方体纸盒,下底标有字母“M”,将其剪开展成平面图形,想一想,这个平面图形是( )。
A. B.
C. D.
7.(2024五下·瑞安期中)求“一个水壶能装多少水 ”就是求这个水壶的( )。
A.体积 B.容积 C.表面积 D.质量
8.(2024五下·期中)一条水渠长km,第一周修了它的,第二周修了km。两周修的长度相比,( )。
A.第一周更长 B.第二周更长 C.一样长
9.(2024五下·瑞安期中)右下面的正方体都是用棱长1cm的小正方体摆成的。从边角拿走一个小正方体后(如右图),下列说法中,( )是正确的。
A.表面积不变,体积不变 B.表面积不变,体积减少
C.表面积增加,体积减少 D.表面积减少,体积减少
10.(2024五下·瑞安期中)下面第( )幅图是正方体的展开图。
A. B. C. D.
11.(2024五下·瑞安期中)求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的( )。
A.底面积 B.表面积 C.容积 D.体积
12.(2024五下·北仑期中)一个长方体长a厘米.宽b厘米,高c厘米,如果它的长增加2厘米,那么它的表面积比原来增加( )平方厘米。
A.4b+4c B.2bc C.4bc D.2b+2c
13.(2024五下·北仑期中)下面的说法中,正确的有( )个。
①把一根长14cm的彩带剪成两段(每段长度都是整厘米数),肯定两段都是偶数。
②a、b、c是三个不同的自然数,若a是b的倍数,b是c的倍数,则a是c的倍数。
③既是3的倍数,又是5的倍数的数一定是奇数。
④两个长方体的表面积相等,它们的长、宽、高一定也相等。
⑤面积单位间的进率是100,体积单位间的进率是1000。
A.①②③④⑤ B.①②③④ C.② D.②③
14.(2024五下·北仑期中)将四个长10cm,宽5cm、高3cm的礼盒用彩纸全部包住,下列包装方式最省彩纸的是( )。
A. B. C. D.
15.(2024五下·北仑期中)一个长方体玻璃容器,长8dm,宽6dm,高4dm,容器内有3.5dm深的水,现在放入一个棱长为3dm的正方体铁块,铁块沉入水中,此时容器中( )。
A.水将溢出27L
B.水将溢出3L
C.水面上升0.3dm
D.水面与容器恰好持平,水未溢出
16.(2024五下·惠阳期中)小明用正方体搭成一个长方体,被妹妹拿走了一块,长方体的表面积( )。
A.不变 B.变大 C.变小 D.无法确定
17.(2024五下·北仑期中)李阿姨在雕刻时先对材料进行了处理。她把一块长7dm、宽6dm、高5dm的长方体木块削成一个最大的正方体,在剩下部分中再削一个正方体,则这个正方体的的体积是( )dm3。
A.1 B.2 C.4 D.8
18.(2024五下·北仑期中)棱长之和相等的长方体和正方体,( )。
A.长方体的体积大 B.正方体的体积大
C.它们的体积相等 D.长方体的表面积大
19.(2024五下·北仑期中)大正方体的表面积是小正方体的表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的( )倍。
A.2 B.4 C.6 D.8
20.(2024五下·北仑期中)将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是( )。
A.0.02L B.0.2L C.2L D.0.002L
21.(2024五下·汝南月考)下面各组中两者之间关系不适合用下图表示的是( )。
A.质数与合数 B.偶数和4的倍数
C.长方体和正方体 D.等边三角形和等腰三角形
22.(2024五下·威县期中)下面的图形( )沿虚线折叠后不能围成长方体。
A. B.
C. D.
23.(2024五下·罗山期中)一个正方体的棱长扩大到原来的2倍,它的表面积扩大到原来的 倍,体积扩大到原来的 倍。
A.2 B.4 C.6 D.8
24.(2024五下·汝南月考) 一个长方体被挖掉一小块(如图),下面说法完全正确的是( )。
A.体积减少,表面积不变 B.体积减少,表面积增加
C.体积不变,表面积减少 D.体积减少,表面积减少
25.(2024五下·瑞安期中)如下图,一个长方体的长、宽、高分别为adm、bdm、hdm。如果它的高增加5dm,那么它的表面积比原来增加( )dm2。
A.5ab B.5a+5b
C.10a+10b D.2(5a+5b+ab)
26.(2024五下·汝南月考)对下面的物体描述不正确的是( )。
A.我们教室的空间约160m3 B.一个热水瓶可装水约2L
C.一支牙膏的容积约是100L D.计算器的体积大约是100cm3
27.(2024五下·惠阳期中)如图,大长方形的面积表示“1”,则画斜线部分的面积可以用算式( )表示。
A.× B.× C.× D.×
28.(2024五下·徐州鼓楼期中)甲乙两筐苹果,甲筐32千克,乙筐x千克。从甲筐拿4千克放入乙筐,两筐苹果就一样重。下列方程正确的是( )。
A.32-x=4 B.x-8=32 C.x+4=32-4
29.(2024五下·瑞安期中)下列说法中,错误的是( )。
A.一个正方体的棱长是6cm,它的体积和表面积相等。
B.两个正方体木块的表面积相等,它们的体积也一定相等。
C.长、宽、高都相等的长方体一定是正方体。
D.在长方体中,相对的两个面有可能是正方形。
30.(2024五下·罗山期中)用一根长( )cm的铁丝正好可以做成一个长 4cm、宽5cm、高7cm 的长方体框架。
A.32 B.140 C.64 D.128
31.(2024五下·罗山期中)下列图形中,能折成正方体的有( )个。
A.1 B.2 C.3 D.4
32.(2024五下·惠阳期中)下列四个图形中,不能拼成正方体的是( )。
A. B.
C. D.
33.(2024五下·期中)如果 >(b≠0),那么( )。
A.a>b B.a34.(2024五下·期中) 用同样的小正方体拼成一个较大的正方体,至少需要( )个小正方体。
A.4 B.8 C.10
35.(2024五下·期中)至少还需要( )个这样的小正方体才能将右边的几何体堆成一个大正方体。
A.4 B.6 C.7
36.(2024五下·期中) 在同一个长方体中,至少有( )条棱长是相等的。
A.2 B.4 C.6
37.(2024五下·期中)药房打算把两种不同的常规药上半年的销售变化情况绘制成统计图,选择( )统计图最合适。
A.单式条形 B.单式折线 C.复式条形 D.复式折线
38.一个棱长为8cm的正方体,计算它的表面积,算式为( )。
A.8×12 B.8×8×6 C.8×8×8
39.(2024五下·期中)一根钢管,它的横截面面积是20平方厘米,把它截成4段,表面积增加了( )。
A. B. C. D.
40.(2024五下·期中)把一个棱长9cm的正方体,切割成棱长3cm的小正方体,可以切成( )块。
A.9 B.18 C.27
41.(2024五下·期中)下列沿虚线折叠后不能围成正方体的是( )。
A.
B.
C.
42.(2024五下·期中)一根长 米,用去全长的 ,还剩( )米。
A. B. C.
43.(2024五下·期中)下面算式的积在和之间的是( )。
A. B. C.
44.(2024五下·松桃期中)下面的平面图中,( )不能折成正方体。
A. B. C.
45.(2024五下·松桃期中)俊俊渴极了,一次喝了( )水。
A.500毫升 B.5升 C.1立方米
46.(2024·期中)小雨用棱长1 cm的小正方体搭了一个3×3×3的大正方体(如图),这时小乐走过来,他出了个问题考小雨:“如果我从最上层拿走一个小正方体,表面积会怎么变?”请你帮小雨选一下,以下选项不可能的是( )。
A.表面积与原来一样 B.表面积比原来增加2 cm2
C.表面积比原来增加3 cm2 D.表面积比原来增加 4 cm2
47.(2024·期中)一个长方体的长、宽、高分别是a米、b米、h米,如果高增加2米,那么新的长方体的体积比原来增加 ( )立方米。
A.ab(h+2) B.2ab C.2(2a+26) D.2abh
48.(2024·期中)下面可以折成正方体的图形是 ( ) 。
A. B. C.
49.下面不是正方体展开图的是( )。
A. B.
C. D.
50.(2024五下·期中)如图,把它折成一个正方体(数字编号要折在外面),若从前面看到的是⑥,从右面看到的是②,则从上面看到的是( )。
A.① B.③ C.④ D.⑤
答案解析部分
1.C
解:1×=(千克)
3×=(千克)
=,质量相等。
故答案为:C。
求一个数的几分之几是多少,用乘法计算,然后比较大小。
2.B
解:6×3×4=72
3×3×2=18
72÷18=4。
故答案为:B。
长方体相交于一个顶点的三条棱,叫做长方体的长、宽、高,甲长方体的体积是乙长方体体积的倍数=(甲的长×甲的宽×甲的高) ÷(乙的长×乙的宽×乙的高)。
3.C
解: ,因为>,所以a<b。
故答案为:C。
两个数相乘的积相等,较小的数要乘较大的数。
4.A
解:50÷2=25(平方厘米),25=5×5
40÷2=20(平方厘米),20=5×4
90÷2=45(平方厘米),45=5×9
(45+25+20)×2
=90×2
=180(平方厘米)。
故答案为:A。
原来大长方体的表面积=三个面增加的表面积一半的和×2。
5.B
解:80÷20=4(平方厘米)。
故答案为:B。
这根方木的横截面积=体积÷底面积。
6.A
解:要使“M”是底面,这个平面图形是 。
故答案为:A。
要使“M”是底面,这个平面图形底面“M”不能与4个正方形一排,要单独一个。
7.B
解:求“一个水壶能装多少水 ”就是求这个水壶的容积。
故答案为:B。
容器所能容纳物体的体积就是它的容积。
8.C
解:×=(千米),=,两周修的一样长。
故答案为:C。
第一周修的长度=这条水渠的总长度×第一周修的分率,然后和第二周修的长度比较大小。
9.B
解:1×1×1=1(立方厘米), 表面积不变,体积减少 。
故答案为:B。
从边角拿走一个小正方体后,大正方体少了3个小正方体的面,又增加了3个小正方体的面,表面积不变,体积减少了1个小正方体的体积。
10.B
解:这个正方体展开图中圆点的面与涂色正方形的面是相邻的面,即 。
故答案为:D。
正方体相对的面不相邻,据此判断。
11.B
解:求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的表面积。
故答案为:B。
求这个纸箱的表面积,就是求至少需要纸板的面积。
12.A
解:(2c+2b)×2=(4b+4c)(平方厘米)。
故答案为:A。
增加的表面积=(高×增加的长+宽×增加的长)×2。
13.C
解:①14-1=13(厘米),两段都是奇数,原题干说法错误;
② a、b、c是三个不同的自然数,若a是b的倍数,b是c的倍数,则a是c的倍数 ,原题干说法正确;
③如90既是3的倍数,又是5的倍数,还是偶数,原题干说法错误;
④两个长方体的表面积相等,它们的长、宽、高不一定也相等,原题干说法错误;
⑤每相邻两个面积单位间的进率是100,每相邻两个体积单位间的进率是1000,原题干说法错误。
故答案为:C。
①奇数+奇数=偶数,偶数+偶数=偶数,两段都是奇数或者都是偶数;
②a、b、c是三个不同的自然数,同时是两个数倍数的一个数,较大的数是较小数的倍数;
③个位上是0或5,并且各个数位上的数的和是3的倍数,这个数同时是3和5的倍数;既是3的倍数,又是5的倍数的数可能是奇数或者偶数;
④长方体的表面积=(长×宽+长×高+宽×高)×2,两个长方体的表面积相等,它们的长、宽、高不一定也相等;
⑤每相邻两个面积单位间的进率是100,每相邻两个体积单位间的进率是1000。
14.B
解:把最大的面叠放在一起最省彩纸,即 。
故答案为:B。
要最省彩纸,就要把最大的面叠放在一起。
15.B
解:3×3×3=27(立方分米)
8×6×(4-3.5)
=48×0.5
=24(立方分米)
27-24=3(立方分米)
3立方分米=3升。
故答案为:B。
正方体铁块的体积=棱长× 棱长× 棱长;长方体玻璃容器上面没有水的体积=长×宽×(高-水的高度),然后比较大小,27-24=3(立方分米),则水将溢出3升。
16.A
解:长方体的表面积比原来减少3个小正方体面的面积,增加了3个小正方体面的面积,所以表面积不变。
故答案为:A。
关键比较拿掉面的个数与增加面的个数。
17.D
解:7-5=2(分米)
2×2×2=8(立方分米)。
故答案为:D。
第一次削去正方体的棱长是5分米,第二次削去正方体的棱长是2分米,这个正方体的体积=棱长×棱长×棱长。
18.B
解:假设正方体的棱长为2厘米,长方体的长、宽、高分别为1厘米、1厘米、4厘米,
则它们的棱长之和都为24厘米,
正方体的体积为:
2×2×2=8(立方厘米),
长方体的体积为:
1×1×4=4(立方厘米),8>4,所以正方体的体积要大一些;
长方体的表面积为:
1×1×2+1×4×4
=2+16
=18(平方厘米)
正方体的表面积为:
2×2×6=24(平方厘米),18<24,所以正方体的表面积大。
故答案为:B 。
假设出正方体的棱长,长方体的长、宽、高,依据长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,分别计算后再比较大小。
19.B
解:16÷4=4。
故答案为:B。
正方体的表面积=棱长×棱长×6,正方体的棱长和=棱长×12;因为大正方体的表面积是小正方体的表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的16÷4=4倍。
20.B
解:将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是0.2升。
故答案为:B。
根据实际生活经验以及题干中的具体数据来选择。
21.A
解:A项:质数与合数不是相互包含的关系,不能用这个图表示;
B项:偶数包含4的倍数;
C项:正方体是特殊的长方体;
D项:等边三角形是特殊的等腰三角形。
故答案为:A。
质数与合数不是相互包含的关系,不能用这个图表示,其余各项有包含关系,可以用这个图表示。
22.C
解:A项:是长方体展开图的“1-4-1”型;
B项:是长方体展开图的“1-4-1”型;
C项:不是长方体的展开图;
D项:是长方体展开图的“1-4-1”型。
故答案为:C。
依据长方体的展开图类型判断是否能围成长方体。
23.B;D
解:2×2=4;
2×2×2=8。
故答案为:B;D。
正方体的表面积=棱长×棱长×6,正方体的棱长扩大到原来的2倍,它的表面积扩大到原来的2×2=4倍;正方体的体积=棱长×棱长×棱长,体积扩大到原来的2×2×2=8倍。
24.A
解:一个长方体被挖掉一小块后,体积减少了挖掉部分的体积,表面积不变。
故答案为:A。
物体所占空间的大小,叫做它的体积,一个长方体被挖掉一小块后,体积减少了挖掉部分的体积;表面积少了挖掉部分3个面的面积,又增加了同样3个面的面积,则表面积不变。
25.C
解:(5a+5b)×2=(10a+10b)(平方分米)。
故答案为:C。
它原来增加的表面积=增加的侧面4个面的面积=(长×增加的高+宽×增加的高)×2。
26.C
解: 一支牙膏的容积约是100毫升,不可能是100升,其余各项都正确。
故答案为:C。
根据实际生活经验以及题干中的具体数据来进行选择。
27.C
解:画斜线部分的面积可以用算式是× 。
故答案为:C。
×表示:把单位“1”平均分成5份,取其中的3份,然后把平均分成3份,取其中的2份。
28.C
解:A:正确的方程应该是32-x=4+4;
B:正确的方程应该是x+8=32;
C:此方程正确。
故答案为:C。
从甲筐拿4千克放入乙筐,两筐苹果就一样重,说明甲筐比乙筐多了8千克。等量关系:甲筐的质量-乙筐的质量=8千克,乙筐的质量+8千克=甲筐的质量,甲筐的质量-4千克=乙筐的质量+4千克。根据等量关系列方程即可。
29.A
解:A项:表面积和体积首先表示的意义不同,其次,所用的计量单位不同,最后计算公式不同,所以它们无法比较大小,原题干说法错误;
B项:两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等,原题干说法正确;
C项:长、宽、高都相等的长方体一定是正方体,原题干说法正确;
D项:在长方体中,相对的两个面有可能是正方形,原题干说法正确。
故答案为:A。
A项:正方体的表面积和体积无法比较大小;
B项:正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等;
C项:正方体的12条棱都相等;
D项:长方体的6个面都是长方形,特殊情况下,相对的两个面是正方形。
30.C
解:(4+5+7)×4
=16×4
=64(厘米)
故答案为:C。
铁丝的长度=(长方体框架的长+宽+高)×4。
31.C
解:图二是正方体展开图的“1-4-1”型、图三是正方体展开图的“3-3”型、图四是正方体展开图的“2-2-2”型,所以图一不能折成正方体,后面3个图形都能折成正方体。
故答案为:C。
依据正方体展开图的各种情况判断。
32.C
解:A项:是正方体展开图的“2-2-2”型;
B项:是正方体展开图的“1-4-1”型;
C项:不是正方体的展开图;
D项:是正方体展开图的“1-3-2”型。
故答案为:C。
依据正方体展开图的类型判断。
33.A
解:当>1时,>(b≠0), 则a>b。
故答案为:A。
一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。所以要使>(b≠0),就要>1,那么a>b。
34.B
解:2×2×2=8(个),至少需要8个小正方体。
故答案为:B。
用同样大小的正方体拼成一个较大的正方体,每条棱上至少需要2个小正方体,所以拼成这个大正方体至少需要的小正方体是8个。
35.C
解:4+3=7(个)。
故答案为:C。
至少还需要这样小正方体的个数=上面一层缺少的个数+下面一层缺少的个数。
36.B
解:在同一个长方体中,至少有4条棱长是相等的。
故答案为:B。
长方体有12条棱,相对的4个棱长相等。
37.D
解:选择复式折线统计图最合适。
故答案为:D。
“两种”决定用复式,“变化”决定用折线,据此解答。
38.B
解:一个棱长为8cm的正方体,计算它的表面积,算式为8×8×6;
故答案为:B,
正方体的表面积=棱长×棱长×6,依此列出算式即可求解。
39.C
解:(4-1)×2×20
=3×2×20
=6×20
=120(平方厘米)。
故答案为:C。
把一根钢管截成4段,增加了3×2=6个横截面的面积,增加的表面积=横截面的面积×增加面的个数。
40.C
解:(9×9×9)÷(3×3×3)
=729÷27
=27(块)
故答案为:C。
正方体的棱长×棱长×棱长=正方体的体积,大正方体的体积÷小正方体的体积=可以切的块数。
41.A
解:第一个图形沿虚线折叠后不能围成正方体。
故答案为:A。
正方体的展开图如下:
42.B
解:×=(米),还剩米。
故答案为:B。
用去全长的 ,还剩全长的;全长×剩下的长度占全长的分率=剩下的长度。
43.B
解:因为<1,所以×<, 算式的积不在和之间,
因为<1,所以×<, 算式的积在和之间 。
×3=2, 算式的积不在和之间。
故答案为:B。
一个非0数乘大于1的数,积大于这个数,乘小于1的数,积小于这个数;据此解答。
44.A
解: 不是正方体的展开图,不能折成正方体。
故答案为:A。
后面两项都是正方体展开图的“1+4+1”型,能能折成正方体。
45.A
解:俊俊渴极了,一次喝了 500毫升水。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行选择。
46.C
解:从大正方体四个顶点处任意拿走一个小正方体表面积与原来一样;任意拿走四条棱上中间位置的正方体表面积比原来增加2cm2;拿走正中间的小正方体表面积比原来增加4cm2;所以不可能的是表面积比原来增加3cm2。
故答案为:C。
如图,大正方体四个顶点位置的小正方体有三个外露面,拿走一个后,原位置仍然有三个一样的面,所以表面积不变;大正方体每条棱中间位置的小正方体有两个外露面,拿走一个后,原位置处有4个一样的面,比原来多了4-2=2个面,所以表面积增加了2个面的面积;大正方体正中间位置的小正方体只有一个外露面,拿走后原位置有5个一样的面,比原来多了5-1=4个面,所以表面积增加了4个面的面积,据此可以判断。
47.B
解: V 1= a × b × h
新的长方体的高度变为 : h + 2
V2 = a × b × ( h + 2 )
增加的量:V2 V 1
V 2 V 1 = a × b × ( h + 2 ) a × b × h
= a × b × h + a × b × 2 a × b × h
= a × b × 2
= 2 a b
故答案为:B
根据长方体的体积公式,增加的是一个长a 米、宽b米.高2米的长方体, 通过对比原始体积和增加高度后的体积,计算出体积的净增加量。
48.C
解:A.B折叠时有重合的面,C能折成完整的正方体。
故答案为:C
根据正方体的展开图折成正方体注意不要有重合的面
49.C
解:A项:是正方体展开图的“1+4+1”型;
B项:是正方体展开图的“1+4+1”型;
C项:不是正方体的展开图;
D项:是正方体展开图的“1+4+1”型。
故答案为:C。
依据正方体展开图的各种型号判断。
50.D
解:把它折成一个正方体(数字编号要折在外面,若从前面看到的是⑥,从右面看到的是②,则从上面看到的是⑤。
故答案为:D。
根据正方体展开图的特征及看图可知,折成正方体后,①与⑥相对,②与④相对,③与⑤相对。折成正方体后,如果从前面看到的是⑥,那么后面就是①,从右面看到的是②,那么从左面看到的就是④,则从上面看到的就是⑤,从下面看到的是③。
同课章节目录
