期中考试真题分类汇编03 单项选择(含答案+解析)---2024-2025学年北师大版五年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编03 单项选择(含答案+解析)---2024-2025学年北师大版五年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 973.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 08:14:28 | ||
图片预览




文档简介
2024-2025学年北师大版五年级数学下册
期中考试真题分类汇编03 单项选择
一、单选题
1.(2024五下·高要期中)要制作12节长方体的铁皮通风管,每节长4分米,宽2分米,高0.5米(如右图所示),至少要用( )平方分米的铁皮。
A.48 B.672 C.720 D.912
2.(2024五下·潮南期中)一个长6dm,宽4dm,高5dm的长方体盒子,最多能放( )个2厘米的小正方体。
A.5 B.14 C.12
3.(2024五下·电白期中)正方体的棱长扩大到原来的3倍,体积扩大( )倍。
A.27 B.9 C.6 D.3
4.(2024五下·德江期中)下面现实情境中最适合提出与“体积”有关的问题是( )。
A.给相框装上花边
B.给一块长方形菜地的四周围上篱笆
C.给学校的窗户安玻璃
D.给一个游泳池注水
5.(2024五下·德江期中)在下图中再添一个小正方形,使它成为一个正方体的展开图,添加的方法共有( )。
A.3种 B.4种 C.5种 D.6种
6.(2024五下·电白期中)一个长方体和一个正方体的体积相等,正方体的棱长是6dm,长方体的高是4dm,长方体的底面积是( )dm2
A.24 B.48 C.54 D.72
7.(2024五下·电白期中)《庄子·天下篇》中有一句话:“一尺之锤,日取其半,万世不竭。”意思是:一根一尺长的木棒,今天取它的一半,明天取它剩下的一半,后天再取剩下的一半,……这样取下去,永远也取不完。那么第三天取的长度就是这根木棍的( )。
A. B. C. D.
8.(2024五下·望都月考) 一根绳子剪成两段,第1段长米,第2段占全长的,两段相比较( )。
A.第1段长 B.第2段长 C.一样长 D.无法确定
9.(2024五下·电白期中)下列各数据中,与其他数据不相等的是( )
A.2700mL B.2.7dm3 C.2.7L D.2.7cm3
10.(2024五下·龙里期中)用棱长为1cm的小正方体拼成棱长为6cm的大正方体后,把大正方体的表面涂上颜色。两面涂色的小正方体有( )个。
A.48 B.8 C.6 D.64
11.(2024五下·洞头期中)把10L的水倒入一个从里面量长2.5dm,宽20cm,高5dm的长方体水缸后,再将一块石头全部浸没入水中,此时水面上升到3.5dm。求这块石头的体积需要用到的信息有( )。
A.10L,2.5dm,20cm,5dm,3.5dm B.2.5dm,20cm,5dm
C.10L,2.5dm,20cm,3.5dm D.2.5dm,20cm,3.5dm
12.(2024五下·龙岗期中)一个长方体的长、宽、高分别扩大到原来的2倍,则这个长方体的表面积扩大到原来的(▲)倍。体积扩大到原来的(▲)倍.此题选( )。
A.2;4 B.4;8 C.6;8 D.8;4
13.(2024五下·电白期中)下面的算式中,( )的积在和之间。
A. B. C. D.
14.(2024五下·电白期中)运用了( )。
A.加法结合律 B.加法交换律
C.分配律 D.加法结合律和加法交换律
15.(2024五下·怀化期中) 如图:把一块长方体木料锯成3个完全相同的正方体,表面积增加了( )cm2。
A.25 B.50 C.100
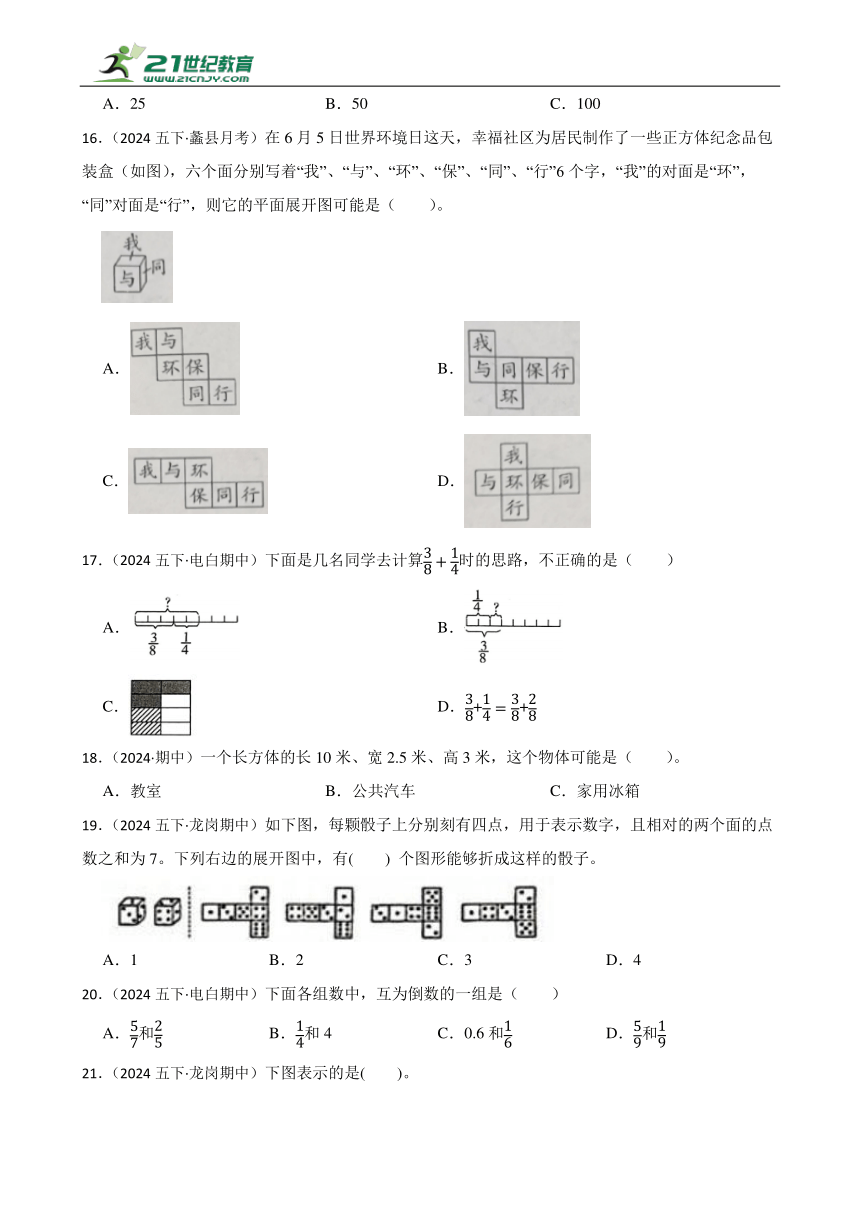
16.(2024五下·蠡县月考)在6月5日世界环境日这天,幸福社区为居民制作了一些正方体纪念品包装盒(如图),六个面分别写着“我”、“与”、“环”、“保”、“同”、“行”6个字,“我”的对面是“环”,“同”对面是“行”,则它的平面展开图可能是( )。
A. B.
C. D.
17.(2024五下·电白期中)下面是几名同学去计算时的思路,不正确的是( )
A. B.
C. D.++
18.(2024·期中)一个长方体的长10米、宽2.5米、高3米,这个物体可能是( )。
A.教室 B.公共汽车 C.家用冰箱
19.(2024五下·龙岗期中)如下图,每颗骰子上分别刻有四点,用于表示数字,且相对的两个面的点数之和为7。下列右边的展开图中,有( ) 个图形能够折成这样的骰子。
A.1 B.2 C.3 D.4
20.(2024五下·电白期中)下面各组数中,互为倒数的一组是( )
A.和 B.和4 C.0.6和 D.和
21.(2024五下·龙岗期中)下图表示的是( )。
A. B. C. D.
22.(2024五下·坪山期中)一个长方体的梭长之和是36厘米,相交于一个顶点的三条棱长之和是( )厘米。
A.9 B.12 C.18 D.15
23.(2024五下·湛江期中)男生人数的与女生人数的相等,男生人数( )女生人数。
A.> B.< C.= D.无法比较
24.(2024五下·电白期中)下面4个正方体展开图,不能折成正方体的是( )。
A. B. C. D.
25.(2024五下·湛江期中) 下面说法错误的是( )。
A.0没有倒数
B.因为0.1X10=1,所以0.1和10互为倒数。
C.假分数的倒数一定小于1
D.1的倒数是1
26.(2024五下·蠡县月考)观察下图,下列说法正确的是( )。
A.甲的表面积大于乙的表面积 B.甲的表面积等于乙的表面积
C.甲的体积小于乙的体积 D.甲的体积等于乙的体积
27.(2024五下·洞头期中)一个长方体高减少2cm后,变成了一个正方体,表面积比原来减少了48cm2,原来长方体的高( ) cm。
A.4 B.6 C.8 D.12
28.(2024五下·威县期中)一根铁丝刚好可以做成一个长16厘米,宽14厘米,高6厘米的长方体,如果用它做成一个正方体,那么正方体的棱长是( )厘米。
A.8 B.10 C.12
29.(2024五下·洞头期中)下列说法正确的是( )。
A.正方体棱长扩大到原来的3倍,体积扩大到原来的9倍。
B.一个自然数如果只有两个因数,那它定是质数。
C.三个连续自然数中一定有一个合数。
D.若是假分数,那么a一定大于5。
30.(2024五下·滕州)从学校去图书馆,悦悦用了小时,乐乐用了0.3小时,( )走得比较快。
A.悦悦 B.乐乐 C.无法确定谁
31.(2024五下·盐都月考)下列哪一种情况用复式折线统计图比较适合( )。
A.1-6 年级男女生人数统计 B.南京和哈尔滨月气温变化情况
C.2010-2016 联想电脑销售情况 D.统计我国陆地各种地形情况
32.(2024五下·龙岗期中)如图所示,几个同样大小的小方块堆积在墙角,已知每个小方块的棱长是1分米,这堆小方块露在外面的面积是( ) 平方分米。
A.10 B.11 C.13 D.15
33.(2024五下·虎门期中)在一个注满水的水缸中,放入两个完全相同的铁块,溢出了60mL的水,那么一个铁块的体积是( )立方厘米。
A.20 B.30 C.60 D.120
34.(2024五下·龙里期中)折叠后,下面的图形不能围成正方体的是( )。
A. B.
C. D.
35.(2024五下·湛江期中)下图中,( )不是正方体的展开图。
A. B.
C. D.
36.(2024五下·洞头期中)下面图形不能围成正方体的是( )。
A. B.
C. D.
37.(2024五下·坪山期中)下图是一个长方体的展开图(单位:dm),则阴影部分的面积是( )dm2。
A.15 B.21 C.35 D.50
38.(2024五下·坪山期中)下图中阴影部分长度是米的是( )
A.
B.
C.
D.
39.(2024五下·虎门期中)一个棱长是1m的正方体,可以切成( )个棱长1dm的正方体。
A.1000 B.100 C.10 D.4
40.(2024五下·坪山期中)下面算式( )的积在和之间。
A. B. C. D.
41.(2024五下·坪山期中)下列算式中,得数最小的是( )
A. B. C. D.
42.(2024五下·虎门期中)把下图的展开图围成正方体后,与E相对的面是( )。
A.A B.B C.C D.D
43.(2024五下·望都月考) 一个无盖的长方体水桶,长a厘米,宽b厘米,高h厘米,做这个水桶用料( )平方厘米。
A.abh B.abh+2ab C.ab+2(bh+ah) D.2(ab+ah+bh)
44.(2024五下·威县期中)把一个长、宽、高分别是8厘米、6厘米、4厘米的长方体截成两个完全相同的长方体,表面积最多增加( )平方厘米。
A.96 B.64 C.48
45.(2024五下·坪山期中)下列各组数中,互为倒数的是( )
A.和 B.和 C.和 D.和
46.(2024五下·洞头期中)用丝带捆扎这个礼盒(如下图),接头处长25 cm,要捆扎这种礼盒需要准备( )长的丝带比铰合理。
A.32cm B.110cm C.132cm D.160cm
47.(2024五下·虎门期中)将一个长方体木块截成两个小长方体木块,说法正确的是( )。
A.表面积增加,体积不变 B.表面积减少,体积不变
C.表面积和体积都增加 D.表面积和体积都不变
48.(2024五下·湛江期中)用一根80 cm长的铁丝焊成一个长方体,长是8cm,宽7cm,高是( )cm。
A.5 B.25 C.50 D.65
49.(2024五下·威县期中)一个长14cm,宽6cm,高0.7cm的长方体形状的物体最有可能是( )。
A.普通手机 B.新华字典 C.抽纸盒
50.(2024五下·威县期中)如下图,甲与乙的表面积相比( )。
A.甲>乙 B.甲<乙 C.甲=乙
答案解析部分
1.C
解:0.5米=5分米,
(4×5×2+2×5×2)×12
=(40+20)×12
=60×12
=720(平方分米)
故答案为:C。
通风管没有底面,因此只需要把两个长4分米、宽0.5米,两个长2分米,宽0.5米的面相加求出一个通风管需要铁皮的面积,然后乘12即可求出至少要用铁皮的面积。
2.C
解:6÷2=3(块),4÷2=2(块),5÷2=2(块)……1(分米),3×2×2=12(块)。
故答案为:C。
用除法分别求出盒子的长、宽、高里面各包含多少个2分米,根据长方体体积的计算方法求出盒子最多能放多少个正方体木块。
3.A
解:假设 正方体的原来的棱长为1,扩大后的棱长则为3;
1×1×1=1×1=1;
3×3×3=9×3=27;
27÷1=27
故答案为:A。
先假设正方体的原来的棱长为1,扩大后的棱长则为3,再根据正方体的体积公式:V=a3,进行计算比较。
4.D
解:A:给相框装上花边是求相框的周长,
B:给一块长方形菜地的四周围上篱笆是求长方形的周长,
C:给学校的窗户安玻璃是求玻璃的面积,
D:给一个游泳池注水是求注水的体积。
故答案为:D。
游泳池一般都是长方形,长方体的长×宽×水的高度=需要注水的体积。
5.B
解:添加的方法共有4种。
故答案为:B。
6.C
解:(6×6×6)÷4
=216÷4
=54( dm2 )
故答案为:C。
根据正方体体积=棱长×棱长×棱长,求出正方体体积,即长方体体积,再根据长方体底面积=体积÷高,列式计算即可。
7.B
解:1×××
=××
= ×
=
故答案为:B。
根据题意,把一根一尺长的木棒看作单位"1”,第一天取它的一半,就是1×;第二天就是取第一天剩下的一半的,即1××;第三天就是取第二天剩下的一半的,即1××× 。
8.B
解:1- =
>,第2段长。
故答案为:B。
第1段占的分率=1-第2段占的分率,然后比较大小。
9.D
解:A:2700mL;
B:2.7dm3×1000=2700cm3=2700mL;
C:2.7L×1000=2700mL;
D:2.7cm3 =2.7mL;
故答案为:D。
把四个选项中的数据化成同单位的数,进行比较即可。
10.A
解:12×(6-2)
=12×4
=48(个)
两面涂色的小正方体有48个。
故答案为:A。
用n表示大正方体每条棱上小正方体的块数,两面涂色的小正方体的块数=12×(n-2)。
11.C
解:需要用到水的体积除以水缸的底面积求出水面的高度,还要用到此时水面上升到的高度,因此用到的信息有10L,2.5dm,20cm,3.5dm。
故答案为:C。
可以用水的体积除以水缸的底面积求出水面的高度,然后用底面积乘水面上升的高度求出石头的体积。还可以用水缸的底面积乘此时水面的高度求出水和石头的体积和,然后减去水的体积就是石头的体积。
12.B
解:2×2=4
2×2×2=8,表面积扩大4倍,体积扩大8倍。
故答案为:B。
长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的长、宽、高分别扩大到原来的2倍,则这个长方体的表面积扩大到原来的4倍。体积扩大到原来的8倍。
13.B
解: =0.2;=0.7
A:==0.1,0.1>0.2,不符合;
B:==,0.2<<0.7,符合;
C:==1.875,1.875>0.7>0.2,不符合;
D:==,>0.7>0.2,不符合;
故答案为:B。
先计算出四个选项中算式的乘积,再分别与和,进行比较即可。
14.D
解:运用了 加法结合律和加法交换律 ;
故答案为:D。
先利用加法交换律把与交换位置,再利用加法结合律把,即。
15.C
解:(3-1)×2
=2×2
=4(个)
5×5×4
=25×4
=100(平方厘米)
所以,如上图,把一块长方体木料锯成3个完全相同的小正方体后,表面积增加了100平方厘米。
故答案为:C
把一块长方体木料锯成3个完全相同的小正方体后,增加了4个面的面积,每个面的面积=棱长x棱长,求出一个面的面积,再乘4即可。
16.B
解:“我”的对面是“环”,“同”对面是“行”,“与”的对面是“保”则它的平面展开图可能是 。
故答案为:B。
正方体相对的面不相邻,则“我”与“环”相对,“同”与“行”相对,“与”与“保”相对。
17.B
解:A项:列式是 ;
B项:列式是-;
C项:列式是;
D项:++ 。
故答案为:B。
A项:总长=两段的长度和;
B项:所求的分率=总量-其中一部分量;
C项:涂色部分占的分率=两种涂色部分的分率和;
D项:异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
18.B
解:A:教室的长不可能是10米;
B:公共汽车的长10米、宽2.5米、高3米,可能;
C:家用冰箱的长大约是1米,宽0.5米。
故答案为:B。
根据实际情况判断长10米、宽2.5米、高3米的长方体是哪种物体即可。
19.B
解:这两个相对的面相加分别是3+4=1+6=5+2,共2个。
故答案为:B。
正方体相对的面不相邻,据此进行判断后再把相对两个面的点数相加进行验证。
20.B
解:A:的倒数是,选项错误;
B:的倒数是4,选项正确;
C:的倒数是6,选项错误;
D:的倒数是,选项错误;
故答案为:B。
分别求出四个选择中倒数,再与原选项对比即可。
21.D
解:-= 。
故答案为:D。
把单位“1”平均分成6份,每份是,取其中的几份就是六分之几,这个图表示的是-= 。
22.A
解:36÷4=9(厘米)
故答案为:A。
长方体棱长和=(长+宽+高)×4,因此用棱长和除以4即可求出一组长宽高的和,也就是相交与一个顶点的三条棱长之和。
23.B
解:男生人数×=女生人数×,>,所以男生人数<女生人数。
故答案为:B。
根据分数的意义得到男生人数×=女生人数×,乘积相等,所以一个因数大,另一个因数就小,所以只需要比较两个分数的大小即可确定男生和女生人数的多少。
24.C
解:A:属于”1-4-1“结构,能折成正方体 ;
B:属于”2-2-2“结构,能 折成正方体 ;
C:不属于正方体展开图有11种特征的其中一种,不能折成正方体;
D:属于”2-3-1“结构,能 折成正方体 ;
故答案为:C。
正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1“"结构,即第一行放1个,第二行放4个,第三行放1个;
第二种:"2-2-2"结构,即每一行放2个正方形,此种结向只有一种展开图;
第三种:“3-3"结构,即每一行放3个正方形,只有一种展开图;
第四种:“1-3-2"结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形;据此选择。
25.C
解:假分数的倒数小于或等于1,原来说法错误。
故答案为:C。
A:乘积是1的两个数互为倒数,0没有倒数;
B:根据倒数的意义判断,因为0.1X10=1,所以0.1和10互为倒数;
C:假分数大于或等于1,所以假分数的倒数小于或等于1;
D:1×1=1,所以1的倒数是1。
26.B
解:甲比乙多了一个小正方体,多了3个小正方体面的面积,乙又多露出3个小正方体面的面积,则甲、乙的表面积相等;
甲的体积比乙的体积多了1个小正方体的体积。
故答案为:B。
甲的表面积=乙的表面积,甲的体积>乙的体积。
27.C
解:底面边长:48÷4÷2=6(cm),原来长方体的高6+2=8(cm)。
故答案为:C。
因为高减少2cm,就变成了正方体,说明长方体的底面是正方形,那么减少部分的四个侧面是完全相同的长方形。用减少部分的表面积除以4求出一个侧面的面积,用一个侧面的面积除以2即可求出底面边长。用底面边长加上高减少的部分即可求出原来长方体的高。
28.C
解:(16+14+6)×4÷12
=36×4÷12
=144÷12
=12(厘米)。
故答案为:C。
正方体的棱长=正方体的棱长和÷12;其中,正方体的棱长和=长方体的棱长和=(长+宽+高)×4。
29.B
解:A:正方体棱长扩大到原来的3倍,体积扩大到原来的27倍。原来说法错误;
B:一个自然数如果只有两个因数,那它定是质数。原来说法正确;
C:三个连续自然数中不一定有一个合数。原来说法错误;
D:若是假分数,那么a一定大于等于5。原来说法错误。
故答案为:B。
A:正方体体积=棱长×棱长×棱长,正方体体积扩大的倍数是棱长扩大倍数的立方倍;
B:只有1和本身两个因数的数是质数;
C:例如连续的自然数1、2、3,就没有合数;
D:假分数的分子大于等于分母。
30.A
解:因为=0.2,0.2<0.3,所以悦悦走得比较快。
故答案为:A。
从学校到图书馆的路程是不变的,谁用的时间越短,速度越快。
31.B
解:南京和哈尔滨月气温变化情况,统计的两个地方的气温变化情况,选择复式折线统计图比较适合。
故答案为:B。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
32.D
解:(1×1)×(6+5+4)
=1×15
=15(平方分米)
故答案为:D。
这堆小方块露在外面的面积=小正方体的棱长×棱长×(从前面看露在外面的面个数+从右面看露在外面的面个数+从上面看露在外面的面个数)。
33.B
解:60÷2=30(毫升)
30毫升=30立方厘米
故答案为:B。
把两个完全相同的铁块放入装满水的水缸里,溢出的水的体积就是两块铁块的体积,用两块铁块的体积除以2,就是一个铁块的体积。
34.A
解:第一个图形不符合围成正方体的任何一种形式,
所以第一个图形不能围成正方体。
故答案为:A。
35.C
解:、、折叠后没有重叠的面,是正方体展开图;折叠后有重叠的面,不是正方体的展开图。
故答案为:C。
沿着虚线折叠后没有重叠的面就是正方体展开图,折叠后有重叠的面,就不是正方体的展开图。
36.C
解:、、都能围成正方体,不能围成正方体。
故答案为:C。
折叠后有重叠的面就不能围成正方体,没有重叠的面就能围成正方体。
37.B
解:7×3=21(dm2)
故答案为:B。
阴影部分是一个长方形,长是7dm,宽是3dm,根据长方形面积公式计算阴影部分的面积。
38.B
解:A:3×=(米);
B:3×=(米);
C:4×=3(米);
D:4×=1(米)。
故答案为:B。
根据分数的意义判断出每个图中阴影部分是整个图形的几分之几,然后根据分数乘法的意义求出阴影部分的长度即可。
39.A
解:10×10×10=1000(个)
一个棱长为1m的正方体,可以切割成1000个棱长为1dm的正方体。
故答案为:A。
把棱长为1m的正方体,切割成棱长为1dm的正方体,1m=10dm,这个长方体的长、宽、高均被切割成10份,这样就切割成了(10×10×10)个棱长为1dm的正方体。
40.B
解:A:<1,所以<;
B:=,在和之间;
C:<1,所以<;
D:>1,所以>。
故答案为:B。
A:一个非0数乘小于1的数,积小于这个数;
B:根据分数乘分数的计算方法计算出积,然后判断积的大小;
C:一个非0数乘小于1的数,积小于这个数;
D:一个非0数乘大于1的数,积大于这个数。
41.C
解:A:=;
B:=;
C:=;
D:=;
得数最小的是。
故答案为:C。
分数与整数相加,用带分数表示和;分数与分数相乘,用分子相乘的积做分子,分母相乘的积做分母,能约分的要先约分再乘。
42.D
解:与E相对的面是D,与C相对的面是B,与A相对的面是F。
故答案为:D。
正方体相对的面不相邻,则E和D相对,C和B相对,A和F相对。
43.C
解:ab+(ah+bh)×2=ab+2(bh+ah) 。
故答案为:C。
做这个水桶用料的面积=长×宽+(长×高+宽×高)×2。
44.A
解:8×6×2
=48×2
=96(平方厘米)。
故答案为:A。
最多增加的表面积=最大一个面的长×宽×2。
45.D
解:A:×=,不是互为倒数;
B:×3=,不是互为倒数;
C:×0.3=0.1,不是互为倒数;
D:0.25×4=1,互为倒数。
故答案为:D。
乘积是1的两个数互为倒数,根据倒数的意义判断即可。
46.B
解:10×2+15×2+8×4+25
=20+30+32+25
=107(cm)
110cm比107cm多一些,比较合理。
故答案为:B。
长10cm的2条,宽15cm的2条,高8cm的4条,把这些长度相加,再加上接头处的长度,求出至少需要丝带的长度。准备时只需要比至少需要的长度多一些即可。132cm和160cm比107多得多,所以不合理。
47.A
解:将一个长方体木块截成两个小长方体木块,表面积增加了两个相互粘合的面,体积是两个小长方体的体积之和,体积不变。
故答案为:A。
将一个长方体木块截成两个小长方体木块,表面积增加了两个相互粘合的面,体积是两个小长方体的体积之和,体积不变。
48.A
解:80÷4-8-7
=20-8-7
=5(cm)
故答案为:A。
长方体棱长和=(长+宽+高)×4,因此用铁丝的长度除以4求出一组长宽高的和,然后用一组长宽高的和减去长和宽即可求出高。
49.A
解:普通手机的长、宽、高可能是14厘米、6厘米、0.7厘米。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行选择。
50.C
解:甲的表面积是原来正方体的表面积减去减少面的面积,再加上露出面的面积,与原来正方体的表面积相等,则甲的表面积=乙的表面积。
故答案为:C。
甲减去减少面的面积,再加上露出面的面积,还等于原来的表面积。
期中考试真题分类汇编03 单项选择
一、单选题
1.(2024五下·高要期中)要制作12节长方体的铁皮通风管,每节长4分米,宽2分米,高0.5米(如右图所示),至少要用( )平方分米的铁皮。
A.48 B.672 C.720 D.912
2.(2024五下·潮南期中)一个长6dm,宽4dm,高5dm的长方体盒子,最多能放( )个2厘米的小正方体。
A.5 B.14 C.12
3.(2024五下·电白期中)正方体的棱长扩大到原来的3倍,体积扩大( )倍。
A.27 B.9 C.6 D.3
4.(2024五下·德江期中)下面现实情境中最适合提出与“体积”有关的问题是( )。
A.给相框装上花边
B.给一块长方形菜地的四周围上篱笆
C.给学校的窗户安玻璃
D.给一个游泳池注水
5.(2024五下·德江期中)在下图中再添一个小正方形,使它成为一个正方体的展开图,添加的方法共有( )。
A.3种 B.4种 C.5种 D.6种
6.(2024五下·电白期中)一个长方体和一个正方体的体积相等,正方体的棱长是6dm,长方体的高是4dm,长方体的底面积是( )dm2
A.24 B.48 C.54 D.72
7.(2024五下·电白期中)《庄子·天下篇》中有一句话:“一尺之锤,日取其半,万世不竭。”意思是:一根一尺长的木棒,今天取它的一半,明天取它剩下的一半,后天再取剩下的一半,……这样取下去,永远也取不完。那么第三天取的长度就是这根木棍的( )。
A. B. C. D.
8.(2024五下·望都月考) 一根绳子剪成两段,第1段长米,第2段占全长的,两段相比较( )。
A.第1段长 B.第2段长 C.一样长 D.无法确定
9.(2024五下·电白期中)下列各数据中,与其他数据不相等的是( )
A.2700mL B.2.7dm3 C.2.7L D.2.7cm3
10.(2024五下·龙里期中)用棱长为1cm的小正方体拼成棱长为6cm的大正方体后,把大正方体的表面涂上颜色。两面涂色的小正方体有( )个。
A.48 B.8 C.6 D.64
11.(2024五下·洞头期中)把10L的水倒入一个从里面量长2.5dm,宽20cm,高5dm的长方体水缸后,再将一块石头全部浸没入水中,此时水面上升到3.5dm。求这块石头的体积需要用到的信息有( )。
A.10L,2.5dm,20cm,5dm,3.5dm B.2.5dm,20cm,5dm
C.10L,2.5dm,20cm,3.5dm D.2.5dm,20cm,3.5dm
12.(2024五下·龙岗期中)一个长方体的长、宽、高分别扩大到原来的2倍,则这个长方体的表面积扩大到原来的(▲)倍。体积扩大到原来的(▲)倍.此题选( )。
A.2;4 B.4;8 C.6;8 D.8;4
13.(2024五下·电白期中)下面的算式中,( )的积在和之间。
A. B. C. D.
14.(2024五下·电白期中)运用了( )。
A.加法结合律 B.加法交换律
C.分配律 D.加法结合律和加法交换律
15.(2024五下·怀化期中) 如图:把一块长方体木料锯成3个完全相同的正方体,表面积增加了( )cm2。
A.25 B.50 C.100
16.(2024五下·蠡县月考)在6月5日世界环境日这天,幸福社区为居民制作了一些正方体纪念品包装盒(如图),六个面分别写着“我”、“与”、“环”、“保”、“同”、“行”6个字,“我”的对面是“环”,“同”对面是“行”,则它的平面展开图可能是( )。
A. B.
C. D.
17.(2024五下·电白期中)下面是几名同学去计算时的思路,不正确的是( )
A. B.
C. D.++
18.(2024·期中)一个长方体的长10米、宽2.5米、高3米,这个物体可能是( )。
A.教室 B.公共汽车 C.家用冰箱
19.(2024五下·龙岗期中)如下图,每颗骰子上分别刻有四点,用于表示数字,且相对的两个面的点数之和为7。下列右边的展开图中,有( ) 个图形能够折成这样的骰子。
A.1 B.2 C.3 D.4
20.(2024五下·电白期中)下面各组数中,互为倒数的一组是( )
A.和 B.和4 C.0.6和 D.和
21.(2024五下·龙岗期中)下图表示的是( )。
A. B. C. D.
22.(2024五下·坪山期中)一个长方体的梭长之和是36厘米,相交于一个顶点的三条棱长之和是( )厘米。
A.9 B.12 C.18 D.15
23.(2024五下·湛江期中)男生人数的与女生人数的相等,男生人数( )女生人数。
A.> B.< C.= D.无法比较
24.(2024五下·电白期中)下面4个正方体展开图,不能折成正方体的是( )。
A. B. C. D.
25.(2024五下·湛江期中) 下面说法错误的是( )。
A.0没有倒数
B.因为0.1X10=1,所以0.1和10互为倒数。
C.假分数的倒数一定小于1
D.1的倒数是1
26.(2024五下·蠡县月考)观察下图,下列说法正确的是( )。
A.甲的表面积大于乙的表面积 B.甲的表面积等于乙的表面积
C.甲的体积小于乙的体积 D.甲的体积等于乙的体积
27.(2024五下·洞头期中)一个长方体高减少2cm后,变成了一个正方体,表面积比原来减少了48cm2,原来长方体的高( ) cm。
A.4 B.6 C.8 D.12
28.(2024五下·威县期中)一根铁丝刚好可以做成一个长16厘米,宽14厘米,高6厘米的长方体,如果用它做成一个正方体,那么正方体的棱长是( )厘米。
A.8 B.10 C.12
29.(2024五下·洞头期中)下列说法正确的是( )。
A.正方体棱长扩大到原来的3倍,体积扩大到原来的9倍。
B.一个自然数如果只有两个因数,那它定是质数。
C.三个连续自然数中一定有一个合数。
D.若是假分数,那么a一定大于5。
30.(2024五下·滕州)从学校去图书馆,悦悦用了小时,乐乐用了0.3小时,( )走得比较快。
A.悦悦 B.乐乐 C.无法确定谁
31.(2024五下·盐都月考)下列哪一种情况用复式折线统计图比较适合( )。
A.1-6 年级男女生人数统计 B.南京和哈尔滨月气温变化情况
C.2010-2016 联想电脑销售情况 D.统计我国陆地各种地形情况
32.(2024五下·龙岗期中)如图所示,几个同样大小的小方块堆积在墙角,已知每个小方块的棱长是1分米,这堆小方块露在外面的面积是( ) 平方分米。
A.10 B.11 C.13 D.15
33.(2024五下·虎门期中)在一个注满水的水缸中,放入两个完全相同的铁块,溢出了60mL的水,那么一个铁块的体积是( )立方厘米。
A.20 B.30 C.60 D.120
34.(2024五下·龙里期中)折叠后,下面的图形不能围成正方体的是( )。
A. B.
C. D.
35.(2024五下·湛江期中)下图中,( )不是正方体的展开图。
A. B.
C. D.
36.(2024五下·洞头期中)下面图形不能围成正方体的是( )。
A. B.
C. D.
37.(2024五下·坪山期中)下图是一个长方体的展开图(单位:dm),则阴影部分的面积是( )dm2。
A.15 B.21 C.35 D.50
38.(2024五下·坪山期中)下图中阴影部分长度是米的是( )
A.
B.
C.
D.
39.(2024五下·虎门期中)一个棱长是1m的正方体,可以切成( )个棱长1dm的正方体。
A.1000 B.100 C.10 D.4
40.(2024五下·坪山期中)下面算式( )的积在和之间。
A. B. C. D.
41.(2024五下·坪山期中)下列算式中,得数最小的是( )
A. B. C. D.
42.(2024五下·虎门期中)把下图的展开图围成正方体后,与E相对的面是( )。
A.A B.B C.C D.D
43.(2024五下·望都月考) 一个无盖的长方体水桶,长a厘米,宽b厘米,高h厘米,做这个水桶用料( )平方厘米。
A.abh B.abh+2ab C.ab+2(bh+ah) D.2(ab+ah+bh)
44.(2024五下·威县期中)把一个长、宽、高分别是8厘米、6厘米、4厘米的长方体截成两个完全相同的长方体,表面积最多增加( )平方厘米。
A.96 B.64 C.48
45.(2024五下·坪山期中)下列各组数中,互为倒数的是( )
A.和 B.和 C.和 D.和
46.(2024五下·洞头期中)用丝带捆扎这个礼盒(如下图),接头处长25 cm,要捆扎这种礼盒需要准备( )长的丝带比铰合理。
A.32cm B.110cm C.132cm D.160cm
47.(2024五下·虎门期中)将一个长方体木块截成两个小长方体木块,说法正确的是( )。
A.表面积增加,体积不变 B.表面积减少,体积不变
C.表面积和体积都增加 D.表面积和体积都不变
48.(2024五下·湛江期中)用一根80 cm长的铁丝焊成一个长方体,长是8cm,宽7cm,高是( )cm。
A.5 B.25 C.50 D.65
49.(2024五下·威县期中)一个长14cm,宽6cm,高0.7cm的长方体形状的物体最有可能是( )。
A.普通手机 B.新华字典 C.抽纸盒
50.(2024五下·威县期中)如下图,甲与乙的表面积相比( )。
A.甲>乙 B.甲<乙 C.甲=乙
答案解析部分
1.C
解:0.5米=5分米,
(4×5×2+2×5×2)×12
=(40+20)×12
=60×12
=720(平方分米)
故答案为:C。
通风管没有底面,因此只需要把两个长4分米、宽0.5米,两个长2分米,宽0.5米的面相加求出一个通风管需要铁皮的面积,然后乘12即可求出至少要用铁皮的面积。
2.C
解:6÷2=3(块),4÷2=2(块),5÷2=2(块)……1(分米),3×2×2=12(块)。
故答案为:C。
用除法分别求出盒子的长、宽、高里面各包含多少个2分米,根据长方体体积的计算方法求出盒子最多能放多少个正方体木块。
3.A
解:假设 正方体的原来的棱长为1,扩大后的棱长则为3;
1×1×1=1×1=1;
3×3×3=9×3=27;
27÷1=27
故答案为:A。
先假设正方体的原来的棱长为1,扩大后的棱长则为3,再根据正方体的体积公式:V=a3,进行计算比较。
4.D
解:A:给相框装上花边是求相框的周长,
B:给一块长方形菜地的四周围上篱笆是求长方形的周长,
C:给学校的窗户安玻璃是求玻璃的面积,
D:给一个游泳池注水是求注水的体积。
故答案为:D。
游泳池一般都是长方形,长方体的长×宽×水的高度=需要注水的体积。
5.B
解:添加的方法共有4种。
故答案为:B。
6.C
解:(6×6×6)÷4
=216÷4
=54( dm2 )
故答案为:C。
根据正方体体积=棱长×棱长×棱长,求出正方体体积,即长方体体积,再根据长方体底面积=体积÷高,列式计算即可。
7.B
解:1×××
=××
= ×
=
故答案为:B。
根据题意,把一根一尺长的木棒看作单位"1”,第一天取它的一半,就是1×;第二天就是取第一天剩下的一半的,即1××;第三天就是取第二天剩下的一半的,即1××× 。
8.B
解:1- =
>,第2段长。
故答案为:B。
第1段占的分率=1-第2段占的分率,然后比较大小。
9.D
解:A:2700mL;
B:2.7dm3×1000=2700cm3=2700mL;
C:2.7L×1000=2700mL;
D:2.7cm3 =2.7mL;
故答案为:D。
把四个选项中的数据化成同单位的数,进行比较即可。
10.A
解:12×(6-2)
=12×4
=48(个)
两面涂色的小正方体有48个。
故答案为:A。
用n表示大正方体每条棱上小正方体的块数,两面涂色的小正方体的块数=12×(n-2)。
11.C
解:需要用到水的体积除以水缸的底面积求出水面的高度,还要用到此时水面上升到的高度,因此用到的信息有10L,2.5dm,20cm,3.5dm。
故答案为:C。
可以用水的体积除以水缸的底面积求出水面的高度,然后用底面积乘水面上升的高度求出石头的体积。还可以用水缸的底面积乘此时水面的高度求出水和石头的体积和,然后减去水的体积就是石头的体积。
12.B
解:2×2=4
2×2×2=8,表面积扩大4倍,体积扩大8倍。
故答案为:B。
长方体的体积=长×宽×高;长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的长、宽、高分别扩大到原来的2倍,则这个长方体的表面积扩大到原来的4倍。体积扩大到原来的8倍。
13.B
解: =0.2;=0.7
A:==0.1,0.1>0.2,不符合;
B:==,0.2<<0.7,符合;
C:==1.875,1.875>0.7>0.2,不符合;
D:==,>0.7>0.2,不符合;
故答案为:B。
先计算出四个选项中算式的乘积,再分别与和,进行比较即可。
14.D
解:运用了 加法结合律和加法交换律 ;
故答案为:D。
先利用加法交换律把与交换位置,再利用加法结合律把,即。
15.C
解:(3-1)×2
=2×2
=4(个)
5×5×4
=25×4
=100(平方厘米)
所以,如上图,把一块长方体木料锯成3个完全相同的小正方体后,表面积增加了100平方厘米。
故答案为:C
把一块长方体木料锯成3个完全相同的小正方体后,增加了4个面的面积,每个面的面积=棱长x棱长,求出一个面的面积,再乘4即可。
16.B
解:“我”的对面是“环”,“同”对面是“行”,“与”的对面是“保”则它的平面展开图可能是 。
故答案为:B。
正方体相对的面不相邻,则“我”与“环”相对,“同”与“行”相对,“与”与“保”相对。
17.B
解:A项:列式是 ;
B项:列式是-;
C项:列式是;
D项:++ 。
故答案为:B。
A项:总长=两段的长度和;
B项:所求的分率=总量-其中一部分量;
C项:涂色部分占的分率=两种涂色部分的分率和;
D项:异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
18.B
解:A:教室的长不可能是10米;
B:公共汽车的长10米、宽2.5米、高3米,可能;
C:家用冰箱的长大约是1米,宽0.5米。
故答案为:B。
根据实际情况判断长10米、宽2.5米、高3米的长方体是哪种物体即可。
19.B
解:这两个相对的面相加分别是3+4=1+6=5+2,共2个。
故答案为:B。
正方体相对的面不相邻,据此进行判断后再把相对两个面的点数相加进行验证。
20.B
解:A:的倒数是,选项错误;
B:的倒数是4,选项正确;
C:的倒数是6,选项错误;
D:的倒数是,选项错误;
故答案为:B。
分别求出四个选择中倒数,再与原选项对比即可。
21.D
解:-= 。
故答案为:D。
把单位“1”平均分成6份,每份是,取其中的几份就是六分之几,这个图表示的是-= 。
22.A
解:36÷4=9(厘米)
故答案为:A。
长方体棱长和=(长+宽+高)×4,因此用棱长和除以4即可求出一组长宽高的和,也就是相交与一个顶点的三条棱长之和。
23.B
解:男生人数×=女生人数×,>,所以男生人数<女生人数。
故答案为:B。
根据分数的意义得到男生人数×=女生人数×,乘积相等,所以一个因数大,另一个因数就小,所以只需要比较两个分数的大小即可确定男生和女生人数的多少。
24.C
解:A:属于”1-4-1“结构,能折成正方体 ;
B:属于”2-2-2“结构,能 折成正方体 ;
C:不属于正方体展开图有11种特征的其中一种,不能折成正方体;
D:属于”2-3-1“结构,能 折成正方体 ;
故答案为:C。
正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1“"结构,即第一行放1个,第二行放4个,第三行放1个;
第二种:"2-2-2"结构,即每一行放2个正方形,此种结向只有一种展开图;
第三种:“3-3"结构,即每一行放3个正方形,只有一种展开图;
第四种:“1-3-2"结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形;据此选择。
25.C
解:假分数的倒数小于或等于1,原来说法错误。
故答案为:C。
A:乘积是1的两个数互为倒数,0没有倒数;
B:根据倒数的意义判断,因为0.1X10=1,所以0.1和10互为倒数;
C:假分数大于或等于1,所以假分数的倒数小于或等于1;
D:1×1=1,所以1的倒数是1。
26.B
解:甲比乙多了一个小正方体,多了3个小正方体面的面积,乙又多露出3个小正方体面的面积,则甲、乙的表面积相等;
甲的体积比乙的体积多了1个小正方体的体积。
故答案为:B。
甲的表面积=乙的表面积,甲的体积>乙的体积。
27.C
解:底面边长:48÷4÷2=6(cm),原来长方体的高6+2=8(cm)。
故答案为:C。
因为高减少2cm,就变成了正方体,说明长方体的底面是正方形,那么减少部分的四个侧面是完全相同的长方形。用减少部分的表面积除以4求出一个侧面的面积,用一个侧面的面积除以2即可求出底面边长。用底面边长加上高减少的部分即可求出原来长方体的高。
28.C
解:(16+14+6)×4÷12
=36×4÷12
=144÷12
=12(厘米)。
故答案为:C。
正方体的棱长=正方体的棱长和÷12;其中,正方体的棱长和=长方体的棱长和=(长+宽+高)×4。
29.B
解:A:正方体棱长扩大到原来的3倍,体积扩大到原来的27倍。原来说法错误;
B:一个自然数如果只有两个因数,那它定是质数。原来说法正确;
C:三个连续自然数中不一定有一个合数。原来说法错误;
D:若是假分数,那么a一定大于等于5。原来说法错误。
故答案为:B。
A:正方体体积=棱长×棱长×棱长,正方体体积扩大的倍数是棱长扩大倍数的立方倍;
B:只有1和本身两个因数的数是质数;
C:例如连续的自然数1、2、3,就没有合数;
D:假分数的分子大于等于分母。
30.A
解:因为=0.2,0.2<0.3,所以悦悦走得比较快。
故答案为:A。
从学校到图书馆的路程是不变的,谁用的时间越短,速度越快。
31.B
解:南京和哈尔滨月气温变化情况,统计的两个地方的气温变化情况,选择复式折线统计图比较适合。
故答案为:B。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
32.D
解:(1×1)×(6+5+4)
=1×15
=15(平方分米)
故答案为:D。
这堆小方块露在外面的面积=小正方体的棱长×棱长×(从前面看露在外面的面个数+从右面看露在外面的面个数+从上面看露在外面的面个数)。
33.B
解:60÷2=30(毫升)
30毫升=30立方厘米
故答案为:B。
把两个完全相同的铁块放入装满水的水缸里,溢出的水的体积就是两块铁块的体积,用两块铁块的体积除以2,就是一个铁块的体积。
34.A
解:第一个图形不符合围成正方体的任何一种形式,
所以第一个图形不能围成正方体。
故答案为:A。
35.C
解:、、折叠后没有重叠的面,是正方体展开图;折叠后有重叠的面,不是正方体的展开图。
故答案为:C。
沿着虚线折叠后没有重叠的面就是正方体展开图,折叠后有重叠的面,就不是正方体的展开图。
36.C
解:、、都能围成正方体,不能围成正方体。
故答案为:C。
折叠后有重叠的面就不能围成正方体,没有重叠的面就能围成正方体。
37.B
解:7×3=21(dm2)
故答案为:B。
阴影部分是一个长方形,长是7dm,宽是3dm,根据长方形面积公式计算阴影部分的面积。
38.B
解:A:3×=(米);
B:3×=(米);
C:4×=3(米);
D:4×=1(米)。
故答案为:B。
根据分数的意义判断出每个图中阴影部分是整个图形的几分之几,然后根据分数乘法的意义求出阴影部分的长度即可。
39.A
解:10×10×10=1000(个)
一个棱长为1m的正方体,可以切割成1000个棱长为1dm的正方体。
故答案为:A。
把棱长为1m的正方体,切割成棱长为1dm的正方体,1m=10dm,这个长方体的长、宽、高均被切割成10份,这样就切割成了(10×10×10)个棱长为1dm的正方体。
40.B
解:A:<1,所以<;
B:=,在和之间;
C:<1,所以<;
D:>1,所以>。
故答案为:B。
A:一个非0数乘小于1的数,积小于这个数;
B:根据分数乘分数的计算方法计算出积,然后判断积的大小;
C:一个非0数乘小于1的数,积小于这个数;
D:一个非0数乘大于1的数,积大于这个数。
41.C
解:A:=;
B:=;
C:=;
D:=;
得数最小的是。
故答案为:C。
分数与整数相加,用带分数表示和;分数与分数相乘,用分子相乘的积做分子,分母相乘的积做分母,能约分的要先约分再乘。
42.D
解:与E相对的面是D,与C相对的面是B,与A相对的面是F。
故答案为:D。
正方体相对的面不相邻,则E和D相对,C和B相对,A和F相对。
43.C
解:ab+(ah+bh)×2=ab+2(bh+ah) 。
故答案为:C。
做这个水桶用料的面积=长×宽+(长×高+宽×高)×2。
44.A
解:8×6×2
=48×2
=96(平方厘米)。
故答案为:A。
最多增加的表面积=最大一个面的长×宽×2。
45.D
解:A:×=,不是互为倒数;
B:×3=,不是互为倒数;
C:×0.3=0.1,不是互为倒数;
D:0.25×4=1,互为倒数。
故答案为:D。
乘积是1的两个数互为倒数,根据倒数的意义判断即可。
46.B
解:10×2+15×2+8×4+25
=20+30+32+25
=107(cm)
110cm比107cm多一些,比较合理。
故答案为:B。
长10cm的2条,宽15cm的2条,高8cm的4条,把这些长度相加,再加上接头处的长度,求出至少需要丝带的长度。准备时只需要比至少需要的长度多一些即可。132cm和160cm比107多得多,所以不合理。
47.A
解:将一个长方体木块截成两个小长方体木块,表面积增加了两个相互粘合的面,体积是两个小长方体的体积之和,体积不变。
故答案为:A。
将一个长方体木块截成两个小长方体木块,表面积增加了两个相互粘合的面,体积是两个小长方体的体积之和,体积不变。
48.A
解:80÷4-8-7
=20-8-7
=5(cm)
故答案为:A。
长方体棱长和=(长+宽+高)×4,因此用铁丝的长度除以4求出一组长宽高的和,然后用一组长宽高的和减去长和宽即可求出高。
49.A
解:普通手机的长、宽、高可能是14厘米、6厘米、0.7厘米。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行选择。
50.C
解:甲的表面积是原来正方体的表面积减去减少面的面积,再加上露出面的面积,与原来正方体的表面积相等,则甲的表面积=乙的表面积。
故答案为:C。
甲减去减少面的面积,再加上露出面的面积,还等于原来的表面积。
同课章节目录
