期中考试真题分类汇编01单项选择(含答案+解析)---2024-2025学年北师大版六年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编01单项选择(含答案+解析)---2024-2025学年北师大版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 08:15:42 | ||
图片预览




文档简介
2024-2025学年北师大版六年级数学下册
期中考试真题分类汇编01单项选择
一、单选题
1.(2024六下·蓬江期中)“宫、商、角、徵、羽”是我国古代音乐的基本音阶。基本音阶“商”的发音管比基本音阶“徵”的发音管短,则“徵”和“商”的发音管长度比是( )。
A.3:2 B.2:3 C.4:3 D.3:4
2.(2024六下·江门期中)购买儿童阅读这本书,总价与( )成正比例。
A.书的本数 B.书的页数 C.书的单价
3.(2024六下·江门期中)一个圆锥体积是 12.56cm3,比等底等商的圆柱体积少了( ) cm3
A.6.28 B.12.56 C.25.12
4.(2024六下·江门期中)一个圆柱的底面半径和高都扩大3倍,它的体积扩大( )倍。
A.9 B.27 C.6
5.(2024六下·江门期中)一个圆柱体的底面半径是3厘米,高是18.84厘米,它的侧面展开图是( )。
A.正方形
B.长方形
C.两个圆形和一个长方形组成
6.(2024六下·江门期中)在比例中,两个外项互为倒数,两个内项( )
A.成正比例 B.成反比例 C.不成比例
7.(2024六下·玉田期中)如下图所示,如果以一条直角边为轴旋转一周,得到的图形的体积是( )cm3。
A.37.68 B.50.24 C.37.68或50.24
8.(2024六下·玉田期中)下面说法错误的是( )
A.0是最小的整数。
B.圆锥的侧面展开后是一个扇形。
C.一个保温杯最多装水450毫升,说明它的容积是450毫升。
9.(2024六下·玉田期中)铺地的面积一定,用砖的总块数和每块砖的( )成反比例。
A.边长 B.周长 C.面积
10.(2024六下·玉田期中) 一个圆锥形零件,体积是16立方厘米,底面积是20平方厘米,它的高是( )厘米。
A.2.4 B.0.8 C.12.5
11.(2024六下·玉田期中)某工厂生产了一种饮料桶,尺寸如图所示。(单位:厘米)下面有三种饮料筒侧面的商标纸,你认为哪种纸比较合适?( )
A.
B.
C.
12.(2024六下·玉田期中)红红在数室里的位置用数对表示是(3,5),下面的数对中,( )表示的位置一定不是她的同桌。
A.(2,5) B.(3,4) C.(4,5)
13.(2024六下·玉田期中)关于正比例和反比例,说法错误的是( )
A.圆的周长和它的直径成正比例。
B.彩带的总长度一定,用去的米数和剩下的米数成反比例。
C.比值一定,比的前项和后项成正比例。
14.(2024六下·玉田期中)一袋食用盐上写着“净重500±5g”,说明每袋盐的实际质量不低于( )g。
A.495 B.500 C.505
15.(2024六下·柳州期中)小军将一根长10厘米的铁丝分成三段,再首尾相连组成一个三角形。下面图( )的方法一定能围成一个三角形。
A.
B.
C.
D.
16.(2024六下·柳州期中)下面是2024年柳州马拉松的信息,其中成正比例关系的是( )
A.参加马拉松的男运动员人数与女运动员人数。
B.小思参加了“欢乐跑”,她跑步的速度与时间。
C.用相同的大巴车接送参加马拉松的学生,在每辆车坐满的情况下,接送学生的总人数与大巴车的数量。
D.开跑1小时后,李叔叔已经跑的路程与未跑的路程。
17.(2024六下·柳州期中)数轴上有2个数,分别是E、F(如图)。下列式子结果最大的是( )
A.F+E B.F﹣E C.F×E D.F÷E
18.(2024六下·柳州期中)有3个连续奇数,其中最小的奇数是n,则这3个奇数的和是( )
A.3(n+1) B.3(n+2) C.3(n+6) D.3n
19.(2024六下·柳州期中)诗句“黄河远上白云间,一片孤城万仞山”中的“仞”在古代是一个长度单位,以周、秦、汉的度量衡来论,“一仞”就是八尺,一尺等于23.1厘米。那么“一仞”相当于( )
A.成年人的身高 B.成年人一臂的长度
C.成年人一掌的长度 D.成年人一拃的长度
20.(2024六下·柳州期中)为了研究“14亿粒米有多重”这个问题。六⑴班同学在数学活动课中进行了操作,其中第一小组数出200粒米,称得质量为4克,以此计算后得到14亿粒大米大约重( )吨。
A.28 B.56 C.5600 D.2.8
21.(2024六下·黄石期中) 一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是( )
A.1:2π B.1:π C.π:1 D.1:1
22.(2024六下·黄石期中)我国2023年的出生人口为902万人,出生率为6.39%。这个6.39%叫( )数。
A.百分数 B.千分数 C.万分数 D.都可以
23.(2024六下·黄石期中) 一种商品,先提价10%后,再打九折出售( )
A.比原价高 B.比原价低 C.与原价相同 D.无法确定
24.(2024六下·黄石期中)看一本书,已经看的页数a与未看的页数b是( )关系。
A.没有 B.正比例 C.反比例 D.和一定
25.(2024六下·黄石期中)如果x=5y,x和y成( )比例关系。
A.正比例 B.反比例 C.不成比例 D.无法确定
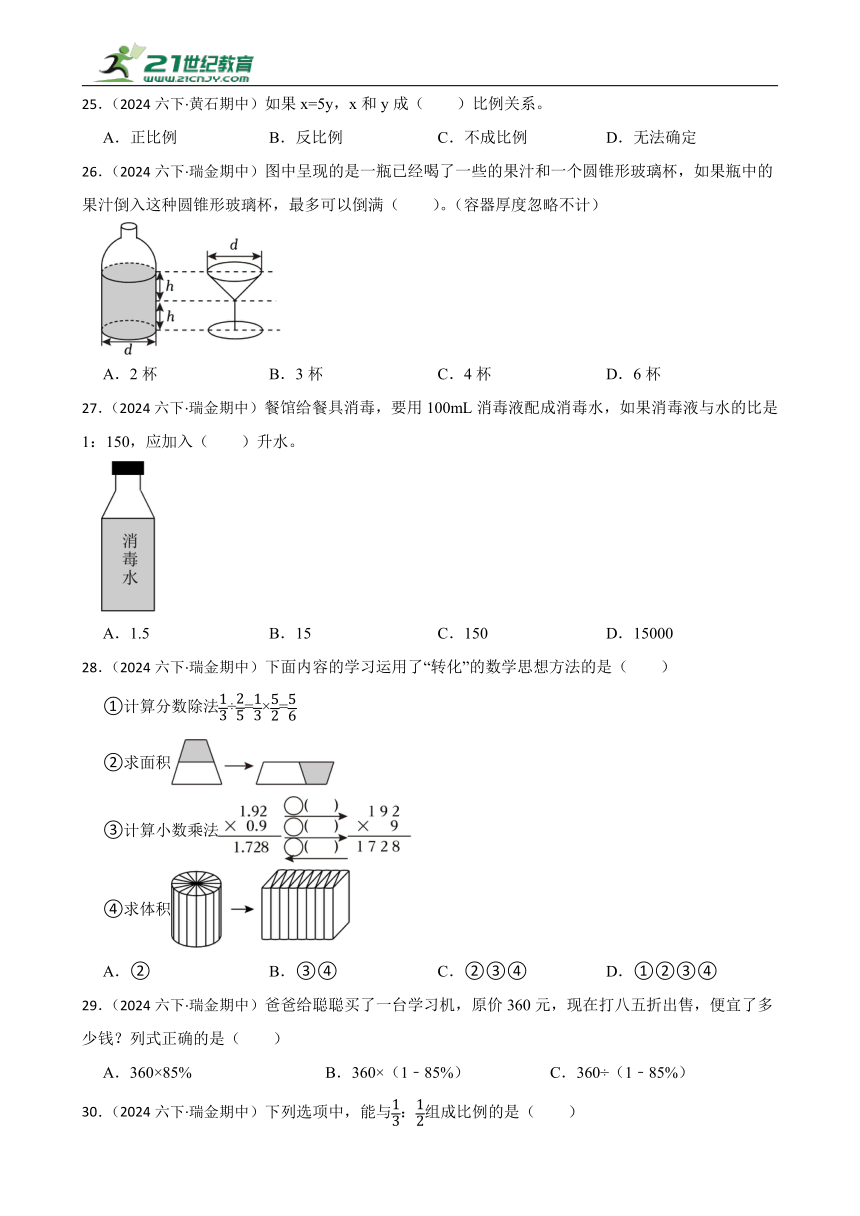
26.(2024六下·瑞金期中)图中呈现的是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯,如果瓶中的果汁倒入这种圆锥形玻璃杯,最多可以倒满( )。(容器厚度忽略不计)
A.2杯 B.3杯 C.4杯 D.6杯
27.(2024六下·瑞金期中)餐馆给餐具消毒,要用100mL消毒液配成消毒水,如果消毒液与水的比是1:150,应加入( )升水。
A.1.5 B.15 C.150 D.15000
28.(2024六下·瑞金期中)下面内容的学习运用了“转化”的数学思想方法的是( )
①计算分数除法÷=×=
②求面积
③计算小数乘法
④求体积
A.② B.③④ C.②③④ D.①②③④
29.(2024六下·瑞金期中)爸爸给聪聪买了一台学习机,原价360元,现在打八五折出售,便宜了多少钱?列式正确的是( )
A.360×85% B.360×(1﹣85%) C.360÷(1﹣85%)
30.(2024六下·瑞金期中)下列选项中,能与:组成比例的是( )
A.: B.3:2 C.0.2:0.3 D.:0.25
31.(2024六下·瑞金期中)小明买了一瓶水喝掉了一部分后还有剩余(如图所示),已知这个饮料瓶的内直径是6cm。根据如图中标出的数据,小明用算式“3.14×(6÷2)2×(18+7)”计算的是( )
A.喝掉的水的体积。
B.瓶子的容积。
C.剩余水的体积。
D.喝掉的水和剩余的水相差的体积。
32.(2024六下·瑞金期中)下面几组相关联的量中,成正比例关系的是( )。
A.总价一定,单价和数量。
B.正方体的底面积一定,体积和高。
C.圆的周长和半径。
D.儿童的年龄和身高。
33.(2024六下·瑞金期中)如下图所示,阴影部分表示某件商品优惠的价格,那么该商品是打( )
A.一折 B.五折 C.七五折 D.九折
34.(2024六下·瑞金期中)在百米赛跑中,运动员的比赛成绩跟风速有关。风速+1.3米/秒表示当时风速为顺风1.3米秒,﹣1.5米/秒表示( )
A.当时风速为逆风1.5米/秒 B.当时风速为顺风1.5米/秒
C.运动员的速度为1.5米/秒 D.当时风速为逆风0.2米/秒
35.(2024六下·玉田期中)压路机滚筒滚动一周能压多少路面是求滚筒的( )
A.表面积 B.侧面积 C.体积
36.(2024六下·陆川期中)下列各种关系中,不成正比例关系的是( )。
A.圆锥的体积一定,它的底面积和高
B.圆的周长和它的直径
C.实际距离一定,图上距离和比例尺
37.(2024六下·陆川期中)一种机器零件(如图),圆锥部分和圆柱部分的体积比是( )
A.1:6 B.1:3 C.1:4
38.(2024六下·陆川期中)如图,把一个直径为4cm,高为10cm的圆柱,沿底面直径切开,面积增加了多少平方厘米 答案正确的是( )
A.100.48 cm2 B. C.
39.(2024六下·陆川期中)一笔钱存两年,年利率是2.15%,到期时取得利息163.4元,这笔钱是( )元。
A.3800 B.760 C.7600
40.(2024六下·鹰潭期中)下面各题中,成正比例关系的是( )。
A.正方形的边长和面积
B.速度一定,路程和时间
C.长方形的长一定,它的宽和周长
D.圆柱的侧面积一定,底面周长和高
41.(2024六下·鹰潭期中)下面( )杯中的饮料最多。
A. B. C.
42.(2024六下·鹰潭期中)在一个数轴上,-3在-2的( )边。
A.左 B.右 C.无法确定
43.(2024六下·鹰潭期中)在-9、+、2.8、0、-4.9、-、+43、中,正数有( )个。
A.2 B.4 C.5
44.(2024六下·南昌期中)一个长方形操场长250m,宽200m,选用比例尺( )画出的平面图最大。
A.1:500 B.1:5000 C.1:50000 D.1:1000
45.(2024六下·南昌期中)商品按“每满100元减20元”优惠销售,在购物金额( )的情况下与“打八折”优惠销售的幅度相同。
A.比整百元大一点儿 B.比整百元小一点儿
C.是整百元 D.无法确定
46.(2024六下·南昌期中)一个圆柱和一个圆锥的底面直径相等,圆柱的高是圆锥的3倍,圆锥的体积是5立方分米,圆柱的体积是( )立方分米。
A.15 B.5 C.45 D.75
47.(2024六下·南昌期中)一个圆柱的侧面展开图是一个正方形,则这个圆柱的高与底面直径的比( )。
A.1:1 B.1:π C.π:1 D.1:2π
48.(2024六下·南昌期中)把一个底面半径为2分米,高为6分米的圆柱体木块削成一个最大的圆锥体,削去部分的体积是( )立方分米。
A.25.12 B.200.96 C.100.48 D.50.24
49.(2024六下·南昌期中)把改写成数值比例尺是( )。
A.1:30 B.3000000:1 C.1:9000000 D.1:3000000
答案解析部分
1.A
3:(3-1)=3:2
故答案为:A。
找准单位“1”在“比”字后面。基本音阶“商”的发音管比基本音阶“徵”的发音管短,根据这个条件,把“徵”的发音管当做单位“1”,平均分成3份,“商”的发音管少一份,就是2份。所以“徵”和“商”的发音管长度比是3份比2份,就是3:2。
2.A
解:因为《儿童阅读》单价一定,且总价÷书的本数=书的单价(一定),即商一定,所以总价与书的本数成正比例。
故答案为:A。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示。
3.C
解:12.56×3-12.56
=37.68-12.56
=25.12(cm3)
故答案为:C。
根据圆柱与圆锥体积的关系可知等底等高的圆柱的体积是圆锥体积的3倍,因此,圆锥的体积×倍数=圆柱的体积,圆锥的体积×倍数-圆锥的体积=比圆柱体积少的体积。
4.B
解:设圆柱的底面半径是r,高是h
原体积:πr2h
扩大后的体积:
π(3r)2(3h)=27πr2h,即体积扩大27倍。
故答案为:B。
圆柱的体积=圆周率×半径的平方×高,根据题意计算扩大后的圆柱体积再与原体积比较即可判断。
5.A
解:2×3.14×3=18.84(厘米)
底面周长和高相等,它的侧面展开图是正方形。
故答案为:A。
当底面周长和高相等时,圆柱的侧面展开图是一个正方形;当底面周长和高不相等时,圆柱的侧面展开图是一个长方形;当沿着侧面斜着剪开时,圆柱的侧面是一个平行四边形。
6.B
因为在比例中,两个外项互为倒数,
所以两个内项的积=1,
所以两个内项成反比例。
根据倒数的定义结合比例的基本性质,即可得出两个内项的关系。
故选:B
7.C
解:以3厘米为轴旋转一周,圆锥的底面半径是4厘米,高是3厘米,
圆锥的体积:3.14×4×4×3÷3=50.24(立方厘米)
以4厘米为轴旋转一周,圆锥的底面半径是3厘米,高是4厘米,
圆锥的体积:3.14×3×3×4÷3=37.68(立方厘米)
得到的图形的体积是37.68立方厘米或50.24立方厘米
故答案为:C。
π×底面半径的平方×高÷3=圆锥的体积。
8.A
解:A:0不是最小的整数,因为还有负整数,这些负整数都比0小,原题说法错误;
B:圆锥的侧面展开后是一个扇形,原题说法正确;
C:一个保温杯最多装水450毫升,说明它的容积是450毫升,原题说法正确。
故答案为:A。
正整数、0、负整数都是整数,据此解答。
9.C
解:用砖的总块数×每块砖的面积=铺地的面积(一定),
用砖的总块数和每块砖的面积成反比例。
故答案为:C。
反比例的判断方法:相关联,能变化,积一定。
10.A
解:16×3÷20=48÷20=2.4(厘米)
圆锥的高是2.4厘米。
故答案为:A。
圆锥的体积×3÷圆锥的底面积=圆锥的高。
11.C
解:圆柱的底面周长,也是侧面商标纸的长:3.14×8=25.12(厘米)
商标纸的宽等于圆柱的高,是12厘米,
长26厘米,宽12厘米的纸比较合适。
故答案为:C。
π×底面直径=底面周长,底面周长就是长方形的长,据此解答。
12.B
解:(3,5)表示第3列第5行,
A:(2,5)表示第2列第5行, 在小红的左面, 可能是她的同桌;
B:(3,4)表示第3列第4行,是前后桌, 一定不是她的同桌;
C:(4,5) 表示第4列第5行,在小红的右面, 可能是她的同桌。
故答案为:B。
数对的表示方法:先列后行。括号里的第一个数表示列数,第二个数表示行数,列数和行数相交的地方就是这个数对表示的位置。
13.B
解:A:圆的周长÷它的直径=π,圆的周长和它的直径成正比例。原题说法正确;
B:用去的米数+剩下的米数=彩带的总长度(一定),用去的米数和剩下的米数不成比例,原题说法错误;
C:比的前项÷后项=比值(一定),比的前项和后项成正比例。原题说法正确。
故答案为:B。
正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
14.A
解:500-5=495(克)
说明每袋盐的实际质量不低于495g。
故答案为:A。
“净重500±5g”表示最少500-5克,最多500+5克,这个范围内都属于合格。
15.C
16.C
解:A:男女运动员的和一定,参加马拉松的男运动员人数与女运动员人数不成比例关系;
B:速度×时间=路程(一定),因此小思参加了“欢乐跑”,她跑步的速度与时间成反比例关系;
C:学生总人数÷车的数量=一辆车乘坐的人数(一定),因此用相同的大巴车接送参加马拉松的学生,在每辆车坐满的情况下,接送学生的总人数与大巴车的数量成正比例关系;
D:开跑1小时后,李叔叔已经跑的路程与未跑的路程和一定,不成比例关系。
故答案为:C。
如果两个相关联的量比值一定,就成正比例,乘积一定就成反比例;由此即可判断。
17.D
18.B
19.A
20.A
21.B
解: 一个圆柱的侧面展开图是一个正方形,说明圆柱的底面周长和高相等,
圆柱的底面周长=π×底面直径,
这个圆柱的底面直径与高的比是::底面周长=:1=1:π
故答案为:B。
化简比的方法:根据比的基本性质,比的前项和后项同时乘以或除以同一个不为0的数,把比化为最简单的整数比。
22.A
解:6.39%读作百分之六点三九,这个6.39%叫百分数。
故答案为:A。
表示一个数是另一个数的百分之几的数叫作百分数。百分数也叫作百分率或百分比。
23.B
解:商品的原价看做单位1,
提价后的价格:1×(1+10%)=1.1,
再打九折后的价格:1.1×0.9=0.99,
1>0.99
现价比原价低 。
故答案为:B。
原价×(1+10%)=提价后的价格,提价后的价格×九折=再打九折后的价格,原价>再打九折后的价格,说明现价比原价低 。
24.D
解:已经看的页数+未看的页数=这本书的页数,
已经看的页数a与未看的页数b没有比例关系,有和一定的关系。
故答案为:D。
正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
25.A
解:由x=5y可得x÷y=5,x和y成正比例关系。
故答案为:A。
正比例的判断方法:相关联,能变化,商一定。
26.D
解:3×2=6(杯)
故答案为:D。
果汁瓶的底面直径和圆锥形玻璃杯杯口的直径相等,瓶中果汁的高度是2h,圆锥形玻璃杯中能装饮料的高度为h;等底等高的情况下,圆柱的体积是圆锥体积的3倍;据此计算出可以倒的杯数。
27.B
解:设应加入x毫升水。
100:x=1:150
x = 100×150
x=15000
15000毫升=15升。
故答案为:B。
设应加入x毫升水。依据消毒液的体积:加入水的体积=1:150,列比例,解比例,然后单位换算。
28.D
解:①把除法转化成乘法;②把平行四边形转化成长方形;③把小数乘法转化成整数乘法;④把圆柱转化成长方体来求体积。
故答案为:D。
①转化后把除法转化成乘法;②转化后面积不变,这样就能通过计算长方形的面积计算平行四边形面积;③计算小数乘法,把小数乘法转化成整数乘法,然后把小数点向左移动,这样就能计算小数乘法;④转化后体积不变,这样就能通过计算长方体的体积计算圆柱体积。
29.B
解:(1-85%)是便宜的钱数占原价的百分率,则便宜的钱数=360×(1﹣85%)。
故答案为:B。
便宜钱数=原价×(1-折扣)。
30.C
解::=÷=
A::=÷=,不能组成比例;
B:3:2=3÷2=,不能组成比例;
C:0.2:0.3=0.2÷0.3=,能组成比例;
D::0.25=÷0.25=,不能组成比例。
故答案为:C。
比例:表示两个比相等的式子叫做比例。分别计算出各个选项的比值,找到与:的比值相等的比即可。
31.B
解:“(6÷2)”是饮料瓶的内半径,“(18+7)”是喝掉水加剩下水的高度和,所以“3.14×(6÷2)2×(18+7)”计算的是饮料瓶的容积。
故答案为:B。
右边高度为18cm的圆柱的体积为喝掉水的体积,左边高度为7cm的圆柱的体积为剩下水的体积,两个的体积之和就是圆柱的容积。
32.C
A.因为数量×单价=总价(一定),两个数的乘积一定,所以单价和数量成反比例;
B.正方体的底面积一定,说明高和体积是个定值,不存在变量,所以高和体积不成比例;
C.圆的周长:半径=2,两个数的比值一定,所以圆的周长和半径成正比例;
D.儿童的年龄和身高不成比例。
故答案为:C。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量;
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。
33.C
解:图中阴影部分大约占了,空白部分则占1-=;
=75%=七五折
故答案为:该商品是打七五折出售的。
阴影部分为优惠的价格,则空白部分为折扣;几折就表示百分之几十;据此将空白部分占的分率改写成百分数,再化为折扣即可。
34.A
顺风为正,逆风为负,-1.5米秒表示逆风1.5米秒。
故答案为:A。
正数和负数是数学中用来表示具有相反意义的量的数值。正数通常表示增加、增长、盈余等,而负数则表示减少、下降、亏损等。
35.B
压路机滚筒滚动一周能压多少路面是求滚筒的侧面积。
故答案为:B。
压路机滚筒滚动一周压过的路面正是圆柱的侧面展开图,故是圆柱的侧面,求的是它的侧面积。
36.A
解:A:圆锥的底面积×高 =圆锥的体积×3(一定),它的底面积和高成反比例关系;
B:圆的周长÷它的直径=π(一定), 圆的周长和它的直径成正比例关系;
C:图上距离÷比例尺= 实际距离(一定),图上距离和比例尺成正比例关系。
故答案为:A。
正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
37.A
解:6÷3=2
1:(2×3)=1:6。
故答案为:A。
圆锥和圆柱的底面积相等,并且圆柱的高是圆锥高的2倍,则圆柱的体积是圆锥体积的3×2=6倍,则圆锥部分和圆柱部分的体积比是1:6。
38.B
解:4×10×2
=40×2
=80(平方厘米)。
故答案为:B。
增加的表面积=底面直径×高×增加面的个数。
39.A
解:163.4÷2÷2.15%
=81.7÷2.15%
=3800(元)
故答案为:A。
本金=年利息÷年利率,就此解答。
40.B
解:A:正方形边长和面积不成比例;
B:速度一定,路程和时间成正比例;
C :长方形的长一定,它的宽和周长不成比例;
D:圆柱的侧面积一定,底面周长和高成反比例。
故答案为:B。
A:正方形面积÷边长=边长,边长一定,面积就一定,二者不成比例;
B:路程÷时间=速度,速度一定,路程和时间成正比例;
C:长方形长+宽=周长÷2,长一定,宽和周长不成比例;
D:圆柱的底面周长×高=侧面积,所以底面周长和高成反比例。
41.B
解:的底面直径和高都大于,的饮料比的饮料多;的饮料比的饮料多,所以中饮料最多。
故答案为:B。
圆柱的体积=底面积×高,所以圆柱的容积大小与圆柱的底面直径和高有关,根据每个杯子中的底面直径和饮料的高度判断饮料的多少即可。
42.A
解:在一个数轴上,-3在-2的左边。
故答案为:A。
数轴上0左边的数是负数,右边的数是正数。越向左,数字越小,越向右,数字越大。
43.B
解:在-9、+、2.8、0、-4.9、-、+43、中,正数有+、2.8、+43、,共4个。
故答案为:B。
正负数表示相反意义的量,正数都带有“+”号或不带任何符号,负数都带有“-”号。0不是正数也不是负数。
44.A
解:250米=25000厘米,200米=20000厘米;
A:25000×=50(厘米),20000×=40(厘米),50×40=2000(平方厘米);
。
故答案为:A。
图上距离=比例尺×实际距离;据此求出长方形操场的图上长和宽,然后根据“长×宽”求出操场的图上面积,比较即可。
45.C
解:假设商品价格是120元,120-20=100元,;
假设商品价格是90元,;
假设商品价格为100元,100-20=80元,。
故答案为:C。
打八折是在原价的基础上乘以百分之八十。
46.C
解:
故答案为:C。
圆柱与圆锥的底面直径相等,则它们的底面积相等,圆锥体积=×底面积×圆锥的高,圆柱的高是圆锥的3倍,所以圆柱体积=底面积×圆柱的高=圆锥的体积÷×3。
47.C
解:圆柱的高:底面直径=πd:d=π:1。
故答案为:C。
由圆柱侧面展开图是一个正方形可知,圆柱的底面周长与圆柱的高相等,圆的周长=直径×π;根据比的意义化简比。
48.D
解:
故答案为:D
圆柱木块削成最大的圆锥,圆锥的底面半径=圆柱的底面半径;圆锥的高=圆柱的高;且等底等高的圆锥的体积=×圆柱的体积,所以削去部分的体积=圆柱的体积-圆锥的体积=圆柱的体积×。
49.D
解:30km=3000000cm,所以数值比例尺=1:30000000。
故答案为:D
1km=100000cm;图上距离与实际距离的比即为比例尺。
期中考试真题分类汇编01单项选择
一、单选题
1.(2024六下·蓬江期中)“宫、商、角、徵、羽”是我国古代音乐的基本音阶。基本音阶“商”的发音管比基本音阶“徵”的发音管短,则“徵”和“商”的发音管长度比是( )。
A.3:2 B.2:3 C.4:3 D.3:4
2.(2024六下·江门期中)购买儿童阅读这本书,总价与( )成正比例。
A.书的本数 B.书的页数 C.书的单价
3.(2024六下·江门期中)一个圆锥体积是 12.56cm3,比等底等商的圆柱体积少了( ) cm3
A.6.28 B.12.56 C.25.12
4.(2024六下·江门期中)一个圆柱的底面半径和高都扩大3倍,它的体积扩大( )倍。
A.9 B.27 C.6
5.(2024六下·江门期中)一个圆柱体的底面半径是3厘米,高是18.84厘米,它的侧面展开图是( )。
A.正方形
B.长方形
C.两个圆形和一个长方形组成
6.(2024六下·江门期中)在比例中,两个外项互为倒数,两个内项( )
A.成正比例 B.成反比例 C.不成比例
7.(2024六下·玉田期中)如下图所示,如果以一条直角边为轴旋转一周,得到的图形的体积是( )cm3。
A.37.68 B.50.24 C.37.68或50.24
8.(2024六下·玉田期中)下面说法错误的是( )
A.0是最小的整数。
B.圆锥的侧面展开后是一个扇形。
C.一个保温杯最多装水450毫升,说明它的容积是450毫升。
9.(2024六下·玉田期中)铺地的面积一定,用砖的总块数和每块砖的( )成反比例。
A.边长 B.周长 C.面积
10.(2024六下·玉田期中) 一个圆锥形零件,体积是16立方厘米,底面积是20平方厘米,它的高是( )厘米。
A.2.4 B.0.8 C.12.5
11.(2024六下·玉田期中)某工厂生产了一种饮料桶,尺寸如图所示。(单位:厘米)下面有三种饮料筒侧面的商标纸,你认为哪种纸比较合适?( )
A.
B.
C.
12.(2024六下·玉田期中)红红在数室里的位置用数对表示是(3,5),下面的数对中,( )表示的位置一定不是她的同桌。
A.(2,5) B.(3,4) C.(4,5)
13.(2024六下·玉田期中)关于正比例和反比例,说法错误的是( )
A.圆的周长和它的直径成正比例。
B.彩带的总长度一定,用去的米数和剩下的米数成反比例。
C.比值一定,比的前项和后项成正比例。
14.(2024六下·玉田期中)一袋食用盐上写着“净重500±5g”,说明每袋盐的实际质量不低于( )g。
A.495 B.500 C.505
15.(2024六下·柳州期中)小军将一根长10厘米的铁丝分成三段,再首尾相连组成一个三角形。下面图( )的方法一定能围成一个三角形。
A.
B.
C.
D.
16.(2024六下·柳州期中)下面是2024年柳州马拉松的信息,其中成正比例关系的是( )
A.参加马拉松的男运动员人数与女运动员人数。
B.小思参加了“欢乐跑”,她跑步的速度与时间。
C.用相同的大巴车接送参加马拉松的学生,在每辆车坐满的情况下,接送学生的总人数与大巴车的数量。
D.开跑1小时后,李叔叔已经跑的路程与未跑的路程。
17.(2024六下·柳州期中)数轴上有2个数,分别是E、F(如图)。下列式子结果最大的是( )
A.F+E B.F﹣E C.F×E D.F÷E
18.(2024六下·柳州期中)有3个连续奇数,其中最小的奇数是n,则这3个奇数的和是( )
A.3(n+1) B.3(n+2) C.3(n+6) D.3n
19.(2024六下·柳州期中)诗句“黄河远上白云间,一片孤城万仞山”中的“仞”在古代是一个长度单位,以周、秦、汉的度量衡来论,“一仞”就是八尺,一尺等于23.1厘米。那么“一仞”相当于( )
A.成年人的身高 B.成年人一臂的长度
C.成年人一掌的长度 D.成年人一拃的长度
20.(2024六下·柳州期中)为了研究“14亿粒米有多重”这个问题。六⑴班同学在数学活动课中进行了操作,其中第一小组数出200粒米,称得质量为4克,以此计算后得到14亿粒大米大约重( )吨。
A.28 B.56 C.5600 D.2.8
21.(2024六下·黄石期中) 一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是( )
A.1:2π B.1:π C.π:1 D.1:1
22.(2024六下·黄石期中)我国2023年的出生人口为902万人,出生率为6.39%。这个6.39%叫( )数。
A.百分数 B.千分数 C.万分数 D.都可以
23.(2024六下·黄石期中) 一种商品,先提价10%后,再打九折出售( )
A.比原价高 B.比原价低 C.与原价相同 D.无法确定
24.(2024六下·黄石期中)看一本书,已经看的页数a与未看的页数b是( )关系。
A.没有 B.正比例 C.反比例 D.和一定
25.(2024六下·黄石期中)如果x=5y,x和y成( )比例关系。
A.正比例 B.反比例 C.不成比例 D.无法确定
26.(2024六下·瑞金期中)图中呈现的是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯,如果瓶中的果汁倒入这种圆锥形玻璃杯,最多可以倒满( )。(容器厚度忽略不计)
A.2杯 B.3杯 C.4杯 D.6杯
27.(2024六下·瑞金期中)餐馆给餐具消毒,要用100mL消毒液配成消毒水,如果消毒液与水的比是1:150,应加入( )升水。
A.1.5 B.15 C.150 D.15000
28.(2024六下·瑞金期中)下面内容的学习运用了“转化”的数学思想方法的是( )
①计算分数除法÷=×=
②求面积
③计算小数乘法
④求体积
A.② B.③④ C.②③④ D.①②③④
29.(2024六下·瑞金期中)爸爸给聪聪买了一台学习机,原价360元,现在打八五折出售,便宜了多少钱?列式正确的是( )
A.360×85% B.360×(1﹣85%) C.360÷(1﹣85%)
30.(2024六下·瑞金期中)下列选项中,能与:组成比例的是( )
A.: B.3:2 C.0.2:0.3 D.:0.25
31.(2024六下·瑞金期中)小明买了一瓶水喝掉了一部分后还有剩余(如图所示),已知这个饮料瓶的内直径是6cm。根据如图中标出的数据,小明用算式“3.14×(6÷2)2×(18+7)”计算的是( )
A.喝掉的水的体积。
B.瓶子的容积。
C.剩余水的体积。
D.喝掉的水和剩余的水相差的体积。
32.(2024六下·瑞金期中)下面几组相关联的量中,成正比例关系的是( )。
A.总价一定,单价和数量。
B.正方体的底面积一定,体积和高。
C.圆的周长和半径。
D.儿童的年龄和身高。
33.(2024六下·瑞金期中)如下图所示,阴影部分表示某件商品优惠的价格,那么该商品是打( )
A.一折 B.五折 C.七五折 D.九折
34.(2024六下·瑞金期中)在百米赛跑中,运动员的比赛成绩跟风速有关。风速+1.3米/秒表示当时风速为顺风1.3米秒,﹣1.5米/秒表示( )
A.当时风速为逆风1.5米/秒 B.当时风速为顺风1.5米/秒
C.运动员的速度为1.5米/秒 D.当时风速为逆风0.2米/秒
35.(2024六下·玉田期中)压路机滚筒滚动一周能压多少路面是求滚筒的( )
A.表面积 B.侧面积 C.体积
36.(2024六下·陆川期中)下列各种关系中,不成正比例关系的是( )。
A.圆锥的体积一定,它的底面积和高
B.圆的周长和它的直径
C.实际距离一定,图上距离和比例尺
37.(2024六下·陆川期中)一种机器零件(如图),圆锥部分和圆柱部分的体积比是( )
A.1:6 B.1:3 C.1:4
38.(2024六下·陆川期中)如图,把一个直径为4cm,高为10cm的圆柱,沿底面直径切开,面积增加了多少平方厘米 答案正确的是( )
A.100.48 cm2 B. C.
39.(2024六下·陆川期中)一笔钱存两年,年利率是2.15%,到期时取得利息163.4元,这笔钱是( )元。
A.3800 B.760 C.7600
40.(2024六下·鹰潭期中)下面各题中,成正比例关系的是( )。
A.正方形的边长和面积
B.速度一定,路程和时间
C.长方形的长一定,它的宽和周长
D.圆柱的侧面积一定,底面周长和高
41.(2024六下·鹰潭期中)下面( )杯中的饮料最多。
A. B. C.
42.(2024六下·鹰潭期中)在一个数轴上,-3在-2的( )边。
A.左 B.右 C.无法确定
43.(2024六下·鹰潭期中)在-9、+、2.8、0、-4.9、-、+43、中,正数有( )个。
A.2 B.4 C.5
44.(2024六下·南昌期中)一个长方形操场长250m,宽200m,选用比例尺( )画出的平面图最大。
A.1:500 B.1:5000 C.1:50000 D.1:1000
45.(2024六下·南昌期中)商品按“每满100元减20元”优惠销售,在购物金额( )的情况下与“打八折”优惠销售的幅度相同。
A.比整百元大一点儿 B.比整百元小一点儿
C.是整百元 D.无法确定
46.(2024六下·南昌期中)一个圆柱和一个圆锥的底面直径相等,圆柱的高是圆锥的3倍,圆锥的体积是5立方分米,圆柱的体积是( )立方分米。
A.15 B.5 C.45 D.75
47.(2024六下·南昌期中)一个圆柱的侧面展开图是一个正方形,则这个圆柱的高与底面直径的比( )。
A.1:1 B.1:π C.π:1 D.1:2π
48.(2024六下·南昌期中)把一个底面半径为2分米,高为6分米的圆柱体木块削成一个最大的圆锥体,削去部分的体积是( )立方分米。
A.25.12 B.200.96 C.100.48 D.50.24
49.(2024六下·南昌期中)把改写成数值比例尺是( )。
A.1:30 B.3000000:1 C.1:9000000 D.1:3000000
答案解析部分
1.A
3:(3-1)=3:2
故答案为:A。
找准单位“1”在“比”字后面。基本音阶“商”的发音管比基本音阶“徵”的发音管短,根据这个条件,把“徵”的发音管当做单位“1”,平均分成3份,“商”的发音管少一份,就是2份。所以“徵”和“商”的发音管长度比是3份比2份,就是3:2。
2.A
解:因为《儿童阅读》单价一定,且总价÷书的本数=书的单价(一定),即商一定,所以总价与书的本数成正比例。
故答案为:A。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示。
3.C
解:12.56×3-12.56
=37.68-12.56
=25.12(cm3)
故答案为:C。
根据圆柱与圆锥体积的关系可知等底等高的圆柱的体积是圆锥体积的3倍,因此,圆锥的体积×倍数=圆柱的体积,圆锥的体积×倍数-圆锥的体积=比圆柱体积少的体积。
4.B
解:设圆柱的底面半径是r,高是h
原体积:πr2h
扩大后的体积:
π(3r)2(3h)=27πr2h,即体积扩大27倍。
故答案为:B。
圆柱的体积=圆周率×半径的平方×高,根据题意计算扩大后的圆柱体积再与原体积比较即可判断。
5.A
解:2×3.14×3=18.84(厘米)
底面周长和高相等,它的侧面展开图是正方形。
故答案为:A。
当底面周长和高相等时,圆柱的侧面展开图是一个正方形;当底面周长和高不相等时,圆柱的侧面展开图是一个长方形;当沿着侧面斜着剪开时,圆柱的侧面是一个平行四边形。
6.B
因为在比例中,两个外项互为倒数,
所以两个内项的积=1,
所以两个内项成反比例。
根据倒数的定义结合比例的基本性质,即可得出两个内项的关系。
故选:B
7.C
解:以3厘米为轴旋转一周,圆锥的底面半径是4厘米,高是3厘米,
圆锥的体积:3.14×4×4×3÷3=50.24(立方厘米)
以4厘米为轴旋转一周,圆锥的底面半径是3厘米,高是4厘米,
圆锥的体积:3.14×3×3×4÷3=37.68(立方厘米)
得到的图形的体积是37.68立方厘米或50.24立方厘米
故答案为:C。
π×底面半径的平方×高÷3=圆锥的体积。
8.A
解:A:0不是最小的整数,因为还有负整数,这些负整数都比0小,原题说法错误;
B:圆锥的侧面展开后是一个扇形,原题说法正确;
C:一个保温杯最多装水450毫升,说明它的容积是450毫升,原题说法正确。
故答案为:A。
正整数、0、负整数都是整数,据此解答。
9.C
解:用砖的总块数×每块砖的面积=铺地的面积(一定),
用砖的总块数和每块砖的面积成反比例。
故答案为:C。
反比例的判断方法:相关联,能变化,积一定。
10.A
解:16×3÷20=48÷20=2.4(厘米)
圆锥的高是2.4厘米。
故答案为:A。
圆锥的体积×3÷圆锥的底面积=圆锥的高。
11.C
解:圆柱的底面周长,也是侧面商标纸的长:3.14×8=25.12(厘米)
商标纸的宽等于圆柱的高,是12厘米,
长26厘米,宽12厘米的纸比较合适。
故答案为:C。
π×底面直径=底面周长,底面周长就是长方形的长,据此解答。
12.B
解:(3,5)表示第3列第5行,
A:(2,5)表示第2列第5行, 在小红的左面, 可能是她的同桌;
B:(3,4)表示第3列第4行,是前后桌, 一定不是她的同桌;
C:(4,5) 表示第4列第5行,在小红的右面, 可能是她的同桌。
故答案为:B。
数对的表示方法:先列后行。括号里的第一个数表示列数,第二个数表示行数,列数和行数相交的地方就是这个数对表示的位置。
13.B
解:A:圆的周长÷它的直径=π,圆的周长和它的直径成正比例。原题说法正确;
B:用去的米数+剩下的米数=彩带的总长度(一定),用去的米数和剩下的米数不成比例,原题说法错误;
C:比的前项÷后项=比值(一定),比的前项和后项成正比例。原题说法正确。
故答案为:B。
正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
14.A
解:500-5=495(克)
说明每袋盐的实际质量不低于495g。
故答案为:A。
“净重500±5g”表示最少500-5克,最多500+5克,这个范围内都属于合格。
15.C
16.C
解:A:男女运动员的和一定,参加马拉松的男运动员人数与女运动员人数不成比例关系;
B:速度×时间=路程(一定),因此小思参加了“欢乐跑”,她跑步的速度与时间成反比例关系;
C:学生总人数÷车的数量=一辆车乘坐的人数(一定),因此用相同的大巴车接送参加马拉松的学生,在每辆车坐满的情况下,接送学生的总人数与大巴车的数量成正比例关系;
D:开跑1小时后,李叔叔已经跑的路程与未跑的路程和一定,不成比例关系。
故答案为:C。
如果两个相关联的量比值一定,就成正比例,乘积一定就成反比例;由此即可判断。
17.D
18.B
19.A
20.A
21.B
解: 一个圆柱的侧面展开图是一个正方形,说明圆柱的底面周长和高相等,
圆柱的底面周长=π×底面直径,
这个圆柱的底面直径与高的比是::底面周长=:1=1:π
故答案为:B。
化简比的方法:根据比的基本性质,比的前项和后项同时乘以或除以同一个不为0的数,把比化为最简单的整数比。
22.A
解:6.39%读作百分之六点三九,这个6.39%叫百分数。
故答案为:A。
表示一个数是另一个数的百分之几的数叫作百分数。百分数也叫作百分率或百分比。
23.B
解:商品的原价看做单位1,
提价后的价格:1×(1+10%)=1.1,
再打九折后的价格:1.1×0.9=0.99,
1>0.99
现价比原价低 。
故答案为:B。
原价×(1+10%)=提价后的价格,提价后的价格×九折=再打九折后的价格,原价>再打九折后的价格,说明现价比原价低 。
24.D
解:已经看的页数+未看的页数=这本书的页数,
已经看的页数a与未看的页数b没有比例关系,有和一定的关系。
故答案为:D。
正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
25.A
解:由x=5y可得x÷y=5,x和y成正比例关系。
故答案为:A。
正比例的判断方法:相关联,能变化,商一定。
26.D
解:3×2=6(杯)
故答案为:D。
果汁瓶的底面直径和圆锥形玻璃杯杯口的直径相等,瓶中果汁的高度是2h,圆锥形玻璃杯中能装饮料的高度为h;等底等高的情况下,圆柱的体积是圆锥体积的3倍;据此计算出可以倒的杯数。
27.B
解:设应加入x毫升水。
100:x=1:150
x = 100×150
x=15000
15000毫升=15升。
故答案为:B。
设应加入x毫升水。依据消毒液的体积:加入水的体积=1:150,列比例,解比例,然后单位换算。
28.D
解:①把除法转化成乘法;②把平行四边形转化成长方形;③把小数乘法转化成整数乘法;④把圆柱转化成长方体来求体积。
故答案为:D。
①转化后把除法转化成乘法;②转化后面积不变,这样就能通过计算长方形的面积计算平行四边形面积;③计算小数乘法,把小数乘法转化成整数乘法,然后把小数点向左移动,这样就能计算小数乘法;④转化后体积不变,这样就能通过计算长方体的体积计算圆柱体积。
29.B
解:(1-85%)是便宜的钱数占原价的百分率,则便宜的钱数=360×(1﹣85%)。
故答案为:B。
便宜钱数=原价×(1-折扣)。
30.C
解::=÷=
A::=÷=,不能组成比例;
B:3:2=3÷2=,不能组成比例;
C:0.2:0.3=0.2÷0.3=,能组成比例;
D::0.25=÷0.25=,不能组成比例。
故答案为:C。
比例:表示两个比相等的式子叫做比例。分别计算出各个选项的比值,找到与:的比值相等的比即可。
31.B
解:“(6÷2)”是饮料瓶的内半径,“(18+7)”是喝掉水加剩下水的高度和,所以“3.14×(6÷2)2×(18+7)”计算的是饮料瓶的容积。
故答案为:B。
右边高度为18cm的圆柱的体积为喝掉水的体积,左边高度为7cm的圆柱的体积为剩下水的体积,两个的体积之和就是圆柱的容积。
32.C
A.因为数量×单价=总价(一定),两个数的乘积一定,所以单价和数量成反比例;
B.正方体的底面积一定,说明高和体积是个定值,不存在变量,所以高和体积不成比例;
C.圆的周长:半径=2,两个数的比值一定,所以圆的周长和半径成正比例;
D.儿童的年龄和身高不成比例。
故答案为:C。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量;
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。
33.C
解:图中阴影部分大约占了,空白部分则占1-=;
=75%=七五折
故答案为:该商品是打七五折出售的。
阴影部分为优惠的价格,则空白部分为折扣;几折就表示百分之几十;据此将空白部分占的分率改写成百分数,再化为折扣即可。
34.A
顺风为正,逆风为负,-1.5米秒表示逆风1.5米秒。
故答案为:A。
正数和负数是数学中用来表示具有相反意义的量的数值。正数通常表示增加、增长、盈余等,而负数则表示减少、下降、亏损等。
35.B
压路机滚筒滚动一周能压多少路面是求滚筒的侧面积。
故答案为:B。
压路机滚筒滚动一周压过的路面正是圆柱的侧面展开图,故是圆柱的侧面,求的是它的侧面积。
36.A
解:A:圆锥的底面积×高 =圆锥的体积×3(一定),它的底面积和高成反比例关系;
B:圆的周长÷它的直径=π(一定), 圆的周长和它的直径成正比例关系;
C:图上距离÷比例尺= 实际距离(一定),图上距离和比例尺成正比例关系。
故答案为:A。
正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
37.A
解:6÷3=2
1:(2×3)=1:6。
故答案为:A。
圆锥和圆柱的底面积相等,并且圆柱的高是圆锥高的2倍,则圆柱的体积是圆锥体积的3×2=6倍,则圆锥部分和圆柱部分的体积比是1:6。
38.B
解:4×10×2
=40×2
=80(平方厘米)。
故答案为:B。
增加的表面积=底面直径×高×增加面的个数。
39.A
解:163.4÷2÷2.15%
=81.7÷2.15%
=3800(元)
故答案为:A。
本金=年利息÷年利率,就此解答。
40.B
解:A:正方形边长和面积不成比例;
B:速度一定,路程和时间成正比例;
C :长方形的长一定,它的宽和周长不成比例;
D:圆柱的侧面积一定,底面周长和高成反比例。
故答案为:B。
A:正方形面积÷边长=边长,边长一定,面积就一定,二者不成比例;
B:路程÷时间=速度,速度一定,路程和时间成正比例;
C:长方形长+宽=周长÷2,长一定,宽和周长不成比例;
D:圆柱的底面周长×高=侧面积,所以底面周长和高成反比例。
41.B
解:的底面直径和高都大于,的饮料比的饮料多;的饮料比的饮料多,所以中饮料最多。
故答案为:B。
圆柱的体积=底面积×高,所以圆柱的容积大小与圆柱的底面直径和高有关,根据每个杯子中的底面直径和饮料的高度判断饮料的多少即可。
42.A
解:在一个数轴上,-3在-2的左边。
故答案为:A。
数轴上0左边的数是负数,右边的数是正数。越向左,数字越小,越向右,数字越大。
43.B
解:在-9、+、2.8、0、-4.9、-、+43、中,正数有+、2.8、+43、,共4个。
故答案为:B。
正负数表示相反意义的量,正数都带有“+”号或不带任何符号,负数都带有“-”号。0不是正数也不是负数。
44.A
解:250米=25000厘米,200米=20000厘米;
A:25000×=50(厘米),20000×=40(厘米),50×40=2000(平方厘米);
。
故答案为:A。
图上距离=比例尺×实际距离;据此求出长方形操场的图上长和宽,然后根据“长×宽”求出操场的图上面积,比较即可。
45.C
解:假设商品价格是120元,120-20=100元,;
假设商品价格是90元,;
假设商品价格为100元,100-20=80元,。
故答案为:C。
打八折是在原价的基础上乘以百分之八十。
46.C
解:
故答案为:C。
圆柱与圆锥的底面直径相等,则它们的底面积相等,圆锥体积=×底面积×圆锥的高,圆柱的高是圆锥的3倍,所以圆柱体积=底面积×圆柱的高=圆锥的体积÷×3。
47.C
解:圆柱的高:底面直径=πd:d=π:1。
故答案为:C。
由圆柱侧面展开图是一个正方形可知,圆柱的底面周长与圆柱的高相等,圆的周长=直径×π;根据比的意义化简比。
48.D
解:
故答案为:D
圆柱木块削成最大的圆锥,圆锥的底面半径=圆柱的底面半径;圆锥的高=圆柱的高;且等底等高的圆锥的体积=×圆柱的体积,所以削去部分的体积=圆柱的体积-圆锥的体积=圆柱的体积×。
49.D
解:30km=3000000cm,所以数值比例尺=1:30000000。
故答案为:D
1km=100000cm;图上距离与实际距离的比即为比例尺。
同课章节目录
