期中考试真题分类汇编04单项选择(含答案+解析)---2024-2025学年北师大版六年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编04单项选择(含答案+解析)---2024-2025学年北师大版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 306.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 08:16:07 | ||
图片预览




文档简介
2024-2025学年北师大版六年级数学下册
期中考试真题分类汇编04单项选择
一、单选题
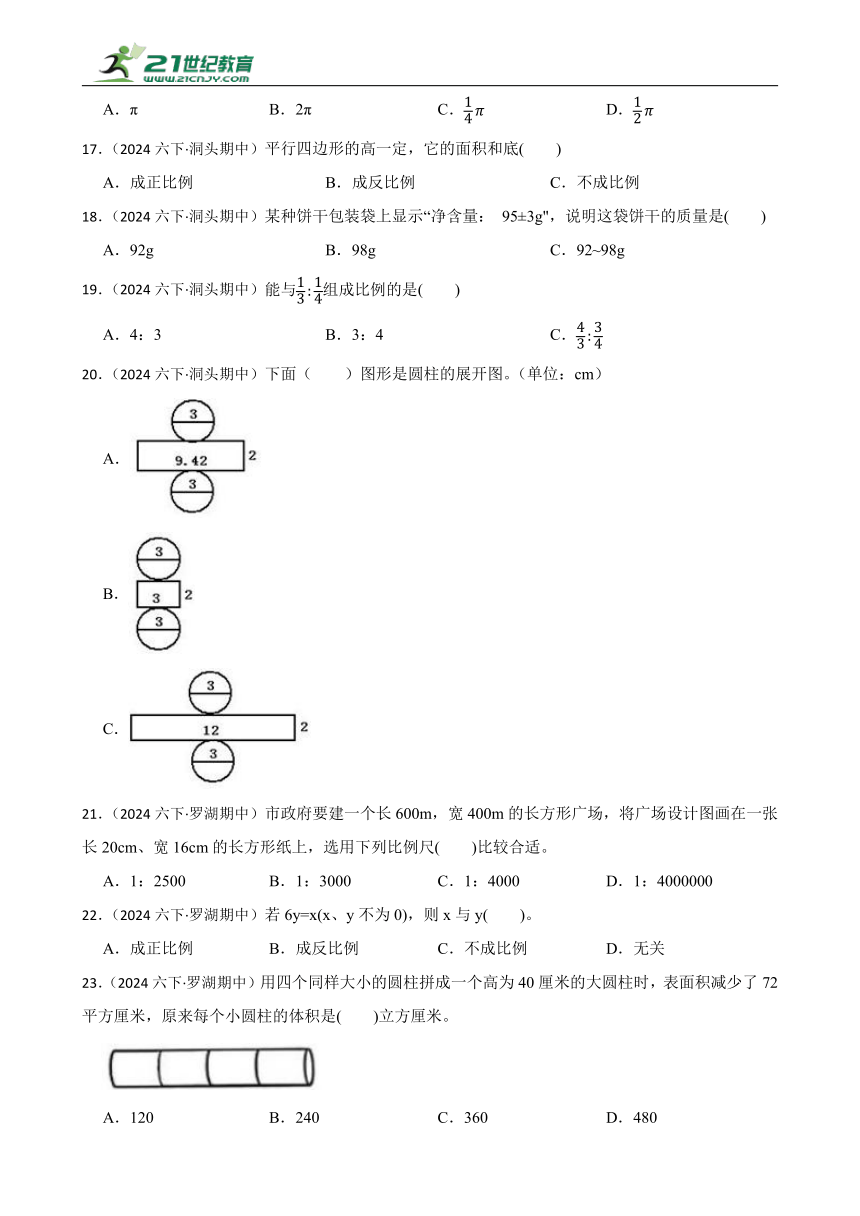
1.(2024六下·龙岗期中)丽丽做了一个底面直径是9厘米,高是15厘米的圆柱形的笔筒,她把笔筒高度的以下部分涂上颜色(底面不涂),涂颜色部分的面积是( ) 平方厘米。
A.282.6 B.254.34 C.169.56 D.423.9
2.(2024六下·龙岗期中)雪糕厂制作了底面积相同的三种模具(如下图),倒入同一种雪糕原浆,三种模具装的原浆相比较,( )。
A.正方体多 B.长方体多 C.圆柱多 D.一样多
3.(2024六下·龙岗期中)如下图,一个长方形的长为a,宽为b,分别以长,宽为轴旋转一周,产生了甲、乙两个圆柱。判断甲,乙两个圆柱侧面积的大小关系,( )。
A.甲>乙 B.甲<乙 C.甲=乙 D.无法比较
4.(2024六下·龙岗期中)一个圆柱的高是2dm,沿底面直径切开,横截面是一个正方形,下面说法错误的是( )。
A.这个圆柱的底面半径是1dm
B.这个圆柱的底面面积是3.14 dm2
C.这个圆柱的体积是6.28 dm3
D.这个圆柱切开后表面积增加4 dm2
5.(2024六下·龙岗期中)将一个电话号码牌绕点O逆时针旋转180°后如下图所示,这个电话号码是( )。
A.9916089 B.6616089 C.6619089 D.6806199
6.(2024六下·龙岗期中)把一根圆柱形木料削成一个最大的圆锥,削去部分体积是圆锥的( )。
A.2倍 B. C. D.
7.(2024六下·龙岗期中)如果x和y (x、y均不为0)是两种相关联的量,那么下面表示x和y成正比例关系的是( )。
A.x-y B.y+x C. D.
8.(2024六下·龙岗期中)与线段比例尺大小相同的比例尺是( )。
A.1:2000000 B.1:20 C.1:4000000 D.20:1
9.(2024六下·龙岗期中)在出勤率、出勤人数、全班人数这三个量中,当( )一定时, 另外两个量成反比例。
A.全班人数 B.出勤人数 C.出勤率 D.以上都可以
10.(2024六下·龙岗期中)在下面各比中,与能组成比例的是( )。
A.5 :2 B.2:5 C.:2 D.2:
11.(2024六下·龙岗期中)在下图中,以直线为轴旋转一周,可以得到圆锥的是( )。
A. B. C. D.
12.(2024六下·湛江期中)下列关系中,能表示a和b成反比例的是( )(a、b均不为0)。
A.a+b=5 B.a-b=5 C.= 5 D. =
13.(2024六下·湛江期中)圆柱的底面半径扩大3倍,高不变,它的体积扩大( )。
A.3倍 B.6倍 C.9倍 D.不变
14.(2024六下·湛江期中) 一幅地图的比例尺是1 : 5000000,地图上的1厘米表示实际距离( )。
A.50千米 B.500千米 C.5000千米 D.5000000千米
15.(2024六下·洞头期中)比例尺是1:5000000表示地图上1cm距离相当于实际距离( )
A.50m B.50km C.5km
16.(2024六下·洞头期中)一个圆柱的侧面展开图是一个正方形,这个圆柱的高是底面直径的( ) 倍。
A.π B.2π C. D.
17.(2024六下·洞头期中)平行四边形的高一定,它的面积和底( )
A.成正比例 B.成反比例 C.不成比例
18.(2024六下·洞头期中)某种饼干包装袋上显示“净含量: 95±3g",说明这袋饼干的质量是( )
A.92g B.98g C.92~98g
19.(2024六下·洞头期中)能与组成比例的是( )
A.4:3 B.3:4 C.
20.(2024六下·洞头期中)下面( )图形是圆柱的展开图。(单位:cm)
A.
B.
C.
21.(2024六下·罗湖期中)市政府要建一个长600m,宽400m的长方形广场,将广场设计图画在一张长20cm、宽16cm的长方形纸上,选用下列比例尺( )比较合适。
A.1:2500 B.1:3000 C.1:4000 D.1:4000000
22.(2024六下·罗湖期中)若6y=x(x、y不为0),则x与y( )。
A.成正比例 B.成反比例 C.不成比例 D.无关
23.(2024六下·罗湖期中)用四个同样大小的圆柱拼成一个高为40厘米的大圆柱时,表面积减少了72平方厘米,原来每个小圆柱的体积是( )立方厘米。
A.120 B.240 C.360 D.480
24.(2024六下·罗湖期中)如果正方体、圆柱、圆锥的底面积相等,高也相等。下面说法正确的是( )。
A.正方体的体积最大 B.圆柱的体积是圆锥的
C.圆锥的体积是正方体的 D.圆柱和正方体的表面积相同
25.(2024六下·罗湖期中)能通过下图的箭头旋转得到的是( )。
A. B. C. D.
26.(2024六下·罗湖期中)下图4个圆柱中,与圆锥的体积相等的是( )。
A.A B.B C.C D.D
27.(2024六下·罗湖期中)已知a÷=b×0.4,那么a:b=( )。
A.3:5 B.5:3 C.4:15 D.15:4
28.(2024六下·期中)把圆锥切一刀,切面不可能是( )。
A.三角形 B.椭圆形 C.平行四边形
29.(2024六下·期中)把高是15cm圆锥形容器盛满水,将水倒入等底等高的圆柱形容器,水面高是( )cm。
A.15 B.30 C.5
30.(2024六下·期中) 一幅地图的比例尺是20:1,如果零件图上长5厘米,则实际长( )。
A.4厘米 B.100厘米 C.0.25厘米
31.(2024六下·期中)如下图,柱形瓶底的面积与锥形瓶口的面积相等,将柱形瓶中的饮料倒入锥形瓶中,可以倒满( )杯。
A.2 B.3 C.6
32.(2024六下·盐都期中) 有两支蜡烛,当第一支燃去,第二支燃去时,剩下的部分一样长,第一支 蜡烛与第二支蜡烛原来长度的比是( )
A.6:5 B.5:3 C.2:1 D.3:5
33.(2024六下·盐都期中)体育活动室里,有 10 张乒乓球桌同时进行乒乓球比赛,双打的比单打的多 4 人, 进行双打比赛的乒乓球桌有( )张。
A.6 B.5 C.4 D.3
34.(2024六下·盐都期中)一个圆柱和一个圆锥的体积之比是 3︰4,底面积之比是 4︰3,高的比是 ( )。
A.3︰16 B.1︰3 C.9︰16 D.16︰9
35.(2024六下·盐都期中) 一个圆柱体和一个正方体底面周长和高分别相等,那么圆柱体的体积和正方 体的体积比较( )。
A.正方体大 B.圆柱体大 C.一样大 D.无法比较
36.(2024六下·盐都期中)把一张长方形照片按 1:10 的比例缩小,长与宽的比是( )。
A.不变 B.变了 C.10:1 D.1:10
37.(2024六下·盐都期中)根据 a:8=b:3 写出的比例,正确的是( )
A.a:b=3:8 B.8:a=b:3 C.3:8=b:a D.a:3=b:8
38.(2024六下·龙岗期中)一年一度的科技节正如火如荼的进行中,如图是乐乐参加比赛制作的火箭模型,其体积是( )
A.125.6cm3 B.100.48cm3 C.150.72cm3 D.200.96cm3
39.(2024六下·龙岗期中)为了推进体育强国建设,增强青少年体质,深圳市某小学新建一个长50m,宽20m的恒温游泳池,选用比例尺( )画出来的平面图面积最大。
A.1:1000 B.1:1500 C.1:500 D.1:100
40.(2024六下·龙岗期中)如图,沿直线MN旋转一周后,甲、乙两部分所形成的立体图形的体积比是( )
A.1:2 B.1:3 C.1:6 D.1:9
41.(2024六下·龙岗期中)端午节时,乐乐做了一个底面直径为4cm,高为8cm的圆柱形粽子,现在她要在粽子的侧面沾上一层糖,粽子沾糖的面积是( )cm2。
A.200.96 B.100.48 C.401.92 D.125.6
42.(2024六下·龙岗期中)博物馆的建筑设计有很多圆柱形的柱子支撑屋顶,工程翻新时打算给这些柱子刷油漆,刷油漆的面积指的是这些柱子的( )
A.表面积 B.体积 C.侧面积 D.底面积
43.(2024六下·龙岗期中)下列选项中,两个量不成反比例的是( )
A.乐乐放学回家,已走的路程和剩下的路程。
B.等分一块蛋糕,每个人分到的蛋糕大小与人数。
C.长方形的面积一定,它的长和宽。
D.百米赛跑,跑步的速度和时间。
44.(2024六下·龙岗期中)如图的图形绕虚线旋转一周得到的图形的表面积是( )cm2。
A.50.24 B.75.36 C.12.56 D.100.48
45.(2024六下·龙岗期中)如果一个圆柱的底面半径缩小到原来的,高扩大到原来的2倍,那么体积( )
A.缩小到原来的。 B.扩大到原来的2倍。
C.缩小到原来的。 D.没有变化。
46.(2024六下·龙岗期中)学校小操场内部要进行美化,现收集学生的作品。长方形操场的长和宽是27m和15m,按1:300的比缩小,则缩小后的长和宽是( )
A.9cm和5cm B.9m和5m
C.90cm和50cm D.8100cm和4500cm
47.(2024六下·龙岗期中)2023年2月3日,我国首条设计时速为每小时350千米的跨海高铁——福厦高铁进入静态验收阶段,全长300千米,笑笑画了6cm的路线图,请问笑笑用的比例尺是( )
A.1:7000000 B.1:5000000 C.1:50 D.5000000:1
48.(2024六下·龙岗期中)下列选项中,两个量不成正比例的是( )
A.圆锥的底面积一定,高和体积。
B.一根铁丝,用去部分和剩下部分。
C.单价一定,总价和数量。
D.速度不变,路程和时间。
49.(2024六下·龙岗期中)下面( )组的两个比可以组成比例。
A.1.2:1.3和4:5 B.:5和:4
C.:4和3:12 D.1.5:1.2和5:4
50.(2024六下·龙岗期中)2024年粤港澳大湾区深圳花展在仙湖植物园如期举行,本次花展使用的宣传海报的比例尺是,改写成数值比例尺是( )
A.1:8000 B.1:2000 C.2000:1 D.1:20
答案解析部分
1.C
解:9×3.14×15×
=28.26×6
=169.56(平方厘米)。
故答案为:C。
涂颜色部分的面积=侧面积×涂色部分的高度,其中,侧面积=π×直径×高。
2.D
解:三个立体图形的体积都是:底面积×高,则体积相等。
故答案为:D。
圆柱的体积=长方体的体积=正方体的体积=底面积×高,因为底面积、高都相等, 则体积也相等。
3.C
解:甲:2×π×b×a=2πab;
乙:2×π×a×b=2πab;
甲=乙。
故答案为:C。
圆柱的侧面积=2π×半径×高,然后比较大小。
4.D
解:A项:2÷2=1(分米),原题干说法正确;
B项:3.14×12=3.14(平方分米),原题干说法正确;
C项:3.14×12×2=6.28(立方分米),原题干说法正确;
D项:2×2×2=8(平方分米),原题干说法错误。
故答案为:D。
A项:这个圆柱的底面半径=直径÷2,其中,直径=圆柱的高;
B项:这个圆柱的底面积=π×半径2,
C项:这个圆柱的体积=底面积×高;
D项:这个圆柱切开后增加的表面积=底面直径×高×2。
5.C
解:这个电话号码变成了。
故答案为:C。
将这个个电话号码牌绕点O逆时针旋转180°如图所示,这个电话号码变成6619089。
6.A
解:(1-)÷
=÷
=2。
故答案为:A。
把一根圆柱形木料削成一个最大的圆锥,圆锥的体积是圆柱的,削去部分体积是圆锥体积的分率=(1-圆锥的体积)÷圆锥的体积。
7.C
解:A项:x和y不成比例;
B项:x和y不成比例;
C项:=(一定),x和y成正比例;
D项:xy=(一定),x和y反正比例。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
8.A
解:1:(20×100000)=1:2000000。
故答案为:A。
先单位换算20千米=2000000厘米,比例尺=图上距离÷实际距离。
9.B
解:全班人数×出勤率=出勤人数(一定),当出勤人数一定时, 另外两个量成反比例。
故答案为:B。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
10.A
解:×2=1,×5=1,所以:=5:2。
故答案为:A。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此判断。
11.C
解:直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
故答案为:C。
直角三角形的有两条直角边,依据圆锥的特点,直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
12.D
解:由 =可以化为a×b=3×5,即:a×b=15,a和b成反比例关系。
故答案为:D。
反比例的判断方法:相关联,能变化,积一定。
13.C
解:底面半径扩大3倍,底面积扩大9倍;
底面积扩大9倍,高不变,它的体积扩大9倍。
故答案为:C。
圆的半径、直径、周长扩大的倍数相等,面积扩大的倍数是他们的平方倍;如果高不变,圆锥体积扩大的倍数也是他们的平方倍。
14.A
解:5000000厘米=50000米=50千米,
地图上的1厘米表示实际距离50千米。
故答案为:A。
厘米去掉2个0化为米,米去掉3个0化为千米,据此解答。
15.B
解:1÷÷100000
=5000000÷100000
=50(千米)。
故答案为:B。
实际距离=图上距离÷比例尺,然后单位换算。
16.A
解:底面周长=π×直径,底面周长÷直径=π。
故答案为:A。
一个圆柱的侧面展开图是一个正方形,这个圆柱的高等于底面周长,高是底面直径的π倍。
17.A
解:平行四边形的面积÷底=高(一定),平行四边形的高一定,它的面积和底成正比例。
故答案为:A。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
18.C
解:95-3=92(克),95+3=98(克),说明这袋饼干的质量是92~98克。
故答案为:C。
净含量: 95±3g表示最少的质量=95-3=92克,最多的质量=95+3=98克。
19.A
解:×3=1,×4=1,则可以组成比例:4=:3。
故答案为:A。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此判断。
20.A
解:A、3.14×3=9.42(cm),底面周长与长方形的长相等,是圆柱的展开图;
B、3.14×3=9.42(cm),底面周长与长方形的长不相等,不是圆柱的展开图;
C、底面周长与长方形的长不相等,不是圆柱的展开图。
故答案为:A。
圆柱的侧面积沿着一条高展开后是一个长方形,长方形的长与圆柱的底面周长相等,计算出底面周长再与长方形的长比较后即可判断。
21.C
解:600m=60000cm,400m=40000cm
选项A:长:60000×=24(cm),宽:40000×=160(cm),24>20,16=16,不合适;
选项B:长:60000×=20(cm),宽:40000×=(cm),20=20,<16,但是不是整数,不合适;
选项C:长:60000×=15(cm),宽:40000×=10(cm),15<20,10<16,合适;
选项D:长:60000×=0.015(cm),宽:40000×=0.01(cm),0.015与0.01过于小,不合适;
故答案为:C。
根据图上距离=实际距离×比例尺,分别计算出按照各个比例尺画的图上长度,选择合适的即可。
22.A
解:若6y=x,则x÷y=6(一定),比值一定,x和y成正比例。
故答案为:A。
两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,则这两种量成正比例关系;如果这两种量的乘积一定,则这两种量成反比例关系。
23.A
解:72÷6×(40÷4)
=12×10
=120(立方厘米);
故答案为:A。
减少的表面积是6个底面积,因此,用减少的表面积除以6求出底面积,再根据圆柱体积=底面积×高,代入数值计算即可。
24.C
解:圆柱的体积=正方体的体积,圆锥的体积=圆柱的体积=正方体的体积;
故答案为:C。
正方体与圆柱的体积都是底面积乘高,因此,等底等高的情况下,圆柱与正方体的体积相等;圆锥的体积是与它等底等高的圆柱体积的;据此解答。
25.D
解:将该图形顺时针旋转90°、180°、270°,得到的图形依次是:、、;
故答案为:D。
将已知图形顺时针旋转90°、180°、270°,得到的图形与各个选项比较即可。
26.C
解:选项A:该圆柱与圆锥等底等高,所以它的体积是圆锥体积的3倍;
选项B:该圆柱与圆锥等高,底面积是圆锥的,所以它的体积是圆锥体积的;
选项C:该圆柱与圆锥等底,高是圆锥的,所以它的体积与圆锥的体积相等;
选项D:该圆锥的高是圆锥的,底面积是圆锥的,所以它的体积是圆锥体积的;
故答案为:C。
等底等高的圆柱体积是圆锥体积的3倍,因此,圆柱与圆锥的体积和高相等时,圆锥的底面积是圆柱的3倍;当圆柱与圆锥的体积和底面积相等时,圆锥的高是圆柱的3倍;据此解答。
27.C
解:a÷=a×,即a×=b×0.4,所以a:b=0.4:=4:15;
故答案为:C。
根据比例的基本性质:内项积等于外项,将其改写成比例的形式,再化简比即可。
28.C
解:把圆锥沿着顶点到底面直径切一刀,切面是三角形,沿着圆锥的一侧切一刀,切面是椭圆形,不可能是平行四边形。
故答案为:C。
圆锥有一个圆形的底面和一个曲面,把圆锥切一刀,切面不可能是平行四边形。
29.C
解:15÷3=5(厘米)。
故答案为:C。
等底等高的圆柱的体积是圆锥体积的3倍,圆柱形容器水面的高度=圆锥的高÷3。
30.C
解:5÷20=0.25(厘米)。
故答案为:C。
实际距离=图上距离÷比例尺。
31.C
解:3×2=6(杯)。
故答案为:C。
等底等高的圆柱的体积是圆锥体积的3倍,圆柱的高是圆锥高的2倍,底面积相等,则将柱形瓶中的饮料倒入锥形瓶中,可以倒满6杯。
32.B
解:第一支原来的长度×(1-)=第二支原来的长度×(1-),所以第一支原来的长度:第二支原来的长度=(1-):(1-)=:=5:3;
故答案为:B。
由题意可知,第一支剩下的长度=第一支原来的长度×(1-),第二支剩下的长度=第二支原来的长度×(1-),两支剩下的部分一样长,即第一支原来的长度×(1-)=第二支原来的长度×(1-),再根据比的基本性质:内项积等于外项积,即可求出第一支蜡烛与第二支蜡烛原来长度的比。
33.C
解:设进行双打比赛的乒乓球桌有x张,则进行单打比赛的乒乓球桌有(10-x)张。
4x-2×(10-x)=4
4x-20+2x=4
6x=24
x=4
故答案为:4。
可以设进行双打比赛的乒乓球桌有x张,则进行单打比赛的乒乓球桌有(10-x)张,题中的等量关系是:双打总人数-单打总人数=4,据此列方程解答。
34.A
解:假设圆柱和圆锥的体积分别是3和4,底面积分别是4和3;
圆柱的高:3÷4=;
圆锥的高:4×3÷3=4;
高的比是::4=3:16;
故答案为:A。
假设圆柱和圆锥的体积分别是3和4,底面积分别是4和3;根据圆柱的高=体积÷底面积,圆锥的高=体积×3÷底面积,分别求出圆柱和圆锥的高,再求出高的比。
35.B
解:周长相等的情况下,圆的面积大于正方形面积,即圆柱的底面积>正方形底面积,又因为它们的高相等,所以圆柱的底面积×高>正方形的底面积×高,圆柱的体积>正方体的体积。
故答案为:B。
周长相等的情况下,圆的面积大于正方形面积,根据圆柱体积=底面积×高,正方形体积=底面积×高,即可比较两个体积的大小。
36.A
解:原来长与宽的比是:长:宽;
缩小后的长与宽的比是:长:宽=长:宽;
因此,长与宽的比不变;
故答案为:A。
按照1:10的比例缩小,即长方形缩小后的长为原来长的,长方形缩小后的宽为原来宽的,据此解答。
37.C
解:根据a:8=b:3,可得:8b=3a;
选项A:根据a:b=3:8,可得3b=8a,不符合8b=3a,错误;
选项B:根据8:a=b:3,可得ab=8×3,不符合8b=3a,错误;
选项C:根据3:8=b:a,可得8b=3a,符合8b=3a,正确;
选项D:根据a:3=b:8,可得3b=8a,不符合8b=3a,错误;
故答案为:C。
根据比例的基本性质:内项积等于外项积,可得8b=3a;将其他选项也根据比例的基本性质写成等式的形式,与8b=3a一致的就说明正确。
38.B
解:3.14×(4÷2)2=12.56(cm2)
12-6=6(cm)
12.56×6+12.56×6×
=75.36+25.12
=100.48(cm3)
故答案为:B。
看图可知火箭模型是由一个圆柱和一个圆锥组合而成的。圆柱的体积=π(d÷2)2h,圆锥的体积=π(d÷2)2h,火箭的体积=圆柱的体积+圆锥的体积。
39.D
解:50m=5000cm,20m=2000cm,
A:5000×=5(厘米),2000×=2(厘米),5×2=10(平方厘米),
B:5000×=(厘米),2000×=(厘米),×≈4(平方厘米),
C:5000×=10(厘米),2000×=4(厘米),10×4=40(平方厘米),
D:5000×=50(厘米),2000×=20(厘米),50×20=1000(平方厘米),
1000最大,所以选用比例尺1:100画出来的平面图面积最大。
故答案为:D。
也可以这样理解,图上距离=实际距离×比例尺,实际距离是固定不变的,所以比例尺越大,图上距离就越大,画出来的平面图形面积就越大;1:100 的比例尺最大,选用比例尺1:100画出来的平面图面积最大。
40.B
解:6-3=3,设甲、乙两个图形的底面半径是r
甲的体积=×3×πr2=πr2
乙的体积=3πr2
(πr2):(3πr2)
=(πr2×):(3πr2×)
=1:3
故答案为:B。
看图可知旋转后的图形:甲图形形成的是一个圆锥,乙图形形成的是一个圆柱;圆锥的高等于组合体高6减去圆柱的高3,通过计算发现它们高相等;再通过观察发现圆锥与圆柱的底面半径都是乙图形的宽,即甲图形的底,所以圆锥的底面积等于圆柱的底面积。综上所述旋转后形成的圆锥与圆柱高和底面积相等,所以圆柱的体积是圆锥体积的3倍,因此体积比=1:3。
41.B
解:3.14×4×8
=12.56×8
=100.48(平方厘米)
故答案为:B。
圆柱的侧面积=底面周长×高=πdh。
42.C
解:博物馆的建筑设计有很多圆柱形的柱子支撑屋顶,工程翻新时打算给这些柱子刷油漆,刷油漆的面积指的是这些柱子的侧面积。
故答案为:C。
根据题意和生活经验分析可知柱子的上面和下面都是无法刷油漆的,所以刷油漆的地方只能是柱子的侧面,即刷油漆的面积指的是这些柱子的侧面积。
43.A
解:A、已走的路程+剩下的路程=学校到家的路程,不成比例;
B、每个人分到的蛋糕大小×人数=蛋糕分成的总块数(一定),即积一定,所以每个人分到的蛋糕大小与人数成反比例关系;
C、长×宽=长方形的面积(一定),即积一定,所以它的长和宽成反比例关系;
D、速度×时间=路程百米(一定),即积一定,所以跑步的速度和时间成反比例关系。
故答案为:A。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用 yx=k(k一定,k不等于0)来表示。
44.B
解:3.14×22=12.56(平方厘米)
3.14×2×2×4
=12.56×4
=50.24(平方厘米)
50.24+12.56×2
=50.24+25.12
=75.36(平方厘米)
故答案为:B。
观察图形可知旋转后得到的是一个高为4厘米,底面半径是2厘米的圆柱。圆柱的底面积=πr2,圆柱的侧面积=2πrh,圆柱的表面积=侧面积+底面积×2。
45.C
解:原体积=πr2h
现在的体积=π(r×)2(2h)
=(×2)πr2h
=πr2h
即体积缩小到原来的。
故答案为:C。
圆柱的体积=πr2h,据此根据题意计算即可得出结论。
46.A
:27米=2700厘米,15米=1500厘米
2700×=9(厘米)
1500×=5(厘米)
故答案为:A。
先根据1米=100厘米,大单位转化成小单位乘进率,将实际距离单位统一成厘米,再根据实际距离×比例尺=图上距离,计算出长和宽的图上距离。
47.B
解:300千米=30000000厘米
6:30000000
=(6÷6):(30000000÷6)
=1:5000000
故答案为:B。
图上距离:实际距离=比例尺,在计算过程中注意将单位统一成厘米。
48.B
解:A、体积÷高=底面积×(一定),即商一定,所以高和体积成正比例关系;
B、用去部分+剩下部分=这根铁丝的长度,所以用去部分和剩下部分不成比例;
C、总价÷数量=单价(一定),即商一定,所以总价和数量成正比例关系;
D、路程÷时间=速度(一定),即商一定,所以路程和时间成正比例关系。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示。
49.D
解:A、1.2:1.3=1.2÷1.3=,4:5=4÷5=,,所以1.2:1.3和4:5不能组成比例;
B、:5=÷5=,:4=÷4=,,所以:5和:4不能组成比例;
C、:4=÷4=,3:12=3÷12=,,所以:4和3:12不能组成比例;
D、1.5:1.2=1.5÷1.2=,5:4=5÷4=,=,所以1.5:1.2和5:4能组成比例。
故答案为:D。
比例:表示两个比相等的式子叫做比例。根据比例的意义可知能否组成比例的判断方法:看两个比的比值是否相等,即如果比值相等它们可以组成比例,如果比值不相等则不能组成比例,据此可以解答。
50.B
解:20m=2000cm,所以数值比例尺是1:2000。
故答案为:B。
图上距离:实际距离=比例尺,线段比例尺是用图上1厘米长的线段表示实际的距离,所以只需要把实际距离的单位转化成厘米即可。
期中考试真题分类汇编04单项选择
一、单选题
1.(2024六下·龙岗期中)丽丽做了一个底面直径是9厘米,高是15厘米的圆柱形的笔筒,她把笔筒高度的以下部分涂上颜色(底面不涂),涂颜色部分的面积是( ) 平方厘米。
A.282.6 B.254.34 C.169.56 D.423.9
2.(2024六下·龙岗期中)雪糕厂制作了底面积相同的三种模具(如下图),倒入同一种雪糕原浆,三种模具装的原浆相比较,( )。
A.正方体多 B.长方体多 C.圆柱多 D.一样多
3.(2024六下·龙岗期中)如下图,一个长方形的长为a,宽为b,分别以长,宽为轴旋转一周,产生了甲、乙两个圆柱。判断甲,乙两个圆柱侧面积的大小关系,( )。
A.甲>乙 B.甲<乙 C.甲=乙 D.无法比较
4.(2024六下·龙岗期中)一个圆柱的高是2dm,沿底面直径切开,横截面是一个正方形,下面说法错误的是( )。
A.这个圆柱的底面半径是1dm
B.这个圆柱的底面面积是3.14 dm2
C.这个圆柱的体积是6.28 dm3
D.这个圆柱切开后表面积增加4 dm2
5.(2024六下·龙岗期中)将一个电话号码牌绕点O逆时针旋转180°后如下图所示,这个电话号码是( )。
A.9916089 B.6616089 C.6619089 D.6806199
6.(2024六下·龙岗期中)把一根圆柱形木料削成一个最大的圆锥,削去部分体积是圆锥的( )。
A.2倍 B. C. D.
7.(2024六下·龙岗期中)如果x和y (x、y均不为0)是两种相关联的量,那么下面表示x和y成正比例关系的是( )。
A.x-y B.y+x C. D.
8.(2024六下·龙岗期中)与线段比例尺大小相同的比例尺是( )。
A.1:2000000 B.1:20 C.1:4000000 D.20:1
9.(2024六下·龙岗期中)在出勤率、出勤人数、全班人数这三个量中,当( )一定时, 另外两个量成反比例。
A.全班人数 B.出勤人数 C.出勤率 D.以上都可以
10.(2024六下·龙岗期中)在下面各比中,与能组成比例的是( )。
A.5 :2 B.2:5 C.:2 D.2:
11.(2024六下·龙岗期中)在下图中,以直线为轴旋转一周,可以得到圆锥的是( )。
A. B. C. D.
12.(2024六下·湛江期中)下列关系中,能表示a和b成反比例的是( )(a、b均不为0)。
A.a+b=5 B.a-b=5 C.= 5 D. =
13.(2024六下·湛江期中)圆柱的底面半径扩大3倍,高不变,它的体积扩大( )。
A.3倍 B.6倍 C.9倍 D.不变
14.(2024六下·湛江期中) 一幅地图的比例尺是1 : 5000000,地图上的1厘米表示实际距离( )。
A.50千米 B.500千米 C.5000千米 D.5000000千米
15.(2024六下·洞头期中)比例尺是1:5000000表示地图上1cm距离相当于实际距离( )
A.50m B.50km C.5km
16.(2024六下·洞头期中)一个圆柱的侧面展开图是一个正方形,这个圆柱的高是底面直径的( ) 倍。
A.π B.2π C. D.
17.(2024六下·洞头期中)平行四边形的高一定,它的面积和底( )
A.成正比例 B.成反比例 C.不成比例
18.(2024六下·洞头期中)某种饼干包装袋上显示“净含量: 95±3g",说明这袋饼干的质量是( )
A.92g B.98g C.92~98g
19.(2024六下·洞头期中)能与组成比例的是( )
A.4:3 B.3:4 C.
20.(2024六下·洞头期中)下面( )图形是圆柱的展开图。(单位:cm)
A.
B.
C.
21.(2024六下·罗湖期中)市政府要建一个长600m,宽400m的长方形广场,将广场设计图画在一张长20cm、宽16cm的长方形纸上,选用下列比例尺( )比较合适。
A.1:2500 B.1:3000 C.1:4000 D.1:4000000
22.(2024六下·罗湖期中)若6y=x(x、y不为0),则x与y( )。
A.成正比例 B.成反比例 C.不成比例 D.无关
23.(2024六下·罗湖期中)用四个同样大小的圆柱拼成一个高为40厘米的大圆柱时,表面积减少了72平方厘米,原来每个小圆柱的体积是( )立方厘米。
A.120 B.240 C.360 D.480
24.(2024六下·罗湖期中)如果正方体、圆柱、圆锥的底面积相等,高也相等。下面说法正确的是( )。
A.正方体的体积最大 B.圆柱的体积是圆锥的
C.圆锥的体积是正方体的 D.圆柱和正方体的表面积相同
25.(2024六下·罗湖期中)能通过下图的箭头旋转得到的是( )。
A. B. C. D.
26.(2024六下·罗湖期中)下图4个圆柱中,与圆锥的体积相等的是( )。
A.A B.B C.C D.D
27.(2024六下·罗湖期中)已知a÷=b×0.4,那么a:b=( )。
A.3:5 B.5:3 C.4:15 D.15:4
28.(2024六下·期中)把圆锥切一刀,切面不可能是( )。
A.三角形 B.椭圆形 C.平行四边形
29.(2024六下·期中)把高是15cm圆锥形容器盛满水,将水倒入等底等高的圆柱形容器,水面高是( )cm。
A.15 B.30 C.5
30.(2024六下·期中) 一幅地图的比例尺是20:1,如果零件图上长5厘米,则实际长( )。
A.4厘米 B.100厘米 C.0.25厘米
31.(2024六下·期中)如下图,柱形瓶底的面积与锥形瓶口的面积相等,将柱形瓶中的饮料倒入锥形瓶中,可以倒满( )杯。
A.2 B.3 C.6
32.(2024六下·盐都期中) 有两支蜡烛,当第一支燃去,第二支燃去时,剩下的部分一样长,第一支 蜡烛与第二支蜡烛原来长度的比是( )
A.6:5 B.5:3 C.2:1 D.3:5
33.(2024六下·盐都期中)体育活动室里,有 10 张乒乓球桌同时进行乒乓球比赛,双打的比单打的多 4 人, 进行双打比赛的乒乓球桌有( )张。
A.6 B.5 C.4 D.3
34.(2024六下·盐都期中)一个圆柱和一个圆锥的体积之比是 3︰4,底面积之比是 4︰3,高的比是 ( )。
A.3︰16 B.1︰3 C.9︰16 D.16︰9
35.(2024六下·盐都期中) 一个圆柱体和一个正方体底面周长和高分别相等,那么圆柱体的体积和正方 体的体积比较( )。
A.正方体大 B.圆柱体大 C.一样大 D.无法比较
36.(2024六下·盐都期中)把一张长方形照片按 1:10 的比例缩小,长与宽的比是( )。
A.不变 B.变了 C.10:1 D.1:10
37.(2024六下·盐都期中)根据 a:8=b:3 写出的比例,正确的是( )
A.a:b=3:8 B.8:a=b:3 C.3:8=b:a D.a:3=b:8
38.(2024六下·龙岗期中)一年一度的科技节正如火如荼的进行中,如图是乐乐参加比赛制作的火箭模型,其体积是( )
A.125.6cm3 B.100.48cm3 C.150.72cm3 D.200.96cm3
39.(2024六下·龙岗期中)为了推进体育强国建设,增强青少年体质,深圳市某小学新建一个长50m,宽20m的恒温游泳池,选用比例尺( )画出来的平面图面积最大。
A.1:1000 B.1:1500 C.1:500 D.1:100
40.(2024六下·龙岗期中)如图,沿直线MN旋转一周后,甲、乙两部分所形成的立体图形的体积比是( )
A.1:2 B.1:3 C.1:6 D.1:9
41.(2024六下·龙岗期中)端午节时,乐乐做了一个底面直径为4cm,高为8cm的圆柱形粽子,现在她要在粽子的侧面沾上一层糖,粽子沾糖的面积是( )cm2。
A.200.96 B.100.48 C.401.92 D.125.6
42.(2024六下·龙岗期中)博物馆的建筑设计有很多圆柱形的柱子支撑屋顶,工程翻新时打算给这些柱子刷油漆,刷油漆的面积指的是这些柱子的( )
A.表面积 B.体积 C.侧面积 D.底面积
43.(2024六下·龙岗期中)下列选项中,两个量不成反比例的是( )
A.乐乐放学回家,已走的路程和剩下的路程。
B.等分一块蛋糕,每个人分到的蛋糕大小与人数。
C.长方形的面积一定,它的长和宽。
D.百米赛跑,跑步的速度和时间。
44.(2024六下·龙岗期中)如图的图形绕虚线旋转一周得到的图形的表面积是( )cm2。
A.50.24 B.75.36 C.12.56 D.100.48
45.(2024六下·龙岗期中)如果一个圆柱的底面半径缩小到原来的,高扩大到原来的2倍,那么体积( )
A.缩小到原来的。 B.扩大到原来的2倍。
C.缩小到原来的。 D.没有变化。
46.(2024六下·龙岗期中)学校小操场内部要进行美化,现收集学生的作品。长方形操场的长和宽是27m和15m,按1:300的比缩小,则缩小后的长和宽是( )
A.9cm和5cm B.9m和5m
C.90cm和50cm D.8100cm和4500cm
47.(2024六下·龙岗期中)2023年2月3日,我国首条设计时速为每小时350千米的跨海高铁——福厦高铁进入静态验收阶段,全长300千米,笑笑画了6cm的路线图,请问笑笑用的比例尺是( )
A.1:7000000 B.1:5000000 C.1:50 D.5000000:1
48.(2024六下·龙岗期中)下列选项中,两个量不成正比例的是( )
A.圆锥的底面积一定,高和体积。
B.一根铁丝,用去部分和剩下部分。
C.单价一定,总价和数量。
D.速度不变,路程和时间。
49.(2024六下·龙岗期中)下面( )组的两个比可以组成比例。
A.1.2:1.3和4:5 B.:5和:4
C.:4和3:12 D.1.5:1.2和5:4
50.(2024六下·龙岗期中)2024年粤港澳大湾区深圳花展在仙湖植物园如期举行,本次花展使用的宣传海报的比例尺是,改写成数值比例尺是( )
A.1:8000 B.1:2000 C.2000:1 D.1:20
答案解析部分
1.C
解:9×3.14×15×
=28.26×6
=169.56(平方厘米)。
故答案为:C。
涂颜色部分的面积=侧面积×涂色部分的高度,其中,侧面积=π×直径×高。
2.D
解:三个立体图形的体积都是:底面积×高,则体积相等。
故答案为:D。
圆柱的体积=长方体的体积=正方体的体积=底面积×高,因为底面积、高都相等, 则体积也相等。
3.C
解:甲:2×π×b×a=2πab;
乙:2×π×a×b=2πab;
甲=乙。
故答案为:C。
圆柱的侧面积=2π×半径×高,然后比较大小。
4.D
解:A项:2÷2=1(分米),原题干说法正确;
B项:3.14×12=3.14(平方分米),原题干说法正确;
C项:3.14×12×2=6.28(立方分米),原题干说法正确;
D项:2×2×2=8(平方分米),原题干说法错误。
故答案为:D。
A项:这个圆柱的底面半径=直径÷2,其中,直径=圆柱的高;
B项:这个圆柱的底面积=π×半径2,
C项:这个圆柱的体积=底面积×高;
D项:这个圆柱切开后增加的表面积=底面直径×高×2。
5.C
解:这个电话号码变成了。
故答案为:C。
将这个个电话号码牌绕点O逆时针旋转180°如图所示,这个电话号码变成6619089。
6.A
解:(1-)÷
=÷
=2。
故答案为:A。
把一根圆柱形木料削成一个最大的圆锥,圆锥的体积是圆柱的,削去部分体积是圆锥体积的分率=(1-圆锥的体积)÷圆锥的体积。
7.C
解:A项:x和y不成比例;
B项:x和y不成比例;
C项:=(一定),x和y成正比例;
D项:xy=(一定),x和y反正比例。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
8.A
解:1:(20×100000)=1:2000000。
故答案为:A。
先单位换算20千米=2000000厘米,比例尺=图上距离÷实际距离。
9.B
解:全班人数×出勤率=出勤人数(一定),当出勤人数一定时, 另外两个量成反比例。
故答案为:B。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
10.A
解:×2=1,×5=1,所以:=5:2。
故答案为:A。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此判断。
11.C
解:直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
故答案为:C。
直角三角形的有两条直角边,依据圆锥的特点,直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
12.D
解:由 =可以化为a×b=3×5,即:a×b=15,a和b成反比例关系。
故答案为:D。
反比例的判断方法:相关联,能变化,积一定。
13.C
解:底面半径扩大3倍,底面积扩大9倍;
底面积扩大9倍,高不变,它的体积扩大9倍。
故答案为:C。
圆的半径、直径、周长扩大的倍数相等,面积扩大的倍数是他们的平方倍;如果高不变,圆锥体积扩大的倍数也是他们的平方倍。
14.A
解:5000000厘米=50000米=50千米,
地图上的1厘米表示实际距离50千米。
故答案为:A。
厘米去掉2个0化为米,米去掉3个0化为千米,据此解答。
15.B
解:1÷÷100000
=5000000÷100000
=50(千米)。
故答案为:B。
实际距离=图上距离÷比例尺,然后单位换算。
16.A
解:底面周长=π×直径,底面周长÷直径=π。
故答案为:A。
一个圆柱的侧面展开图是一个正方形,这个圆柱的高等于底面周长,高是底面直径的π倍。
17.A
解:平行四边形的面积÷底=高(一定),平行四边形的高一定,它的面积和底成正比例。
故答案为:A。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
18.C
解:95-3=92(克),95+3=98(克),说明这袋饼干的质量是92~98克。
故答案为:C。
净含量: 95±3g表示最少的质量=95-3=92克,最多的质量=95+3=98克。
19.A
解:×3=1,×4=1,则可以组成比例:4=:3。
故答案为:A。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此判断。
20.A
解:A、3.14×3=9.42(cm),底面周长与长方形的长相等,是圆柱的展开图;
B、3.14×3=9.42(cm),底面周长与长方形的长不相等,不是圆柱的展开图;
C、底面周长与长方形的长不相等,不是圆柱的展开图。
故答案为:A。
圆柱的侧面积沿着一条高展开后是一个长方形,长方形的长与圆柱的底面周长相等,计算出底面周长再与长方形的长比较后即可判断。
21.C
解:600m=60000cm,400m=40000cm
选项A:长:60000×=24(cm),宽:40000×=160(cm),24>20,16=16,不合适;
选项B:长:60000×=20(cm),宽:40000×=(cm),20=20,<16,但是不是整数,不合适;
选项C:长:60000×=15(cm),宽:40000×=10(cm),15<20,10<16,合适;
选项D:长:60000×=0.015(cm),宽:40000×=0.01(cm),0.015与0.01过于小,不合适;
故答案为:C。
根据图上距离=实际距离×比例尺,分别计算出按照各个比例尺画的图上长度,选择合适的即可。
22.A
解:若6y=x,则x÷y=6(一定),比值一定,x和y成正比例。
故答案为:A。
两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,则这两种量成正比例关系;如果这两种量的乘积一定,则这两种量成反比例关系。
23.A
解:72÷6×(40÷4)
=12×10
=120(立方厘米);
故答案为:A。
减少的表面积是6个底面积,因此,用减少的表面积除以6求出底面积,再根据圆柱体积=底面积×高,代入数值计算即可。
24.C
解:圆柱的体积=正方体的体积,圆锥的体积=圆柱的体积=正方体的体积;
故答案为:C。
正方体与圆柱的体积都是底面积乘高,因此,等底等高的情况下,圆柱与正方体的体积相等;圆锥的体积是与它等底等高的圆柱体积的;据此解答。
25.D
解:将该图形顺时针旋转90°、180°、270°,得到的图形依次是:、、;
故答案为:D。
将已知图形顺时针旋转90°、180°、270°,得到的图形与各个选项比较即可。
26.C
解:选项A:该圆柱与圆锥等底等高,所以它的体积是圆锥体积的3倍;
选项B:该圆柱与圆锥等高,底面积是圆锥的,所以它的体积是圆锥体积的;
选项C:该圆柱与圆锥等底,高是圆锥的,所以它的体积与圆锥的体积相等;
选项D:该圆锥的高是圆锥的,底面积是圆锥的,所以它的体积是圆锥体积的;
故答案为:C。
等底等高的圆柱体积是圆锥体积的3倍,因此,圆柱与圆锥的体积和高相等时,圆锥的底面积是圆柱的3倍;当圆柱与圆锥的体积和底面积相等时,圆锥的高是圆柱的3倍;据此解答。
27.C
解:a÷=a×,即a×=b×0.4,所以a:b=0.4:=4:15;
故答案为:C。
根据比例的基本性质:内项积等于外项,将其改写成比例的形式,再化简比即可。
28.C
解:把圆锥沿着顶点到底面直径切一刀,切面是三角形,沿着圆锥的一侧切一刀,切面是椭圆形,不可能是平行四边形。
故答案为:C。
圆锥有一个圆形的底面和一个曲面,把圆锥切一刀,切面不可能是平行四边形。
29.C
解:15÷3=5(厘米)。
故答案为:C。
等底等高的圆柱的体积是圆锥体积的3倍,圆柱形容器水面的高度=圆锥的高÷3。
30.C
解:5÷20=0.25(厘米)。
故答案为:C。
实际距离=图上距离÷比例尺。
31.C
解:3×2=6(杯)。
故答案为:C。
等底等高的圆柱的体积是圆锥体积的3倍,圆柱的高是圆锥高的2倍,底面积相等,则将柱形瓶中的饮料倒入锥形瓶中,可以倒满6杯。
32.B
解:第一支原来的长度×(1-)=第二支原来的长度×(1-),所以第一支原来的长度:第二支原来的长度=(1-):(1-)=:=5:3;
故答案为:B。
由题意可知,第一支剩下的长度=第一支原来的长度×(1-),第二支剩下的长度=第二支原来的长度×(1-),两支剩下的部分一样长,即第一支原来的长度×(1-)=第二支原来的长度×(1-),再根据比的基本性质:内项积等于外项积,即可求出第一支蜡烛与第二支蜡烛原来长度的比。
33.C
解:设进行双打比赛的乒乓球桌有x张,则进行单打比赛的乒乓球桌有(10-x)张。
4x-2×(10-x)=4
4x-20+2x=4
6x=24
x=4
故答案为:4。
可以设进行双打比赛的乒乓球桌有x张,则进行单打比赛的乒乓球桌有(10-x)张,题中的等量关系是:双打总人数-单打总人数=4,据此列方程解答。
34.A
解:假设圆柱和圆锥的体积分别是3和4,底面积分别是4和3;
圆柱的高:3÷4=;
圆锥的高:4×3÷3=4;
高的比是::4=3:16;
故答案为:A。
假设圆柱和圆锥的体积分别是3和4,底面积分别是4和3;根据圆柱的高=体积÷底面积,圆锥的高=体积×3÷底面积,分别求出圆柱和圆锥的高,再求出高的比。
35.B
解:周长相等的情况下,圆的面积大于正方形面积,即圆柱的底面积>正方形底面积,又因为它们的高相等,所以圆柱的底面积×高>正方形的底面积×高,圆柱的体积>正方体的体积。
故答案为:B。
周长相等的情况下,圆的面积大于正方形面积,根据圆柱体积=底面积×高,正方形体积=底面积×高,即可比较两个体积的大小。
36.A
解:原来长与宽的比是:长:宽;
缩小后的长与宽的比是:长:宽=长:宽;
因此,长与宽的比不变;
故答案为:A。
按照1:10的比例缩小,即长方形缩小后的长为原来长的,长方形缩小后的宽为原来宽的,据此解答。
37.C
解:根据a:8=b:3,可得:8b=3a;
选项A:根据a:b=3:8,可得3b=8a,不符合8b=3a,错误;
选项B:根据8:a=b:3,可得ab=8×3,不符合8b=3a,错误;
选项C:根据3:8=b:a,可得8b=3a,符合8b=3a,正确;
选项D:根据a:3=b:8,可得3b=8a,不符合8b=3a,错误;
故答案为:C。
根据比例的基本性质:内项积等于外项积,可得8b=3a;将其他选项也根据比例的基本性质写成等式的形式,与8b=3a一致的就说明正确。
38.B
解:3.14×(4÷2)2=12.56(cm2)
12-6=6(cm)
12.56×6+12.56×6×
=75.36+25.12
=100.48(cm3)
故答案为:B。
看图可知火箭模型是由一个圆柱和一个圆锥组合而成的。圆柱的体积=π(d÷2)2h,圆锥的体积=π(d÷2)2h,火箭的体积=圆柱的体积+圆锥的体积。
39.D
解:50m=5000cm,20m=2000cm,
A:5000×=5(厘米),2000×=2(厘米),5×2=10(平方厘米),
B:5000×=(厘米),2000×=(厘米),×≈4(平方厘米),
C:5000×=10(厘米),2000×=4(厘米),10×4=40(平方厘米),
D:5000×=50(厘米),2000×=20(厘米),50×20=1000(平方厘米),
1000最大,所以选用比例尺1:100画出来的平面图面积最大。
故答案为:D。
也可以这样理解,图上距离=实际距离×比例尺,实际距离是固定不变的,所以比例尺越大,图上距离就越大,画出来的平面图形面积就越大;1:100 的比例尺最大,选用比例尺1:100画出来的平面图面积最大。
40.B
解:6-3=3,设甲、乙两个图形的底面半径是r
甲的体积=×3×πr2=πr2
乙的体积=3πr2
(πr2):(3πr2)
=(πr2×):(3πr2×)
=1:3
故答案为:B。
看图可知旋转后的图形:甲图形形成的是一个圆锥,乙图形形成的是一个圆柱;圆锥的高等于组合体高6减去圆柱的高3,通过计算发现它们高相等;再通过观察发现圆锥与圆柱的底面半径都是乙图形的宽,即甲图形的底,所以圆锥的底面积等于圆柱的底面积。综上所述旋转后形成的圆锥与圆柱高和底面积相等,所以圆柱的体积是圆锥体积的3倍,因此体积比=1:3。
41.B
解:3.14×4×8
=12.56×8
=100.48(平方厘米)
故答案为:B。
圆柱的侧面积=底面周长×高=πdh。
42.C
解:博物馆的建筑设计有很多圆柱形的柱子支撑屋顶,工程翻新时打算给这些柱子刷油漆,刷油漆的面积指的是这些柱子的侧面积。
故答案为:C。
根据题意和生活经验分析可知柱子的上面和下面都是无法刷油漆的,所以刷油漆的地方只能是柱子的侧面,即刷油漆的面积指的是这些柱子的侧面积。
43.A
解:A、已走的路程+剩下的路程=学校到家的路程,不成比例;
B、每个人分到的蛋糕大小×人数=蛋糕分成的总块数(一定),即积一定,所以每个人分到的蛋糕大小与人数成反比例关系;
C、长×宽=长方形的面积(一定),即积一定,所以它的长和宽成反比例关系;
D、速度×时间=路程百米(一定),即积一定,所以跑步的速度和时间成反比例关系。
故答案为:A。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用 yx=k(k一定,k不等于0)来表示。
44.B
解:3.14×22=12.56(平方厘米)
3.14×2×2×4
=12.56×4
=50.24(平方厘米)
50.24+12.56×2
=50.24+25.12
=75.36(平方厘米)
故答案为:B。
观察图形可知旋转后得到的是一个高为4厘米,底面半径是2厘米的圆柱。圆柱的底面积=πr2,圆柱的侧面积=2πrh,圆柱的表面积=侧面积+底面积×2。
45.C
解:原体积=πr2h
现在的体积=π(r×)2(2h)
=(×2)πr2h
=πr2h
即体积缩小到原来的。
故答案为:C。
圆柱的体积=πr2h,据此根据题意计算即可得出结论。
46.A
:27米=2700厘米,15米=1500厘米
2700×=9(厘米)
1500×=5(厘米)
故答案为:A。
先根据1米=100厘米,大单位转化成小单位乘进率,将实际距离单位统一成厘米,再根据实际距离×比例尺=图上距离,计算出长和宽的图上距离。
47.B
解:300千米=30000000厘米
6:30000000
=(6÷6):(30000000÷6)
=1:5000000
故答案为:B。
图上距离:实际距离=比例尺,在计算过程中注意将单位统一成厘米。
48.B
解:A、体积÷高=底面积×(一定),即商一定,所以高和体积成正比例关系;
B、用去部分+剩下部分=这根铁丝的长度,所以用去部分和剩下部分不成比例;
C、总价÷数量=单价(一定),即商一定,所以总价和数量成正比例关系;
D、路程÷时间=速度(一定),即商一定,所以路程和时间成正比例关系。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示。
49.D
解:A、1.2:1.3=1.2÷1.3=,4:5=4÷5=,,所以1.2:1.3和4:5不能组成比例;
B、:5=÷5=,:4=÷4=,,所以:5和:4不能组成比例;
C、:4=÷4=,3:12=3÷12=,,所以:4和3:12不能组成比例;
D、1.5:1.2=1.5÷1.2=,5:4=5÷4=,=,所以1.5:1.2和5:4能组成比例。
故答案为:D。
比例:表示两个比相等的式子叫做比例。根据比例的意义可知能否组成比例的判断方法:看两个比的比值是否相等,即如果比值相等它们可以组成比例,如果比值不相等则不能组成比例,据此可以解答。
50.B
解:20m=2000cm,所以数值比例尺是1:2000。
故答案为:B。
图上距离:实际距离=比例尺,线段比例尺是用图上1厘米长的线段表示实际的距离,所以只需要把实际距离的单位转化成厘米即可。
同课章节目录
