期中考试真题分类汇编13填空题(含答案+解析)---2024-2025学年北师大版六年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编13填空题(含答案+解析)---2024-2025学年北师大版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 107.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 08:18:59 | ||
图片预览




文档简介
2024-2025学年北师大版六年级数学下册
期中考试真题分类汇编13填空题
一、填空题
1.(2024六下·黄石期中)把2×6=3×4改写成比例,可以是 ,共可以组成 个不同的比例。
2.(2024六下·黄石期中)0.625= %= = (最简比)。
3.(2024六下·陆川期中)一个圆柱的体积是48dm3,与它等底等高的圆锥的体积是 。
4.(2024六下·鹰潭期中)一个圆柱的底面直径和高都是10cm,这个圆柱的侧面积是 。
5.(2024六下·瑞金期中)如下图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了 平方厘米。
6.(2024六下·瑞金期中)西游记中的孙悟空正直勇敢、嫉恶如仇,他有一件神奇的兵器叫如意金箍棒,可以任意缩小或放大。如果孙悟空把如意金箍棒变化成底面周长是6.28分米,长是100分米的圆柱形铁棒,那么此时,它的体积是 立方分米。
7.(2024六下·瑞金期中)妈妈把80000元存入银行,存期为三年定期,年利率1.95%。请提出数学问题: ,列出算式: 。
8.(2024六下·玉田期中)当=(y≠0)时,x和y成 比例。
9.(2024六下·鹰潭期中)写出两个比值都是的比,再组成比例是 。
10.(2024六下·鹰潭期中) 既不是正数,也不是负数,零下3℃记作 。
11.(2024六下·陆川期中)在比例里,两个外项的积等于两个内项的积,这叫作 。
12.(2024六下·南昌期中)8a=12b,那么a:b= : ,a:12= : 。
13.(2024六下·玉田期中)实验小学六⑴班学生的平均体重是39千克,如表所示是该班5名学生的体重统计表
学号 1 2 3 4 5
体重(千克) 35 39 50
与平均体重相比(千克) ﹣4 +5 ﹣7
14.(2024六下·玉田期中)每盒乒乓球的个数一定,乒乓球的总个数和需要的盒数成 比例。
15.(2024六下·玉田期中)在﹣8,0.2,﹣11,+,0,96中,整数有 个。
16.(2024六下·玉田期中)如果前进30米记作+30米,那么后退20米记作 。
17.(2024六下·陆川期中)据我国第一辆火星车“祝融号”反馈的数据显示,火星表面温度白天最高约零上27℃,可以记为℃,晚上最低温度约零下130℃,可以记为 ℃。
18.(2024六下·瑞金期中)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,它的长是 cm,宽是 cm。
19.(2024六下·陆川期中)圆柱的两个底面圆心之间的距离叫作 。
20.(2024六下·陆川期中)根据24×3=8×9,请你写出两个比例 , 。
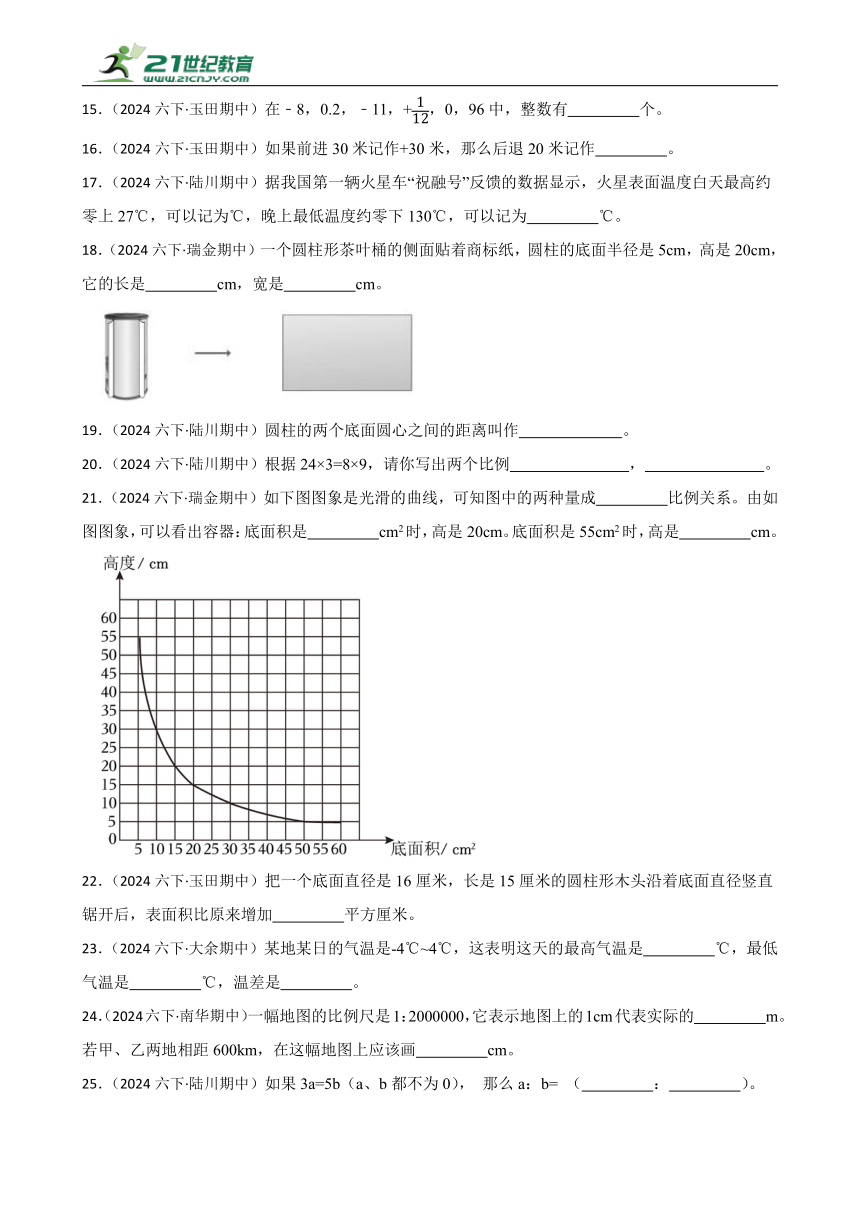
21.(2024六下·瑞金期中)如下图图象是光滑的曲线,可知图中的两种量成 比例关系。由如图图象,可以看出容器:底面积是 cm2时,高是20cm。底面积是55cm2时,高是 cm。
22.(2024六下·玉田期中)把一个底面直径是16厘米,长是15厘米的圆柱形木头沿着底面直径竖直锯开后,表面积比原来增加 平方厘米。
23.(2024六下·大余期中)某地某日的气温是-4℃~4℃,这表明这天的最高气温是 ℃,最低气温是 ℃,温差是 。
24.(2024六下·南华期中)一幅地图的比例尺是1:2000000,它表示地图上的1cm代表实际的 m。若甲、乙两地相距600km,在这幅地图上应该画 cm。
25.(2024六下·陆川期中)如果3a=5b(a、b都不为0), 那么a:b= ( : )。
26.(2024六下·陆川期中)= :2.5= = % (小数) 折= 成。
27.(2024六下·南昌期中)一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是 cm,和它等底等高的圆柱的体积是 cm3。
28.(2024六下·瑞金期中) 一张精密仪器图纸,用5cm长表示实际长5mm,则这幅图的比例尺是 。
29.(2024六下·玉田期中)一个圆锥的体积是10.5cm3,和它等底等高的圆柱的体积是 cm3。
30.(2024六下·陆川期中)在一个比例里,两个内项互为倒数,其中一个外项是3,另一个外项是 .
31.(2024六下·鹰潭期中)把一个圆柱侧面展开,得到一个正方形,这个圆柱的底面直径是8cm,圆柱的高是 。
32.(2024六下·鹰潭期中)15: =0.75=21÷ = 折
33.(2024六下·鹰潭期中)如果a与b互为倒数,并且那么c= ,= 。
34.(2024六下·大余期中)用一张长15cm,宽12cm的长方形纸围成一个圆柱,圆柱的侧面积是 cm2。
35.(2024六下·鹰潭期中)把3×40=20×6,改写成比例是 。
36.(2024六下·大余期中)0.4立方米= 升
1600毫升= 立方分米
10.4平方米= 平方米 平方分米
5时40分= 时
37.(2024六下·鹰潭期中)一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作 千米;+10千米表示 。
38.(2024六下·大余期中)把一根长10dm的圆柱形钢柱截成两段,表面积比原来增加:,这根圆柱原来的体积是 dm3。
39.(2024六下·大余期中)等底等高的圆柱和圆锥体,它们的体积之和是150立方米,圆锥的体积是 立方米。
40.(2024六下·南昌期中)在一幅地图上,20cm的长度表示实际距离18km,这幅地图的比例尺是 ,如果甲,乙两地之间的实际距离4.5km,那么在这幅地图上应该用 cm来表示。
41.(2024六下·南昌期中)一个圆柱体,底面周长是31.4cm,高6cm,它的表面积是 cm2,体积是 cm3。
42.(2024六下·南昌期中)一辆自行车原价350元,打九折后是 元,另一辆自行车打九折后是270元,这辆自行车的原价是 元。
43.(2024六下·鹰潭期中)在中,图中1cm表示实际距离 km,改写成数值比例尺是 。
44.(2024六下·南昌期中)圆柱的底面半径和高都扩大到原来的2倍,则它的底面积扩大到原来的 倍,体积扩大到原来的 倍。
45.(2024六下·大余期中)在比例尺为1:5000000的地图上,南昌、广州两地相距16cm,在另一幅比例尺为1:4000000的地图上,南昌、广州两地相距 厘米。
46.(2024六下·南昌期中)x,y都不为0,,则x和y成 比例,若9m=7n,则m和n成 比例。
47.(2024六下·大余期中)一个直角三角形的两条直角边分别为6cm,10cm,若以6cm的边为轴旋转一周,所围图形的体积是 cm3。
48.(2024六下·鹰潭期中)把一个棱长是6cm的正方体削成一个最大的圆锥体,这个圆锥的体积是 。
49.(2024六下·大余期中)0.6:3= :18= = %
50.(2024六下·大余期中)天虹超市举行“五一”商品大推销,有一套“”玩具打九折出售,“九折”表示现价相当于原价的 %,如果这件玩具现价卖72元,那么原价是 。
答案解析部分
1.6:3=4:2,3:6=2:4,2:3=4:6,3:2=6:4;4
解:可以改成的比例有:6:3=4:2,3:6=2:4,2:3=4:6,3:2=6:4,
共可以组成4个不同的比例。
故答案为:6:3=4:2,3:6=2:4,2:3=4:6,3:2=6:4;4。
两个比只要比值相等,就可以组成比例,据此解答。
2.62.5;5;5:8
解:0.625==62.5%==5:8。
故答案为:62.5;5;5:8。
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;
小数化分数:小数点后有几位小数,就在1后面添几个0做分母,小数点去掉做分子。能约分的要约成最简分数;分数可以写成比的形式,分子是比的前项,分母是比的后项。
3.16立方分米
解:48÷3=16(立方分米)。
故答案为:16立方分米。
与圆柱等底等高的圆锥的体积=圆柱的体积÷3。
4.314cm2
解:3.14×10×10=314(cm2)
故答案为:314cm2。
圆柱的侧面积=底面周长×高,根据公式计算圆柱的侧面积即可。
5.64
解:8×4×2
=32×2
=64(cm2)
故答案为:64。
圆柱切开后的一个切面是一个长方形,增加的面积就是2个长是8cm,宽是4cm的长方形的面积。
6.314
解:6.28÷3.14÷2=1(分米)
3.14×1×100
=3.14×100
=314(立方分米)
故答案为:314。
孙悟空的如意金箍棒如果是圆柱形,圆柱的体积 = π × (底面半径的平方) × 高;据此代入数值计算。
7.妈妈能获得利息多少元;80000×3×1.95%
解:问题:妈妈能获得利息多少元?
本金是80000元,年利率是1.95%,存款时间为三年,所以利息为:80000×3×1.95%(元)。
故答案为:妈妈能获得利息多少元; 80000×3×1.95%。
利息=本金×利率×存款时间;据此提出问题列出算式。
8.反
解:由=可得:xy=8×5=40, x和y成反比例。
故答案为:反。
比例的基本性质:比例的外项之积等于比例的内项之积;
反比例的判断方法:相关联,能变化,积一定。
9.1:2=2:4
解:写出两个比值都是的比,再组成比例是1:2=2:4。
故答案为:1:2=2:4(答案不唯一)。
比例是表示两个比相等的式子。由此写出两个比值是的比,再组成比例即可。
10.0;-3℃
解:0既不是正数,也不是负数,零下3℃记作-3℃。
故答案为:0;-3℃。
正负数表示相反意义的量,高于0℃的温度记作正,低于0℃的温度就记作负。
11.比例的基本性质
解:在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
故答案为:比例的基本性质。
比例的基本性质:在比例里,两个内项积等于两个外项积。
12.3;2;b;8
解:a:b=12:8=3:2;a:12=b:8。
故答案为:3;2;b;8。
比例的基本性质:在一个比例中,两个外项的积等于两个内项的积。如果a是外项,b是内项,则8为外项,12为内项,在化简比。如果a是外项,12是内项,则8为外项,b为内项。
13.44;32;0;+11
解:第一空:39+5=44(千克)
第二空:39-7=32(千克)
第三空:39-39=0(千克)
第四空:50-39=11(千克)
学号 1 2 3 4 5
体重(千克) 35 44 39 50 32
与平均体重相比(千克) ﹣4 +5 0 +11 ﹣7
故答案为:44;32;0;+11。
比39千克多的质量用正数表示,比39千克少的质量用负数表示,正数表示比39千克多的质量,负数表示比39千克少的质量,据此解答。
14.正
解:乒乓球的总个数÷需要的盒数=每盒乒乓球的个数(一定),
乒乓球的总个数和需要的盒数成正比例。
故答案为:正。
正比例的判断方法:相关联,能变化,商一定。
15.4
解:﹣8,﹣11,0,96都是整数,有4个。
故答案为:4。
整数包括正整数、0、负整数。
16.﹣20米
解:如果前进30米记作+30米,那么后退20米记作-20米。
故答案为:-20米。
前进用正数表示,后退就用负数表示。
17.-130
解:零上27℃,可以记为+27℃,零下130℃,可以记为-130℃。
故答案为:-130。
零上温度用正数表示,零下温度用负数表示。
18.31.4;20
解:2×π×5
=2×3.14×5
=31.4(cm)
圆柱的高即为商标纸的宽,为20cm。
故答案为:31.4;20。
圆柱的侧面展开后是一个长方形,其长等于圆柱底面的周长,宽等于圆柱的高;圆柱的底面积:S=r2。
19.圆柱的高
解:圆柱的两个底面圆心之间的距离叫作圆柱的高。
故答案为:圆柱的高。
圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条。
20.24:8=9:3;8:3=24:9
解:可以写出比例24:8=9:3或者8:3=24:9(答案不唯一)。
故答案为:24:8=9:3;8:3=24:9。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此写比例。
21.反;15;5
解:反比例图像是一条光滑的曲线;
当高度是20cm,底面积是300÷20=15(cm2);
当底面积是55cm2时,高度是:300÷55≈5(cm)
故答案为:反;15;5。
反比例指的是两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
22.480
解:表面积比原来增加了2个长方形,
16×15×2
=240×2
=480(平方厘米)
表面积比原来增加480平方厘米。
故答案为:480。
底面直径×长=增加的一个面的面积,增加的一个面的面积×2=增加的面积。
23.4;-4;8℃
解:4-(-4℃)=8℃
这天的最高气温是4℃,最低气温是-4℃,温差是8℃。
故答案为:4;-4;8℃。
气温高于0℃记作正,则低于0℃就记作负。用最高气温减去最低气温求出温差。
24.20000;30
比例尺是1:2000000,表示地图上1cm代表实际距离2000000cm,换成m做单位后就是20000m;
600km=60000000cm,60000000×=30(cm)。
故答案为:20000m;30cm。
图上距离:实际距离=比例尺(1:2000000 ) ,就是表示图上1cm代表实际距离2000000cm,但题中的单位是m,所以还要注意化好单位即可;图上距离=实际距离×比例尺(比例尺的分数形式),先将实际距离化成用cm做单位再去求解即可。
25.5;3
解:3a=5b,那么a:b=5:3。
故答案为:5;3。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此解答。
26.1;30;40;0.4;四;四
解:1.6:4=1.6÷4=0.4
2.5×0.4=1;
12÷0.4=30;
0.4=40%=四折=四成;
所以1.6:4=1:2.5==40%=0.4=四折=四成。
故答案为:1;30;40;0.4;四;四。
求比值=比的前项÷比的后项,比的前项=比的后项×比值;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;
百分数与折扣的互化,百分之几十就是几折;百分之几十就等于几成。
27.8;226.08
解:3.14×(6÷2)2=28.26(cm2)
75.36÷÷28.26
=226.08÷28.26
=8(cm)
75.36×3=226.08(cm3)
故答案为:8;226.08。
πr2=圆锥的底面积,圆锥的体积÷÷底面积=圆锥的高;
根据圆柱与圆锥体积的关系可知:等底等高的圆柱的体积是圆锥体积的3倍,据此可以解答。
28.10:1
解:图上距离是5cm,转换为毫米是5cm ×10 = 50mm,
5cm:5mm
=50mm:5mm
=10:1
故答案为:10:1。
比例尺=图上距离:实际距离;先进行单位换算,再求出比例尺。
29.31.5
解:10.5×3=31.5(立方厘米)
和它等底等高的圆柱的体积是31.5立方厘米
故答案为:31.5。
等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
30.
解:在一个比例里,两个内项互为倒数,
可知两个外项也互为倒数,其中一个外项是3,所以另一个外项就是3的倒数 .
故答案为: .
由“在一个比例里,两个内项互为倒数”,根据比例的性质“两外项的积等于两内项的积”,可知两个外项也互为倒数;再根据“其中一个外项是3”,进而求出3的倒数得解.
31.25.12cm
解:3.14×8=25.12(cm)
故答案为:25.12cm。
圆柱的侧面展开是正方形,那么圆柱的高与底面周长相等,所以计算出圆柱的底面周长就是这个圆柱的高。
32.20;28;七五
解:15÷0.75=20,21÷0.75=28,所以15:20=0.75=21÷28=七五折。
故答案为:20;28;七五。
比值和商都是0.75,可以用前项除以比值求出后项,用被除数除以商求出除数;把小数化成百分数再确定折扣。
33.;
解:则ab=5c,ab=1,所以5c=1,则c=;
=×=。
故答案为:;。
根据比例的基本性质把这个比例写成两个內项积等于两个外项积的行驶,a与b互为倒数,则a、b的积是1,这样就能求出c的值,然后求出的值即可。
34.180
解:15×12=180(平方厘米)
故答案为:180。
根据圆柱的侧面展开图的特点:圆柱的底面周长是长方形的长,圆柱的高是长方形的宽,所以这个圆柱的侧面积就是这个长方形的面积;用长乘宽即可。
35.3:20=6:40
解:把3×40=20×6,改写成比例是3:20=6:40。
故答案为:3:20=6:40。(答案不唯一)
在比例里,两个內项的积等于两个外项的积。把3和40作为外项,20和6就是內项,然后写出比例即可。
36.400;1.6;10;40;
解:0.4×1000=400,0.4立方米=400升;
1600÷1000=1.6,1600毫升=1.6立方分米;
0.4×100=40,10.4平方米=10平方米40平方分米;
40÷60=,5时40分=时。
故答案为:400;1.6;10,40;。
1立方米=1000立方分米,1升=1000毫升, 1升=1立方分米, 1平方米=100平方分米,1小时=60分,单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
37.-20;向东行10千米
解:一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作-20千米;+10千米表示向东行10千米。
故答案为:-20;向东行10千米。
以学校为起点,向东走记作正,向西走记作负。根据正负数的意义填空即可。
38.0.18
解:10dm=100cm
3.6÷2×100
=1.8×100
=180(立方厘米)
180立方厘米=0.18立方分米
故答案为:0.18。
把一根长10dm的圆柱形钢柱截成两段 ,增加了2个面,每个面积都是圆柱的底面积,用3.6除以2求出圆柱的底面积,再根据圆柱的体积公式V=Sh,求出圆柱的体积,再换算单位。
39.37.5
解:150÷(3+1)
=150÷4
=37.5(立方米)
故答案为:37.5。
等底等高的圆柱的体积是圆锥体积的3倍,它们的体积之和是(3+1)倍,由此计算圆锥的体积即可。
40.1:90000;5
解:18km=1800000cm,20:1800000=1:900000;
4.5km=450000cm,450000×=5(cm)。
故答案为:1:90000;5。
图上距离:实际距离=比例尺,图上距离=实际距离×比例尺,1km=100000cm。
41.345.4;471
解:半径:31.4÷3.14÷2=5(厘米),表面积:31.4×6+2×3.14×52=345.4(平方厘米);体积:3.14×52×6=471(立方厘米)。
故答案为:345.4;471。
半径=圆的周长÷π÷2;圆柱的表面积=2×底面积+侧面积,其中底面积=π×半径2;侧面积=底面周长×高;圆柱的体积=π×半径2×高。
42.315;300
解:现价:350×90%=315(元);原价:270÷90%=300(元)。
故答案为:315;300。
在折扣问题中,现价与原价的关系为:现价=原价×折扣。
43.40;1:4000000
解:在中,图中1cm表示实际距离40km,改写成数值比例尺是1cm:40km=1cm:4000000cm=1:4000000。
故答案为:40;1:4000000。
线段比例尺表示图上1厘米相当于实际距离40千米。写出图上距离与实际距离的比,统一单位后写成前项是1的比就可以改写成数值比例尺。
44.4;8
解:假设圆柱的底面半径和高都为1,则扩大后都为2,扩大后的底面积为:,扩大后的体积为:。
故答案为:4;8。
圆的面积=π×半径2;圆柱的体积=π×半径2×高。
45.20
解:16÷=80000000(厘米)
80000000×=20(厘米)
故答案为:20。
依据“实际距离=图上距离÷比例尺”即可求出南昌、广州两地的实际距离,再根据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离。
46.反;正
解:xy=8(一定),乘积一定,成反比例关系;m:n=7:9(一定),比值一定,成正比例关系。
故答案为:反;正。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的比值(或商)一定,那么它们的关系称为正比例关系。
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,这两种量就叫做反比例的量。它们的关系称为反比例关系。
47.628
解:3.14×102×6×
=314×6×
=314×2
=628(立方厘米)
故答案为:628。
将这个直角三角形以6厘米为轴旋转一周,可得到一个以6厘米为高、以10厘米为底面半径的圆锥体,根据圆锥的体积公式V=sh进行计算。
48.56.52cm3
解:3.14×(6÷2)2×6×
=3.14×9×2
=56.52(cm3)
故答案为:56.52cm3。
把这个正方体削成最大的圆锥,圆锥的底面直径和高都与正方体的棱长相等。圆锥的体积=底面积×高×,根据公式计算圆锥的体积即可。
49.3.6;90;20
解:0.6×6=3.6
3×30=90
18÷90=0.2=20%
0.6:3=3.6:18==20%
故答案为:3.6;90;20。
根据比的基本性质,0.6:3的前、后项都乘6就是3.6:18;根据比与分数的关系0.6:3=,根据分数的基本性质,分子、分母都乘30就是;18÷90=0.2,0.2改写成百分数是20%。
50.90;80
解: “九折”表示现价相当于原价的90%。
72÷90%=80(元)
故答案为:90;80。
打几折,表示现价是原价的百分之几十;用现价÷折扣=原价。
期中考试真题分类汇编13填空题
一、填空题
1.(2024六下·黄石期中)把2×6=3×4改写成比例,可以是 ,共可以组成 个不同的比例。
2.(2024六下·黄石期中)0.625= %= = (最简比)。
3.(2024六下·陆川期中)一个圆柱的体积是48dm3,与它等底等高的圆锥的体积是 。
4.(2024六下·鹰潭期中)一个圆柱的底面直径和高都是10cm,这个圆柱的侧面积是 。
5.(2024六下·瑞金期中)如下图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了 平方厘米。
6.(2024六下·瑞金期中)西游记中的孙悟空正直勇敢、嫉恶如仇,他有一件神奇的兵器叫如意金箍棒,可以任意缩小或放大。如果孙悟空把如意金箍棒变化成底面周长是6.28分米,长是100分米的圆柱形铁棒,那么此时,它的体积是 立方分米。
7.(2024六下·瑞金期中)妈妈把80000元存入银行,存期为三年定期,年利率1.95%。请提出数学问题: ,列出算式: 。
8.(2024六下·玉田期中)当=(y≠0)时,x和y成 比例。
9.(2024六下·鹰潭期中)写出两个比值都是的比,再组成比例是 。
10.(2024六下·鹰潭期中) 既不是正数,也不是负数,零下3℃记作 。
11.(2024六下·陆川期中)在比例里,两个外项的积等于两个内项的积,这叫作 。
12.(2024六下·南昌期中)8a=12b,那么a:b= : ,a:12= : 。
13.(2024六下·玉田期中)实验小学六⑴班学生的平均体重是39千克,如表所示是该班5名学生的体重统计表
学号 1 2 3 4 5
体重(千克) 35 39 50
与平均体重相比(千克) ﹣4 +5 ﹣7
14.(2024六下·玉田期中)每盒乒乓球的个数一定,乒乓球的总个数和需要的盒数成 比例。
15.(2024六下·玉田期中)在﹣8,0.2,﹣11,+,0,96中,整数有 个。
16.(2024六下·玉田期中)如果前进30米记作+30米,那么后退20米记作 。
17.(2024六下·陆川期中)据我国第一辆火星车“祝融号”反馈的数据显示,火星表面温度白天最高约零上27℃,可以记为℃,晚上最低温度约零下130℃,可以记为 ℃。
18.(2024六下·瑞金期中)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,它的长是 cm,宽是 cm。
19.(2024六下·陆川期中)圆柱的两个底面圆心之间的距离叫作 。
20.(2024六下·陆川期中)根据24×3=8×9,请你写出两个比例 , 。
21.(2024六下·瑞金期中)如下图图象是光滑的曲线,可知图中的两种量成 比例关系。由如图图象,可以看出容器:底面积是 cm2时,高是20cm。底面积是55cm2时,高是 cm。
22.(2024六下·玉田期中)把一个底面直径是16厘米,长是15厘米的圆柱形木头沿着底面直径竖直锯开后,表面积比原来增加 平方厘米。
23.(2024六下·大余期中)某地某日的气温是-4℃~4℃,这表明这天的最高气温是 ℃,最低气温是 ℃,温差是 。
24.(2024六下·南华期中)一幅地图的比例尺是1:2000000,它表示地图上的1cm代表实际的 m。若甲、乙两地相距600km,在这幅地图上应该画 cm。
25.(2024六下·陆川期中)如果3a=5b(a、b都不为0), 那么a:b= ( : )。
26.(2024六下·陆川期中)= :2.5= = % (小数) 折= 成。
27.(2024六下·南昌期中)一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是 cm,和它等底等高的圆柱的体积是 cm3。
28.(2024六下·瑞金期中) 一张精密仪器图纸,用5cm长表示实际长5mm,则这幅图的比例尺是 。
29.(2024六下·玉田期中)一个圆锥的体积是10.5cm3,和它等底等高的圆柱的体积是 cm3。
30.(2024六下·陆川期中)在一个比例里,两个内项互为倒数,其中一个外项是3,另一个外项是 .
31.(2024六下·鹰潭期中)把一个圆柱侧面展开,得到一个正方形,这个圆柱的底面直径是8cm,圆柱的高是 。
32.(2024六下·鹰潭期中)15: =0.75=21÷ = 折
33.(2024六下·鹰潭期中)如果a与b互为倒数,并且那么c= ,= 。
34.(2024六下·大余期中)用一张长15cm,宽12cm的长方形纸围成一个圆柱,圆柱的侧面积是 cm2。
35.(2024六下·鹰潭期中)把3×40=20×6,改写成比例是 。
36.(2024六下·大余期中)0.4立方米= 升
1600毫升= 立方分米
10.4平方米= 平方米 平方分米
5时40分= 时
37.(2024六下·鹰潭期中)一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作 千米;+10千米表示 。
38.(2024六下·大余期中)把一根长10dm的圆柱形钢柱截成两段,表面积比原来增加:,这根圆柱原来的体积是 dm3。
39.(2024六下·大余期中)等底等高的圆柱和圆锥体,它们的体积之和是150立方米,圆锥的体积是 立方米。
40.(2024六下·南昌期中)在一幅地图上,20cm的长度表示实际距离18km,这幅地图的比例尺是 ,如果甲,乙两地之间的实际距离4.5km,那么在这幅地图上应该用 cm来表示。
41.(2024六下·南昌期中)一个圆柱体,底面周长是31.4cm,高6cm,它的表面积是 cm2,体积是 cm3。
42.(2024六下·南昌期中)一辆自行车原价350元,打九折后是 元,另一辆自行车打九折后是270元,这辆自行车的原价是 元。
43.(2024六下·鹰潭期中)在中,图中1cm表示实际距离 km,改写成数值比例尺是 。
44.(2024六下·南昌期中)圆柱的底面半径和高都扩大到原来的2倍,则它的底面积扩大到原来的 倍,体积扩大到原来的 倍。
45.(2024六下·大余期中)在比例尺为1:5000000的地图上,南昌、广州两地相距16cm,在另一幅比例尺为1:4000000的地图上,南昌、广州两地相距 厘米。
46.(2024六下·南昌期中)x,y都不为0,,则x和y成 比例,若9m=7n,则m和n成 比例。
47.(2024六下·大余期中)一个直角三角形的两条直角边分别为6cm,10cm,若以6cm的边为轴旋转一周,所围图形的体积是 cm3。
48.(2024六下·鹰潭期中)把一个棱长是6cm的正方体削成一个最大的圆锥体,这个圆锥的体积是 。
49.(2024六下·大余期中)0.6:3= :18= = %
50.(2024六下·大余期中)天虹超市举行“五一”商品大推销,有一套“”玩具打九折出售,“九折”表示现价相当于原价的 %,如果这件玩具现价卖72元,那么原价是 。
答案解析部分
1.6:3=4:2,3:6=2:4,2:3=4:6,3:2=6:4;4
解:可以改成的比例有:6:3=4:2,3:6=2:4,2:3=4:6,3:2=6:4,
共可以组成4个不同的比例。
故答案为:6:3=4:2,3:6=2:4,2:3=4:6,3:2=6:4;4。
两个比只要比值相等,就可以组成比例,据此解答。
2.62.5;5;5:8
解:0.625==62.5%==5:8。
故答案为:62.5;5;5:8。
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;
小数化分数:小数点后有几位小数,就在1后面添几个0做分母,小数点去掉做分子。能约分的要约成最简分数;分数可以写成比的形式,分子是比的前项,分母是比的后项。
3.16立方分米
解:48÷3=16(立方分米)。
故答案为:16立方分米。
与圆柱等底等高的圆锥的体积=圆柱的体积÷3。
4.314cm2
解:3.14×10×10=314(cm2)
故答案为:314cm2。
圆柱的侧面积=底面周长×高,根据公式计算圆柱的侧面积即可。
5.64
解:8×4×2
=32×2
=64(cm2)
故答案为:64。
圆柱切开后的一个切面是一个长方形,增加的面积就是2个长是8cm,宽是4cm的长方形的面积。
6.314
解:6.28÷3.14÷2=1(分米)
3.14×1×100
=3.14×100
=314(立方分米)
故答案为:314。
孙悟空的如意金箍棒如果是圆柱形,圆柱的体积 = π × (底面半径的平方) × 高;据此代入数值计算。
7.妈妈能获得利息多少元;80000×3×1.95%
解:问题:妈妈能获得利息多少元?
本金是80000元,年利率是1.95%,存款时间为三年,所以利息为:80000×3×1.95%(元)。
故答案为:妈妈能获得利息多少元; 80000×3×1.95%。
利息=本金×利率×存款时间;据此提出问题列出算式。
8.反
解:由=可得:xy=8×5=40, x和y成反比例。
故答案为:反。
比例的基本性质:比例的外项之积等于比例的内项之积;
反比例的判断方法:相关联,能变化,积一定。
9.1:2=2:4
解:写出两个比值都是的比,再组成比例是1:2=2:4。
故答案为:1:2=2:4(答案不唯一)。
比例是表示两个比相等的式子。由此写出两个比值是的比,再组成比例即可。
10.0;-3℃
解:0既不是正数,也不是负数,零下3℃记作-3℃。
故答案为:0;-3℃。
正负数表示相反意义的量,高于0℃的温度记作正,低于0℃的温度就记作负。
11.比例的基本性质
解:在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
故答案为:比例的基本性质。
比例的基本性质:在比例里,两个内项积等于两个外项积。
12.3;2;b;8
解:a:b=12:8=3:2;a:12=b:8。
故答案为:3;2;b;8。
比例的基本性质:在一个比例中,两个外项的积等于两个内项的积。如果a是外项,b是内项,则8为外项,12为内项,在化简比。如果a是外项,12是内项,则8为外项,b为内项。
13.44;32;0;+11
解:第一空:39+5=44(千克)
第二空:39-7=32(千克)
第三空:39-39=0(千克)
第四空:50-39=11(千克)
学号 1 2 3 4 5
体重(千克) 35 44 39 50 32
与平均体重相比(千克) ﹣4 +5 0 +11 ﹣7
故答案为:44;32;0;+11。
比39千克多的质量用正数表示,比39千克少的质量用负数表示,正数表示比39千克多的质量,负数表示比39千克少的质量,据此解答。
14.正
解:乒乓球的总个数÷需要的盒数=每盒乒乓球的个数(一定),
乒乓球的总个数和需要的盒数成正比例。
故答案为:正。
正比例的判断方法:相关联,能变化,商一定。
15.4
解:﹣8,﹣11,0,96都是整数,有4个。
故答案为:4。
整数包括正整数、0、负整数。
16.﹣20米
解:如果前进30米记作+30米,那么后退20米记作-20米。
故答案为:-20米。
前进用正数表示,后退就用负数表示。
17.-130
解:零上27℃,可以记为+27℃,零下130℃,可以记为-130℃。
故答案为:-130。
零上温度用正数表示,零下温度用负数表示。
18.31.4;20
解:2×π×5
=2×3.14×5
=31.4(cm)
圆柱的高即为商标纸的宽,为20cm。
故答案为:31.4;20。
圆柱的侧面展开后是一个长方形,其长等于圆柱底面的周长,宽等于圆柱的高;圆柱的底面积:S=r2。
19.圆柱的高
解:圆柱的两个底面圆心之间的距离叫作圆柱的高。
故答案为:圆柱的高。
圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条。
20.24:8=9:3;8:3=24:9
解:可以写出比例24:8=9:3或者8:3=24:9(答案不唯一)。
故答案为:24:8=9:3;8:3=24:9。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此写比例。
21.反;15;5
解:反比例图像是一条光滑的曲线;
当高度是20cm,底面积是300÷20=15(cm2);
当底面积是55cm2时,高度是:300÷55≈5(cm)
故答案为:反;15;5。
反比例指的是两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
22.480
解:表面积比原来增加了2个长方形,
16×15×2
=240×2
=480(平方厘米)
表面积比原来增加480平方厘米。
故答案为:480。
底面直径×长=增加的一个面的面积,增加的一个面的面积×2=增加的面积。
23.4;-4;8℃
解:4-(-4℃)=8℃
这天的最高气温是4℃,最低气温是-4℃,温差是8℃。
故答案为:4;-4;8℃。
气温高于0℃记作正,则低于0℃就记作负。用最高气温减去最低气温求出温差。
24.20000;30
比例尺是1:2000000,表示地图上1cm代表实际距离2000000cm,换成m做单位后就是20000m;
600km=60000000cm,60000000×=30(cm)。
故答案为:20000m;30cm。
图上距离:实际距离=比例尺(1:2000000 ) ,就是表示图上1cm代表实际距离2000000cm,但题中的单位是m,所以还要注意化好单位即可;图上距离=实际距离×比例尺(比例尺的分数形式),先将实际距离化成用cm做单位再去求解即可。
25.5;3
解:3a=5b,那么a:b=5:3。
故答案为:5;3。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此解答。
26.1;30;40;0.4;四;四
解:1.6:4=1.6÷4=0.4
2.5×0.4=1;
12÷0.4=30;
0.4=40%=四折=四成;
所以1.6:4=1:2.5==40%=0.4=四折=四成。
故答案为:1;30;40;0.4;四;四。
求比值=比的前项÷比的后项,比的前项=比的后项×比值;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;
百分数与折扣的互化,百分之几十就是几折;百分之几十就等于几成。
27.8;226.08
解:3.14×(6÷2)2=28.26(cm2)
75.36÷÷28.26
=226.08÷28.26
=8(cm)
75.36×3=226.08(cm3)
故答案为:8;226.08。
πr2=圆锥的底面积,圆锥的体积÷÷底面积=圆锥的高;
根据圆柱与圆锥体积的关系可知:等底等高的圆柱的体积是圆锥体积的3倍,据此可以解答。
28.10:1
解:图上距离是5cm,转换为毫米是5cm ×10 = 50mm,
5cm:5mm
=50mm:5mm
=10:1
故答案为:10:1。
比例尺=图上距离:实际距离;先进行单位换算,再求出比例尺。
29.31.5
解:10.5×3=31.5(立方厘米)
和它等底等高的圆柱的体积是31.5立方厘米
故答案为:31.5。
等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
30.
解:在一个比例里,两个内项互为倒数,
可知两个外项也互为倒数,其中一个外项是3,所以另一个外项就是3的倒数 .
故答案为: .
由“在一个比例里,两个内项互为倒数”,根据比例的性质“两外项的积等于两内项的积”,可知两个外项也互为倒数;再根据“其中一个外项是3”,进而求出3的倒数得解.
31.25.12cm
解:3.14×8=25.12(cm)
故答案为:25.12cm。
圆柱的侧面展开是正方形,那么圆柱的高与底面周长相等,所以计算出圆柱的底面周长就是这个圆柱的高。
32.20;28;七五
解:15÷0.75=20,21÷0.75=28,所以15:20=0.75=21÷28=七五折。
故答案为:20;28;七五。
比值和商都是0.75,可以用前项除以比值求出后项,用被除数除以商求出除数;把小数化成百分数再确定折扣。
33.;
解:则ab=5c,ab=1,所以5c=1,则c=;
=×=。
故答案为:;。
根据比例的基本性质把这个比例写成两个內项积等于两个外项积的行驶,a与b互为倒数,则a、b的积是1,这样就能求出c的值,然后求出的值即可。
34.180
解:15×12=180(平方厘米)
故答案为:180。
根据圆柱的侧面展开图的特点:圆柱的底面周长是长方形的长,圆柱的高是长方形的宽,所以这个圆柱的侧面积就是这个长方形的面积;用长乘宽即可。
35.3:20=6:40
解:把3×40=20×6,改写成比例是3:20=6:40。
故答案为:3:20=6:40。(答案不唯一)
在比例里,两个內项的积等于两个外项的积。把3和40作为外项,20和6就是內项,然后写出比例即可。
36.400;1.6;10;40;
解:0.4×1000=400,0.4立方米=400升;
1600÷1000=1.6,1600毫升=1.6立方分米;
0.4×100=40,10.4平方米=10平方米40平方分米;
40÷60=,5时40分=时。
故答案为:400;1.6;10,40;。
1立方米=1000立方分米,1升=1000毫升, 1升=1立方分米, 1平方米=100平方分米,1小时=60分,单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
37.-20;向东行10千米
解:一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作-20千米;+10千米表示向东行10千米。
故答案为:-20;向东行10千米。
以学校为起点,向东走记作正,向西走记作负。根据正负数的意义填空即可。
38.0.18
解:10dm=100cm
3.6÷2×100
=1.8×100
=180(立方厘米)
180立方厘米=0.18立方分米
故答案为:0.18。
把一根长10dm的圆柱形钢柱截成两段 ,增加了2个面,每个面积都是圆柱的底面积,用3.6除以2求出圆柱的底面积,再根据圆柱的体积公式V=Sh,求出圆柱的体积,再换算单位。
39.37.5
解:150÷(3+1)
=150÷4
=37.5(立方米)
故答案为:37.5。
等底等高的圆柱的体积是圆锥体积的3倍,它们的体积之和是(3+1)倍,由此计算圆锥的体积即可。
40.1:90000;5
解:18km=1800000cm,20:1800000=1:900000;
4.5km=450000cm,450000×=5(cm)。
故答案为:1:90000;5。
图上距离:实际距离=比例尺,图上距离=实际距离×比例尺,1km=100000cm。
41.345.4;471
解:半径:31.4÷3.14÷2=5(厘米),表面积:31.4×6+2×3.14×52=345.4(平方厘米);体积:3.14×52×6=471(立方厘米)。
故答案为:345.4;471。
半径=圆的周长÷π÷2;圆柱的表面积=2×底面积+侧面积,其中底面积=π×半径2;侧面积=底面周长×高;圆柱的体积=π×半径2×高。
42.315;300
解:现价:350×90%=315(元);原价:270÷90%=300(元)。
故答案为:315;300。
在折扣问题中,现价与原价的关系为:现价=原价×折扣。
43.40;1:4000000
解:在中,图中1cm表示实际距离40km,改写成数值比例尺是1cm:40km=1cm:4000000cm=1:4000000。
故答案为:40;1:4000000。
线段比例尺表示图上1厘米相当于实际距离40千米。写出图上距离与实际距离的比,统一单位后写成前项是1的比就可以改写成数值比例尺。
44.4;8
解:假设圆柱的底面半径和高都为1,则扩大后都为2,扩大后的底面积为:,扩大后的体积为:。
故答案为:4;8。
圆的面积=π×半径2;圆柱的体积=π×半径2×高。
45.20
解:16÷=80000000(厘米)
80000000×=20(厘米)
故答案为:20。
依据“实际距离=图上距离÷比例尺”即可求出南昌、广州两地的实际距离,再根据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离。
46.反;正
解:xy=8(一定),乘积一定,成反比例关系;m:n=7:9(一定),比值一定,成正比例关系。
故答案为:反;正。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的比值(或商)一定,那么它们的关系称为正比例关系。
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,这两种量就叫做反比例的量。它们的关系称为反比例关系。
47.628
解:3.14×102×6×
=314×6×
=314×2
=628(立方厘米)
故答案为:628。
将这个直角三角形以6厘米为轴旋转一周,可得到一个以6厘米为高、以10厘米为底面半径的圆锥体,根据圆锥的体积公式V=sh进行计算。
48.56.52cm3
解:3.14×(6÷2)2×6×
=3.14×9×2
=56.52(cm3)
故答案为:56.52cm3。
把这个正方体削成最大的圆锥,圆锥的底面直径和高都与正方体的棱长相等。圆锥的体积=底面积×高×,根据公式计算圆锥的体积即可。
49.3.6;90;20
解:0.6×6=3.6
3×30=90
18÷90=0.2=20%
0.6:3=3.6:18==20%
故答案为:3.6;90;20。
根据比的基本性质,0.6:3的前、后项都乘6就是3.6:18;根据比与分数的关系0.6:3=,根据分数的基本性质,分子、分母都乘30就是;18÷90=0.2,0.2改写成百分数是20%。
50.90;80
解: “九折”表示现价相当于原价的90%。
72÷90%=80(元)
故答案为:90;80。
打几折,表示现价是原价的百分之几十;用现价÷折扣=原价。
同课章节目录
