2025年数学中考专题一轮复习课件:4.20 全等三角形(共36张PPT)
文档属性
| 名称 | 2025年数学中考专题一轮复习课件:4.20 全等三角形(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 11:04:39 | ||
图片预览









文档简介
(共36张PPT)
2025年数学中考复习
4.20 全等三角形
基础知识
项目四 三角形
考点要求
壹
1.理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
2.掌握基本事实:
(1)两边及其夹角分别相等的两个三角形全等;
(2)两角及其夹边分别相等的两个三角形全等;
(3)三边分别相等的两个三角形全等.
3.证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
4.探索并掌握判定直角三角形全等的“斜边、直角边”定理.
核心知识点
贰
概念
能够完全重合的两个三角形叫作全等三角形.
性质
(1)全等三角形的对应边 ,对应角 ;
(2)全等三角形的周长 ,面积 ;
(3)全等三角形对边上的中线、高线、中位线 .
知识点1 全等三角形的概念及性质
相等
相等
相等
相等
相等
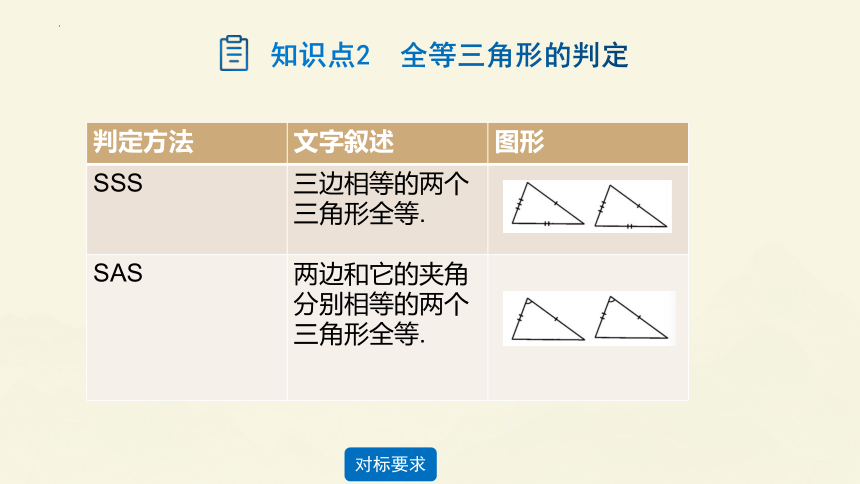
判定方法 文字叙述 图形
SSS 三边相等的两个三角形全等.
SAS 两边和它的夹角分别相等的两个三角形全等.
知识点2 全等三角形的判定
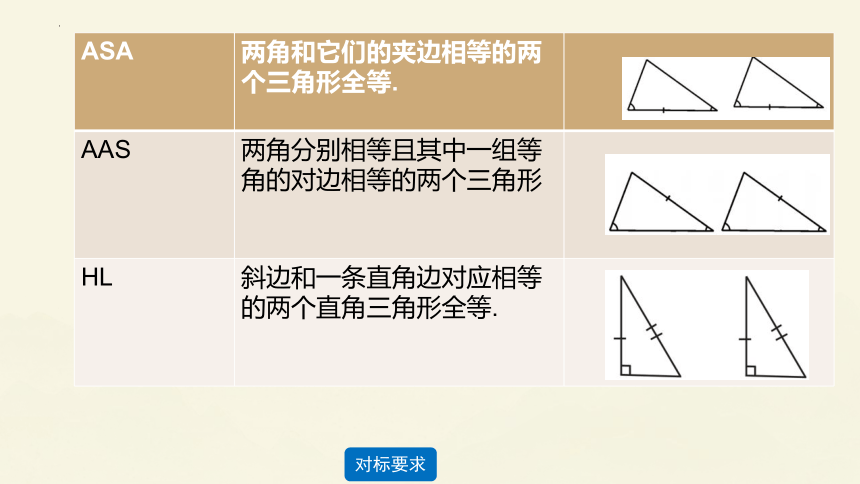
ASA 两角和它们的夹边相等的两个三角形全等.
AAS 两角分别相等且其中一组等角的对边相等的两个三角形
HL 斜边和一条直角边对应相等的两个直角三角形全等.
【归纳】判定两个三角形全等常用的思路方法如下:
考点攻坚
叁
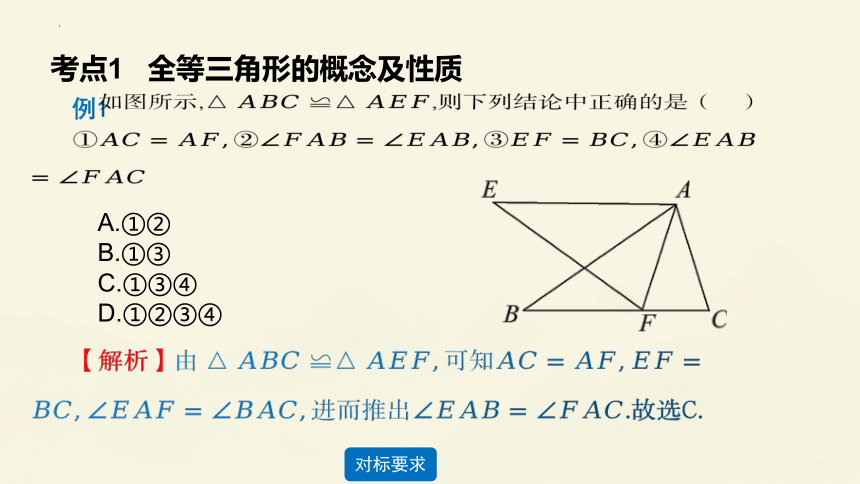
考点1 全等三角形的概念及性质
例1
如图所示,,则下列结论中正确的是( )
【解析】.故选C.
A.①②
B.①③
C.①③④
D.①②③④
(2024·大理)数学社团活动课上,甲乙两位同学玩数学游戏.游戏规则是:两人轮流对及的对应边或对应角添加一组等量条件(点分别是点的对应点),某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.
考点2 全等三角形的判定
例2
轮次 行动者 添加条件
1 甲 AB==2cm
2 乙 ∠A==35°
3 甲 ……
表格记录了两人游戏的部分过程,则下列说法正确的是( )
①若第3轮甲添加cm,则甲必胜;
②若第3轮甲添加,则甲获胜;
③若第2轮乙添加条件修改为,则乙必胜;
④若第2轮乙添加条件修改为cm,则此游戏最多四轮必分胜负.
A.①③ B.②④ C.①④ D.③④
【解析】解:①若第3轮甲添加cm,满足边边角,不能判定与全等,则甲获胜,正确,符合题意;
②若第3轮甲添加,可根据角角边判定全等,则乙获胜,不符合题意;
③若第2 轮乙添加条件修改为,若第3轮甲添加一边相等,可根据边角边或斜边直角边判定全等,则乙获胜,若第3轮甲添加一角相等,可根据角角边或角边角判定全等,则乙获胜,故乙必胜,故本说法正确,符合题意;
④若第2轮乙添加条件修改为cm,第3轮甲只能添加或其中之一,此时已有边边角.无论第4轮乙添加对应边相等还是对应角相等,都会有边边边或角角边或角边角来判定出全等,则乙必输,甲必胜.所以最多4轮必分胜负,本说法正确,不符合题意.
故选D.
专项训练
肆
达标训练
1.(2022·宁波)如图所示,的依据是( )
A.SSS
B.SAS
C.AAS
D.HL
B
2.(2022·黑龙江 )如图所示,,与交于点,请添加一个条件 ,使(只填写一种情况即可).
过关训练
3.(2022·台州)如图所示,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,他将该三角形记为.下列提供的各组元素的数据,配出来的玻璃不一定符合要求的是(C )
A.
B.
C.
D.
4.(2024·贵阳)如图,在平行四边形中,边上一点,的延长线上,且.
(1)求证:;
(2)若,点的中点,求的长.
答案
5.(2024·甘肃)小明同学在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,表示小球静止时的位置.当小明用发声物体靠近小球时,小球从位置,此时过点于点,当小球摆到位置时,恰好垂直(图中的在同一平面上),过点,测得cm,cm.
(1)求证:;
(2)求的长.
5.解:(1)证明:∵OB OC,
∴∠BOD+∠COE=90°,
∵BD OA,∴∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B;
(2)解:∵BD OA,CE OA,
∴∠CEO=∠ODB=90°。
答案
由题意得:OC=OB=OA=17 cm,
由(1)得:∠COE=∠B,
∠CEO=∠ODB
在△COE和△OBD中,∠COE=∠BOC=∠B
∴△COE≌△OBD(AAS),
∴OE=BD=8 cm,
∴AE=OA-OE=17-8=9 cm.
课堂练习
伍
1.(2024·庐山)如图所示,点、点在上,,,添加一个条件,不能证明≌的是(D)
A.
B.
C.
D.
2.如图所示,,点是对应顶点,点是对应顶点,过点,垂足为点,若,则的度数为( )
A.30° B.25° C.35° D.65°
B
3.(2023·丹东)如图所示,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点的中点,只要量出的长度,就可以知道该零件内径的长度.依据的数学基本事实是(A )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所得的对应线段成比例
D.两点之间线段最短
4.已知△与△全等,,,的对应点分别为,,,且点在上,,,,四点共线,如图所示.若,,则下列叙述正确的是( )
A.,
B.,
C.,
D.,
B
5.(2022·鄂尔多斯)如图所示,在四边形中,对角线相交于点若添加一个条件 ,则可使.
6.如图所示是由四个相同的小正方形组成的网格图,则 .
(答案不唯一)
180°
7.(2023·大连)如图所示,在中,,点的中点,过点交的延长线于点,若,则的长为 .
8.(2023·扬州)如图所示,在中,,为的角平分线.以点圆心,长为半径画弧,与,分别交于点,,连接,.
(1)求证:;
(2)若,求的度数.
答案
8.(1)证明:∵是的角平分线,∴
由作图知,.
在△和△中,
∴△≌△().
(2)∵,为△的角平分线,
∴.由作图知,.∴.∴.
∵,为△的角平分线,∴.∴.
9.(2023·曲阜)如图所示,在四边形中,点是边上一点,且,.
(1)求证:;
(2)若,时,求△的面积.
9.(1)证明:∵,
∴,即,∴,
在△和△中,∴△≌△().
∴.∴;
答案
(2)解:过点,由(1)知,∵,
∴,∵.∴,∴
,∴.
10.▲跨学科(2024·黄冈)小明同学在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,表示小球静止时的位置.当小明用发声物体靠近小球时,小球从位置,此时过点于点,当小球摆到位置时,恰好垂直(图中的在同一平面上),过点,测得cm,cm.
(1)求证:;
(2)求的长.
答案
谢谢观看
2025年数学中考复习
4.20 全等三角形
基础知识
项目四 三角形
考点要求
壹
1.理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
2.掌握基本事实:
(1)两边及其夹角分别相等的两个三角形全等;
(2)两角及其夹边分别相等的两个三角形全等;
(3)三边分别相等的两个三角形全等.
3.证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
4.探索并掌握判定直角三角形全等的“斜边、直角边”定理.
核心知识点
贰
概念
能够完全重合的两个三角形叫作全等三角形.
性质
(1)全等三角形的对应边 ,对应角 ;
(2)全等三角形的周长 ,面积 ;
(3)全等三角形对边上的中线、高线、中位线 .
知识点1 全等三角形的概念及性质
相等
相等
相等
相等
相等
判定方法 文字叙述 图形
SSS 三边相等的两个三角形全等.
SAS 两边和它的夹角分别相等的两个三角形全等.
知识点2 全等三角形的判定
ASA 两角和它们的夹边相等的两个三角形全等.
AAS 两角分别相等且其中一组等角的对边相等的两个三角形
HL 斜边和一条直角边对应相等的两个直角三角形全等.
【归纳】判定两个三角形全等常用的思路方法如下:
考点攻坚
叁
考点1 全等三角形的概念及性质
例1
如图所示,,则下列结论中正确的是( )
【解析】.故选C.
A.①②
B.①③
C.①③④
D.①②③④
(2024·大理)数学社团活动课上,甲乙两位同学玩数学游戏.游戏规则是:两人轮流对及的对应边或对应角添加一组等量条件(点分别是点的对应点),某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.
考点2 全等三角形的判定
例2
轮次 行动者 添加条件
1 甲 AB==2cm
2 乙 ∠A==35°
3 甲 ……
表格记录了两人游戏的部分过程,则下列说法正确的是( )
①若第3轮甲添加cm,则甲必胜;
②若第3轮甲添加,则甲获胜;
③若第2轮乙添加条件修改为,则乙必胜;
④若第2轮乙添加条件修改为cm,则此游戏最多四轮必分胜负.
A.①③ B.②④ C.①④ D.③④
【解析】解:①若第3轮甲添加cm,满足边边角,不能判定与全等,则甲获胜,正确,符合题意;
②若第3轮甲添加,可根据角角边判定全等,则乙获胜,不符合题意;
③若第2 轮乙添加条件修改为,若第3轮甲添加一边相等,可根据边角边或斜边直角边判定全等,则乙获胜,若第3轮甲添加一角相等,可根据角角边或角边角判定全等,则乙获胜,故乙必胜,故本说法正确,符合题意;
④若第2轮乙添加条件修改为cm,第3轮甲只能添加或其中之一,此时已有边边角.无论第4轮乙添加对应边相等还是对应角相等,都会有边边边或角角边或角边角来判定出全等,则乙必输,甲必胜.所以最多4轮必分胜负,本说法正确,不符合题意.
故选D.
专项训练
肆
达标训练
1.(2022·宁波)如图所示,的依据是( )
A.SSS
B.SAS
C.AAS
D.HL
B
2.(2022·黑龙江 )如图所示,,与交于点,请添加一个条件 ,使(只填写一种情况即可).
过关训练
3.(2022·台州)如图所示,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,他将该三角形记为.下列提供的各组元素的数据,配出来的玻璃不一定符合要求的是(C )
A.
B.
C.
D.
4.(2024·贵阳)如图,在平行四边形中,边上一点,的延长线上,且.
(1)求证:;
(2)若,点的中点,求的长.
答案
5.(2024·甘肃)小明同学在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,表示小球静止时的位置.当小明用发声物体靠近小球时,小球从位置,此时过点于点,当小球摆到位置时,恰好垂直(图中的在同一平面上),过点,测得cm,cm.
(1)求证:;
(2)求的长.
5.解:(1)证明:∵OB OC,
∴∠BOD+∠COE=90°,
∵BD OA,∴∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B;
(2)解:∵BD OA,CE OA,
∴∠CEO=∠ODB=90°。
答案
由题意得:OC=OB=OA=17 cm,
由(1)得:∠COE=∠B,
∠CEO=∠ODB
在△COE和△OBD中,∠COE=∠BOC=∠B
∴△COE≌△OBD(AAS),
∴OE=BD=8 cm,
∴AE=OA-OE=17-8=9 cm.
课堂练习
伍
1.(2024·庐山)如图所示,点、点在上,,,添加一个条件,不能证明≌的是(D)
A.
B.
C.
D.
2.如图所示,,点是对应顶点,点是对应顶点,过点,垂足为点,若,则的度数为( )
A.30° B.25° C.35° D.65°
B
3.(2023·丹东)如图所示,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点的中点,只要量出的长度,就可以知道该零件内径的长度.依据的数学基本事实是(A )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所得的对应线段成比例
D.两点之间线段最短
4.已知△与△全等,,,的对应点分别为,,,且点在上,,,,四点共线,如图所示.若,,则下列叙述正确的是( )
A.,
B.,
C.,
D.,
B
5.(2022·鄂尔多斯)如图所示,在四边形中,对角线相交于点若添加一个条件 ,则可使.
6.如图所示是由四个相同的小正方形组成的网格图,则 .
(答案不唯一)
180°
7.(2023·大连)如图所示,在中,,点的中点,过点交的延长线于点,若,则的长为 .
8.(2023·扬州)如图所示,在中,,为的角平分线.以点圆心,长为半径画弧,与,分别交于点,,连接,.
(1)求证:;
(2)若,求的度数.
答案
8.(1)证明:∵是的角平分线,∴
由作图知,.
在△和△中,
∴△≌△().
(2)∵,为△的角平分线,
∴.由作图知,.∴.∴.
∵,为△的角平分线,∴.∴.
9.(2023·曲阜)如图所示,在四边形中,点是边上一点,且,.
(1)求证:;
(2)若,时,求△的面积.
9.(1)证明:∵,
∴,即,∴,
在△和△中,∴△≌△().
∴.∴;
答案
(2)解:过点,由(1)知,∵,
∴,∵.∴,∴
,∴.
10.▲跨学科(2024·黄冈)小明同学在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,表示小球静止时的位置.当小明用发声物体靠近小球时,小球从位置,此时过点于点,当小球摆到位置时,恰好垂直(图中的在同一平面上),过点,测得cm,cm.
(1)求证:;
(2)求的长.
答案
谢谢观看
同课章节目录
