浙江省宁波市2024-2025学年第二学期九年级三月联考数学试卷(无答案)
文档属性
| 名称 | 浙江省宁波市2024-2025学年第二学期九年级三月联考数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 321.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 13:43:30 | ||
图片预览


文档简介
2024 学年第二学期九年级三月联考数学学科试卷
一、 选择题 (每题 3 分, 共 30 分)
1. -2025 的绝对值是( )
A. 2025 B. C. -2025 D.
2. 下列计算正确的是( )
A. B. C. D.
3. 截止到 3 月 1 日为止,动画电影《哪吒之魔童闹海》票房收入已超过 145 亿元. 数 145 亿用科学记数法表示为( )
A. B. C. D.
4. 拓展课上有同学设计了艺术字 “中国”,下面展示如图几何体 “中” 字的俯视图是 ( )
A. B. C. D.
5. 若代数式 有意义,则 的取值范围是( )
A. B. C. D.
6. 一个圆锥的底面直径是 8 ,母线长是 7 ,则圆锥的侧面积是( )
A. B. C. D.
7. 如图,分别以点 为圆心,大于 的长为半径作弧,交点分别为 ,连结 交 于点 ,下列说法一定正确的是 ( )
A. 是直角三角形 B. 是等腰三角形
C. 是等腰三角形 D. 是等腰三角形
8. 若关于 的一元二次方程 的解为 ,则关于 的一元二次方程 的解为( )
A. B.
C. D.
9. 我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托, 对折索子来量竿, 却比竿子短一托 (一托按照 5 尺计算)。” 大意是: 现有一根竿子和一条绳索, 如果用绳索去量竿子, 绳索比竿长 5 尺; 如果将绳索对折后再去量竿子,就比竿短 5 尺。则绳索长几尺 设竿子长 尺,绳索长 尺,根据题意可列方程组为( )
A. B. C. D.
10. 如图,矩形 中, 为对角线 上一点,过 分别作 、 的平行线于矩形边相交, 若矩形 ABCD 的面积为 S, 则阴影部分的面积可以表示为( )
A. B. C. D.
第七题图 第十题图
二、填空题(每题 3 分,共 18 分)
11. 若分式 的值为零,则 _____。
12. 分解因式: _____。
13. 一个布袋里装有 6 个只有颜色不同的球, 其中有 4 个红球. 2 个白球, 从布袋里随机摸出 1 个球,则摸出白球的概率为_____。
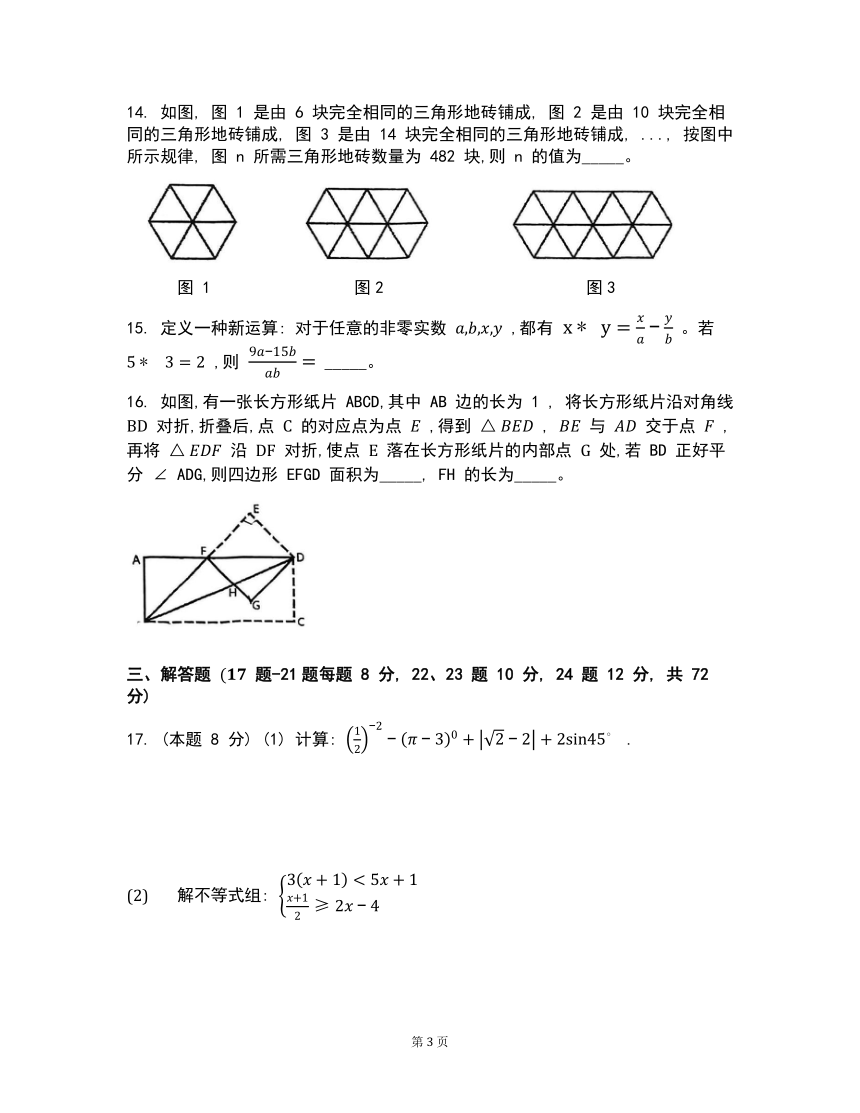
14. 如图, 图 1 是由 6 块完全相同的三角形地砖铺成, 图 2 是由 10 块完全相同的三角形地砖铺成, 图 3 是由 14 块完全相同的三角形地砖铺成, ..., 按图中所示规律, 图 n 所需三角形地砖数量为 482 块,则 n 的值为_____。
图 1 图2 图3
15. 定义一种新运算: 对于任意的非零实数 ,都有 。若 ,则 _____。
16. 如图,有一张长方形纸片 ABCD,其中 AB 边的长为 1 , 将长方形纸片沿对角线 对折,折叠后,点 的对应点为点 ,得到 , 与 交于点 ,再将 沿 对折,使点 落在长方形纸片的内部点 处,若 BD 正好平分 ADG,则四边形 EFGD 面积为_____, FH 的长为_____。
三、解答题 题-21题每题 8 分, 22、23 题 10 分, 24 题 12 分, 共 72 分)
17. (本题 8 分) (1) 计算: .
解不等式组:
18. (本题 8 分) 如图,方格纸中的每个小正方形的边长都是 1 , 是格点三角形 (顶点在方格顶点处).
(1)在图 1 中画出一个格点 ,使得 与 相似,周长之比为 2: 1;
(2)在图 2 中画出一个格点 ,使得 与 相似,面积之比为 2:1.
19. (本题 8 分) 生活经验表明, 靠墙摆放的梯子,当 ( 为梯子与地面所成的角), 能够使人安全攀爬, 现在有一长为 的梯子 ,试求能够使人安全攀爬时, 梯子的顶端能达到的最大高度 . (结果保留两个有效数字, , ,
20. (本题 8 分)某地为提倡节约用水,准备实行自来水 “阶梯计费” 方式, 用户用水不超出基本用水量的部分享受基本价格, 超出基本用水量的部分实行加价收费, 为更好地决策, 自来水公司随机抽取部分用户的用水量数据, 并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中 “ 25 吨” 30 吨” 部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户 25 吨,那么该地 20 万用户中约有多少用户的用水全部享受基本价格
21. (本题 8 分)如图, 的直径 于点 ,且 是半径 OB 的中点, CD=8cm,
(1). 求直径 的长.
( 2 ). 求弓形( 阴影部分)的面积
22. (本题 10 分) 二次函数 的图象经过点(4, - 2),且对称轴为直线
( 1 )求这个二次函数的解析式.
(2)图象上的点(x, x)称为函数的不动点,求这个函数不动点的坐标.
(3)若 是二次函数图象上不动点之间的点(包括端点),求 的最大值与最小值的差.
23. (本题 10 分) 今年假期,你有没有和父母或者小伙伴一起走进影院去看一下国漫电影《哪吒 2》呀!影片中,玉虚宫的镇宫之宝 “天元鼎” 大到超乎想象,存放它的建筑是一座 “正八边形” 的宫殿,你想知道这座建筑有多大吗?
问题一:要求出 “正八边形” 的面积,我们可以把一个 “正八边形” 均分成八个顶角为_____度的等腰三角形。
问题二: 中, , , . 求 的面积和 的值分别是多少
(可以作 的中垂线 交 于 ,交 于 ,则 为等腰三角形, )
问题三:若“正八边形”的边长 为 ,求: 正八边形的面积。
24. (本题 12 分)如图,矩形 中,点 在 上, 与 相交于点 0.BE.与 相交于点 .
(1)若 平分 ,求证: 是等边三角形;
(2)找出图中一个与 相似的三角形,并说明理由;
(3)若 ,求 的长度.
(
第
1
页
)
一、 选择题 (每题 3 分, 共 30 分)
1. -2025 的绝对值是( )
A. 2025 B. C. -2025 D.
2. 下列计算正确的是( )
A. B. C. D.
3. 截止到 3 月 1 日为止,动画电影《哪吒之魔童闹海》票房收入已超过 145 亿元. 数 145 亿用科学记数法表示为( )
A. B. C. D.
4. 拓展课上有同学设计了艺术字 “中国”,下面展示如图几何体 “中” 字的俯视图是 ( )
A. B. C. D.
5. 若代数式 有意义,则 的取值范围是( )
A. B. C. D.
6. 一个圆锥的底面直径是 8 ,母线长是 7 ,则圆锥的侧面积是( )
A. B. C. D.
7. 如图,分别以点 为圆心,大于 的长为半径作弧,交点分别为 ,连结 交 于点 ,下列说法一定正确的是 ( )
A. 是直角三角形 B. 是等腰三角形
C. 是等腰三角形 D. 是等腰三角形
8. 若关于 的一元二次方程 的解为 ,则关于 的一元二次方程 的解为( )
A. B.
C. D.
9. 我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托, 对折索子来量竿, 却比竿子短一托 (一托按照 5 尺计算)。” 大意是: 现有一根竿子和一条绳索, 如果用绳索去量竿子, 绳索比竿长 5 尺; 如果将绳索对折后再去量竿子,就比竿短 5 尺。则绳索长几尺 设竿子长 尺,绳索长 尺,根据题意可列方程组为( )
A. B. C. D.
10. 如图,矩形 中, 为对角线 上一点,过 分别作 、 的平行线于矩形边相交, 若矩形 ABCD 的面积为 S, 则阴影部分的面积可以表示为( )
A. B. C. D.
第七题图 第十题图
二、填空题(每题 3 分,共 18 分)
11. 若分式 的值为零,则 _____。
12. 分解因式: _____。
13. 一个布袋里装有 6 个只有颜色不同的球, 其中有 4 个红球. 2 个白球, 从布袋里随机摸出 1 个球,则摸出白球的概率为_____。
14. 如图, 图 1 是由 6 块完全相同的三角形地砖铺成, 图 2 是由 10 块完全相同的三角形地砖铺成, 图 3 是由 14 块完全相同的三角形地砖铺成, ..., 按图中所示规律, 图 n 所需三角形地砖数量为 482 块,则 n 的值为_____。
图 1 图2 图3
15. 定义一种新运算: 对于任意的非零实数 ,都有 。若 ,则 _____。
16. 如图,有一张长方形纸片 ABCD,其中 AB 边的长为 1 , 将长方形纸片沿对角线 对折,折叠后,点 的对应点为点 ,得到 , 与 交于点 ,再将 沿 对折,使点 落在长方形纸片的内部点 处,若 BD 正好平分 ADG,则四边形 EFGD 面积为_____, FH 的长为_____。
三、解答题 题-21题每题 8 分, 22、23 题 10 分, 24 题 12 分, 共 72 分)
17. (本题 8 分) (1) 计算: .
解不等式组:
18. (本题 8 分) 如图,方格纸中的每个小正方形的边长都是 1 , 是格点三角形 (顶点在方格顶点处).
(1)在图 1 中画出一个格点 ,使得 与 相似,周长之比为 2: 1;
(2)在图 2 中画出一个格点 ,使得 与 相似,面积之比为 2:1.
19. (本题 8 分) 生活经验表明, 靠墙摆放的梯子,当 ( 为梯子与地面所成的角), 能够使人安全攀爬, 现在有一长为 的梯子 ,试求能够使人安全攀爬时, 梯子的顶端能达到的最大高度 . (结果保留两个有效数字, , ,
20. (本题 8 分)某地为提倡节约用水,准备实行自来水 “阶梯计费” 方式, 用户用水不超出基本用水量的部分享受基本价格, 超出基本用水量的部分实行加价收费, 为更好地决策, 自来水公司随机抽取部分用户的用水量数据, 并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中 “ 25 吨” 30 吨” 部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户 25 吨,那么该地 20 万用户中约有多少用户的用水全部享受基本价格
21. (本题 8 分)如图, 的直径 于点 ,且 是半径 OB 的中点, CD=8cm,
(1). 求直径 的长.
( 2 ). 求弓形( 阴影部分)的面积
22. (本题 10 分) 二次函数 的图象经过点(4, - 2),且对称轴为直线
( 1 )求这个二次函数的解析式.
(2)图象上的点(x, x)称为函数的不动点,求这个函数不动点的坐标.
(3)若 是二次函数图象上不动点之间的点(包括端点),求 的最大值与最小值的差.
23. (本题 10 分) 今年假期,你有没有和父母或者小伙伴一起走进影院去看一下国漫电影《哪吒 2》呀!影片中,玉虚宫的镇宫之宝 “天元鼎” 大到超乎想象,存放它的建筑是一座 “正八边形” 的宫殿,你想知道这座建筑有多大吗?
问题一:要求出 “正八边形” 的面积,我们可以把一个 “正八边形” 均分成八个顶角为_____度的等腰三角形。
问题二: 中, , , . 求 的面积和 的值分别是多少
(可以作 的中垂线 交 于 ,交 于 ,则 为等腰三角形, )
问题三:若“正八边形”的边长 为 ,求: 正八边形的面积。
24. (本题 12 分)如图,矩形 中,点 在 上, 与 相交于点 0.BE.与 相交于点 .
(1)若 平分 ,求证: 是等边三角形;
(2)找出图中一个与 相似的三角形,并说明理由;
(3)若 ,求 的长度.
(
第
1
页
)
同课章节目录
