相似三角形的判定2
图片预览

文档简介
庆云县学案 人教版初中数学九年级上册
课 题 相似三角形的判定2 课 型 新授课
单 位 庆云二中 主备人 王建峰
学习目标 掌握判定两个三角形相似的方法:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
学习重、难点 两个三角形相似的判定方法及其应用
学法指导 通过动手操作,类比归纳,合作交流得到解决问题的方法。
学 习 过 程 教师个性修订
新课引入:复习两个三角形相似的判定方法1与全等三角形判定方法(SSS)的区别与联系: 如果两个三角形的三组对应边的比相等,那么这两个三角形相似。(相似的判定方法1)回顾探究判定引例﹑判定方法1的过程探究两个三角形相似判定方法2的途径
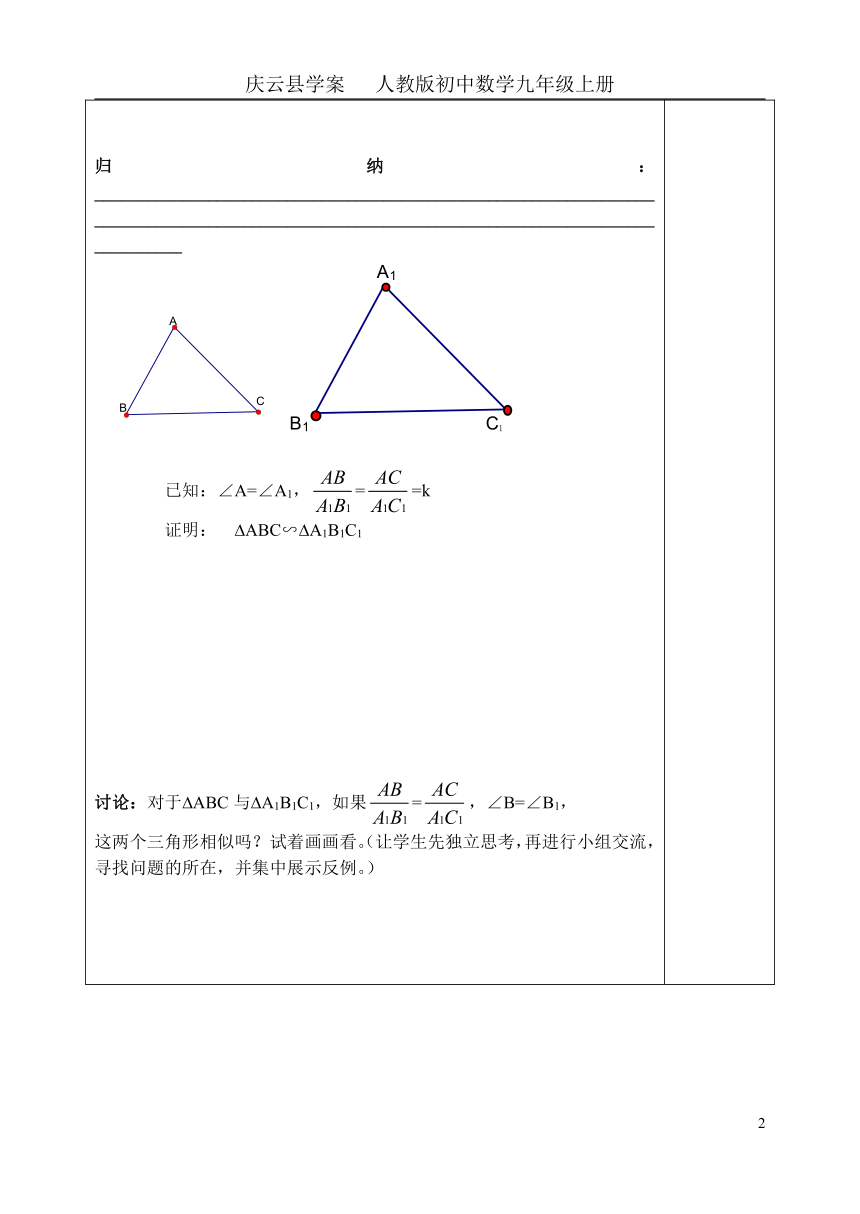
提出问题:利用刻度尺和量角器画 ABC与 A1B1C1,使∠A=∠A1,和都等于给定的值2,量出它们的第三组对应边BC和B1C1的长,它们的比等于2吗?另外两组对应角∠B与∠B1,∠C与∠C1是否相等? 如果∠A=∠A1,和都等于给定的值k呢? 延伸问题:改变∠A或k值的大小,再试一试,是否有同样的结论?(利用刻度尺和量角器,让学生先进行小组合作再作出具体判断。)归纳:__________________________________________________________________________________________________________________________________________已知:∠A=∠A1,==k证明: ABC∽ A1B1C1讨论:对于 ABC与 A1B1C1,如果=,∠B=∠B1,这两个三角形相似吗?试着画画看。(让学生先独立思考,再进行小组交流,寻找问题的所在,并集中展示反例。)
应用新知:例1:根据下列条件,判断 ABC与 A1B1C1是否相似,并说明理由:(1)∠A=1200,AB=7cm,AC=14cm, ∠A1=1200,A1B1= 3cm,A1C1=6cm。(2)∠B=1200,AB=2cm,AC=6cm, ∠B1=1200,A1B1= 8cm,A1C1=24cm。课堂练习1、(1)∠A=400,AB=8cm,AC=15cm, ∠A1=400,A1B1= 16cm,A1C1=30cm。(2)AB=10cm,BC=8cm,AC=16cm, A1B1= 16cm,B1C1=12.8cm A1C1=25.6cm。2、图中的两个三角形是否相似/3、要制作两个形状相同的三角形框架,其中一个三角形框架的三边为4、5、6,另一个的一边为2,它的另两边应是多少?你有几种答案?达标检测必做题如果△ABC∽△,AB=4,BC=7,A′B′=6,则B′C′=_______.如果△ABC∽△,∠A=∠A′=50°∠B=60°则∠C=_______。3、∠A=87°,AB=8cm,AC=7cm, ∠A′=87°, A′B′=16cm, A′C′=12cm,两个三角形相似吗?为什么?选做题已知,如图,∠A=60°,BD、CE是△ABC的两条高,求证:△ADE∽△ABC求证:相似三角形对应中线的比等于相似比。
PAGE
4
课 题 相似三角形的判定2 课 型 新授课
单 位 庆云二中 主备人 王建峰
学习目标 掌握判定两个三角形相似的方法:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
学习重、难点 两个三角形相似的判定方法及其应用
学法指导 通过动手操作,类比归纳,合作交流得到解决问题的方法。
学 习 过 程 教师个性修订
新课引入:复习两个三角形相似的判定方法1与全等三角形判定方法(SSS)的区别与联系: 如果两个三角形的三组对应边的比相等,那么这两个三角形相似。(相似的判定方法1)回顾探究判定引例﹑判定方法1的过程探究两个三角形相似判定方法2的途径
提出问题:利用刻度尺和量角器画 ABC与 A1B1C1,使∠A=∠A1,和都等于给定的值2,量出它们的第三组对应边BC和B1C1的长,它们的比等于2吗?另外两组对应角∠B与∠B1,∠C与∠C1是否相等? 如果∠A=∠A1,和都等于给定的值k呢? 延伸问题:改变∠A或k值的大小,再试一试,是否有同样的结论?(利用刻度尺和量角器,让学生先进行小组合作再作出具体判断。)归纳:__________________________________________________________________________________________________________________________________________已知:∠A=∠A1,==k证明: ABC∽ A1B1C1讨论:对于 ABC与 A1B1C1,如果=,∠B=∠B1,这两个三角形相似吗?试着画画看。(让学生先独立思考,再进行小组交流,寻找问题的所在,并集中展示反例。)
应用新知:例1:根据下列条件,判断 ABC与 A1B1C1是否相似,并说明理由:(1)∠A=1200,AB=7cm,AC=14cm, ∠A1=1200,A1B1= 3cm,A1C1=6cm。(2)∠B=1200,AB=2cm,AC=6cm, ∠B1=1200,A1B1= 8cm,A1C1=24cm。课堂练习1、(1)∠A=400,AB=8cm,AC=15cm, ∠A1=400,A1B1= 16cm,A1C1=30cm。(2)AB=10cm,BC=8cm,AC=16cm, A1B1= 16cm,B1C1=12.8cm A1C1=25.6cm。2、图中的两个三角形是否相似/3、要制作两个形状相同的三角形框架,其中一个三角形框架的三边为4、5、6,另一个的一边为2,它的另两边应是多少?你有几种答案?达标检测必做题如果△ABC∽△,AB=4,BC=7,A′B′=6,则B′C′=_______.如果△ABC∽△,∠A=∠A′=50°∠B=60°则∠C=_______。3、∠A=87°,AB=8cm,AC=7cm, ∠A′=87°, A′B′=16cm, A′C′=12cm,两个三角形相似吗?为什么?选做题已知,如图,∠A=60°,BD、CE是△ABC的两条高,求证:△ADE∽△ABC求证:相似三角形对应中线的比等于相似比。
PAGE
4
