8.3 乘法公式 课件(共26张PPT)
文档属性
| 名称 | 8.3 乘法公式 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
8.3乘法公式
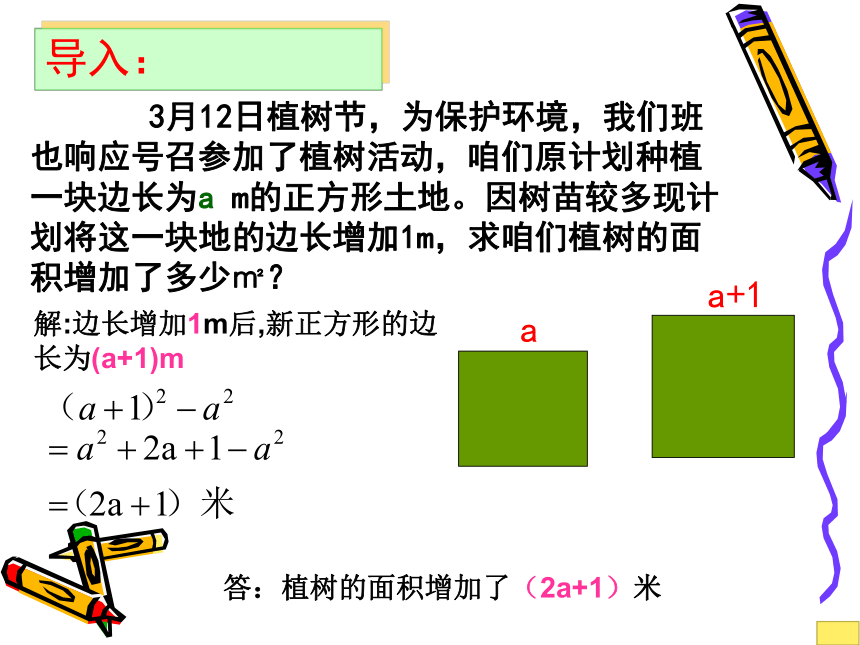
3月12日植树节,为保护环境,我们班也响应号召参加了植树活动,咱们原计划种植一块边长为a m的正方形土地。因树苗较多现计划将这一块地的边长增加1m,求咱们植树的面积增加了多少㎡?
解:边长增加1m后,新正方形的边长为(a+1)m
导入:
a
a+1
答:植树的面积增加了(2a+1)米
学习目标:
1.准确掌握平方差公式和完全平方公式及其变形公式,熟练的应用公式进行有关的运算;
2.理解两公式的几何背景,从中体验数形结合、转化、整体的数学思想方法,发展有条理的思维能力和语言表达能力;
3.通过独立思考,深入研究,合作交流养成学习的好习惯,进一步丰富数学学习的成功体验。
第一步知识回顾 环节一师友回顾
回顾平方差和完全平方公式及其变形公式
第一步知识回顾 环节二教师梳理
平方差公式
完全平方公式
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(a+b)(a-b)=a2-b2
完全平方公式变形:
教师点拨: 做题时找准公式中的a和b
填空(口答)
1、(0.2x - 3)( 0.2x + 3 )=
2、( -2x + 3y )( -2x - 3y )=
3 、(xy-2) =
4、(-m-a) =
第二步题型讲解 环节一师友讲解
例1.化简后求值:
2(a-2)(2+a)-(a+4) + 8a,其中a=-3
第二步题型讲解 环节二教师点拨
先观察能否套公式,括号前面是减号时须注意加括号!
例2:
整体思想
转化思想
换元思想
第三步互助提高 环节一师友练习
(x+y+z)(x+y-z)
第三步互助提高 环节一师友练习
(x+y+z)(x-y-z)
第三步互助提高 环节一师友练习
(x+y+z)(-x+y-z)
第三步互助提高 环节二教师提升
典型例题3:
如果x +mxy+ y =(x ± y) ,求m的值
解:因为(x ± y) =x ±2xy+y
所以 ±2
第三步互助提高 环节二教师提升
变式:
如果x +mxy+9y 为完全平方式,求m的值
第三步互助提高 环节二教师提升
变式:
如果x +(m-1)xy+9y 为完全平方式,求m的值
解题关键是找准公式中的“首”和“尾”
典型例题4:
已知:a+b=5,ab=2,求a +b 的值。
解:因为a+b=5,ab=-2
所以a +b =(a+b) -2ab
=5 -2×2
=21
所以a +b 的值是21
变式:
已知:a+b=5,a +b =11,求ab的值。
变式:
已知:a+b=5,ab=-6,求a-b的值。
教师小结:(a+b)2= a2 +b2+2ab
(a-b)2= a2 +b2-2ab
知道其中的任意两个量可以推出第三个
.
拓展提高:
(济南莱芜区期末变式)如图,两个正方形的边,长分别为a,b,且 a+b=10, ab=18,则阴影部分的面积为?
这节课我学会(懂得)了。。。
这节课我想对师傅(学友)说。。。
第四步总结提升 环节一师友归纳
本节课你的收获是什么?
知识方面:
牢牢掌握平方差公式和完全平方公式及其变形公式;
方法与思想方面:
在解题过程中要学会灵活运用公式,一题多解,并从中体验数形结合、转化、整体,换元,逆向思维的数学思想方法。
第四步总结提升 环节二教师梳理
第五步巩固反馈 环节一师友检测
选择
1.下列多项式乘法中,可以用平方差公式计算的是( )
A.(a+b)(b+a) B(-a+b)(a-b)
c.(2a+b)(b-2a) D(a -b)(b +a)
c
2.计算:
看准才行
其中x=-2,y=1
当x=-2,y=1时,原式=8
第五步巩固反馈 环节二教师寄语
评一评这节课谁表现最佳
希望在今后地学习生活中扎扎实实地走好每一步,为自己创造美好的未来!
------数学老师寄语
8.3乘法公式
3月12日植树节,为保护环境,我们班也响应号召参加了植树活动,咱们原计划种植一块边长为a m的正方形土地。因树苗较多现计划将这一块地的边长增加1m,求咱们植树的面积增加了多少㎡?
解:边长增加1m后,新正方形的边长为(a+1)m
导入:
a
a+1
答:植树的面积增加了(2a+1)米
学习目标:
1.准确掌握平方差公式和完全平方公式及其变形公式,熟练的应用公式进行有关的运算;
2.理解两公式的几何背景,从中体验数形结合、转化、整体的数学思想方法,发展有条理的思维能力和语言表达能力;
3.通过独立思考,深入研究,合作交流养成学习的好习惯,进一步丰富数学学习的成功体验。
第一步知识回顾 环节一师友回顾
回顾平方差和完全平方公式及其变形公式
第一步知识回顾 环节二教师梳理
平方差公式
完全平方公式
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(a+b)(a-b)=a2-b2
完全平方公式变形:
教师点拨: 做题时找准公式中的a和b
填空(口答)
1、(0.2x - 3)( 0.2x + 3 )=
2、( -2x + 3y )( -2x - 3y )=
3 、(xy-2) =
4、(-m-a) =
第二步题型讲解 环节一师友讲解
例1.化简后求值:
2(a-2)(2+a)-(a+4) + 8a,其中a=-3
第二步题型讲解 环节二教师点拨
先观察能否套公式,括号前面是减号时须注意加括号!
例2:
整体思想
转化思想
换元思想
第三步互助提高 环节一师友练习
(x+y+z)(x+y-z)
第三步互助提高 环节一师友练习
(x+y+z)(x-y-z)
第三步互助提高 环节一师友练习
(x+y+z)(-x+y-z)
第三步互助提高 环节二教师提升
典型例题3:
如果x +mxy+ y =(x ± y) ,求m的值
解:因为(x ± y) =x ±2xy+y
所以 ±2
第三步互助提高 环节二教师提升
变式:
如果x +mxy+9y 为完全平方式,求m的值
第三步互助提高 环节二教师提升
变式:
如果x +(m-1)xy+9y 为完全平方式,求m的值
解题关键是找准公式中的“首”和“尾”
典型例题4:
已知:a+b=5,ab=2,求a +b 的值。
解:因为a+b=5,ab=-2
所以a +b =(a+b) -2ab
=5 -2×2
=21
所以a +b 的值是21
变式:
已知:a+b=5,a +b =11,求ab的值。
变式:
已知:a+b=5,ab=-6,求a-b的值。
教师小结:(a+b)2= a2 +b2+2ab
(a-b)2= a2 +b2-2ab
知道其中的任意两个量可以推出第三个
.
拓展提高:
(济南莱芜区期末变式)如图,两个正方形的边,长分别为a,b,且 a+b=10, ab=18,则阴影部分的面积为?
这节课我学会(懂得)了。。。
这节课我想对师傅(学友)说。。。
第四步总结提升 环节一师友归纳
本节课你的收获是什么?
知识方面:
牢牢掌握平方差公式和完全平方公式及其变形公式;
方法与思想方面:
在解题过程中要学会灵活运用公式,一题多解,并从中体验数形结合、转化、整体,换元,逆向思维的数学思想方法。
第四步总结提升 环节二教师梳理
第五步巩固反馈 环节一师友检测
选择
1.下列多项式乘法中,可以用平方差公式计算的是( )
A.(a+b)(b+a) B(-a+b)(a-b)
c.(2a+b)(b-2a) D(a -b)(b +a)
c
2.计算:
看准才行
其中x=-2,y=1
当x=-2,y=1时,原式=8
第五步巩固反馈 环节二教师寄语
评一评这节课谁表现最佳
希望在今后地学习生活中扎扎实实地走好每一步,为自己创造美好的未来!
------数学老师寄语
同课章节目录
