9.2 用表达式表示变量之间的关系 课件(共21张PPT)
文档属性
| 名称 | 9.2 用表达式表示变量之间的关系 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 10:51:26 | ||
图片预览






文档简介
(共21张PPT)
9.2 用表达式表示的变量之间关系
第九章 变量之间的关系
1.能根据具体情景,用表达式表示变量间的关系,
根据表达式解决相关问题;(重点)
2.并会根据表达式求值,进一步体会自变量和因变量
的数值对应关系;(重点)
3.通过动手实践与探索,让学生参与变量的发现和
表达式的形成过程,提高分析问题和解决问题
的能力.
学习目标
我们把变化的量叫_______,其中一个叫________,另一个叫__________;________随__________的变化而变化.
变量
自变量
因变量
因变量
自变量
指出下列实例中的自变量与因变量:
(1)气温随高度变化的过程.
自变量是:________ 因变量是:________.
(2)蜡烛在燃烧的过程中,剩余蜡烛的长度随燃烧时间的变化而变化.
自变量是:________ 因变量是:__________________.
高度
气温
燃烧时间
剩余蜡烛的长度
温故复习——知识储备
支撑物高度/cm 10 20 30 40 50 60 70
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59
自变量
因变量
1.当支撑物高度为10cm时,小车下滑时间为多少?
2.当支撑物高度为50cm时,小车下滑时间为多少?
3.当支撑物高度为15cm呢?
4.23s
1.89s
用表格表示变量之间的关系
优点是直观;缺点是数据不连贯
齐心协力——新知探究
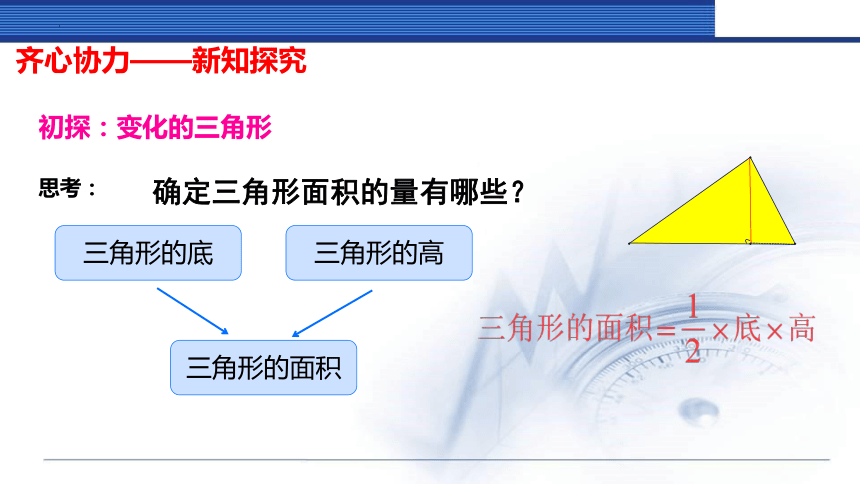
确定三角形面积的量有哪些?
初探:变化的三角形
思考:
三角形的底
三角形的高
三角形的面积
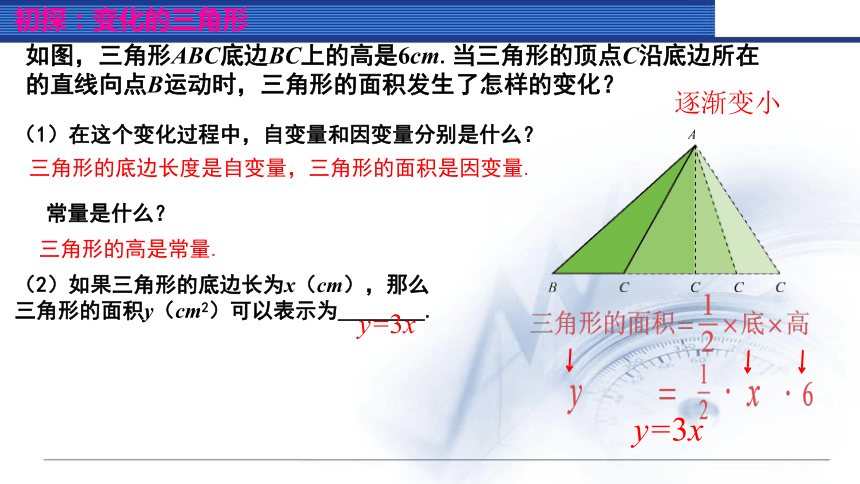
如图,三角形ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
三角形的底边长度是自变量,三角形的面积是因变量.
(1)在这个变化过程中,自变量和因变量分别是什么?
初探:变化的三角形
常量是什么?
三角形的高是常量.
逐渐变小
(2)如果三角形的底边长为x(cm),那么
三角形的面积y(cm2)可以表示为________.
y=3x
y=3x
探究中得概念
y=3x表示了 和 之间的关系
y=3x是 随 变化的表达式.
三角形面积 y
三角形底边长 x
因变量 y
自变量 x
y = 3 x
因变量
含自变量的代数式
注意:1.表达式是一个等式
2.因变量写在等号左边,含自变量的代数式写在等号右边
确定表达式的一般步骤:
三角形的底边长度是自变量x,
三角形的面积是因变量y.
1.确定变量
用字母表示变量(无字母,设字母)
y=3x
2.找等量关系
3.列表达式
化简成最简形式
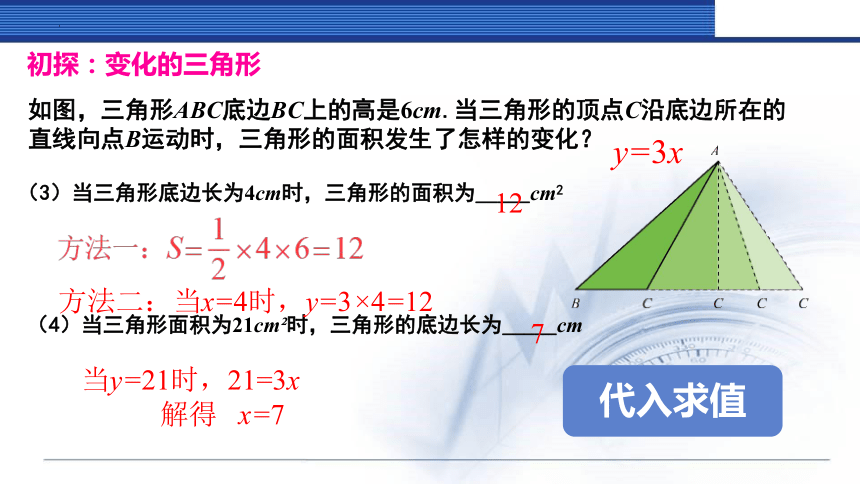
(3)当三角形底边长为4cm时,三角形的面积为_____cm2
如图,三角形ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
初探:变化的三角形
(4)当三角形面积为21cm 时,三角形的底边长为_____cm
12
7
方法二:当x=4时,y=3×4=12
当y=21时,21=3x
解得 x=7
y=3x
代入求值
(5)当底边长从12cm变化到3cm时,三角形
的面积从_____cm2变化到_____cm2.
36
9
如图,三角形ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
初探:变化的三角形
(6)当底边长增加1cm时,三角形的面积变化_____cm2.
3
数值转换机
表达式是我们表示变量之间关系的另一种方法
x(cm) ... 3 6 9 12 15 ...
y=3x(cm ) ... ...
y=3x
“输入”一个x的值就可以“输出”一个y值
表达式
表格
特点:直观
特点:可以根据任何一个自(因)变量的值求出相应的因(自)变量的值
9
18
27
36
45
y=3x
表达式
特点:可以根据任何一个自(因)变量的值求出 相应的因(自)变量的值
活动要求:1.一人任说一个自变量,找另一同学说出
对应的因变量的值;
2.一人任说一个因变量,找另一同学说出
对应的自变量的值;
1.你还记得圆锥的体积公式是什么吗?其中的字母表示什么?
2.如图,圆锥的高度是4cm,当圆锥的底面半径
由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
圆锥的底面半径的长度是自变量,圆锥的体积是因变量.
(2)如果圆锥底面半径为 r(cm),那么圆锥的
体积V(cm3)与r的表达式为________.
(3)当底面半径由1cm变化到10cm时,圆锥的体
积由 cm3变化到 cm3 .
再探:变化的圆锥
回归生活——应用模型
回归生活——应用模型
“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式.
自变量:油耗升数
因变量:开私家车的二氧化碳排放量
x
y
y=2.7x
(1)家居用电的二氧化碳排放量可以用表达式
表示为_____________,其中的字母分别表
示________________________ __.
(2)在上述关系式中,当耗电量从1 KW·h增加到100KW·h时, 二氧化碳排放量从_________增加到_________.
耗电量每增加1 KW·h,二氧化碳排放量增加___________.
0.785kg
78.5kg
0.785kg
y=0.785x
y:家居用电的二氧化碳排放量 x:耗电量
回归生活——应用模型
回归生活——应用模型
(3)小明家本月用电大约110kW·h、
天然气20m 、自来水5t、油75L,
请你计算一下小明家这几项的二
氧化碳排放总量。
小组活动要求:
四人一小组,每人负责计算一个
将结果汇总给组长进行最终的计算
课堂小结——畅谈收获
请同学们谈一谈本节课的收获
我了解了哪些知识......
我学会了什么方法......
利用所学知识能够......
总结收获——思维构建
1.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
随堂练习
C
2.(1)列车以120km/h的速度在铁路上行驶,所走路程s(km)随
行驶时间t(h)变化的表达式为 。
(2)铅笔单价0.5元,购买铅笔应付钱数y随购买支数x变化的表
达式为 。
随堂练习
3.如图,一个长方形推拉窗,窗高1.2 m,当活动窗扇沿图中所示的方向移动时,随着窗扇拉开长度b (m)的变化,窗户的通风面积A (m3)也发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)写出通风面积A与拉开长度b之间的表达式;
(3)当拉开长度b从0.2 m变化到0.4 m时,通风面积A
从_______m2变化到_______m2.
b
通风面积A与拉开长度b之间的表达式为:A=1.2b
自变量是窗扇拉开长度,因变量是窗户的通风面积.
0.24
0.48
9.2 用表达式表示的变量之间关系
第九章 变量之间的关系
1.能根据具体情景,用表达式表示变量间的关系,
根据表达式解决相关问题;(重点)
2.并会根据表达式求值,进一步体会自变量和因变量
的数值对应关系;(重点)
3.通过动手实践与探索,让学生参与变量的发现和
表达式的形成过程,提高分析问题和解决问题
的能力.
学习目标
我们把变化的量叫_______,其中一个叫________,另一个叫__________;________随__________的变化而变化.
变量
自变量
因变量
因变量
自变量
指出下列实例中的自变量与因变量:
(1)气温随高度变化的过程.
自变量是:________ 因变量是:________.
(2)蜡烛在燃烧的过程中,剩余蜡烛的长度随燃烧时间的变化而变化.
自变量是:________ 因变量是:__________________.
高度
气温
燃烧时间
剩余蜡烛的长度
温故复习——知识储备
支撑物高度/cm 10 20 30 40 50 60 70
小车下滑时间/s 4.23 3.00 2.45 2.13 1.89 1.71 1.59
自变量
因变量
1.当支撑物高度为10cm时,小车下滑时间为多少?
2.当支撑物高度为50cm时,小车下滑时间为多少?
3.当支撑物高度为15cm呢?
4.23s
1.89s
用表格表示变量之间的关系
优点是直观;缺点是数据不连贯
齐心协力——新知探究
确定三角形面积的量有哪些?
初探:变化的三角形
思考:
三角形的底
三角形的高
三角形的面积
如图,三角形ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
三角形的底边长度是自变量,三角形的面积是因变量.
(1)在这个变化过程中,自变量和因变量分别是什么?
初探:变化的三角形
常量是什么?
三角形的高是常量.
逐渐变小
(2)如果三角形的底边长为x(cm),那么
三角形的面积y(cm2)可以表示为________.
y=3x
y=3x
探究中得概念
y=3x表示了 和 之间的关系
y=3x是 随 变化的表达式.
三角形面积 y
三角形底边长 x
因变量 y
自变量 x
y = 3 x
因变量
含自变量的代数式
注意:1.表达式是一个等式
2.因变量写在等号左边,含自变量的代数式写在等号右边
确定表达式的一般步骤:
三角形的底边长度是自变量x,
三角形的面积是因变量y.
1.确定变量
用字母表示变量(无字母,设字母)
y=3x
2.找等量关系
3.列表达式
化简成最简形式
(3)当三角形底边长为4cm时,三角形的面积为_____cm2
如图,三角形ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
初探:变化的三角形
(4)当三角形面积为21cm 时,三角形的底边长为_____cm
12
7
方法二:当x=4时,y=3×4=12
当y=21时,21=3x
解得 x=7
y=3x
代入求值
(5)当底边长从12cm变化到3cm时,三角形
的面积从_____cm2变化到_____cm2.
36
9
如图,三角形ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
初探:变化的三角形
(6)当底边长增加1cm时,三角形的面积变化_____cm2.
3
数值转换机
表达式是我们表示变量之间关系的另一种方法
x(cm) ... 3 6 9 12 15 ...
y=3x(cm ) ... ...
y=3x
“输入”一个x的值就可以“输出”一个y值
表达式
表格
特点:直观
特点:可以根据任何一个自(因)变量的值求出相应的因(自)变量的值
9
18
27
36
45
y=3x
表达式
特点:可以根据任何一个自(因)变量的值求出 相应的因(自)变量的值
活动要求:1.一人任说一个自变量,找另一同学说出
对应的因变量的值;
2.一人任说一个因变量,找另一同学说出
对应的自变量的值;
1.你还记得圆锥的体积公式是什么吗?其中的字母表示什么?
2.如图,圆锥的高度是4cm,当圆锥的底面半径
由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
圆锥的底面半径的长度是自变量,圆锥的体积是因变量.
(2)如果圆锥底面半径为 r(cm),那么圆锥的
体积V(cm3)与r的表达式为________.
(3)当底面半径由1cm变化到10cm时,圆锥的体
积由 cm3变化到 cm3 .
再探:变化的圆锥
回归生活——应用模型
回归生活——应用模型
“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式.
自变量:油耗升数
因变量:开私家车的二氧化碳排放量
x
y
y=2.7x
(1)家居用电的二氧化碳排放量可以用表达式
表示为_____________,其中的字母分别表
示________________________ __.
(2)在上述关系式中,当耗电量从1 KW·h增加到100KW·h时, 二氧化碳排放量从_________增加到_________.
耗电量每增加1 KW·h,二氧化碳排放量增加___________.
0.785kg
78.5kg
0.785kg
y=0.785x
y:家居用电的二氧化碳排放量 x:耗电量
回归生活——应用模型
回归生活——应用模型
(3)小明家本月用电大约110kW·h、
天然气20m 、自来水5t、油75L,
请你计算一下小明家这几项的二
氧化碳排放总量。
小组活动要求:
四人一小组,每人负责计算一个
将结果汇总给组长进行最终的计算
课堂小结——畅谈收获
请同学们谈一谈本节课的收获
我了解了哪些知识......
我学会了什么方法......
利用所学知识能够......
总结收获——思维构建
1.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
随堂练习
C
2.(1)列车以120km/h的速度在铁路上行驶,所走路程s(km)随
行驶时间t(h)变化的表达式为 。
(2)铅笔单价0.5元,购买铅笔应付钱数y随购买支数x变化的表
达式为 。
随堂练习
3.如图,一个长方形推拉窗,窗高1.2 m,当活动窗扇沿图中所示的方向移动时,随着窗扇拉开长度b (m)的变化,窗户的通风面积A (m3)也发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)写出通风面积A与拉开长度b之间的表达式;
(3)当拉开长度b从0.2 m变化到0.4 m时,通风面积A
从_______m2变化到_______m2.
b
通风面积A与拉开长度b之间的表达式为:A=1.2b
自变量是窗扇拉开长度,因变量是窗户的通风面积.
0.24
0.48
同课章节目录
