2025年九年级中考数学三轮冲刺练习四边形中的相似三角形压轴题练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习四边形中的相似三角形压轴题练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1016.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 10:13:09 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习四边形中的相似三角形压轴题练习
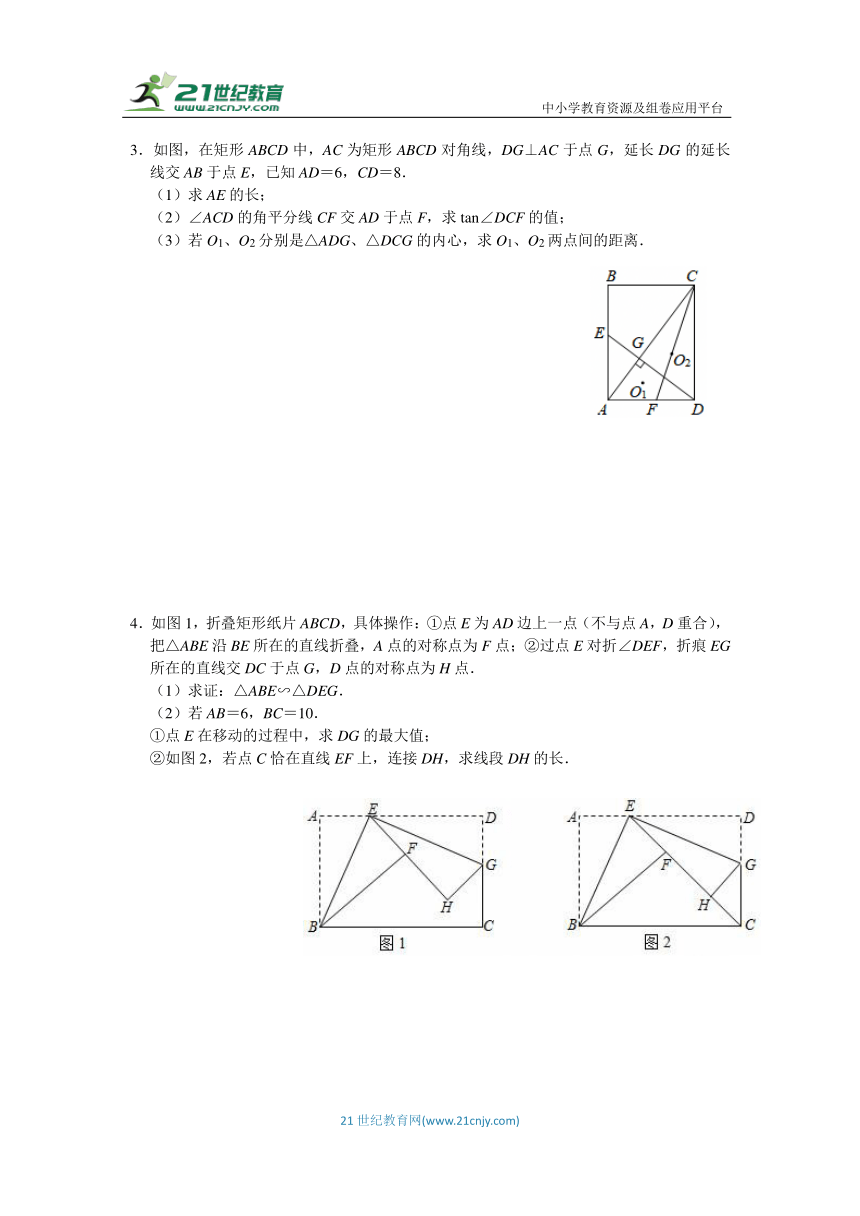
1.如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60°,OM=4,OQ=1,求CP的长;(提示:过点P作PE⊥OA)
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形,
①证明:是定值;
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求的取值范围.
2.如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
(1)求证:AG=CG;
(2)求证:△AEG∽△FAG;
(3)若GE GF=9,求AG的长.
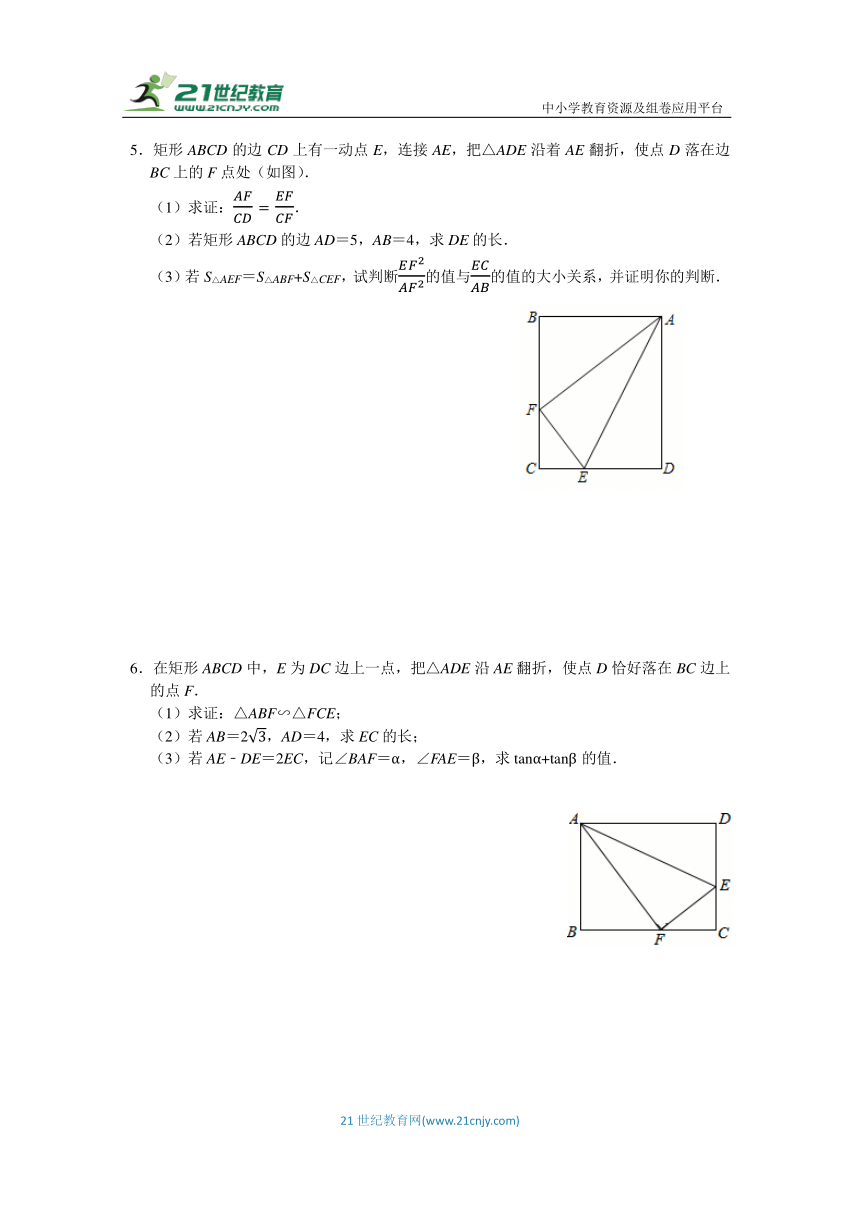
3.如图,在矩形ABCD中,AC为矩形ABCD对角线,DG⊥AC于点G,延长DG的延长线交AB于点E,已知AD=6,CD=8.
(1)求AE的长;
(2)∠ACD的角平分线CF交AD于点F,求tan∠DCF的值;
(3)若O1、O2分别是△ADG、△DCG的内心,求O1、O2两点间的距离.
4.如图1,折叠矩形纸片ABCD,具体操作:①点E为AD边上一点(不与点A,D重合),把△ABE沿BE所在的直线折叠,A点的对称点为F点;②过点E对折∠DEF,折痕EG所在的直线交DC于点G,D点的对称点为H点.
(1)求证:△ABE∽△DEG.
(2)若AB=6,BC=10.
①点E在移动的过程中,求DG的最大值;
②如图2,若点C恰在直线EF上,连接DH,求线段DH的长.
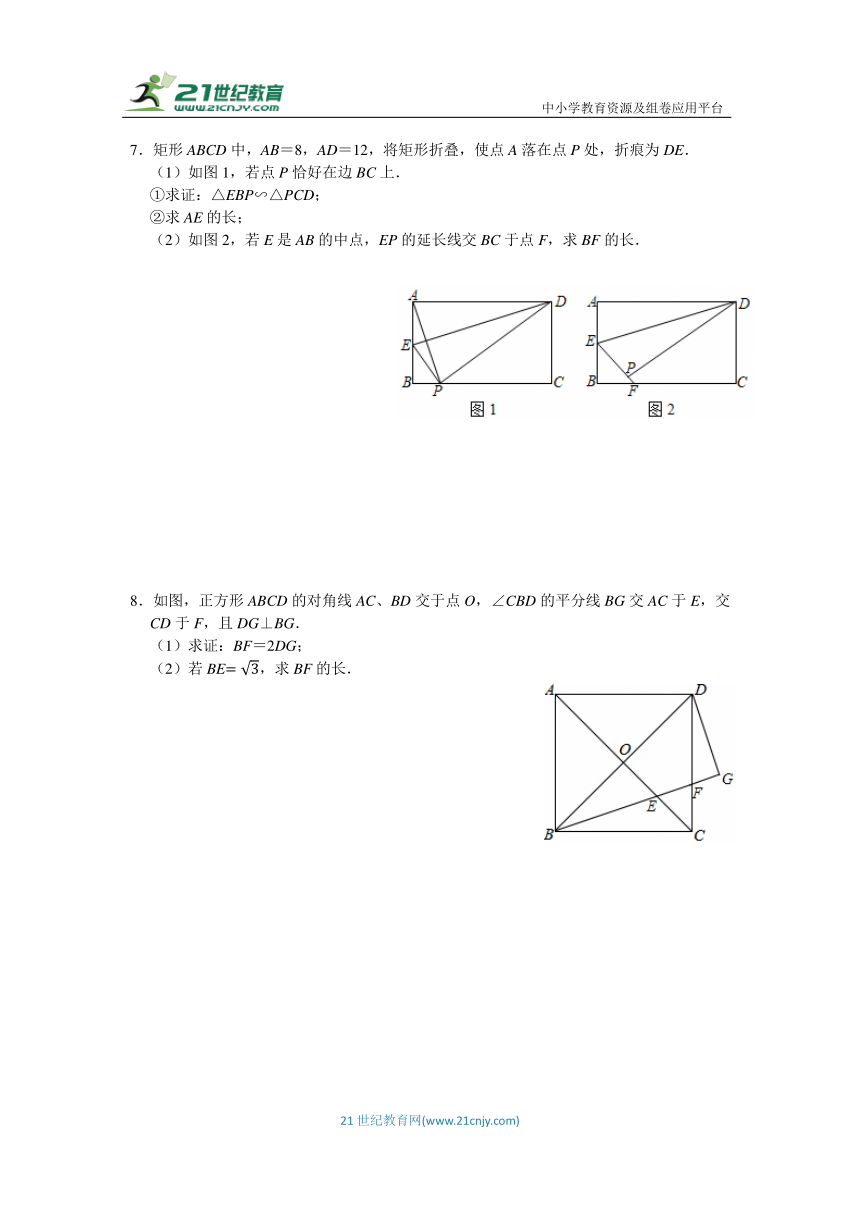
5.矩形ABCD的边CD上有一动点E,连接AE,把△ADE沿着AE翻折,使点D落在边BC上的F点处(如图).
(1)求证:.
(2)若矩形ABCD的边AD=5,AB=4,求DE的长.
(3)若S△AEF=S△ABF+S△CEF,试判断的值与的值的大小关系,并证明你的判断.
6.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=2,AD=4,求EC的长;
(3)若AE﹣DE=2EC,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.
7.矩形ABCD中,AB=8,AD=12,将矩形折叠,使点A落在点P处,折痕为DE.
(1)如图1,若点P恰好在边BC上.
①求证:△EBP∽△PCD;
②求AE的长;
(2)如图2,若E是AB的中点,EP的延长线交BC于点F,求BF的长.
8.如图,正方形ABCD的对角线AC、BD交于点O,∠CBD的平分线BG交AC于E,交CD于F,且DG⊥BG.
(1)求证:BF=2DG;
(2)若BE,求BF的长.
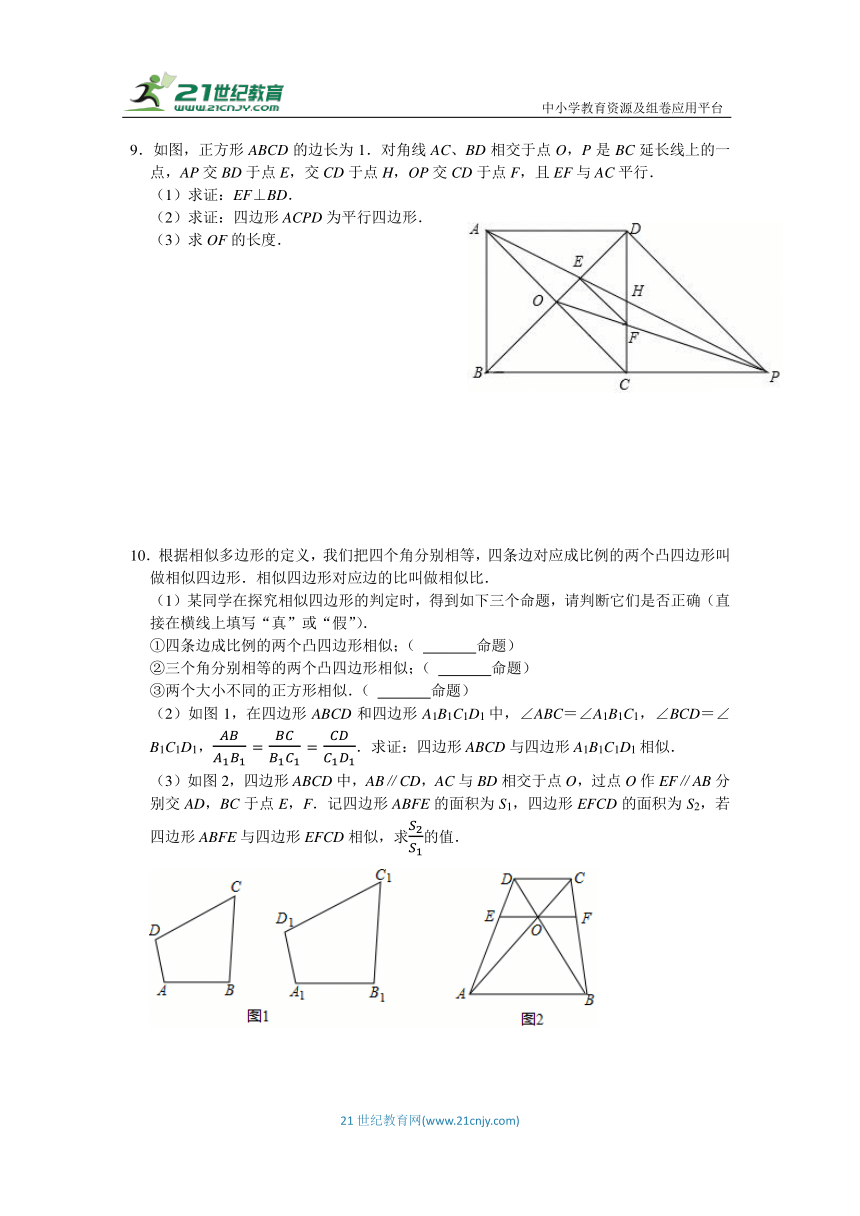
9.如图,正方形ABCD的边长为1.对角线AC、BD相交于点O,P是BC延长线上的一点,AP交BD于点E,交CD于点H,OP交CD于点F,且EF与AC平行.
(1)求证:EF⊥BD.
(2)求证:四边形ACPD为平行四边形.
(3)求OF的长度.
10.根据相似多边形的定义,我们把四个角分别相等,四条边对应成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图1,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
(3)如图2,四边形ABCD中,AB∥CD,AC与BD相交于点O,过点O作EF∥AB分别交AD,BC于点E,F.记四边形ABFE的面积为S1,四边形EFCD的面积为S2,若四边形ABFE与四边形EFCD相似,求的值.
11.如图,平行四边形ABCD中,点P为CB延长线上点,连接DP交AC于点M、交AB于点N,已知DA=DC,∠ACD=45°.
(1)求证:四边形ABCD为正方形;
(2)连接BM,若N为AB的中点,求tan∠BMP的值;
(3)若MN=2,PN=6,求DM的长.
12.如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G.
(1)求四边形OEBF的面积;
(2)求证:OG BD=EF2;
(3)在旋转过程中,当△BEF与△COF的面积之和最大时,求AE的长.
13.如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,G在BC上移动,P是线段DF的中点,连接PG,PC.
(1)求∠DBF的大小;
(2)证明:DB∥PG;
(3)若∠BEF=60°,求PG:PC的值.
14.已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE;过点E作EG⊥AD交AC于点G.
(1)求证:四边形AFCE是菱形;
(2)求证:2AF2=AC AG;
(3)若AE=a,在△ABF中,AB>BF,△ABF的面积为b,且b,求tan∠OEG.
15.在 ABCD中,AC为对角线,点G在AB的延长线上,连接CG,点F在CG上,线段AF交BC于点E,若FA=FC,如图1.
(1)已知∠CAD=∠G,求证:AC2=CE BC;
(2)如图2,已知AF⊥BC,垂足为点E.
①若∠GCB=∠DAC,求证:AE=FE;
②若,AD=4,tan∠ABC=2,求BG的长.
16.在矩形ABCD中,点E在AB边上,CE=CD,过点B作BF∥CE交DE的延长线于点F,连接AF.
(1)如图1,求证:△AFB≌△CBE;
(2)如图2,连接BD交CE于点G,若CG=BF.
(i)求证:AF∥DG;
(ii)求的值.
17.如图,在菱形ABCD中,AB=6,∠B=60°,点E,F分别是AB,AD上的动点,满足AE=DF,连接CE,CF,EF,EF与AC交于点G.
(1)求∠ECF的度数;
(2)填空:
① ,
② ,
③ ;
(3)记△AEG的面积为S1,△AFG的面积为S2,△AEC的面积为S3,△AFC的面积为S4.
①若CF2=3AF FD,求的值;
②试判断的值是否存在最小值?若存在,求出这个值;若不存在,请说明理由.
18.在四边形ABCD中,点E为AB的中点,分别连接CE,DE.
(1)如图1,若∠A=∠B,∠ADE=∠BEC.
(i)求证:AE2=AD BC;
(ii)求证:DE平分∠ADC;
(2)如图2,若∠DAB+∠B=90°,∠DEC=90°,AD=3,BC=1,求CD的长.
19.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如1,在正方形ABCD中,E,F分别是AB、AD上两点,连接DE,CF,若AE=DF,求证:△AED≌△DFC;
(2)在(1)的条件下,求证:DE⊥CF;
(3)如图2,在矩形ABCD中,过点C作CE⊥BD交AD于点E,若,求的值;
(4)如图3,在四边形ABCD中,∠A=∠B=90°,E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于F,且AB=5,AD=3,CF=6,求DE的长.
参考答案
1.【解答】解:(1)如图1,过点P作PE⊥OA于点E.
∵PQ∥OA,PM∥OB,
∴四边形OMPQ为平行四边形,
∴PM=OQ=1,∠PME=∠AOB=60°,
∴PE=PM sin60°,ME,
∴CE=OC﹣OM﹣ME,
由勾股定理得;
(2)①证明:设OM=x,ON=y,
∵四边形OMPQ为菱形,
∴OQ=QP=OM=x,NQ=y﹣x,
∵PQ∥OA,
∴△NQP∽△NOC,
∴,
即,
∴6y﹣6x=xy,两边都除以6xy,得,
即;
②如图2,过点P作PE⊥OA于点E,过点N作NF⊥OA于点F,
则S1=OM PE,S2OC NF,
∴,
∵PM∥OB,
∴△CPM∽△CNO.
∴,
∴,
∵0<x<6,
∴.
2.【解答】(1)证明:∵BD是正方形ABCD的对角线,
∴∠ADB=∠CDB=45°,
∵四边形ABCD是正方形,
∴AD=CD,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴AG=CG;
(2)证明:∵四边形ABCD是正方形,
∴AD∥CB,
∴∠FCB=∠F,
由(1)可知△ADG≌△CDG,
∴∠DAG=∠DCG,
∴∠DAB﹣∠DAG=∠DCB﹣∠DCG,即∠BCF=∠BAG,
∴∠EAG=∠F,
又∠EGA=∠AGF,
∴△AEG∽△FAG;
(3)解:由(2)得△AEG∽△FAG,
∴,即GA2=GE GF=9,
∴GA=3或GA=﹣3(舍去),
故AG的长为3.
3.【解答】解:(1)∵四边形ABCD是矩形,
∴∠B=BAD=90°,AB=CD=8,AD=BC=6,
∴∠DAG+∠BAC=90°,
∵DG⊥AC,
∴∠DAG+∠ADE=90°,
∴∠BAC=∠ADE,
∴tan∠BAC=tan∠ADE,
∴,即:,
∴AE;
(2)如图1,过点F作FH⊥AC于点H,
∵CF平分∠ACD,FD⊥CD,FH⊥CA,
∴FD=FH,
∵∠ADC=90°,
∴AC10,
∵S△ACF+S△DCF=S△ACD,
∴AC FHCD FDAD CD,
∴10×FD8×FD6×8,
∴FD,
∴tan∠DCF;
(3)过点O1作O1N⊥AC于点N,过点O2作O2M⊥AC于点M,作O1K⊥O2M于点K,
则∠O1NMK是矩形,
∵DG AC=AD CD,
∴DG,
∴AG=DG tan∠ADE=DG,
∴CG=AC﹣AG=10,
∵O1、O2分别是Rt△ADG、Rt△DCG的内心,设⊙O1的半径为r1,⊙O2的半径为r2,
∴r1,r2,
∴O1K=MN=r1+r2,O2K=r2﹣r1,
∵∠O1KO2=90°,
∴O1O22.
4.【解答】解:(1)如图1中,
由折叠可知,∠AEB=∠FEB,∠DEG=∠HEG,
∵∠AEB+∠FEB+∠DEG+∠HEG=180°,
∴∠AEB+∠DEG=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=∠AEB+∠ABE=90°,
∴∠ABE=∠DEG,
∴△ABE∽△DEG.
(2)①设AE=x,
∵△ABE∽△DEG,
∴,
∴,
∴DG(x﹣5)2,
∵0(0<x<10),
∴x=5时,DG有最大值,最大值为.
②如图2中,连接DH.
由折叠可知∠AEB=∠FEB,AE=EF,AB=BF=6,∠BFE=∠A=90°,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠FEB=∠EBC,
∴CE=CB=10,
∵点C在直线EF上,
∴∠BFC=90°,CF=10﹣EF=10﹣AE,
∴CF8,
∴AE=EF=CE﹣CF=10﹣8=2,
∴DG,
∴EG,
由折叠可知,EG垂直平分线段DH,
∴DH=22.
5.【解答】(1)证明:∵△ADE沿着AE翻折,使点D落在边BC上的F点处,
∴△AED≌△AFE,
∴∠CFE+∠BFA=90°,
∴∠AFE=∠D=90°,
在矩形ABCD中,∠B=∠C=90°,
∴∠BFA+∠BAF=90°,
∴∠CFE=∠BAF,
∴△ABF∽△FCE,
∴,
∵AB=CD,
∴;
(2)解:设ED=x,
∵CD=AB=4,
∴CE=4﹣x,FE=x,
又∵AF=AD=5,AB2+BF2=AF2,
∴BF3,
∴CF=5﹣3=2,
∵CF2+CE2=EF2,
∴22+(4﹣x)2=x2,
∴x,
∴DE;
(3)答:相等.
证明:∵S△AEF=S△ABF+S△EFC,
∴S△AEF,
过F作AB的平行线交AE于G,则(AB+CE)BC,
∴FG(AB+CE),
过E作EH⊥AB于H,交FG于M.
∵FG∥AB∥CE,
∴FM(BH+CE),
∴FM+GM(BH+AH+CE),
∴GMAH,
∴G,F分别为AE、BC中点.
在Rt△ABF中,BFBCAF.
∴∠BAF=30°,
∴∠BAF=∠CFE=∠EAF=30°,
∵∠ABF=∠AFE=∠FCE=90°,
∴△ABF∽△AEF,△AFE∽△FCE,
∴,,
∴AF2=AE AB,EF2=AE CE,
∴,
∴.
6.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
由翻折可知,∠D=∠AFE=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠CEF=90°,
∴∠AFB=∠FEC,
∴△ABF∽△FCE.
(2)设EC=x,
由翻折可知,AD=AF=4,
∴BF2,
∴CF=BC﹣BF=2,
∵△ABF∽△FCE,
∴,
∴,
∴x,
∴EC.
(3)∵△ABF∽△FCE,
∴,
∴tanα+tanβ,
设AB=CD=a,BC=AD=b,DE=x,
∴AE=DE+2CE=x+2(a﹣x)=2a﹣x,
∵AD=AF=b,DE=EF=x,∠B=∠C=∠D=90°,
∴BF,CF,
∵AD2+DE2=AE2,
∴b2+x2=(2a﹣x)2,
∴a2﹣axb2,
∵△ABF∽△FCE,
∴,
∴,
∴a2﹣ax ,
∴b2 ,
整理得,16a4﹣24a2b2+9b4=0,
∴(4a2﹣3b2)2=0,
∴,
∴tanα+tanβ.
7.【解答】解:(1)①∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,
∴∠BPE+∠BEP=90°,
由折叠知,∠DPE=∠BAD=90°,
∴∠BPE+∠CPD=90°,
∴∠BEP=∠CPD,
∵∠B=∠C=90°,
∴△EBP∽△PCD;
②∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=8,BC=AD=12,
由折叠知,PE=AE,DP=AD=12,
在Rt△DPC中,CP4,
∴BP=BC﹣CP=12﹣4,
在Rt△PBE中,PE2﹣BE2=BP2,
∴AE2﹣(8﹣AE)2=(12﹣4)2,
∴AE=18﹣6;
(2)如图,过点P作GH∥BC交AB于G,交CD于H.
则四边形AGHD是矩形,
设EG=x,则BG=4﹣x,
∵∠A=∠EPD=90°,∠EGP=∠DHP=90°,
∴∠EPG+∠DPH=90°,∠DPH+∠PDH=90°,
∴∠EPG=∠PDH,
∴△EGP∽△PHD,
∴,
∴PH=3EG=3x,DH=AG=4+x,
在Rt△PHD中,PH2+DH2=PD2,
∴(3x)2+(4+x)2=122,
解得x(负值已经舍弃),
∴BG=4,
在Rt△EGP中,GP,
∵GH∥BC,
∴△EGP∽△EBF,
∴,
∴,
∴BF=3.
8.【解答】(1)证明:延长DG、BC交于点H,
∵BG平分∠CBD,
∴∠1=∠2,
∵DG⊥BG,
∴∠BGD=∠BGH=90°,
又∵BG=BG,
∴△BGD≌△BGH(ASA),
∴BD=BH,
∴DH=2DG,
∵四边形ABCD是正方形,
∴BC=DC,∠BCF=∠DCH=90°,
又∵∠BGD=90°,∠3=∠4,
∴∠2=∠5,
∴△BCF≌△DCH(ASA),
∴BF=DH,
∴BF=2DG;
(2)∵四边形ABCD是正方形,
∴∠ACB=∠BDC=45°,
∴∠BCE=∠BDF,
又∵∠1=∠2,
∴△BEC∽△BFD,
∴,
∵BE,
∴BF.
9.【解答】(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∵EF∥AC,
∴EF⊥BD;
(2)证明:
∵EF∥AC,
∴,,
∵四边形ABCD是正方形,
∴AD∥CP,OA=OC,
∴,
即,
∴AO∥DP,
∵AD∥CP,
∴四边形ACPD为平行四边形;
(3)解:由勾股定理得:AC=BD,
∵四边形ACPD为平行四边形,
∴CP=AD=BC,
∴,
∵AD∥BP,
∴,
∴DEBD,OE=OD﹣DE,
∵DOBD,
∵∠DEF=∠DOC=90°﹣∠EDF=45°,
∴∠DFE=45°,
∴EF=DE,
在Rt△OEF中,由勾股定理得:OF.
10.【解答】(1)解:①四条边成比例的两个凸四边形相似,是假命题,角不一定相等.
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例.
③两个大小不同的正方形相似.是真命题.
故答案为假,假,真.
(2)证明:如图1中,连接BD,B1D1.
∵∠BCD=∠B1C1D1,且,
∴△BCD∽△B1C1D1,
∴∠CDB=∠C1D1B1,∠C1B1D1=∠CBD,
∵,
∴,
∵∠ABC=∠A1B1C1,
∴∠ABD=∠A1B1D1,
∴△ABD∽△A1B1D1,
∴,∠A=∠A1,∠ADB=∠A1D1B1,
∴,∠ADC=∠A1D1C1,∠A=∠A1,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,
∴四边形ABCD与四边形A1B1C1D1相似.
(3)如图2中,
∵四边形ABFE与四边形EFCD相似.
∴,
∵EF=OE+OF,
∴,
∵EF∥AB∥CD,
∴,,
∴,
∴,
∵AD=DE+AE,
∴,
∴2AE=DE+AE,
∴AE=DE,
∴四边形ABFE与四边形EFCD相似比为1
∴1.
11.【解答】(1)证明:∵四边形ABCD是平行四边形,DA=DC,
∴四边形ABCD是菱形,
∵DA=DC,
∴∠ACD=∠CAD=45°,
∴∠ADC=90°,
∴四边形ABCD为正方形;
(2)解:作BE⊥PD,如图所示:
则∠PEB=∠MEB=90°,
设正方形ABCD的边长为a,
∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AB=AD=a,∠PBN=∠DAB=∠BCD=90°,
∵N为AB的中点,
∴AN=BNABa,
在△BPN和△ADN中,,
∴△BPN≌△ADN(ASA),
∴BP=AD=a,PN=DNa,PC=BP+BC=2a,
∴PD=2DNa,
∵AD∥BC,
∴△ADM∽△CPM,
∴,
∴PMPDa,
∵∠PEB=∠PCD=90°,∠P=∠P,
∴△PBE∽△PDC,
∴,即,
解得:BEa,PEa,
∴EM=PM﹣PEa,
∴tan∠BMP;
(3)解:MN=2,PN=6,
∴MP=8,
∵AB∥CD,
∴AM:MC=MN:MD,
∵AD∥BC,
∴AM:MC=DM:MP,
∴MN:MD=DM:MP,
∴MD2=MN MP=2×8=16,
∴MD=4.
12.【解答】解:(1)∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOCS正方形ABCD1×1;
(2)证明:∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OG OB=OE2,
∵OBBD,OEEF,
∴OG BD=EF2;
(3)如图,过点O作OH⊥BC,
∵BC=1,
∴OHBC,
设AE=x,则BE=CF=1﹣x,BF=x,
∴S△BEF+S△COFBE BFCF OHx(1﹣x)(1﹣x)(x)2,
∵a0,
∴当x时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE.
13.【解答】解:(1)在菱形ABCD和菱形BEFG中,
∵∠DBC∠ABC,∠FBG∠EBG,
∵∠ABC+∠EBG=180°,
∴∠DBF=∠DBC+∠FBG=90°;
(2)如图,
延长GP交DC于点H,
∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP(ASA),
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH,
∴1,
∵∠HCG=∠DCB,
∴△CHG∽△CDB,
∴∠CGP=∠CBD,
∴DB∥PG;
(3)∵CG=CH,
∴△CHG是等腰三角形,
∴PG⊥PC,(三线合一)
又∵∠ABC=∠BEF=60°,
∴∠GCPBCD=60°,
∴.
14.【解答】(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AFCE是菱形.
(2)证明:∵EG⊥AD
∴∠AEG=90°,
∵∠AOE=90°,
∴∠AEG=∠AOE,
∵∠EAO=∠EAG,
∴△AOE∽△AEG,
∴,
∴AE2=AO AG,即2AF2=AC AG;
(3)解:∵四边形AFCE是菱形,
∴AF=AE=a,
在Rt△ABF中,AB2+BF2=AF2,
∴AB2+BF2=a2,
∴(AB+BF)2﹣2AB BF=a2①,
∵△ABF的面积为b,
∴AB BF=b,
∴AB BF=2b②,
由①、②得:(AB+BF)2=a2+4b,
∵AB+BF>0,
∴AB+BFa,
设DE=x,则CD=(a﹣x),则
x(a﹣x)=b,
解得x1a,x2a(舍去),
∴CDa,
∵∠EAG+∠EGA=∠OEG+∠EGA=90°,
∴∠EAG=∠OEG,
∴tan∠OEG=tan∠EAG.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠ABC=∠D,AD∥BC,
∴∠CAD=∠ACB,
∵∠CAD=∠G,
∴∠ACB=∠G,
∵∠ABC=∠G+∠BCG,∠ACG=∠ACB+∠BCG,
∴∠ABC=∠ACG,
∵FA=FC,
∴∠CAF=∠ACG,
∴∠ABC=∠CAF,
∵∠ACB=∠ECA,
∴△ACB∽△ECA,
∴,
∴AC2=CE BC;
(2)①证明:∵∠GCB=∠DAC,由(1)得∠CAD=∠ACB,
∴∠GCB=∠ACB,
∵AF⊥BC,
∴∠FEC=∠AEC=90°,
∵CE=CE,
∴△FEC≌△AEC(ASA),
∴AE=FE;
②解:过点F作 FH⊥AC于点H,延长AD与GC的延长线交于点K,如下图所示:
∵四边形ABCD为平行四边形,
∴,BC=AD=4,AB∥CD,BC∥AD,
又∵AE⊥BC,在Rt△ABE中,,
∴AE=2BE,
由勾股定理得AE2+BE2=AB2,
即,
∴BE=1,
∴AE=2BE=2,
∴CE=BC﹣BE=3,
在Rt△ACE中,由勾股定理得,
∵FA=FC,FH⊥AC,
∴,
∵,
∴,
在Rt△AFH中,由勾股定理得AF2﹣FH2=AH2,
即()2,
∴AF(负值舍去),
∴FE=AF﹣AE,
∵CE∥AK,
∴△CEF∽△KAF,
∴,
∴,
∴AK,
∵CD∥AG,
∴△KDC∽△KAG,
∴,
∴,
∴AG,
∴BG=AG﹣AB.
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠CDE=∠BEF,
∵BF∥CE,
∴∠CED=∠BFE,∠ABF=∠CEB,
∵CE=CD,
∴∠CDE=∠CED,AB=CE,
∴∠BEF=∠BFE,
∴BF=BE,
在△AFB和△CBE中,
,
∴△AFB≌△CBE(SAS);
(2)(i)证明:连接GF,如图2,
∵CG=BF,CG∥BF,
∴四边形BCGF为平行四边形,
∴GF=BC,GF∥BC,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴AD=GF,AD∥GF,
∴四边形ADGF为平行四边形,
∴AF∥DG;
(ii)解:∵BF=BE,CG=BF,
∴CG=BF=BE,
∵AB=CE,
∴EG=AE,
设CG=BF=BE=y,EG=AE=x,则AB=x+y,
∵AF∥DG,
∴∠BAF=∠EBG,
又∵∠ABF=∠BEG,
∴△ABF∽△BEG,
∴,
即,
解得,
又∵AF∥DB,
∴△AFE∽△BDE,
∴.
17.【解答】解:(1)在菱形ABCD中,∵AB=BC=CD=AD,且∠B=∠D=60°
∴△ABC,△ADC都是等边三角形,
∴AC=CD,∠CAE=60°=∠D=∠ACD.
∵AE=DF,
∴△AEC≌△DFC(SAS),
∴∠ACE=∠DCF,
∴∠ECF=60°;
(2)由(1)△ABC,△ADC都是等边三角形,
∴AB=AC=AD,
∵AE=DE,
∴①1,
②由(1)知△AEC≌△DFC,
∴CE=CF,
∵∠ECF=60°,
∴△CEF是等边三角形,
∴∠CFE=60°=∠CAF,
∵∠FCG=∠ACF,
∴△CFG∽△CAF,
∴,
∴,
∵AC=CD,CF=CE,
∴,
∴0;
③∵∠EAG=∠CFG=60°,∠AGE=∠CGF,
∴△AGE∽△FGC,
∴,
同理,,
∴1,
故答案为:1,0,1;
(3)①由△AGF∽△DFC可得,
即AF DF=AG CD=AG AC,
由△CGF∽△CFA可得,
即CF2=AC CG
∵CF=3AF FD,
∴CG=3AG,
∴AC=4AG,
∴;
②由(2)知△AEG∽△FCG,
∴∠AEG=∠FCG,
∵∠EAG=∠CAF=60°,
∴△AGE∽△AFC,
同理△AGF∽△AEC,
∴.
设AE=DF=x,
则,
当x=3时,的值最小,最小值为.
18.【解答】(1)证明:(i)∠A=∠B,∠ADE=∠BEC,
∴△AED∽△BCE,
∴,
∵E为AB的中点,
∴AE=BE,
∴,
即AE2=AD BC;
(ii)∵∠AED+∠DEC+∠CEB=180°,∠AED+∠ADE+∠A=180°,
∴∠A+∠ADE=∠DEC+∠CEB,
∵∠ADE=∠BEC,
∴∠A=∠DEC,
∵∠A=∠B,∠ADE=∠BEC,
∴△AED∽△BCE,
∴,
∵AE=BE,
∴,
∴△ADE∽△EDC,
∴∠ADE=∠EDC,
∴DE平分∠ADC;
(2)解:如图,过点A作AF∥BC,交CE的延长线于点F,连接DF,
∴∠FAE=∠B,
∵AE=BE,∠AEF=∠BEC,
∴△AEF≌△BEC(ASA),
∴AF=BC,EF=EC,
∵∠DAB+∠B=90°,
∴∠DAB+∠BAF=90°,
∴∠DAF=90°.
∵∠DEC=90°,
∴DF=DC,
在Rt△ADF中,AD2+AF2=DF2,
∵AD=3,BC=1,
∴AF=1,
∴CD=DF.
19.【解答】(1)证明:由正方形可知∠A=∠FDC=90°,AD=CD,
在△AED与△DFC中,
,
∴△AED≌△DFC(SAS);
(2)证明:由正方形性质可知∠ADE+∠AED=90°,
∵△AED≌△DFC(AAS),
∴∠DFC=∠AED,
∴∠DFC+∠ADE=90°,
∴DE⊥CF;
(3)解:如图2,设BD与CE交于点G,
由条件可知∠A=∠EDC=90°,AB=CD,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
∵,
∴;
(4)解:如图3,过点C作CH⊥AF交AF的延长线于点H,
由条件可知∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴,
∴.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习四边形中的相似三角形压轴题练习
1.如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60°,OM=4,OQ=1,求CP的长;(提示:过点P作PE⊥OA)
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形,
①证明:是定值;
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求的取值范围.
2.如图,在正方形ABCD中,点G是对角线上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
(1)求证:AG=CG;
(2)求证:△AEG∽△FAG;
(3)若GE GF=9,求AG的长.
3.如图,在矩形ABCD中,AC为矩形ABCD对角线,DG⊥AC于点G,延长DG的延长线交AB于点E,已知AD=6,CD=8.
(1)求AE的长;
(2)∠ACD的角平分线CF交AD于点F,求tan∠DCF的值;
(3)若O1、O2分别是△ADG、△DCG的内心,求O1、O2两点间的距离.
4.如图1,折叠矩形纸片ABCD,具体操作:①点E为AD边上一点(不与点A,D重合),把△ABE沿BE所在的直线折叠,A点的对称点为F点;②过点E对折∠DEF,折痕EG所在的直线交DC于点G,D点的对称点为H点.
(1)求证:△ABE∽△DEG.
(2)若AB=6,BC=10.
①点E在移动的过程中,求DG的最大值;
②如图2,若点C恰在直线EF上,连接DH,求线段DH的长.
5.矩形ABCD的边CD上有一动点E,连接AE,把△ADE沿着AE翻折,使点D落在边BC上的F点处(如图).
(1)求证:.
(2)若矩形ABCD的边AD=5,AB=4,求DE的长.
(3)若S△AEF=S△ABF+S△CEF,试判断的值与的值的大小关系,并证明你的判断.
6.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=2,AD=4,求EC的长;
(3)若AE﹣DE=2EC,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.
7.矩形ABCD中,AB=8,AD=12,将矩形折叠,使点A落在点P处,折痕为DE.
(1)如图1,若点P恰好在边BC上.
①求证:△EBP∽△PCD;
②求AE的长;
(2)如图2,若E是AB的中点,EP的延长线交BC于点F,求BF的长.
8.如图,正方形ABCD的对角线AC、BD交于点O,∠CBD的平分线BG交AC于E,交CD于F,且DG⊥BG.
(1)求证:BF=2DG;
(2)若BE,求BF的长.
9.如图,正方形ABCD的边长为1.对角线AC、BD相交于点O,P是BC延长线上的一点,AP交BD于点E,交CD于点H,OP交CD于点F,且EF与AC平行.
(1)求证:EF⊥BD.
(2)求证:四边形ACPD为平行四边形.
(3)求OF的长度.
10.根据相似多边形的定义,我们把四个角分别相等,四条边对应成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图1,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
(3)如图2,四边形ABCD中,AB∥CD,AC与BD相交于点O,过点O作EF∥AB分别交AD,BC于点E,F.记四边形ABFE的面积为S1,四边形EFCD的面积为S2,若四边形ABFE与四边形EFCD相似,求的值.
11.如图,平行四边形ABCD中,点P为CB延长线上点,连接DP交AC于点M、交AB于点N,已知DA=DC,∠ACD=45°.
(1)求证:四边形ABCD为正方形;
(2)连接BM,若N为AB的中点,求tan∠BMP的值;
(3)若MN=2,PN=6,求DM的长.
12.如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G.
(1)求四边形OEBF的面积;
(2)求证:OG BD=EF2;
(3)在旋转过程中,当△BEF与△COF的面积之和最大时,求AE的长.
13.如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,G在BC上移动,P是线段DF的中点,连接PG,PC.
(1)求∠DBF的大小;
(2)证明:DB∥PG;
(3)若∠BEF=60°,求PG:PC的值.
14.已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE;过点E作EG⊥AD交AC于点G.
(1)求证:四边形AFCE是菱形;
(2)求证:2AF2=AC AG;
(3)若AE=a,在△ABF中,AB>BF,△ABF的面积为b,且b,求tan∠OEG.
15.在 ABCD中,AC为对角线,点G在AB的延长线上,连接CG,点F在CG上,线段AF交BC于点E,若FA=FC,如图1.
(1)已知∠CAD=∠G,求证:AC2=CE BC;
(2)如图2,已知AF⊥BC,垂足为点E.
①若∠GCB=∠DAC,求证:AE=FE;
②若,AD=4,tan∠ABC=2,求BG的长.
16.在矩形ABCD中,点E在AB边上,CE=CD,过点B作BF∥CE交DE的延长线于点F,连接AF.
(1)如图1,求证:△AFB≌△CBE;
(2)如图2,连接BD交CE于点G,若CG=BF.
(i)求证:AF∥DG;
(ii)求的值.
17.如图,在菱形ABCD中,AB=6,∠B=60°,点E,F分别是AB,AD上的动点,满足AE=DF,连接CE,CF,EF,EF与AC交于点G.
(1)求∠ECF的度数;
(2)填空:
① ,
② ,
③ ;
(3)记△AEG的面积为S1,△AFG的面积为S2,△AEC的面积为S3,△AFC的面积为S4.
①若CF2=3AF FD,求的值;
②试判断的值是否存在最小值?若存在,求出这个值;若不存在,请说明理由.
18.在四边形ABCD中,点E为AB的中点,分别连接CE,DE.
(1)如图1,若∠A=∠B,∠ADE=∠BEC.
(i)求证:AE2=AD BC;
(ii)求证:DE平分∠ADC;
(2)如图2,若∠DAB+∠B=90°,∠DEC=90°,AD=3,BC=1,求CD的长.
19.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如1,在正方形ABCD中,E,F分别是AB、AD上两点,连接DE,CF,若AE=DF,求证:△AED≌△DFC;
(2)在(1)的条件下,求证:DE⊥CF;
(3)如图2,在矩形ABCD中,过点C作CE⊥BD交AD于点E,若,求的值;
(4)如图3,在四边形ABCD中,∠A=∠B=90°,E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于F,且AB=5,AD=3,CF=6,求DE的长.
参考答案
1.【解答】解:(1)如图1,过点P作PE⊥OA于点E.
∵PQ∥OA,PM∥OB,
∴四边形OMPQ为平行四边形,
∴PM=OQ=1,∠PME=∠AOB=60°,
∴PE=PM sin60°,ME,
∴CE=OC﹣OM﹣ME,
由勾股定理得;
(2)①证明:设OM=x,ON=y,
∵四边形OMPQ为菱形,
∴OQ=QP=OM=x,NQ=y﹣x,
∵PQ∥OA,
∴△NQP∽△NOC,
∴,
即,
∴6y﹣6x=xy,两边都除以6xy,得,
即;
②如图2,过点P作PE⊥OA于点E,过点N作NF⊥OA于点F,
则S1=OM PE,S2OC NF,
∴,
∵PM∥OB,
∴△CPM∽△CNO.
∴,
∴,
∵0<x<6,
∴.
2.【解答】(1)证明:∵BD是正方形ABCD的对角线,
∴∠ADB=∠CDB=45°,
∵四边形ABCD是正方形,
∴AD=CD,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴AG=CG;
(2)证明:∵四边形ABCD是正方形,
∴AD∥CB,
∴∠FCB=∠F,
由(1)可知△ADG≌△CDG,
∴∠DAG=∠DCG,
∴∠DAB﹣∠DAG=∠DCB﹣∠DCG,即∠BCF=∠BAG,
∴∠EAG=∠F,
又∠EGA=∠AGF,
∴△AEG∽△FAG;
(3)解:由(2)得△AEG∽△FAG,
∴,即GA2=GE GF=9,
∴GA=3或GA=﹣3(舍去),
故AG的长为3.
3.【解答】解:(1)∵四边形ABCD是矩形,
∴∠B=BAD=90°,AB=CD=8,AD=BC=6,
∴∠DAG+∠BAC=90°,
∵DG⊥AC,
∴∠DAG+∠ADE=90°,
∴∠BAC=∠ADE,
∴tan∠BAC=tan∠ADE,
∴,即:,
∴AE;
(2)如图1,过点F作FH⊥AC于点H,
∵CF平分∠ACD,FD⊥CD,FH⊥CA,
∴FD=FH,
∵∠ADC=90°,
∴AC10,
∵S△ACF+S△DCF=S△ACD,
∴AC FHCD FDAD CD,
∴10×FD8×FD6×8,
∴FD,
∴tan∠DCF;
(3)过点O1作O1N⊥AC于点N,过点O2作O2M⊥AC于点M,作O1K⊥O2M于点K,
则∠O1NMK是矩形,
∵DG AC=AD CD,
∴DG,
∴AG=DG tan∠ADE=DG,
∴CG=AC﹣AG=10,
∵O1、O2分别是Rt△ADG、Rt△DCG的内心,设⊙O1的半径为r1,⊙O2的半径为r2,
∴r1,r2,
∴O1K=MN=r1+r2,O2K=r2﹣r1,
∵∠O1KO2=90°,
∴O1O22.
4.【解答】解:(1)如图1中,
由折叠可知,∠AEB=∠FEB,∠DEG=∠HEG,
∵∠AEB+∠FEB+∠DEG+∠HEG=180°,
∴∠AEB+∠DEG=90°,
∵四边形ABCD是矩形,
∴∠A=∠D=∠AEB+∠ABE=90°,
∴∠ABE=∠DEG,
∴△ABE∽△DEG.
(2)①设AE=x,
∵△ABE∽△DEG,
∴,
∴,
∴DG(x﹣5)2,
∵0(0<x<10),
∴x=5时,DG有最大值,最大值为.
②如图2中,连接DH.
由折叠可知∠AEB=∠FEB,AE=EF,AB=BF=6,∠BFE=∠A=90°,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠FEB=∠EBC,
∴CE=CB=10,
∵点C在直线EF上,
∴∠BFC=90°,CF=10﹣EF=10﹣AE,
∴CF8,
∴AE=EF=CE﹣CF=10﹣8=2,
∴DG,
∴EG,
由折叠可知,EG垂直平分线段DH,
∴DH=22.
5.【解答】(1)证明:∵△ADE沿着AE翻折,使点D落在边BC上的F点处,
∴△AED≌△AFE,
∴∠CFE+∠BFA=90°,
∴∠AFE=∠D=90°,
在矩形ABCD中,∠B=∠C=90°,
∴∠BFA+∠BAF=90°,
∴∠CFE=∠BAF,
∴△ABF∽△FCE,
∴,
∵AB=CD,
∴;
(2)解:设ED=x,
∵CD=AB=4,
∴CE=4﹣x,FE=x,
又∵AF=AD=5,AB2+BF2=AF2,
∴BF3,
∴CF=5﹣3=2,
∵CF2+CE2=EF2,
∴22+(4﹣x)2=x2,
∴x,
∴DE;
(3)答:相等.
证明:∵S△AEF=S△ABF+S△EFC,
∴S△AEF,
过F作AB的平行线交AE于G,则(AB+CE)BC,
∴FG(AB+CE),
过E作EH⊥AB于H,交FG于M.
∵FG∥AB∥CE,
∴FM(BH+CE),
∴FM+GM(BH+AH+CE),
∴GMAH,
∴G,F分别为AE、BC中点.
在Rt△ABF中,BFBCAF.
∴∠BAF=30°,
∴∠BAF=∠CFE=∠EAF=30°,
∵∠ABF=∠AFE=∠FCE=90°,
∴△ABF∽△AEF,△AFE∽△FCE,
∴,,
∴AF2=AE AB,EF2=AE CE,
∴,
∴.
6.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
由翻折可知,∠D=∠AFE=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠CEF=90°,
∴∠AFB=∠FEC,
∴△ABF∽△FCE.
(2)设EC=x,
由翻折可知,AD=AF=4,
∴BF2,
∴CF=BC﹣BF=2,
∵△ABF∽△FCE,
∴,
∴,
∴x,
∴EC.
(3)∵△ABF∽△FCE,
∴,
∴tanα+tanβ,
设AB=CD=a,BC=AD=b,DE=x,
∴AE=DE+2CE=x+2(a﹣x)=2a﹣x,
∵AD=AF=b,DE=EF=x,∠B=∠C=∠D=90°,
∴BF,CF,
∵AD2+DE2=AE2,
∴b2+x2=(2a﹣x)2,
∴a2﹣axb2,
∵△ABF∽△FCE,
∴,
∴,
∴a2﹣ax ,
∴b2 ,
整理得,16a4﹣24a2b2+9b4=0,
∴(4a2﹣3b2)2=0,
∴,
∴tanα+tanβ.
7.【解答】解:(1)①∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,
∴∠BPE+∠BEP=90°,
由折叠知,∠DPE=∠BAD=90°,
∴∠BPE+∠CPD=90°,
∴∠BEP=∠CPD,
∵∠B=∠C=90°,
∴△EBP∽△PCD;
②∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=8,BC=AD=12,
由折叠知,PE=AE,DP=AD=12,
在Rt△DPC中,CP4,
∴BP=BC﹣CP=12﹣4,
在Rt△PBE中,PE2﹣BE2=BP2,
∴AE2﹣(8﹣AE)2=(12﹣4)2,
∴AE=18﹣6;
(2)如图,过点P作GH∥BC交AB于G,交CD于H.
则四边形AGHD是矩形,
设EG=x,则BG=4﹣x,
∵∠A=∠EPD=90°,∠EGP=∠DHP=90°,
∴∠EPG+∠DPH=90°,∠DPH+∠PDH=90°,
∴∠EPG=∠PDH,
∴△EGP∽△PHD,
∴,
∴PH=3EG=3x,DH=AG=4+x,
在Rt△PHD中,PH2+DH2=PD2,
∴(3x)2+(4+x)2=122,
解得x(负值已经舍弃),
∴BG=4,
在Rt△EGP中,GP,
∵GH∥BC,
∴△EGP∽△EBF,
∴,
∴,
∴BF=3.
8.【解答】(1)证明:延长DG、BC交于点H,
∵BG平分∠CBD,
∴∠1=∠2,
∵DG⊥BG,
∴∠BGD=∠BGH=90°,
又∵BG=BG,
∴△BGD≌△BGH(ASA),
∴BD=BH,
∴DH=2DG,
∵四边形ABCD是正方形,
∴BC=DC,∠BCF=∠DCH=90°,
又∵∠BGD=90°,∠3=∠4,
∴∠2=∠5,
∴△BCF≌△DCH(ASA),
∴BF=DH,
∴BF=2DG;
(2)∵四边形ABCD是正方形,
∴∠ACB=∠BDC=45°,
∴∠BCE=∠BDF,
又∵∠1=∠2,
∴△BEC∽△BFD,
∴,
∵BE,
∴BF.
9.【解答】(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∵EF∥AC,
∴EF⊥BD;
(2)证明:
∵EF∥AC,
∴,,
∵四边形ABCD是正方形,
∴AD∥CP,OA=OC,
∴,
即,
∴AO∥DP,
∵AD∥CP,
∴四边形ACPD为平行四边形;
(3)解:由勾股定理得:AC=BD,
∵四边形ACPD为平行四边形,
∴CP=AD=BC,
∴,
∵AD∥BP,
∴,
∴DEBD,OE=OD﹣DE,
∵DOBD,
∵∠DEF=∠DOC=90°﹣∠EDF=45°,
∴∠DFE=45°,
∴EF=DE,
在Rt△OEF中,由勾股定理得:OF.
10.【解答】(1)解:①四条边成比例的两个凸四边形相似,是假命题,角不一定相等.
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例.
③两个大小不同的正方形相似.是真命题.
故答案为假,假,真.
(2)证明:如图1中,连接BD,B1D1.
∵∠BCD=∠B1C1D1,且,
∴△BCD∽△B1C1D1,
∴∠CDB=∠C1D1B1,∠C1B1D1=∠CBD,
∵,
∴,
∵∠ABC=∠A1B1C1,
∴∠ABD=∠A1B1D1,
∴△ABD∽△A1B1D1,
∴,∠A=∠A1,∠ADB=∠A1D1B1,
∴,∠ADC=∠A1D1C1,∠A=∠A1,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,
∴四边形ABCD与四边形A1B1C1D1相似.
(3)如图2中,
∵四边形ABFE与四边形EFCD相似.
∴,
∵EF=OE+OF,
∴,
∵EF∥AB∥CD,
∴,,
∴,
∴,
∵AD=DE+AE,
∴,
∴2AE=DE+AE,
∴AE=DE,
∴四边形ABFE与四边形EFCD相似比为1
∴1.
11.【解答】(1)证明:∵四边形ABCD是平行四边形,DA=DC,
∴四边形ABCD是菱形,
∵DA=DC,
∴∠ACD=∠CAD=45°,
∴∠ADC=90°,
∴四边形ABCD为正方形;
(2)解:作BE⊥PD,如图所示:
则∠PEB=∠MEB=90°,
设正方形ABCD的边长为a,
∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AB=AD=a,∠PBN=∠DAB=∠BCD=90°,
∵N为AB的中点,
∴AN=BNABa,
在△BPN和△ADN中,,
∴△BPN≌△ADN(ASA),
∴BP=AD=a,PN=DNa,PC=BP+BC=2a,
∴PD=2DNa,
∵AD∥BC,
∴△ADM∽△CPM,
∴,
∴PMPDa,
∵∠PEB=∠PCD=90°,∠P=∠P,
∴△PBE∽△PDC,
∴,即,
解得:BEa,PEa,
∴EM=PM﹣PEa,
∴tan∠BMP;
(3)解:MN=2,PN=6,
∴MP=8,
∵AB∥CD,
∴AM:MC=MN:MD,
∵AD∥BC,
∴AM:MC=DM:MP,
∴MN:MD=DM:MP,
∴MD2=MN MP=2×8=16,
∴MD=4.
12.【解答】解:(1)∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOCS正方形ABCD1×1;
(2)证明:∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OG OB=OE2,
∵OBBD,OEEF,
∴OG BD=EF2;
(3)如图,过点O作OH⊥BC,
∵BC=1,
∴OHBC,
设AE=x,则BE=CF=1﹣x,BF=x,
∴S△BEF+S△COFBE BFCF OHx(1﹣x)(1﹣x)(x)2,
∵a0,
∴当x时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE.
13.【解答】解:(1)在菱形ABCD和菱形BEFG中,
∵∠DBC∠ABC,∠FBG∠EBG,
∵∠ABC+∠EBG=180°,
∴∠DBF=∠DBC+∠FBG=90°;
(2)如图,
延长GP交DC于点H,
∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP(ASA),
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH,
∴1,
∵∠HCG=∠DCB,
∴△CHG∽△CDB,
∴∠CGP=∠CBD,
∴DB∥PG;
(3)∵CG=CH,
∴△CHG是等腰三角形,
∴PG⊥PC,(三线合一)
又∵∠ABC=∠BEF=60°,
∴∠GCPBCD=60°,
∴.
14.【解答】(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AFCE是菱形.
(2)证明:∵EG⊥AD
∴∠AEG=90°,
∵∠AOE=90°,
∴∠AEG=∠AOE,
∵∠EAO=∠EAG,
∴△AOE∽△AEG,
∴,
∴AE2=AO AG,即2AF2=AC AG;
(3)解:∵四边形AFCE是菱形,
∴AF=AE=a,
在Rt△ABF中,AB2+BF2=AF2,
∴AB2+BF2=a2,
∴(AB+BF)2﹣2AB BF=a2①,
∵△ABF的面积为b,
∴AB BF=b,
∴AB BF=2b②,
由①、②得:(AB+BF)2=a2+4b,
∵AB+BF>0,
∴AB+BFa,
设DE=x,则CD=(a﹣x),则
x(a﹣x)=b,
解得x1a,x2a(舍去),
∴CDa,
∵∠EAG+∠EGA=∠OEG+∠EGA=90°,
∴∠EAG=∠OEG,
∴tan∠OEG=tan∠EAG.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠ABC=∠D,AD∥BC,
∴∠CAD=∠ACB,
∵∠CAD=∠G,
∴∠ACB=∠G,
∵∠ABC=∠G+∠BCG,∠ACG=∠ACB+∠BCG,
∴∠ABC=∠ACG,
∵FA=FC,
∴∠CAF=∠ACG,
∴∠ABC=∠CAF,
∵∠ACB=∠ECA,
∴△ACB∽△ECA,
∴,
∴AC2=CE BC;
(2)①证明:∵∠GCB=∠DAC,由(1)得∠CAD=∠ACB,
∴∠GCB=∠ACB,
∵AF⊥BC,
∴∠FEC=∠AEC=90°,
∵CE=CE,
∴△FEC≌△AEC(ASA),
∴AE=FE;
②解:过点F作 FH⊥AC于点H,延长AD与GC的延长线交于点K,如下图所示:
∵四边形ABCD为平行四边形,
∴,BC=AD=4,AB∥CD,BC∥AD,
又∵AE⊥BC,在Rt△ABE中,,
∴AE=2BE,
由勾股定理得AE2+BE2=AB2,
即,
∴BE=1,
∴AE=2BE=2,
∴CE=BC﹣BE=3,
在Rt△ACE中,由勾股定理得,
∵FA=FC,FH⊥AC,
∴,
∵,
∴,
在Rt△AFH中,由勾股定理得AF2﹣FH2=AH2,
即()2,
∴AF(负值舍去),
∴FE=AF﹣AE,
∵CE∥AK,
∴△CEF∽△KAF,
∴,
∴,
∴AK,
∵CD∥AG,
∴△KDC∽△KAG,
∴,
∴,
∴AG,
∴BG=AG﹣AB.
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠CDE=∠BEF,
∵BF∥CE,
∴∠CED=∠BFE,∠ABF=∠CEB,
∵CE=CD,
∴∠CDE=∠CED,AB=CE,
∴∠BEF=∠BFE,
∴BF=BE,
在△AFB和△CBE中,
,
∴△AFB≌△CBE(SAS);
(2)(i)证明:连接GF,如图2,
∵CG=BF,CG∥BF,
∴四边形BCGF为平行四边形,
∴GF=BC,GF∥BC,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴AD=GF,AD∥GF,
∴四边形ADGF为平行四边形,
∴AF∥DG;
(ii)解:∵BF=BE,CG=BF,
∴CG=BF=BE,
∵AB=CE,
∴EG=AE,
设CG=BF=BE=y,EG=AE=x,则AB=x+y,
∵AF∥DG,
∴∠BAF=∠EBG,
又∵∠ABF=∠BEG,
∴△ABF∽△BEG,
∴,
即,
解得,
又∵AF∥DB,
∴△AFE∽△BDE,
∴.
17.【解答】解:(1)在菱形ABCD中,∵AB=BC=CD=AD,且∠B=∠D=60°
∴△ABC,△ADC都是等边三角形,
∴AC=CD,∠CAE=60°=∠D=∠ACD.
∵AE=DF,
∴△AEC≌△DFC(SAS),
∴∠ACE=∠DCF,
∴∠ECF=60°;
(2)由(1)△ABC,△ADC都是等边三角形,
∴AB=AC=AD,
∵AE=DE,
∴①1,
②由(1)知△AEC≌△DFC,
∴CE=CF,
∵∠ECF=60°,
∴△CEF是等边三角形,
∴∠CFE=60°=∠CAF,
∵∠FCG=∠ACF,
∴△CFG∽△CAF,
∴,
∴,
∵AC=CD,CF=CE,
∴,
∴0;
③∵∠EAG=∠CFG=60°,∠AGE=∠CGF,
∴△AGE∽△FGC,
∴,
同理,,
∴1,
故答案为:1,0,1;
(3)①由△AGF∽△DFC可得,
即AF DF=AG CD=AG AC,
由△CGF∽△CFA可得,
即CF2=AC CG
∵CF=3AF FD,
∴CG=3AG,
∴AC=4AG,
∴;
②由(2)知△AEG∽△FCG,
∴∠AEG=∠FCG,
∵∠EAG=∠CAF=60°,
∴△AGE∽△AFC,
同理△AGF∽△AEC,
∴.
设AE=DF=x,
则,
当x=3时,的值最小,最小值为.
18.【解答】(1)证明:(i)∠A=∠B,∠ADE=∠BEC,
∴△AED∽△BCE,
∴,
∵E为AB的中点,
∴AE=BE,
∴,
即AE2=AD BC;
(ii)∵∠AED+∠DEC+∠CEB=180°,∠AED+∠ADE+∠A=180°,
∴∠A+∠ADE=∠DEC+∠CEB,
∵∠ADE=∠BEC,
∴∠A=∠DEC,
∵∠A=∠B,∠ADE=∠BEC,
∴△AED∽△BCE,
∴,
∵AE=BE,
∴,
∴△ADE∽△EDC,
∴∠ADE=∠EDC,
∴DE平分∠ADC;
(2)解:如图,过点A作AF∥BC,交CE的延长线于点F,连接DF,
∴∠FAE=∠B,
∵AE=BE,∠AEF=∠BEC,
∴△AEF≌△BEC(ASA),
∴AF=BC,EF=EC,
∵∠DAB+∠B=90°,
∴∠DAB+∠BAF=90°,
∴∠DAF=90°.
∵∠DEC=90°,
∴DF=DC,
在Rt△ADF中,AD2+AF2=DF2,
∵AD=3,BC=1,
∴AF=1,
∴CD=DF.
19.【解答】(1)证明:由正方形可知∠A=∠FDC=90°,AD=CD,
在△AED与△DFC中,
,
∴△AED≌△DFC(SAS);
(2)证明:由正方形性质可知∠ADE+∠AED=90°,
∵△AED≌△DFC(AAS),
∴∠DFC=∠AED,
∴∠DFC+∠ADE=90°,
∴DE⊥CF;
(3)解:如图2,设BD与CE交于点G,
由条件可知∠A=∠EDC=90°,AB=CD,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
∵,
∴;
(4)解:如图3,过点C作CH⊥AF交AF的延长线于点H,
由条件可知∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
