2025年数学中考专题一轮复习课件:4.21 图形的相似(共47张PPT)
文档属性
| 名称 | 2025年数学中考专题一轮复习课件:4.21 图形的相似(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 11:05:32 | ||
图片预览











文档简介
(共47张PPT)
2025年数学中考复习
4.21 图形的相似
基础知识
项目四 三角形
考点要求
壹
1.了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.
2.通过具体实例认识图形的相似,了解相似多边形和相似比.
3.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
4.了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似.了解相似三角形判定定理的证明.
5.了解相似三角形的性质定理;相似三角形对应线段的比等于相似比;相似三角形的面积比等于相似比的平方.
6.了解图形的位似,知道利用位似可以将一个图形放大或缩小.
7.会利用图形的相似解决一些简单的实际问题.
核心知识点
贰
概念
在四条线段中,如果其中两条线段的比 另外两条线段的比,即 ,那么这四条线段,b,,叫作成比例的线段,简称比例线段.
知识点1 比例线段及性质
等于
知识点2 比例的基本性质
基本性质 = ad=bc(a,b,c,d≠0)
合比性质 = =(b,d≠0)
等比性质 ==…=(b+d+…+n≠0)
=
知识点3 黄金分割
图示
概念
如图所示,点把线段分成和两条线段,且,那么就说线段 被点黄金分割,点叫作线段的黄金分割点, 与 的比叫作黄金比,即≈0.618,≈0.382.
【温馨提示】一条线段上有两个黄金分割点.
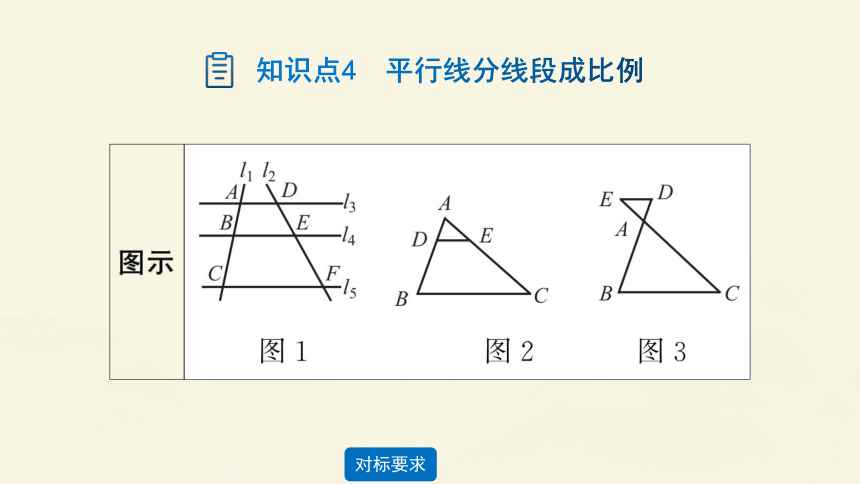
知识点4 平行线分线段成比例
基本事实 两条直线被一组平行线所截,所得的对应线段成比例.
如图1所示当l //l //l 时,有,等
推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.如图2、3所示,在△ADE和△ABC中,
∵DE//BC,
∴,,
知识点5 相似三角形的性质与判定
性质
(1)相似三角形的对应角相等,对应边成比例;
(2)相似三角形中的所有对应线段(高、中线、角平分线)成比例,且等于相似比;
(3)相似三角形的周长比等于相似比,面积比等于相似比的平方.
判定方法
(1)平行于三角形一边的直线和其他两边(或两边延长线)相交所构成的三角形与原三角形相似;
(2)两角对应相等的两个三角形相似;
(3)两边对应成比例且夹角相等的两个三角形相似;
(4)三边对应成比例的两个三角形相似.
【温馨提示】相似三角形的判定思路:
(1)有平行截线→用平行线的性质找等角;
(2)有一组等角,找
(3)有两组对应边成比例,找
知识点6 相似多边形
概念 各角对应相等,各边对应成比例的多边形叫作相似多边形,相似多边形对应边的比叫作相似比.
性质 (1)相似多边形的对应角相等,对应边(2)相似多边形的周长比等于相似比,成比例;面积比等于相似比的平方.
考点攻坚
叁
考点1 相似三角形的性质与判定
例1
(2022·北京 )已知△与△是位似图形,位似比是1∶3,则△与△的面积比( )
【解析】根据位似图形的面积比等于位似比的平方计算即可.∵与△是位似图形,位似比是1∶3,∴△与△的面积比为1∶9.故选C.
例2 (2020·贵阳)如图所示,在 中,,高,正方形一边在上,点分别在上,交 于点,则 的长为( )
A.15 B.20
C.25 D.30
【解析】
故选B.
考点2 相似三角形的应用
例3
(2022·成都)数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2m的标杆影长为1.2m,此时旗杆影长为7.2m,则旗杆的高度为 m.
【解析】根据同时、同地物高和影长的比不变,构造相似三角形,然后根据相似三角形的性质解答。设旗杆为AB,如图所示。
根据题意得△ABC△DEF,∴。∵DE=2 m,EF=1.2m,
BC=7.2 m,
∴=,解得AB=12 m
故答案为12。
考点3 黄金分割点
例4(2024·百色)宽与长的比是的矩形叫黄金矩形.心理测试表明:黄金矩形令人 赏心悦目,它给我们以协调、匀称的美感.现在,按照如下的步骤作图.第一步:作一个正方形;第二步:分别取的中点连接;第三步:以点为圆心,长为半径画弧,交的延长线于点;第四步:过点,交的延长线于.则所作图形中是黄金矩形的是( )
A.矩形 B.矩形
C. 矩形 D. 矩形
【解析】
专项训练
肆
提分训练
1.(2022·达州)如图所示,在△,则 ∶的值是(B )
A. B. C. D.
2.(2023·成都)如图所示,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m,同时量得小菲与镜子的水平距离为2m,镜子与旗杆的水平距离为10m,则旗杆高度为(B )
A.6.4m B.8m C.9.6m D.12.5m
电线杆顶端的影子刚好落在长方形广告牌的上边中点处,而长方形广告牌的影子刚好落在地面上点(如图),已知米,长方形广告牌的长米,高米,米,则电线杆的高度是 米.
3.(2024·南京)某学校旁有一根电线杆和一块长方形广告牌,有一天小明发现在太阳光照射下.
8.25
达标训练
4.(2022·杭州)如图所示,在中,,,的平分线,则点的黄金分割点.若,则 .
3
课堂练习
伍
1.(2024·云南)某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点,在近岸取点,使点共线且直线与河垂直,接着在过点且与垂直的直线上选择适当的点,确定与过点且垂直的直线的交点.如果测得m,m,m,则河的宽度是(C)
A.70m B.80m
C.90m D.100m
2.(2023·淄博)在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,,,在同一平面内,点,,在一条水平直线上.已知米,米,米,米,人从点远眺塔顶,视线恰好经过竹竿的顶端,可求出塔的高度.根据以上信息,塔的高度为 米.
18.2
3.如图所示,在中,点分别为边上的点,若添加条件: ,可使得相似.(任意写出一个满足条件的即可)
(答案不唯一)
4.(2023·崇左)如图所示,乐器上的一根弦80cm,两个端点固定在乐器面板上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,则支撑点之间的距离为 cm(结果保留根号)
(80)
5.(2024·九江)如图,在矩形中,若,,则的长为 .
6
6.(2022·常州)如图所示,在中,,将以点为中心逆时针旋转得到,点边上,于点.下列结论中所有正确结论的序号是(D)
①;②;③.
A.①②
B.②③
C.①③
D.①②③
7.(2024·荆州)如图,为边长等于4的等边三角形,点是边上的一个动点(不与点重合),,,垂足分别是.
(1)求证:;
(2)若,四边形面积为,求出之间的函数关系式,并写出的取值范围.
答案
8.(2023·丽水)探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
在中,,,边上一点,且(为正整数)边上的动点,过点的垂线交直线.
【初步感知】
(1)如图1,当时,兴趣小组探究得出结论:,请写出证明过程.
【深入探究】
(2)①如图2所示,当,且点在线段上时,试探究线段之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段之间数量关系的一般结论(直接写出结论,不必证明)
答案
答案
答案
答案
谢谢观看
2025年数学中考复习
4.21 图形的相似
基础知识
项目四 三角形
考点要求
壹
1.了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.
2.通过具体实例认识图形的相似,了解相似多边形和相似比.
3.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
4.了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似.了解相似三角形判定定理的证明.
5.了解相似三角形的性质定理;相似三角形对应线段的比等于相似比;相似三角形的面积比等于相似比的平方.
6.了解图形的位似,知道利用位似可以将一个图形放大或缩小.
7.会利用图形的相似解决一些简单的实际问题.
核心知识点
贰
概念
在四条线段中,如果其中两条线段的比 另外两条线段的比,即 ,那么这四条线段,b,,叫作成比例的线段,简称比例线段.
知识点1 比例线段及性质
等于
知识点2 比例的基本性质
基本性质 = ad=bc(a,b,c,d≠0)
合比性质 = =(b,d≠0)
等比性质 ==…=(b+d+…+n≠0)
=
知识点3 黄金分割
图示
概念
如图所示,点把线段分成和两条线段,且,那么就说线段 被点黄金分割,点叫作线段的黄金分割点, 与 的比叫作黄金比,即≈0.618,≈0.382.
【温馨提示】一条线段上有两个黄金分割点.
知识点4 平行线分线段成比例
基本事实 两条直线被一组平行线所截,所得的对应线段成比例.
如图1所示当l //l //l 时,有,等
推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.如图2、3所示,在△ADE和△ABC中,
∵DE//BC,
∴,,
知识点5 相似三角形的性质与判定
性质
(1)相似三角形的对应角相等,对应边成比例;
(2)相似三角形中的所有对应线段(高、中线、角平分线)成比例,且等于相似比;
(3)相似三角形的周长比等于相似比,面积比等于相似比的平方.
判定方法
(1)平行于三角形一边的直线和其他两边(或两边延长线)相交所构成的三角形与原三角形相似;
(2)两角对应相等的两个三角形相似;
(3)两边对应成比例且夹角相等的两个三角形相似;
(4)三边对应成比例的两个三角形相似.
【温馨提示】相似三角形的判定思路:
(1)有平行截线→用平行线的性质找等角;
(2)有一组等角,找
(3)有两组对应边成比例,找
知识点6 相似多边形
概念 各角对应相等,各边对应成比例的多边形叫作相似多边形,相似多边形对应边的比叫作相似比.
性质 (1)相似多边形的对应角相等,对应边(2)相似多边形的周长比等于相似比,成比例;面积比等于相似比的平方.
考点攻坚
叁
考点1 相似三角形的性质与判定
例1
(2022·北京 )已知△与△是位似图形,位似比是1∶3,则△与△的面积比( )
【解析】根据位似图形的面积比等于位似比的平方计算即可.∵与△是位似图形,位似比是1∶3,∴△与△的面积比为1∶9.故选C.
例2 (2020·贵阳)如图所示,在 中,,高,正方形一边在上,点分别在上,交 于点,则 的长为( )
A.15 B.20
C.25 D.30
【解析】
故选B.
考点2 相似三角形的应用
例3
(2022·成都)数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2m的标杆影长为1.2m,此时旗杆影长为7.2m,则旗杆的高度为 m.
【解析】根据同时、同地物高和影长的比不变,构造相似三角形,然后根据相似三角形的性质解答。设旗杆为AB,如图所示。
根据题意得△ABC△DEF,∴。∵DE=2 m,EF=1.2m,
BC=7.2 m,
∴=,解得AB=12 m
故答案为12。
考点3 黄金分割点
例4(2024·百色)宽与长的比是的矩形叫黄金矩形.心理测试表明:黄金矩形令人 赏心悦目,它给我们以协调、匀称的美感.现在,按照如下的步骤作图.第一步:作一个正方形;第二步:分别取的中点连接;第三步:以点为圆心,长为半径画弧,交的延长线于点;第四步:过点,交的延长线于.则所作图形中是黄金矩形的是( )
A.矩形 B.矩形
C. 矩形 D. 矩形
【解析】
专项训练
肆
提分训练
1.(2022·达州)如图所示,在△,则 ∶的值是(B )
A. B. C. D.
2.(2023·成都)如图所示,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m,同时量得小菲与镜子的水平距离为2m,镜子与旗杆的水平距离为10m,则旗杆高度为(B )
A.6.4m B.8m C.9.6m D.12.5m
电线杆顶端的影子刚好落在长方形广告牌的上边中点处,而长方形广告牌的影子刚好落在地面上点(如图),已知米,长方形广告牌的长米,高米,米,则电线杆的高度是 米.
3.(2024·南京)某学校旁有一根电线杆和一块长方形广告牌,有一天小明发现在太阳光照射下.
8.25
达标训练
4.(2022·杭州)如图所示,在中,,,的平分线,则点的黄金分割点.若,则 .
3
课堂练习
伍
1.(2024·云南)某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点,在近岸取点,使点共线且直线与河垂直,接着在过点且与垂直的直线上选择适当的点,确定与过点且垂直的直线的交点.如果测得m,m,m,则河的宽度是(C)
A.70m B.80m
C.90m D.100m
2.(2023·淄博)在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,,,在同一平面内,点,,在一条水平直线上.已知米,米,米,米,人从点远眺塔顶,视线恰好经过竹竿的顶端,可求出塔的高度.根据以上信息,塔的高度为 米.
18.2
3.如图所示,在中,点分别为边上的点,若添加条件: ,可使得相似.(任意写出一个满足条件的即可)
(答案不唯一)
4.(2023·崇左)如图所示,乐器上的一根弦80cm,两个端点固定在乐器面板上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,则支撑点之间的距离为 cm(结果保留根号)
(80)
5.(2024·九江)如图,在矩形中,若,,则的长为 .
6
6.(2022·常州)如图所示,在中,,将以点为中心逆时针旋转得到,点边上,于点.下列结论中所有正确结论的序号是(D)
①;②;③.
A.①②
B.②③
C.①③
D.①②③
7.(2024·荆州)如图,为边长等于4的等边三角形,点是边上的一个动点(不与点重合),,,垂足分别是.
(1)求证:;
(2)若,四边形面积为,求出之间的函数关系式,并写出的取值范围.
答案
8.(2023·丽水)探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
在中,,,边上一点,且(为正整数)边上的动点,过点的垂线交直线.
【初步感知】
(1)如图1,当时,兴趣小组探究得出结论:,请写出证明过程.
【深入探究】
(2)①如图2所示,当,且点在线段上时,试探究线段之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段之间数量关系的一般结论(直接写出结论,不必证明)
答案
答案
答案
答案
谢谢观看
同课章节目录
