第十四章一次函数 同步练习(含解析)
文档属性
| 名称 | 第十四章一次函数 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 948.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 16:51:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十四章一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数y=﹣中自变量x的取值范围是( )
A.x=3 B.x<3且x≠2 C.x≤3且x≠2 D.x≠2
2.如图所示,在一次“寻宝”游戏中,寻宝人已经找到两个标志点和,则藏宝处点的坐标是( )
A. B. C. D.
3.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系.已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
A.第24天的销售量为200件
B.第10天销售一件产品的利润是15元
C.第12天与第30天这两天的日销售利润相等
D.第30天的日销售利润是750元
4.平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5 B.6 C.7 D.8
5.下列不能准确表示地理位置的是( )
A.东经度,北纬度 B.方向南偏东,距离公里
C.距三明北动车站 D.排号
6.若(1,2)表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为( )
A.(2,1) B.(3,3) C.(2,3) D.(3,2)
7.下列语句能确定物体具体位置的是( )
A.楚王城大道东 B.政府广场右边
C.火车站附近1000米 D.东经113°,北纬31°
8.在同一个平面直角坐标系中,下列一次函数的对应图象与一次函数y=3x+2的图象没有交点的是( )
A.y=5x﹣3 B.y=﹣0.5x+1 C.y=3(x﹣2) D.y=4(x﹣5)
9.数对(1,3)表示第1组,第3行,那么小明坐第4组,第5行,用( )可以表示他的位置.
A.(4,5) B.(5,4) C.(4,4) D.(5,5)
10.已知点P(2a 1,1 a)在第一象限,则a的取值范围在数轴上表示正确的是
A. B. C. D.
11.地表以下的岩层温度y随着所处深度x的变化而变化,在某个地点y与x的关系可以由公式来表示,则y随x的增大而( ).
A.增大 B.减小 C.不变 D.以上答案都不对
12.一次函数的图象经过第四象限,与轴交于,且它的图象与坐标轴围成的三角形面积为3,则,的值为( )
A., B.,
C., D.,或,
二、填空题
13.在平面内两条互相 且 的数轴,就构成了平面直角坐标系.水平的数轴称为 轴或 轴,取向 的方向为正方向;竖直的数轴称为 轴, 又称 轴, 取向 的方向为正方向;两坐标轴的交点为平面直角坐标系的
14.已知一次函数的图像经过第一、二、四象限,且过点,则 (用含的代数式表示);的取值范围是 .
15.若为一次函数,则 .
16.一次函数 y1=kx+b 与 y2=x+a 的图象如图所示,则下列结论:①k<0;②a<0,b<0;③当 x=3 时,y1=y2;④不等式 kx+b>x+a 的解集是 x<3,其中正确的结论有 .(只填序号)
17.如图,在长方形中,一只蚂蚁从点出发,沿着循环爬行,其中点的坐标为,C点的坐标为,D点的坐标为,当蚂蚁爬行了个单位长度时,它所处位置的坐标为 .
三、解答题
18.某汽车运输公司根据实际需要计划购买大、中型两种客车共辆,已知大型客车每辆万元,中型客车每辆万元,设购买中型客车辆,购买总费用为万元.
求与的函数关系式;
若要求购买中型客车不超过辆,那么该公司怎样购买最省钱?
19.一一只甲虫在的方格(每小格边长为上沿着网格线运动.它从处出发去看望、、处的其它甲虫、、、都在格点上).规定:向上向右走为正,向下向左走为负.若从到记为:,则从到记为:,其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)图中_____,_____,_____,______,______, ;
(2)若这只甲虫的行走路线为,请计算该甲虫走过的路程;
(3)若这只甲虫从处去甲虫处的行走路线依次为,,,,请在图中标出的位置;若甲虫每走需消耗1.5焦耳的能量,则甲虫从走到的过程中共需要消耗多少焦耳的能量?
(4)若图中另有两个格点、,且,,则应记为多少?
20.已知一次函数y=(m+3)x+m﹣4,y随x的增大而增大.
(1)求m的取值范围;
(2)如果这个一次函数又是正比例函数,求m的值.
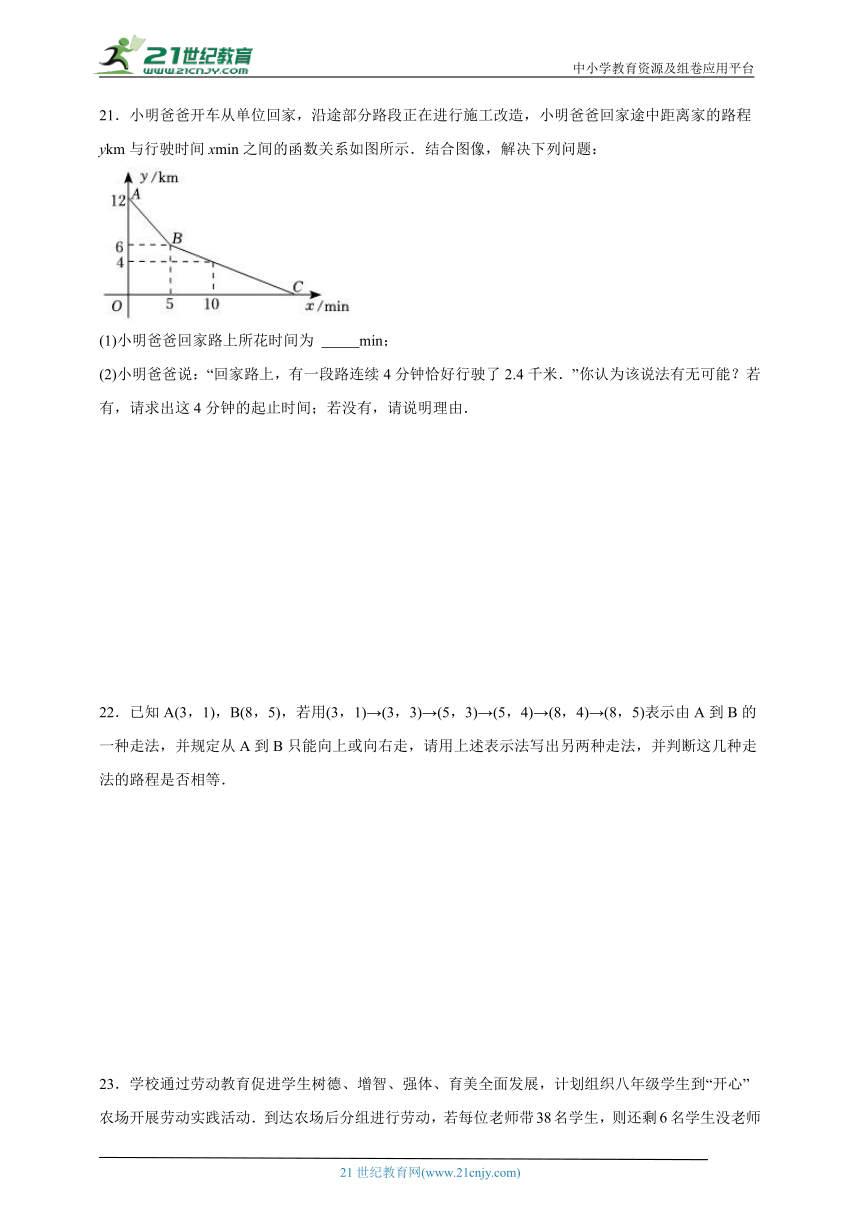
21.小明爸爸开车从单位回家,沿途部分路段正在进行施工改造,小明爸爸回家途中距离家的路程ykm与行驶时间xmin之间的函数关系如图所示.结合图像,解决下列问题:
(1)小明爸爸回家路上所花时间为 min;
(2)小明爸爸说:“回家路上,有一段路连续4分钟恰好行驶了2.4千米.”你认为该说法有无可能?若有,请求出这4分钟的起止时间;若没有,请说明理由.
22.已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.
23.学校通过劳动教育促进学生树德、增智、强体、育美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动.到达农场后分组进行劳动,若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生.劳动实践结束后,学校在租车总费用元的限额内,租用汽车送师生返校,每辆车上至少要有名老师.现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 乙型客车
载客量/(人/辆)
租金/(元/辆)
(1)租车返校时,既要保证所有师生都有车坐,又要保证每辆车上至少有名老师,则共需租车__________辆;
(2)若设租用甲客车辆,租车费用为元,请写出与的函数关系式(不要求写自变量取值范围);
(3)学校共有几种租车方案?最少租车费用是多少?
24.如图,在平面直角坐标系中,一次函数的图象与正比例函数的图象交于点.
(1)求m,n的值;
(2)设一次函数的图象与x轴交于点B,与y轴交于点C,求点B,点C的坐标;
(3)写出使函数的值小于函数的值的自变量x的取值范围;
(4)在x轴上是否存在点P使为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
《第十四章一次函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A C C D C A C
题号 11 12
答案 A A
1.C
【分析】根据被开方数是非负数,分母不能为零列不等式组求解.
【详解】解:由题意得: 3﹣x≥0且x﹣2≠0,
解得:x≤3且x≠2.
故选:C.
【点睛】本题主要考查了函数自变量的取值范围,根据被开方数是非负数、分母不能为零列出不等式组是解答本题的关键.
2.B
【分析】本题考查了平面直角坐标系中点的坐标的确定,根据已知点的坐标确定平面直角坐标系,由此即可求.
已知点和,画出直角坐标系,即可求解.
【详解】解:已知点和,
建立平面直角坐标系如图所示,
∴
故选: B.
3.C
【分析】本题考查的是一次函数的应用,利用待定系数法求解一次函数的解析式,从函数图象中获取信息.由图①的信息可判断A;再求解一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系式,计算当时,,可判断B;再求解当时,设产品日销售量y(单位:件)与时间t(单位:天)的函数关系式:分别计算第12天与第30天的销售量与当天一件产品的销售利润,从而可判断C和D.
【详解】解:由图①中的信息可得:第24天的销售量为200件,故A不符合题意;
设当时,一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系为:
,
,
解得:,
,
当时,,
所以第10天销售一件产品的利润是15元,故B不符合题意;
当时,设产品日销售量y(单位:件)与时间t(单位:天)的函数关系为:
,
,
解得:,
,
当时,,,
所以第12天的日销售利润为:元,
第30天的日销售利润为:元,而,故C符合题意;
由第30天的日销售利润为:元,故D不符合题意,
故选:C.
4.A
【详解】解:构造等腰三角形,
①分别以A,B为圆心,以AB的长为半径作圆;
②作AB的中垂线.
如图,一共有5个C点,
注意,与B重合及与AB共线的点要排除.
故选A.
5.C
【分析】根据确定具体位置需要两个元素,结合实际进行判断即可.
【详解】解:A.东经度,北纬度,能准确表示地理位置,不合题意;
B.方向南偏东,距离公里,能准确表示地理位置,不合题意;
C.距三明北动车站,不能准确表示地理位置,符合题意;
D.排号,能准确表示地理位置,不合题意;
故选:C.
【点睛】本题主要考查生活中确定具体位置的实际应用,解题的关键是理解确定具体位置的方法.
6.C
【分析】根据数对(1,2)表示教室里第1列第2排的位置,可知第一个数字表示列,第二个数字表示排,由此即可求得答案.
【详解】∵(1,2)表示教室里第1列第2排的位置,
∴教室里第2列第3排的位置表示为(2,3),
故选C.
【点睛】本题考查了数对表示位置的方法的灵活应用,分析出数对表示的意义是解题的关键.
7.D
【分析】根据坐标可以表示位置即可得出结论.
【详解】解:对于ABC选项的描述都不能确定物体的具体位置,D选项的描述能确定物体具体位置.
故选:D.
【点睛】本题主要考查了利用坐标确定位置,熟练掌握其概念是解决本题的关键.
8.C
【分析】逐项判断各选项的比例系数是否等于3,即可判断与一次函数y=3x+2的图象是否有交点.
【详解】解:A. y=5x﹣3,比例系数为5≠3,所以直线y=5x﹣3与直线y=3x+2相交,有交点,不合题意;
B. y=﹣0.5x+1,比例系数为-0.5≠3,所以直线y=﹣0.5x+1与直线y=3x+2相交,有交点,不合题意;
C. y=3(x﹣2)=3x-6,比例系数为3,所以直线y=3(x﹣2)与直线y=3x+2平行,没有交点,符合题意;
D. y=4(x﹣5)=4x-20,比例系数为4≠3,所以直线y=4(x﹣5)与直线y=3x+2相交,有交点,不合题意.
故选:C
【点睛】本题考查了平面直角坐标系中两条直线平行的条件,当两条直线的函数解析式中比例系数相等时,两条直线平行,否则相交.
9.A
【分析】根据题意可知数对中的第一个数表示“组数”,第二个数表示“行数”,据此即可作答.
【详解】∵数对(1,3)表示第1组,第3行,
∴小明坐第4组,第5行,用数对表示为(4,5),
故选:A.
【点睛】此题主要考查了用数对表示位置的方法,理解题意是解答本题的基础.
10.C
【分析】根据点的坐标,可得一元一次不等式组,根据解一元一次不等式,可得不等式组的解集,可得答案.
【详解】∵点P(2a 1,1 a)在第一象限,
∴,
解得,
∴,
故选C
【点睛】本题考查了点的坐标及在数轴上表示不等式组的解集:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
11.A
【分析】根据一次函数的性质,即可求解.
【详解】解:∵ 35>0,
∴y随x的增大而增大.
故选:A
【点睛】此题主要考查了一次函数的图象性质,只有掌握它的性质才能灵活解题.
12.A
【分析】先把点坐标代入可计算出的值,再用表示一次函数与轴的交点坐标,然后根据三角形面积公式得到,再解方程即可得到的值.
【详解】解:把代入得,
把代入得,解得,则一次函数图象与轴的交点坐标为,,
一次函数的图象经过第四象限,与轴交于,
,
一次函数的图象与两坐标轴围成的三角形面积为3,
,解得,
即,.
故选:A.
【点睛】本题考查了一次函数图形上点的坐标特征:一次函数,,且,为常数)的图象是一条直线.它与轴的交点坐标是,;与轴的交点坐标是;直线上任意一点的坐标都满足函数关系式.
13.见解析
【详解】试题解析:平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.水平的数轴称为轴或横轴,习惯上取向右为正方向;竖直的数轴为轴或纵轴,取向上方向为正方向;两个坐标轴的交点为平面直角坐标系的坐标原点.
故答案为垂直、原点重合,,横,右,,纵,上,原点.
14.
【分析】若一次函数的图像经过第一、二、四象限,可知,再根据函数过点,将该点代入一次函数解析式,得出k与b的关系式,最后再利用,求出k的取值范围.
【详解】解:∵,过点
∴
∴
又∵一次函数图像过第一、二、四象限 ,
∴
即
解得:
【点睛】本题考查一元一次函数的性质,考查不等式组的解法.
15.3或5
【分析】本题考查一次函数的定义.根据一次函数的定义可得自变量的次数为1,且系数不为零可得关于m的方程,然后求解即可.
【详解】解:∵是一次函数,
∴,且,
解得:或3.
故答案为:3或5.
16.①③④
【分析】仔细观察图象,①k的正负看函数图象从左向右成何趋势即可;②a,b看y2=x+a, y1=kx+b与y轴的交点坐标;③看两函数图象的交点横坐标;④以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大.
【详解】解:① y1=kx+b的图象从左向右呈下降趋势,k<0正确;
② y2=x+a与y轴的交点在负半轴上, a<0,另一条直线与y轴交于正半轴,所以b>0,故②错误;
③两函数图象的交点横坐标为3,
当x=3时, y1=y2 ,故③正确;
④当x<3时, y1>y2 ,故④正确;
故正确的判断是①③④.
故答案为: ①③④.
【点睛】此题主要考查了一次函数的图象,考查学生的分析能力和读图能力,一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0,函数y=kx+b的图象经过第二、三、四象限.
17.
【分析】根据点的坐标,得到,,进而得出蚂蚁爬行一圈的长度为个单位,再根据,得出所处位置为边中点,即可得到坐标.
【详解】解:点的坐标为,C点的坐标为,D点的坐标为,
,,
长方形,
,,
蚂蚁从点出发,爬行一圈的长度为,
,
又,,
蚂蚁爬行了个单位长度时,它所处位置为边中点,
坐标为,
故答案为:.
【点睛】本题考查了坐标与图形,两点的距离公式,利用数形结合的思想解决问题是解题关键.
18.(1);(2)该公司购买辆中型客车,辆大型客车时最省钱.
【分析】(1)根据购车的数量以及价格根据总费用直接表示出等式;
(2)根据购买中型客车的数量不超过12辆,得出,中x的取值范围,再根据y随着x的增大而减小,得出x的值.
【详解】解:(1)与的函数关系式为:;
(2)∵,
∴,
∴的值随的增大而减小.
∵,
∴当时,的值最小,
∴该公司购买辆中型客车,辆大型客车时最省钱.
【点睛】此题主要考查了一次函数的应用以及增减性,得出x取值范围再利用增减性得出x的值是解决问题的关键.
19.见解析
【分析】
(1)根据题中的计数方法即可得到结果;
(2)根据题意列出算式,计算即可得到结果;
(3)在图形中找出的位置,根据题意列出算式,计算即可得到结果;
(4)由,,得到到的过程,即可确定出.
【详解】
解:(1)根据题意得:图中,,;
(2)根据题意得:;
(3)如图所示,为甲虫子走过的路程为,
则甲虫从走到的过程中共需要消耗的能量为(焦耳);
(4)由,,
得到向右2个单位,向上3个单位到达,即应记为,
故答案为:(1);;;0;;;(4)
【点睛】此题考查了有理数的加减混合运算,正数与负数,解题的关键是正确的理解从一个点到另一个点移动时,如何用坐标表示.
20.(1)m>﹣3;(2)m=4.
【详解】试题分析:(1)直接利用一次函数的增减性得出m的取值范围;
(2)直接利用正比例函数的定义得出m的值.
解:(1)∵一次函数y=(m+3)x+m﹣4,y随x的增大而增大,
∴m+3>0,
解得:m>﹣3;
(2)∵y=(m+3)x+m﹣4是正比例函数,
∴m﹣4=0,
解得:m=4.
21.(1)20
(2)从第4分钟到第8分钟
【分析】(1)用待定系数法求出直线BC的解析式,然后求出C点坐标即可;
(2)分别计算AB段和BC的速度作比较即可得出结论.
【详解】(1)解:设直线BC的解析式为y=kx+b,
代入点(5,6)和(10,4)
得,
解得:,
∴直线BC的解析式为,
当y=0时,x=20,
故答案为:20;
(2)由题知:
AB段的速度为:(12-6)÷5=1.2(km/min),
BC段的速度为:(6-4)÷(10-5)=0.4(km/min),
4分钟行驶了2.4千米的平均速度为:2.4÷4=0.6(km/min),
则小明爸爸连续的四分钟有一段在AB段有一段在BC段,
设在AB段行驶时间为x min,则在BC段行驶(4-x)min,
由题意得1.2x+(4-x)×0.4=2.4,
解得x=1,
5-1=4(min),4+4=8(min),
∴这4分钟的起止时间是从第4分钟到第8分钟.
【点睛】本题主要考查一次函数的应用,熟练掌握待定系数法求一次函数是解题的关键.
22.走法一:(3,1)→(6,1)→(6,2)→(7,2)→(8,2)→(8,5);走法二:(3,1)→(3,2)→(3,5)→(4,5)→(7,5)→(8,5).(答案不唯一).这几种走法的路程相等.
【分析】根据题意,走法有多种,只要符合只能向上或向右走即可,通过走的路径可判断这些走法的路程相等.
【详解】
走法一:(3,1)→(6,1)→(6,2)→(7,2)→(8,2)→(8,5);
走法二:(3,1)→(3,2)→(3,5)→(4,5)→(7,5)→(8,5).(答案不唯一).
这几种走法的路程相等.
【点睛】本题考查了坐标确定位置:平面直角坐标系中点与有序实数对一一对应.
23.(1)
(2)
(3)学校共有两种租车方案,最少费用为元
【分析】本题主要考查了一元一次方程的实际应用,一元一次不等式组的实际应用,一次函数的实际应用,解题的关键是正确理解题意,根据题意找出数量关系,列出方程、不等式组、一次函数表达式.
(1)设参加本次实践活动的老师有名,根据“若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生”列出方程求解即可;
(2)根据题意列函数关系式即可;
(3)根据题意列不等式,求解不等式,然后根据随的增大而增大,求解即可;
【详解】(1)解:设老师有名,学生有名,
根据题意,得解得,
老师有名,学生有名;
每辆车上至少有名老师,
汽车总数不能大于辆,
,
要保证名师生有车坐,汽车总数不能少于(取整数)辆,
共需租车辆.
(2);
(3)学校在租车总费用元的限额内,租用汽车送师生返校,
,
,即.
,
要保证名师生有车坐,
,
,
,
有两种租车方案:
方案一:租辆甲型客车,辆乙型客车;
方案二:租辆甲型客车,辆乙型客车;
,
随的增大而增大,
当时,y最小,.
答:学校共有两种租车方案,最少费用为元.
24.(1),
(2)点B坐标为,点C坐标为
(3)
(4)存在,点P坐标为或或或
【分析】(1)待定系数法求出m,n的值即可;
(2)令,分别求出相应的函数值和自变量,即可得出结果;
(3)结合图象法,即可得出结论;
(4)分三边两两相等,三种情况,进行讨论求解即可.
【详解】(1)正比例函数的图象过点.
,
.
又一次函数的图象过点
,
.
(2)解:由(1)可得,一次函数的解析式为,
令,则
,
点B坐标为,
令,则,
点C坐标为;
(3)解:由图象可知:在A点右侧,函数的值小于函数的值;
故;
(4)存在,点P坐标为或或或.
点,
,
当时,且点P在x轴上,
则点或;
当时,如图,过点A作于E,
则点,
,,
,
点;
当时,
,
,
点,
综上所述:点P坐标为或或或.
【点睛】本题考查一次函数的综合应用.正确的求出函数解析式,利用数形结合和分类讨论的思想,进行求解,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十四章一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数y=﹣中自变量x的取值范围是( )
A.x=3 B.x<3且x≠2 C.x≤3且x≠2 D.x≠2
2.如图所示,在一次“寻宝”游戏中,寻宝人已经找到两个标志点和,则藏宝处点的坐标是( )
A. B. C. D.
3.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系.已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
A.第24天的销售量为200件
B.第10天销售一件产品的利润是15元
C.第12天与第30天这两天的日销售利润相等
D.第30天的日销售利润是750元
4.平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5 B.6 C.7 D.8
5.下列不能准确表示地理位置的是( )
A.东经度,北纬度 B.方向南偏东,距离公里
C.距三明北动车站 D.排号
6.若(1,2)表示教室里第1列第2排的位置,则教室里第2列第3排的位置表示为( )
A.(2,1) B.(3,3) C.(2,3) D.(3,2)
7.下列语句能确定物体具体位置的是( )
A.楚王城大道东 B.政府广场右边
C.火车站附近1000米 D.东经113°,北纬31°
8.在同一个平面直角坐标系中,下列一次函数的对应图象与一次函数y=3x+2的图象没有交点的是( )
A.y=5x﹣3 B.y=﹣0.5x+1 C.y=3(x﹣2) D.y=4(x﹣5)
9.数对(1,3)表示第1组,第3行,那么小明坐第4组,第5行,用( )可以表示他的位置.
A.(4,5) B.(5,4) C.(4,4) D.(5,5)
10.已知点P(2a 1,1 a)在第一象限,则a的取值范围在数轴上表示正确的是
A. B. C. D.
11.地表以下的岩层温度y随着所处深度x的变化而变化,在某个地点y与x的关系可以由公式来表示,则y随x的增大而( ).
A.增大 B.减小 C.不变 D.以上答案都不对
12.一次函数的图象经过第四象限,与轴交于,且它的图象与坐标轴围成的三角形面积为3,则,的值为( )
A., B.,
C., D.,或,
二、填空题
13.在平面内两条互相 且 的数轴,就构成了平面直角坐标系.水平的数轴称为 轴或 轴,取向 的方向为正方向;竖直的数轴称为 轴, 又称 轴, 取向 的方向为正方向;两坐标轴的交点为平面直角坐标系的
14.已知一次函数的图像经过第一、二、四象限,且过点,则 (用含的代数式表示);的取值范围是 .
15.若为一次函数,则 .
16.一次函数 y1=kx+b 与 y2=x+a 的图象如图所示,则下列结论:①k<0;②a<0,b<0;③当 x=3 时,y1=y2;④不等式 kx+b>x+a 的解集是 x<3,其中正确的结论有 .(只填序号)
17.如图,在长方形中,一只蚂蚁从点出发,沿着循环爬行,其中点的坐标为,C点的坐标为,D点的坐标为,当蚂蚁爬行了个单位长度时,它所处位置的坐标为 .
三、解答题
18.某汽车运输公司根据实际需要计划购买大、中型两种客车共辆,已知大型客车每辆万元,中型客车每辆万元,设购买中型客车辆,购买总费用为万元.
求与的函数关系式;
若要求购买中型客车不超过辆,那么该公司怎样购买最省钱?
19.一一只甲虫在的方格(每小格边长为上沿着网格线运动.它从处出发去看望、、处的其它甲虫、、、都在格点上).规定:向上向右走为正,向下向左走为负.若从到记为:,则从到记为:,其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)图中_____,_____,_____,______,______, ;
(2)若这只甲虫的行走路线为,请计算该甲虫走过的路程;
(3)若这只甲虫从处去甲虫处的行走路线依次为,,,,请在图中标出的位置;若甲虫每走需消耗1.5焦耳的能量,则甲虫从走到的过程中共需要消耗多少焦耳的能量?
(4)若图中另有两个格点、,且,,则应记为多少?
20.已知一次函数y=(m+3)x+m﹣4,y随x的增大而增大.
(1)求m的取值范围;
(2)如果这个一次函数又是正比例函数,求m的值.
21.小明爸爸开车从单位回家,沿途部分路段正在进行施工改造,小明爸爸回家途中距离家的路程ykm与行驶时间xmin之间的函数关系如图所示.结合图像,解决下列问题:
(1)小明爸爸回家路上所花时间为 min;
(2)小明爸爸说:“回家路上,有一段路连续4分钟恰好行驶了2.4千米.”你认为该说法有无可能?若有,请求出这4分钟的起止时间;若没有,请说明理由.
22.已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.
23.学校通过劳动教育促进学生树德、增智、强体、育美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动.到达农场后分组进行劳动,若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生.劳动实践结束后,学校在租车总费用元的限额内,租用汽车送师生返校,每辆车上至少要有名老师.现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 乙型客车
载客量/(人/辆)
租金/(元/辆)
(1)租车返校时,既要保证所有师生都有车坐,又要保证每辆车上至少有名老师,则共需租车__________辆;
(2)若设租用甲客车辆,租车费用为元,请写出与的函数关系式(不要求写自变量取值范围);
(3)学校共有几种租车方案?最少租车费用是多少?
24.如图,在平面直角坐标系中,一次函数的图象与正比例函数的图象交于点.
(1)求m,n的值;
(2)设一次函数的图象与x轴交于点B,与y轴交于点C,求点B,点C的坐标;
(3)写出使函数的值小于函数的值的自变量x的取值范围;
(4)在x轴上是否存在点P使为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
《第十四章一次函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C A C C D C A C
题号 11 12
答案 A A
1.C
【分析】根据被开方数是非负数,分母不能为零列不等式组求解.
【详解】解:由题意得: 3﹣x≥0且x﹣2≠0,
解得:x≤3且x≠2.
故选:C.
【点睛】本题主要考查了函数自变量的取值范围,根据被开方数是非负数、分母不能为零列出不等式组是解答本题的关键.
2.B
【分析】本题考查了平面直角坐标系中点的坐标的确定,根据已知点的坐标确定平面直角坐标系,由此即可求.
已知点和,画出直角坐标系,即可求解.
【详解】解:已知点和,
建立平面直角坐标系如图所示,
∴
故选: B.
3.C
【分析】本题考查的是一次函数的应用,利用待定系数法求解一次函数的解析式,从函数图象中获取信息.由图①的信息可判断A;再求解一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系式,计算当时,,可判断B;再求解当时,设产品日销售量y(单位:件)与时间t(单位:天)的函数关系式:分别计算第12天与第30天的销售量与当天一件产品的销售利润,从而可判断C和D.
【详解】解:由图①中的信息可得:第24天的销售量为200件,故A不符合题意;
设当时,一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系为:
,
,
解得:,
,
当时,,
所以第10天销售一件产品的利润是15元,故B不符合题意;
当时,设产品日销售量y(单位:件)与时间t(单位:天)的函数关系为:
,
,
解得:,
,
当时,,,
所以第12天的日销售利润为:元,
第30天的日销售利润为:元,而,故C符合题意;
由第30天的日销售利润为:元,故D不符合题意,
故选:C.
4.A
【详解】解:构造等腰三角形,
①分别以A,B为圆心,以AB的长为半径作圆;
②作AB的中垂线.
如图,一共有5个C点,
注意,与B重合及与AB共线的点要排除.
故选A.
5.C
【分析】根据确定具体位置需要两个元素,结合实际进行判断即可.
【详解】解:A.东经度,北纬度,能准确表示地理位置,不合题意;
B.方向南偏东,距离公里,能准确表示地理位置,不合题意;
C.距三明北动车站,不能准确表示地理位置,符合题意;
D.排号,能准确表示地理位置,不合题意;
故选:C.
【点睛】本题主要考查生活中确定具体位置的实际应用,解题的关键是理解确定具体位置的方法.
6.C
【分析】根据数对(1,2)表示教室里第1列第2排的位置,可知第一个数字表示列,第二个数字表示排,由此即可求得答案.
【详解】∵(1,2)表示教室里第1列第2排的位置,
∴教室里第2列第3排的位置表示为(2,3),
故选C.
【点睛】本题考查了数对表示位置的方法的灵活应用,分析出数对表示的意义是解题的关键.
7.D
【分析】根据坐标可以表示位置即可得出结论.
【详解】解:对于ABC选项的描述都不能确定物体的具体位置,D选项的描述能确定物体具体位置.
故选:D.
【点睛】本题主要考查了利用坐标确定位置,熟练掌握其概念是解决本题的关键.
8.C
【分析】逐项判断各选项的比例系数是否等于3,即可判断与一次函数y=3x+2的图象是否有交点.
【详解】解:A. y=5x﹣3,比例系数为5≠3,所以直线y=5x﹣3与直线y=3x+2相交,有交点,不合题意;
B. y=﹣0.5x+1,比例系数为-0.5≠3,所以直线y=﹣0.5x+1与直线y=3x+2相交,有交点,不合题意;
C. y=3(x﹣2)=3x-6,比例系数为3,所以直线y=3(x﹣2)与直线y=3x+2平行,没有交点,符合题意;
D. y=4(x﹣5)=4x-20,比例系数为4≠3,所以直线y=4(x﹣5)与直线y=3x+2相交,有交点,不合题意.
故选:C
【点睛】本题考查了平面直角坐标系中两条直线平行的条件,当两条直线的函数解析式中比例系数相等时,两条直线平行,否则相交.
9.A
【分析】根据题意可知数对中的第一个数表示“组数”,第二个数表示“行数”,据此即可作答.
【详解】∵数对(1,3)表示第1组,第3行,
∴小明坐第4组,第5行,用数对表示为(4,5),
故选:A.
【点睛】此题主要考查了用数对表示位置的方法,理解题意是解答本题的基础.
10.C
【分析】根据点的坐标,可得一元一次不等式组,根据解一元一次不等式,可得不等式组的解集,可得答案.
【详解】∵点P(2a 1,1 a)在第一象限,
∴,
解得,
∴,
故选C
【点睛】本题考查了点的坐标及在数轴上表示不等式组的解集:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
11.A
【分析】根据一次函数的性质,即可求解.
【详解】解:∵ 35>0,
∴y随x的增大而增大.
故选:A
【点睛】此题主要考查了一次函数的图象性质,只有掌握它的性质才能灵活解题.
12.A
【分析】先把点坐标代入可计算出的值,再用表示一次函数与轴的交点坐标,然后根据三角形面积公式得到,再解方程即可得到的值.
【详解】解:把代入得,
把代入得,解得,则一次函数图象与轴的交点坐标为,,
一次函数的图象经过第四象限,与轴交于,
,
一次函数的图象与两坐标轴围成的三角形面积为3,
,解得,
即,.
故选:A.
【点睛】本题考查了一次函数图形上点的坐标特征:一次函数,,且,为常数)的图象是一条直线.它与轴的交点坐标是,;与轴的交点坐标是;直线上任意一点的坐标都满足函数关系式.
13.见解析
【详解】试题解析:平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.水平的数轴称为轴或横轴,习惯上取向右为正方向;竖直的数轴为轴或纵轴,取向上方向为正方向;两个坐标轴的交点为平面直角坐标系的坐标原点.
故答案为垂直、原点重合,,横,右,,纵,上,原点.
14.
【分析】若一次函数的图像经过第一、二、四象限,可知,再根据函数过点,将该点代入一次函数解析式,得出k与b的关系式,最后再利用,求出k的取值范围.
【详解】解:∵,过点
∴
∴
又∵一次函数图像过第一、二、四象限 ,
∴
即
解得:
【点睛】本题考查一元一次函数的性质,考查不等式组的解法.
15.3或5
【分析】本题考查一次函数的定义.根据一次函数的定义可得自变量的次数为1,且系数不为零可得关于m的方程,然后求解即可.
【详解】解:∵是一次函数,
∴,且,
解得:或3.
故答案为:3或5.
16.①③④
【分析】仔细观察图象,①k的正负看函数图象从左向右成何趋势即可;②a,b看y2=x+a, y1=kx+b与y轴的交点坐标;③看两函数图象的交点横坐标;④以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大.
【详解】解:① y1=kx+b的图象从左向右呈下降趋势,k<0正确;
② y2=x+a与y轴的交点在负半轴上, a<0,另一条直线与y轴交于正半轴,所以b>0,故②错误;
③两函数图象的交点横坐标为3,
当x=3时, y1=y2 ,故③正确;
④当x<3时, y1>y2 ,故④正确;
故正确的判断是①③④.
故答案为: ①③④.
【点睛】此题主要考查了一次函数的图象,考查学生的分析能力和读图能力,一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0,函数y=kx+b的图象经过第二、三、四象限.
17.
【分析】根据点的坐标,得到,,进而得出蚂蚁爬行一圈的长度为个单位,再根据,得出所处位置为边中点,即可得到坐标.
【详解】解:点的坐标为,C点的坐标为,D点的坐标为,
,,
长方形,
,,
蚂蚁从点出发,爬行一圈的长度为,
,
又,,
蚂蚁爬行了个单位长度时,它所处位置为边中点,
坐标为,
故答案为:.
【点睛】本题考查了坐标与图形,两点的距离公式,利用数形结合的思想解决问题是解题关键.
18.(1);(2)该公司购买辆中型客车,辆大型客车时最省钱.
【分析】(1)根据购车的数量以及价格根据总费用直接表示出等式;
(2)根据购买中型客车的数量不超过12辆,得出,中x的取值范围,再根据y随着x的增大而减小,得出x的值.
【详解】解:(1)与的函数关系式为:;
(2)∵,
∴,
∴的值随的增大而减小.
∵,
∴当时,的值最小,
∴该公司购买辆中型客车,辆大型客车时最省钱.
【点睛】此题主要考查了一次函数的应用以及增减性,得出x取值范围再利用增减性得出x的值是解决问题的关键.
19.见解析
【分析】
(1)根据题中的计数方法即可得到结果;
(2)根据题意列出算式,计算即可得到结果;
(3)在图形中找出的位置,根据题意列出算式,计算即可得到结果;
(4)由,,得到到的过程,即可确定出.
【详解】
解:(1)根据题意得:图中,,;
(2)根据题意得:;
(3)如图所示,为甲虫子走过的路程为,
则甲虫从走到的过程中共需要消耗的能量为(焦耳);
(4)由,,
得到向右2个单位,向上3个单位到达,即应记为,
故答案为:(1);;;0;;;(4)
【点睛】此题考查了有理数的加减混合运算,正数与负数,解题的关键是正确的理解从一个点到另一个点移动时,如何用坐标表示.
20.(1)m>﹣3;(2)m=4.
【详解】试题分析:(1)直接利用一次函数的增减性得出m的取值范围;
(2)直接利用正比例函数的定义得出m的值.
解:(1)∵一次函数y=(m+3)x+m﹣4,y随x的增大而增大,
∴m+3>0,
解得:m>﹣3;
(2)∵y=(m+3)x+m﹣4是正比例函数,
∴m﹣4=0,
解得:m=4.
21.(1)20
(2)从第4分钟到第8分钟
【分析】(1)用待定系数法求出直线BC的解析式,然后求出C点坐标即可;
(2)分别计算AB段和BC的速度作比较即可得出结论.
【详解】(1)解:设直线BC的解析式为y=kx+b,
代入点(5,6)和(10,4)
得,
解得:,
∴直线BC的解析式为,
当y=0时,x=20,
故答案为:20;
(2)由题知:
AB段的速度为:(12-6)÷5=1.2(km/min),
BC段的速度为:(6-4)÷(10-5)=0.4(km/min),
4分钟行驶了2.4千米的平均速度为:2.4÷4=0.6(km/min),
则小明爸爸连续的四分钟有一段在AB段有一段在BC段,
设在AB段行驶时间为x min,则在BC段行驶(4-x)min,
由题意得1.2x+(4-x)×0.4=2.4,
解得x=1,
5-1=4(min),4+4=8(min),
∴这4分钟的起止时间是从第4分钟到第8分钟.
【点睛】本题主要考查一次函数的应用,熟练掌握待定系数法求一次函数是解题的关键.
22.走法一:(3,1)→(6,1)→(6,2)→(7,2)→(8,2)→(8,5);走法二:(3,1)→(3,2)→(3,5)→(4,5)→(7,5)→(8,5).(答案不唯一).这几种走法的路程相等.
【分析】根据题意,走法有多种,只要符合只能向上或向右走即可,通过走的路径可判断这些走法的路程相等.
【详解】
走法一:(3,1)→(6,1)→(6,2)→(7,2)→(8,2)→(8,5);
走法二:(3,1)→(3,2)→(3,5)→(4,5)→(7,5)→(8,5).(答案不唯一).
这几种走法的路程相等.
【点睛】本题考查了坐标确定位置:平面直角坐标系中点与有序实数对一一对应.
23.(1)
(2)
(3)学校共有两种租车方案,最少费用为元
【分析】本题主要考查了一元一次方程的实际应用,一元一次不等式组的实际应用,一次函数的实际应用,解题的关键是正确理解题意,根据题意找出数量关系,列出方程、不等式组、一次函数表达式.
(1)设参加本次实践活动的老师有名,根据“若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生”列出方程求解即可;
(2)根据题意列函数关系式即可;
(3)根据题意列不等式,求解不等式,然后根据随的增大而增大,求解即可;
【详解】(1)解:设老师有名,学生有名,
根据题意,得解得,
老师有名,学生有名;
每辆车上至少有名老师,
汽车总数不能大于辆,
,
要保证名师生有车坐,汽车总数不能少于(取整数)辆,
共需租车辆.
(2);
(3)学校在租车总费用元的限额内,租用汽车送师生返校,
,
,即.
,
要保证名师生有车坐,
,
,
,
有两种租车方案:
方案一:租辆甲型客车,辆乙型客车;
方案二:租辆甲型客车,辆乙型客车;
,
随的增大而增大,
当时,y最小,.
答:学校共有两种租车方案,最少费用为元.
24.(1),
(2)点B坐标为,点C坐标为
(3)
(4)存在,点P坐标为或或或
【分析】(1)待定系数法求出m,n的值即可;
(2)令,分别求出相应的函数值和自变量,即可得出结果;
(3)结合图象法,即可得出结论;
(4)分三边两两相等,三种情况,进行讨论求解即可.
【详解】(1)正比例函数的图象过点.
,
.
又一次函数的图象过点
,
.
(2)解:由(1)可得,一次函数的解析式为,
令,则
,
点B坐标为,
令,则,
点C坐标为;
(3)解:由图象可知:在A点右侧,函数的值小于函数的值;
故;
(4)存在,点P坐标为或或或.
点,
,
当时,且点P在x轴上,
则点或;
当时,如图,过点A作于E,
则点,
,,
,
点;
当时,
,
,
点,
综上所述:点P坐标为或或或.
【点睛】本题考查一次函数的综合应用.正确的求出函数解析式,利用数形结合和分类讨论的思想,进行求解,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
