14.1 函数 同步练习（含解析）

中小学教育资源及组卷应用平台
14.1函数
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列关于变量x，y的关系中，y不是x的函数的是（　　）
A． B．
C． D．
2．汽车油箱中有汽油，如果不再加油，油箱中的油量y（单位：L）随行驶路程x（单位：）的增加而减少，平均耗油量为．当时，y与x之间的关系式是（ ）
A． B．
C． D．
3．数学兴趣小组用同一块木板，测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间，支撑物高度与小车下滑时间之间的关系如下表所示：
支撑物高度 10 20 30 40 50 60 70
小车下滑时间 4.23 3.00 2.45 2.13 1.89 1.71 1.59
根据表格提供的信息，下列说法错误的是（ ）
A．支撑物高度为时，小车下滑时间为
B．支撑物高度越大，小车下滑时间越小
C．若小车下滑时间为，则支撑物高度在至之间
D．若支撑物高度为，则小车下滑时间可以小于的任意值
4．若长方形的周长为，其中一边为，面积为，则这样的长方形中y与x的关系可以写为（ ）
A． B． C． D．
5．下列关系式中，y不是x的函数的是（ ）
A． B． C． D．
6．声音在空气中传播的速度简称音速，实验测得音速气温的一些数据如表：下列结论错误的是（ ）
气温x（） 0 5 10 15 20
音速y（米/秒） 331 334 337 340 343
A．在变化中，气温是自变量，音速是因变量 B．y随x的增大而增大
C．当气温为时，音速为343米/秒 D．温度每升高，音速增加3米/秒
7．函数叫做高斯函数，其中x为任意实数，表示不超过x的最大整数．定义，则下列说法正确的个数为( )
①；
②；
③高斯函数中，当时，x的取值范围是；
④函数中，当时，．
A．0 B．1 C．2 D．3
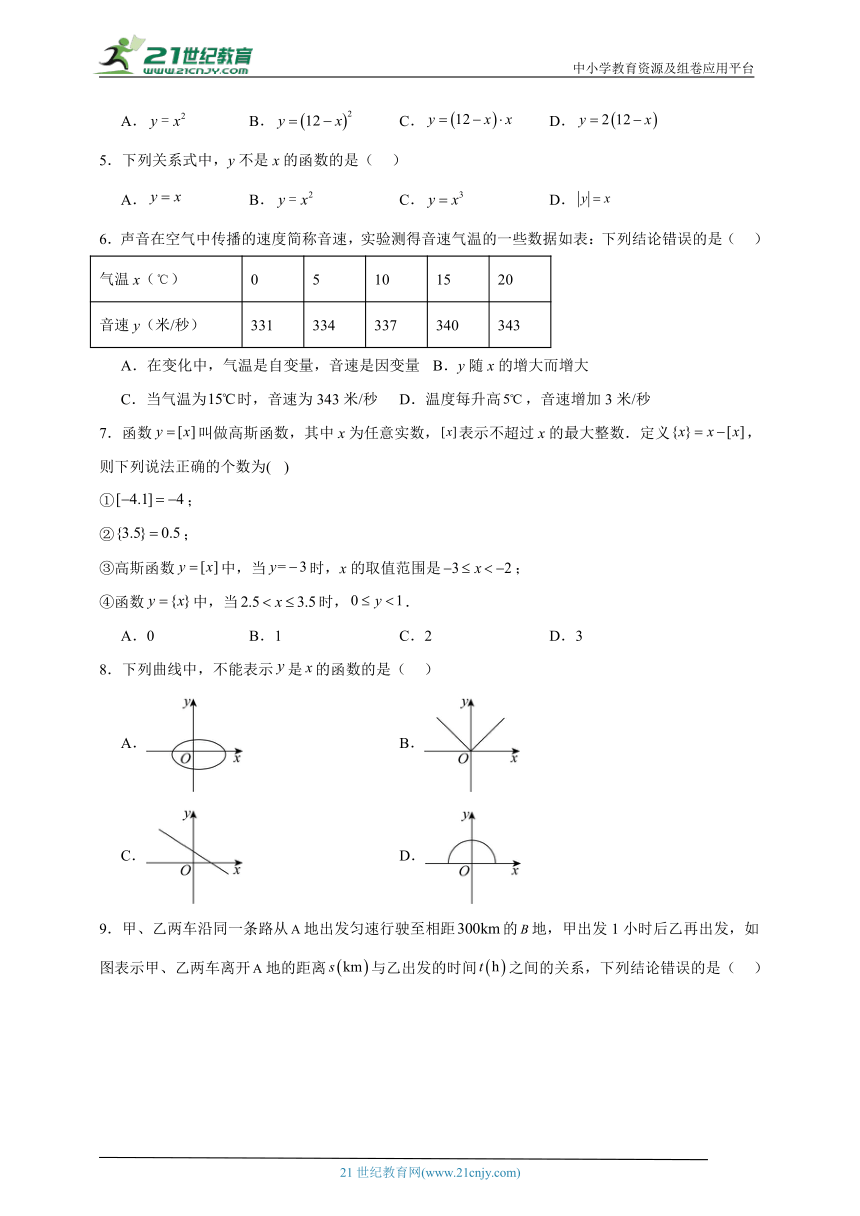
8．下列曲线中，不能表示是的函数的是（ ）
A． B．
C． D．
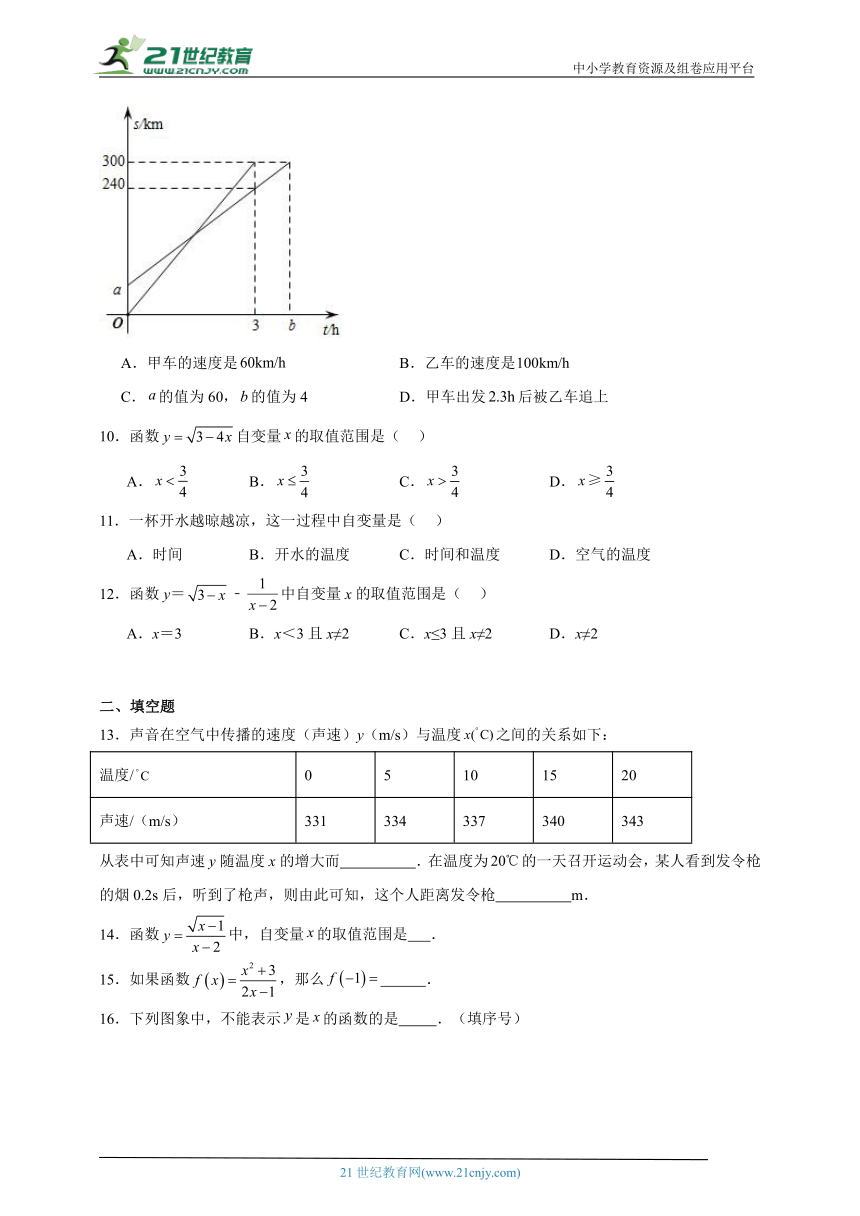
9．甲、乙两车沿同一条路从地出发匀速行驶至相距的地，甲出发1小时后乙再出发，如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系，下列结论错误的是（ ）
A．甲车的速度是 B．乙车的速度是
C．的值为60，的值为4 D．甲车出发后被乙车追上
10．函数自变量的取值范围是（ ）
A． B． C． D．
11．一杯开水越晾越凉，这一过程中自变量是（ ）
A．时间 B．开水的温度 C．时间和温度 D．空气的温度
12．函数y＝﹣中自变量x的取值范围是（ ）
A．x＝3 B．x＜3且x≠2 C．x≤3且x≠2 D．x≠2
二、填空题
13．声音在空气中传播的速度（声速）y（m/s）与温度之间的关系如下：
温度/ 0 5 10 15 20
声速/（m/s） 331 334 337 340 343
从表中可知声速y随温度x的增大而 ．在温度为的一天召开运动会，某人看到发令枪的烟0.2s后，听到了枪声，则由此可知，这个人距离发令枪 m．
14．函数中，自变量的取值范围是 ．
15．如果函数，那么 ．
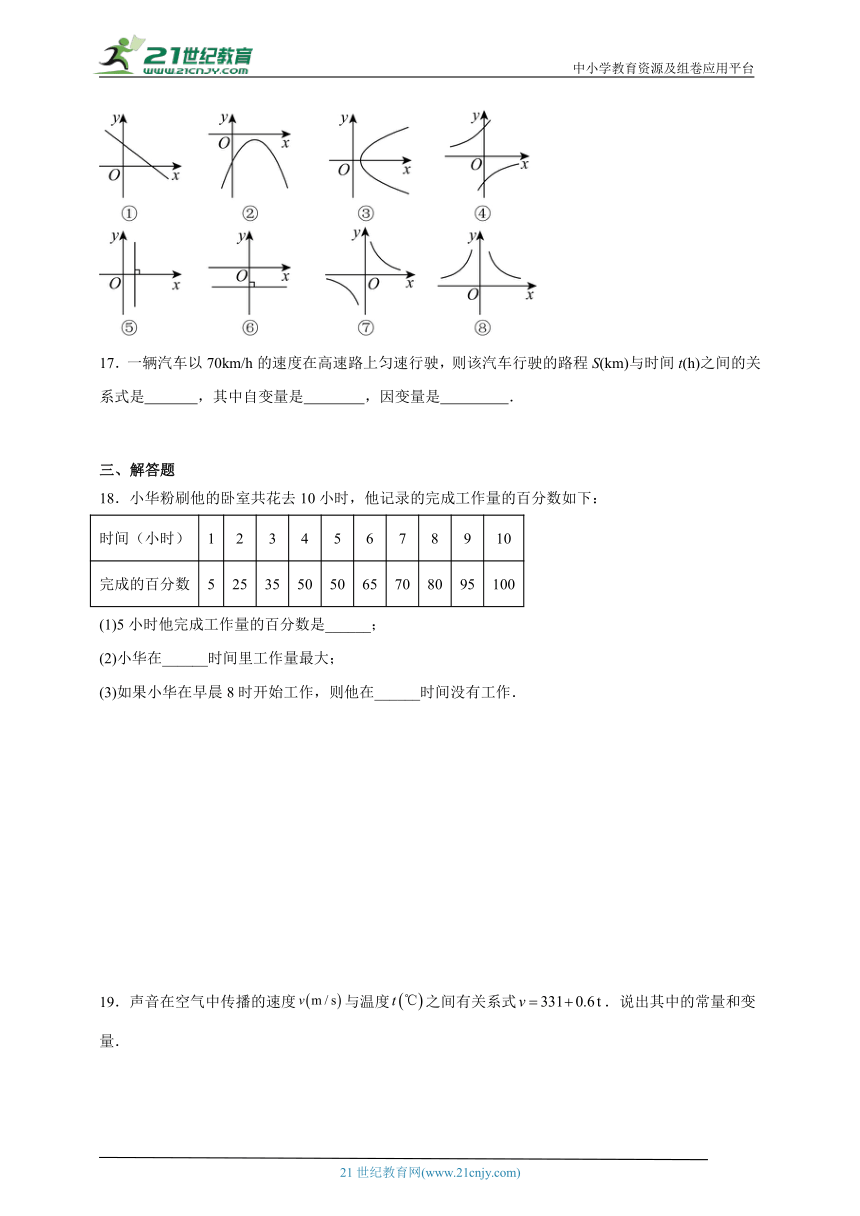
16．下列图象中，不能表示是的函数的是 ．（填序号）
17．一辆汽车以70km/h的速度在高速路上匀速行驶，则该汽车行驶的路程S(km)与时间t(h)之间的关系式是 ，其中自变量是 ，因变量是 ．
三、解答题
18．小华粉刷他的卧室共花去10小时，他记录的完成工作量的百分数如下：
时间（小时） 1 2 3 4 5 6 7 8 9 10
完成的百分数 5 25 35 50 50 65 70 80 95 100
(1)5小时他完成工作量的百分数是______；
(2)小华在______时间里工作量最大；
(3)如果小华在早晨8时开始工作，则他在______时间没有工作．
19．声音在空气中传播的速度与温度之间有关系式．说出其中的常量和变量．
20．在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，如表是测得的弹簧的长度与所挂物体的质量的几组对应值：
所挂物体质量 0 1 2 3 4
弹簧长度 16 18 20 22 24
(1)在这个表格中反映的是________和_________两个变量之间的关系：_________是自变量，_________是因变量；
(2)弹簧长度与所挂物体质量的关系式是_________；
(3)若弹簧的长度为时，此时所挂重物的质量是多少？（在弹簧的允许范围内）
21．如图所示，分别表示了香蕉、苹果的总价与数量之间的关系，看图回答问题．
(1)香蕉的总价和数量成______比例关系；（填“正”或“反”）
(2)从图象上看，单价更贵一些的水果是______；
(3)买x千克苹果要用______元，y元可以买_____千克香蕉．
22．我市通过“互联网+”“大数据”等新科技，打造“智慧停车平台”，着力化解城市“停车难”问题．市内某智慧公共停车场的收费标准是停车不超过30分钟，不收费；超过30分钟，不超过60分钟，计1小时，收费3元；超过1小时后，超过1小时的部分按每小时2元收费（不足1小时，按1小时计）．
(1)若张先生某次在该停车场停车2小时10分钟，应交停车费　 　元；若李先生也在该停车场停车，并支付了11元停车费，则该停车场是按　 　小时（填整数）计时收费．
(2)当x取整数且x≥1时，求该停车场停车费y（元）关于停车计时x（小时）的函数解析式．
23．已知中，，矩形的长和宽分别为9cm和2cm，点P和点A重合，和在同一条直线上（如图所示），不动，矩形沿射线以每秒1cm的速度向右移动，设移动后，矩形与重叠部分的面积为，求y与x之间的函数关系式．
24．小明某天上午9时骑自行车离开家，15时回到家，他描绘了离家的距离与时间的变化情况，如下图所示．
图象表示了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
《14.1函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D C D C D A D B
题号 11 12
答案 A C
1．D
【分析】根据函数的定义进行判断即可．
【详解】解：A、对于的每一个确定的值，都有唯一确定的值与其对应，所以是的函数，此项不符题意；
B、对于的每一个确定的值，都有唯一确定的值与其对应，所以是的函数，此项不符题意；
C、对于的每一个确定的值，都有唯一确定的值与其对应，所以是的函数，此项不符题意；
D、当或时，有两个的值与其对应，所以不是的函数，此项符合题意；
故选：D．
【点睛】本题考查了函数的定义．解题的关键在于熟练掌握：一般地，在一个变化过程中，如果有两个变量与，并且对于的每一个确定的值，都有唯一确定的值与其对应，那么我们就说是自变量，是的函数．
2．B
【分析】此题主要考查了根据实际问题列变量间的表达式以及自变量取值范围求法，正确得出x、y的表达式是解题关键．直接利用油箱中的油量y=总油量-耗油量进而得出x与y的关系式，再求出x的求值范围，即可得出答案．
【详解】解：由题意可知：，
故选：B．
3．D
【分析】根据函数的表示方法对各选项进行逐一分析即可．
【详解】解：A、由表可知，当h=40cm时，t=2.13s，故A正确；
B、支撑物高度h越大，小车下滑时间t越小，故B正确；
C、若小车下滑时间为2s，则支撑物高度在40cm至50cm之间，故C正确；
D、若支撑物的高度为80cm，则小车下滑时间可以是小于1.59s，但不是任意值，故D错误．
故选：D．
【点睛】本题考查了函数的表示方法，观察表格获得信息是解题关键．
4．C
【分析】由长方形的周长为和其中一边为，可求出长方形的另一边为，进而由长方形的面积公式可求出．
【详解】解：∵长方形的周长为，其中一边为，
∴长方形的另一边为，
∴该长方形的面积为，即．
故选：C．
【点睛】本题考查列代数式．理解题意，掌握长方形的周长和面积公式是解题关键．
5．D
【分析】根据对于x的每一个确定的值，y是否有唯一的值与其对应进行判断．
【详解】解：A、，y是x的函数，故A不符合题意；
B、，y是x的函数，故B不符合题意；
C、，y是x的函数，故C不符合题意；
D、，当时，，即对于x的每一个确定的值，y不是有唯一的值与其对应，
∴y不是x的函数，故D符合题意．
故选：D．
【点睛】本题考查的是函数的定义，设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数．
6．C
【分析】根据表格中的数据以及函数的定义，逐一判断选项即可．
【详解】A、∵对于气温的每一个值，都存在一个唯一确定的音速，符合函数定义，
∴气温是自变量，音速是因变量，正确，
∴A不符合题意；
B、由表格数据可知：y随x的增大而增大，
∴B不符合题意；
C、由表格数据可知：当气温为15°C时，音速为340米/秒，错误，
∴C符合题意；
D、由表格数据可知：温度每升高5°C，音速增加 3米/秒，正确，
∴D不符合题意．
故选：C．
【点睛】本题主要考查了函数的表示方法，掌握函数的定义，得出温度每升高5°C，音速增加 3米/秒，是解题关键．
7．D
【分析】根据表示不超过x的最大整数，即可解答．
【详解】解：①，故原说法错误；
②，正确，符合题意；
③高斯函数中，当时，x的取值范围是，正确，符合题意；
④函数中，当时，，正确，符合题意；
所以，正确的结论有3个．
故选：D．
【点睛】本题考查了有理数的混合运算，解决本题的关键是明确表示不超过x的最大整数．
8．A
【分析】本题考查函数的概念，关键是掌握函数的定义．
设在一个变化过程中有两个变量与，对于的每一个确定的值，都有唯一的值与其对应，那么就说是的函数，由此即可判断．
【详解】解：A、不符合函数的定义，不是的函数，故此选项符合题意；
B、符合函数的定义，是的函数，故此选项不符合题意；
C、符合函数的定义，是的函数，故此选项不符合题意；
D、符合函数的定义，是的函数，故此选项不符合题意；
故选：A．
9．D
【分析】根据图象，列出关于a，b的方程，求出a，b的值，从而即可逐一判断各个选项．
【详解】解：根据图象可知，（300-a）÷b=（240-a）÷3=a÷1，
解得：a=60，b=4，
甲车的速度=60÷1=60km/h，乙车的速度=300÷3=100km/h，
故A，B，C正确，不符合题意；
∵60÷（100-60）=1.5，1.5+1=2.5h，
∴甲车出发后被乙车追上，
故D错误，符合题意，
故选D．
【点睛】本题考查了用图像表示的变量间关系，理解图象以及分别求出甲、乙两人的速度是解题的关键．
10．B
【分析】根据二次根式有意义的条件，被开方数大于等于0，即可得到答案．
【详解】解：由题可得：，
∴．
故选：B．
【点睛】本题考查二次根式的定义及相关基础问题，熟练掌握二次根式有意义的条件是解题的关键．
11．A
【分析】在研究过程中，变化的量叫做自变量，据此解答即可．
【详解】解：∵开水的温度随着时间会逐渐降低，
∴在这一过程中，自变量是时间，
故选：A．
【点睛】本题考查自变量的定义．熟记定义即可．
12．C
【分析】根据被开方数是非负数，分母不能为零列不等式组求解．
【详解】解：由题意得： 3﹣x≥0且x﹣2≠0，
解得：x≤3且x≠2．
故选：C．
【点睛】本题主要考查了函数自变量的取值范围，根据被开方数是非负数、分母不能为零列出不等式组是解答本题的关键．
13． 增大
【分析】从表格可以看到随的增大而增大；时，音速为343米秒，距离为米．
【详解】解：从表格可以看到随的增大而增大，
时，音速为343米秒，
米，
这个人距离发令点米．
故答案为：增大，．
【点睛】本题考查变量之间的关系，能够通过表格观察出变量的变化关系，利用表格的数据计算距离是解题的关键．
14．且
【分析】根据分式有意义的条件：分母不为0以及二次根式有意义的条件：被开方数不小于0进行解答即可．
【详解】解：由题意得且，即且，
故答案为：且．
【点睛】本题考查了函数自变量的取值范围问题，掌握分式有意义的条件以及二次根式有意义的条件是解题的关键．
15．
【分析】把代入函数即可求解．
【详解】解：∵，
∴
．
故答案为：．
【点睛】此题主要考查函数值求解，解题的关键是把自变量的值代入函数解析式．
16．③④⑤
【分析】本题考查函数定义，解题的关键是理解掌握自变量x在一定的范围内取一个值，因变量y有唯一确定的值与之对应，则y叫x的函数．根据函数的定义，自变量x在一定的范围内取一个值，因变量y有唯一确定的值与之对应，则y叫x的函数，即可得出答案．
【详解】解：根据函数的定义可知，③和④部分自变量x在一定的范围内取一个值，因变量y有俩个确定的值与之对应，⑤自变量x在一定的范围内取一个值，因变量y有无数个的值与之对应，不满足函数定义．其余均满足函数的定义即自变量x在一定的范围内取一个值，因变量y有唯一确定的值与之对应，．
故答案为：③④⑤．
17． t S
【分析】根据题意进行求解即可；
【详解】解：∵路程=速度×时间，
∴
∵行驶路程随着时间的增加而增加，
∴自变量是t（或时间）；因变量是S（或汽车行驶的路程）；
故答案为：；t；S．
【点睛】本题主要考查变量间的关系，掌握路程=速度×时间是解本题的关键．
18．(1)
(2)第二小时
(3)时
【分析】本题考查了函数的表示方法，比较简单，阅读图表数据，准确获取信息是解题的关键．
（1）根据图表数据解答即可；
（2）根据数据找出完成百分数最多的时间即可；
（3）根据完成的百分数，开始工作后4到5小时没有工作，然后求出相应的时间即可．
【详解】（1）5小时他完成工作量的百分数是；
故答案为：；
（2）由图表可知，在第二小时完成的百分数最大是，所以，在第二小时时间里工作量最大；
故答案为：第二小时；
（3）开始工作小时工作量都是没有发生变化，
早晨8时开始工作，
在时时间没有工作．
故答案为：时．
19．常量为，变量为速度与温度
【分析】一般地，在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有为一得值与其对应，那么我们就说x是自变量，所以上述过程中，自变量是时间．
【详解】解：根据题意得：常量为，变量为速度与温度．
【点睛】本题主要考查了常量与变量问题，熟练掌握常量与变量必须存在于同一个变化过程中，判断一个量是常量还是变量，需要看两个方面：一是它是否在一个变化过程中；二是看它在这个变化过程中的取值情况是否发生变化是解题的关键．
20．(1)所挂物体质量，弹簧长度；所挂物体质量；弹簧长度；
(2)
(3)5.5kg
【分析】（1）根据表格标注的内容解答即可；
（2）由表格可知，物体每增加1千克，弹簧长度增加，据此即可写出弹簧长度与所挂物体质量的关系式；
（3）把代入（2）中关系式计算即可．
【详解】（1）解：上表反映了弹簧长度与所挂物体质量之间的关系；其中所挂物体质量是自变量，弹簧长度是因变量；
故答案为：所挂物体质量，弹簧长度；所挂物体质量；弹簧长度；
（2）解：物体每增加1千克，弹簧长度增加，
；
（3）解：把代入，
得，
解得：．
因此，此时所挂重物的质量是．
【点睛】本题考查了自变量与因变量的意义，以及用函数关系式表示变量间的关系，根据题意正确写出函数关系式是解题的关键．
21．(1)正
(2)香蕉
(3)4x，
【分析】此题考查了正比例和反比例的判断，并从图中获取数据，进行计算．
（1）正比例：如果两种相关联的量中相对应的两个数的比值一定，这两种量就叫做成正比例的量．它们的关系叫做正比例关系；反比例：如果两个变量的乘积为常数时的比例关系，一方发生变化，其另一方随之起相反的变化，就是反比例．
（2）从图中获得数据，香蕉的单价高于苹果的单价．
（3）单价数量总价，总价单价数量，代入即可．
【详解】（1）从图中可以看出，香蕉的总价和购买的数量成正比例；
（2）从图象上看，单价更贵一些的水果是香蕉；
（3）从图象上看，买1千克苹果要用4元，买1千克香蕉要用8元，
买x千克苹果要用元，y元可以买千克香蕉；
故答案为：，．
22．(1)7；5
(2)y＝2x+1
【分析】（1）根据题意可知，停车2小时10分钟，则超出1小时的部分以2小时计算；支付停车费11元，则超出时间为（11﹣3）÷2＝4（小时），故停车场按5小时计时收费；
（2）根据题意即可得出停车场停车费关于停车计时x（单位：小时）的函数关系式．
【详解】（1）解：若张先生某次在该停车场停车2小时10分钟，应交停车费为：3+2×2＝7（元）；
若李先生也在该停车场停车，支付停车费11元，则超出时间为（11﹣3）÷2＝4（小时），
∴停车场按5小时计时收费的．
故答案为：7；5；
（2）当停车计时x（单位：小时）取整数且x≥1时，此时需缴停车费为y＝3+2（x﹣1）＝2x+1．
答：停车场停车费y（元）关于停车计时x（小时）的函数解析式为y＝2x+1．
【点睛】本题考查的是分段收费的理解，有理数的混合运算的实际应用，列一次函数的关系式，理解题意，正确列式计算与列函数关系式是解本题的关键.
23．
【分析】分图1，图2，图3三种情况，利用三角形面积公式和梯形面积公式进行讨论求解即可．
【详解】运动过程中，重叠部分图形的形状在发生改变，重叠部分面积也随之而变化，由此可知题目需进行以下分类讨论：
当时，如图1所示，重叠部分为等腰直角三角形，腰长为，得：；
当时，如图2所示，重叠部分为直角梯形，梯形高即为矩形宽为，梯形下底长为，上底长为，得：；
当时，如图3所示，重叠部分为直角梯形，梯形高即为矩形宽为，梯形下底长即为等腰直角三角形腰长保持不变，则上底长为，得保持不变．
综上所述，
【点睛】本题主要考查了求函数关系式，掌握矩形的性质，等腰直角三角形的性质，利用分类讨论的思想求解是解题的关键．
24．图象表示了离家的距离与时间这两个变量之间的关系，其中时间是自变量，离家的距离是因变量．
【分析】此题考查了从函数图象获取信息．从函数图象即可得到图象表示了离家的距离与时间这两个变量之间的关系，其中时间是自变量，离家的距离是因变量．
【详解】解：图象表示了离家的距离与时间这两个变量之间的关系，其中时间是自变量，离家的距离是因变量．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)