14.3 函数图象的画法 同步练习(含解析)
文档属性
| 名称 | 14.3 函数图象的画法 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
14.3函数图像的画法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用恒定不变的水速往某一容器里注水,该容器的水位高度h(dm)与注水时间t(min)的关系如图,则该容器的形状可能是( )
A. B. C. D.
2.下列曲线中不能表示y是x的函数的是( )
A. B. C. D.
3.如图是雷达探测器在一次探测中发现的五个目标,若记图中目标C的位置为,则点E的位置为( )
A. B. C. D.
4.小敏家在学校正南方向,正东方向处.若以学校所在位置为原点,以正北、正东为正方向,则小敏家用有序数对规定:东西方向在前,南北方向在后表示为( )
A. B.
C. D.
5.如图,学校(记作A)在爱棣家(记作B)西偏南的方向上,且与爱棣家的距离是,若,且,则超市(记作C)在爱棣家的( )
A.南偏东的方向上,相距 B.南偏东的方向上,相距
C.南偏东的方向上,相距 D.东偏南的方向上,相距
6.如图是雷达探测到的6个目标,若目标B用表示,目标D用表示,那么表示的是目标( )
A.F点 B.E点 C.A点 D.C点
7.下列表述中,能确定物体位置的是( )
A.万达影城1号厅2排 B.温泉南路
C.南偏西 D.东经,北纬
8.在某游乐场,以中心广场为观测点,若有序数对表示图中“太阳神车”的位置,有序数对表示图中“雪域金翅”的位置,则与图中“天地双雄”位置对应的有序数对为( )
A. B. C. D.
9.在平面内,下列数据不能确定物体位置的是( )
A.南偏西方向 B.某小区3座406室
C.东经,北纬 D.电影院3排4座
10.平面直角坐标系中,点,,经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( ).
A. B. C. D.
11.在平面直角坐标系中,若点在第二象限,则m可能是( )
A. B.0 C. D.2
12.已知点在第二象限,且点P到x轴的距离与到y轴的距离之和是11,则a的值为( )
A. B.1 C. D.3
二、填空题
13.如图,在平面直角坐标系中,点A(0,4)在y轴正半轴上,点B(-3,0)在x轴负半轴上,且AB=5,点M坐标为(3,0),N点为线段OA上一动点,P为线段AB上的一动点,则MN+NP的最小值为 .
14.已知点的坐标为,且点在轴上,则的值为 .
15.平面直角坐标系xOy中,已知点P(m,m+2),点Q(n,0),点M(1,1),则PQ+QM最小值为 .
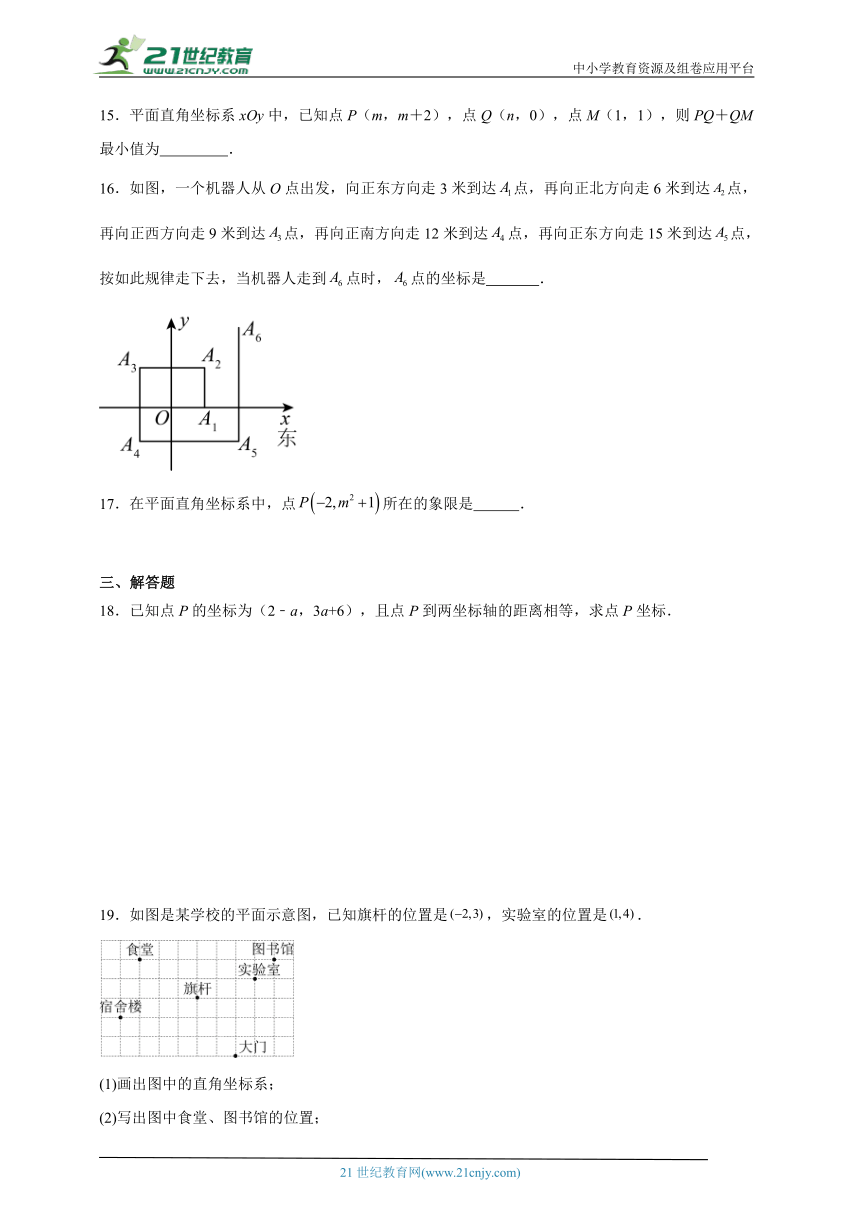
16.如图,一个机器人从O点出发,向正东方向走3米到达点,再向正北方向走6米到达点,再向正西方向走9米到达点,再向正南方向走12米到达点,再向正东方向走15米到达点,按如此规律走下去,当机器人走到点时,点的坐标是 .
17.在平面直角坐标系中,点所在的象限是 .
三、解答题
18.已知点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,求点P坐标.
19.如图是某学校的平面示意图,已知旗杆的位置是,实验室的位置是.
(1)画出图中的直角坐标系;
(2)写出图中食堂、图书馆的位置;
(3)已知办公楼的位置是,教学楼的位置是,在图中标出办公楼和教学楼的位置;
(4)如果一个单位长度表示30米,请求出宿舍楼到教学楼的实际距离.
20.如图,已知图中点和点的坐标分别为和.
(1)请在图中画出坐标轴建立适当的直角坐标系;
(2)写出点的坐标为________;
(3)连接、和得,在轴的负半轴有点满足,则点的坐标为________,________个平方单位;
21.嘉嘉从A处出发向北偏东走了30m,到达B处;淇淇从A处出发向南偏东走了40m,到达C处.
(1)用1cm表示10m,画图表示A,B,C的位置;
(2)A处在C处的______偏______度的方向上,距离C处______米;
(3)叙述A处相对于B处的位置.
22.哥哥从家里骑自行车出发,去超市途中遇到妹妹从超市走路回家,哥哥在超市买完东西后以原先速度骑车回家,在回去的路上又遇到了妹妹,便载妹妹一起回家,结果哥哥比按原先速度回家的时间晚了3分钟,二人离超市的距离和哥哥从家出发后的时间之间的关系如图所示(假设二人交流时间忽略不计).
(1)家与超市相距________;
(2)哥哥和妹妹第1次相遇时离超市的距离是多少?
(3)哥哥从家里出发到回家所用的时间是多少?
23.学校举行大型活动,用甲、乙两架无人机进行航拍,若无人机在上升过程中匀速飞行,甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,无人机所在高度(米)与时间(秒)之间的关系如图所示,根据图象回答下列问题:
(1)甲在空中停留时的高度是______米,甲出发______秒后乙开始起飞,点表示的意义是_________;
(2)甲、乙两架无人机的上升速度分别是多少米/秒?
(3)当时,两架无人机所在的高度相差多少米?
24.6月13日,某港口的潮水高度y()和时间x(h)的部分数据及函数图像如下:
x(h) … 11 12 13 14 15 16 17 18 …
y() … 189 137 103 80 101 133 202 260 …
(数据来自某海洋研究所)
(1)数学活动:
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图像.
②观察函数图像,当时,y的值为多少?当y的值最大时,x的值为多少?
(2)数学思考:
请结合函数图像,写出该函数的两条性质或结论.
(3)数学应用:
根据研究,当潮水高度超过260时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?
《14.3函数图像的画法》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C B D D B A D
题号 11 12
答案 D C
1.D
【分析】本题考查利用函数图象表示变量之间的关系,从图象可知,相同注水速度下,水面上升的速度随着注水时间的增加而减小,即可得出结论.
【详解】解:图象可知,相同注水速度下,水面上升的速度随着注水时间的增加而减小,
∴容器的形状可能是下窄上宽,
故选D.
2.C
【分析】根据函数的定义,对于x的每一个确定的值,y都有唯一的值与其对应,确定正确的选项.
【详解】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故B不符合题意;
C、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故C符合题意;
D、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故D不符合题意;
故选:C.
【点睛】本题考查了函数的定义,掌握函数的定义是解题关键.
3.C
【分析】根据度数表示纵坐标,圆圈数表示横坐标,可得答案.
【详解】解:因为记图中目标C的位置为,
所以点E的位置为.
故选:C
【点睛】此题主要考查了坐标确定位置,正确理解题意得出横纵坐标的意义是解题关键.
4.C
【分析】本题考查了坐标确定位置,根据题意可得到点的坐标,正确掌握点的坐标是解题的关键.
【详解】解:∵小敏家在学校正南方向,正东方向处,
∴横坐标为200,纵坐标为,
∴点的坐标为,
故选:C.
5.B
【分析】根据方向角的定义即可解答.
【详解】解:∵A在B西偏南的方向上,,
∴C在B的南偏东的方向上,
∵,,
∴km,
∴超市(记作C)在爱棣家的南偏东的方向上,相距.
故选:B.
【点睛】本题考查了方向角,根据题目的已知条件并结合图形分析是解题的关键.
6.D
【分析】本题考查了坐标位置的确定,根据位置的表示方法,第一个数表示距观察站的圈数,第二个数表示度数写出即可.
【详解】解:∵目标B用表示,目标D用表示,
∴第一个数表示距观察站的圈数,第二个数表示度数,
∴表示为的目标是:C.
故选:D.
7.D
【分析】根据确定位置的有序数对有两个数解答.
【详解】解:在平面直角坐标系中,要用两个数据才能表示一个点的位置,纵观各选项,只有东经,北纬能确定物体的位置,
故选:D
【点睛】本题考查了坐标确定位置,理解在平面直角坐标系中,要用两个数据才能表示一个点的位置是解题的关键.
8.B
【分析】根据“太阳神车”与“雪域金翅”的位置结果找到位置的表示方法,即可求解.
【详解】∵“太阳神车”的位置为(500,20°),“雪域金翅”的位置为(400,340°),
∴可知有序数对的第一个值为:目标距离观测点中心广场的距离,第二个值为:目标与观测点中心广场的连线与正东方向的旋转角度度数,
∴根据图形可知,“天地双雄”距离观测点中心广场的距离为:500,天地双雄”与观测点中心广场的连线与正东方向的旋转角度度数为120°,
即有序数对为(500,120°),
故选:B.
【点睛】本题考查了用有序数对表示位置的知识,理解题意是解答本题的关键.
9.A
【分析】本题考查了确定位置,解题的关键是根据坐标确定位置需要两个数据,对各选项分析判断后求解.
【详解】解:A、南偏西方向,无法确定物体的具体位置,故本选项符合题意;
B、某小区3座406室,位置明确,故本选项不符合题意;
C、东经,北纬,位置明确,故本选项不符合题意;
D、电影院3排4座,位置明确,故本选项不符合题意.
故选:A.
10.D
【分析】根据题意画出图形,根据直线a//x轴,得到直线a为直线y= 2,根据垂线段最短即可得出答案.
【详解】
如图,∵直线a// x轴,
∴直线a为直线y= 2,
当BC⊥a时,线段BC最短,
∴点C的坐标为(2, 2).
故选: D.
【点睛】本题考查了坐标与图形性质,掌握平行于x轴的坐标的特点,以及垂线段最短是解题的关键.
11.D
【分析】本题主要考查点所在象限,先根据第二象限内点的坐标符号特点确定m的正负,然后结合各选项即可解答.掌握第二象限的点的横坐标小于零、纵坐标大于零是解题的关键.
【详解】解:∵点在第二象限,
∴,
∴A、B、C选项不符合题意,D选项符合题意.
故选:D.
12.C
【分析】本题考查了坐标与图形的性质,熟练掌握第二象限的点的坐标特征是解题的关键.根据第二象限的点的坐标特征,得到,,再结合“点P到x轴的距离与到y轴的距离之和是11”,列出方程求出a的值即可解答.
【详解】解:点在第二象限,
,,
点P到x轴的距离为,到y轴的距离为,
由题意得,,
解得:.
故选:C.
13.
【分析】连接AM,根据点A(0,4),点B(-3,0),点M坐标为(3,0),得到OA=4,OB=3,OM=3,过M作MP⊥AB于P交OA于N,则此时,MN+NP的值最小,且MN+NP的最小值=MP,根据三角形的面积公式即可得到结论.
【详解】解:连接AM,
∵点A(0,4),点B(-3,0),点M坐标为(3,0),
∴OA=4,OB=3,OM=3,
过M作MP⊥AB于P交OA于N,
则此时,MN+NP的值最小,且MN+NP的最小值=MP,
∵, BM=6,OA=4,AB=5,
∴.
故答案为:.
【点睛】本题考查垂线段最短的应用,坐标与图形性质,三角形的面积公式,正确的作出图形是解题的关键.
14.
【分析】本题考查的是点的坐标,正确掌握相关性质内容是解题的关键.
根据轴上点的纵坐标等于0得出关于的方程,求出的值即可.
【详解】解:因为点的坐标为,且点在轴上,
,
解得,
故答案为:.
15.
【分析】根据点P(m,m+2)可知,点P在一次函数的图像上移动,作出图示,并作M关于x轴的对称点,过点作于点P,交x轴于点Q,连接,QM,利用“垂线段最短”原理,可知此时PQ+QM最小,最小值为的长度,利用等腰三角形的性质求解即可得出答案.
【详解】解:如图所示,由题意可知,点P(m,m+2)在一次函数的图像上移动, 一次函数分别交x轴、y轴于点A,B,作M关于x轴的对称点,过点作于点P,交x轴于点Q,连接,QM,利用“垂线段最短”原理,可知此时PQ+QM最小,最小值为的长.
点M(1,1),
由对称性质可知:点
一次函数的图像分别交x轴、y轴于点
令,解得,即点,令,解得,即点
为等腰三角形,
点P为AB的中点,则点
故答案为:
【点睛】本题考查了最值问题,涉及到一次函数的性质、等腰三角形的性质“三线合一”以及根据两点坐标求点之间的距离,思考问题时参照“将军饮马”模型,根据“垂线段最短”原理,将问题转化为求垂线段的长度是解决本题的关键.
16.
【分析】本题主要考查了坐标确定位置的运用,解题的关键是发现规律,利用规律解决问题,解题时注意:各象限内点的坐标特征为:第一象限:;第二象限:;第三象限:;第四象限:.
由于一个机器人从点出发,向正东方向走3米,到达点,那么点坐标为,再向正北走6米到达点,那么点坐标为,6),再向正西走9米到达点,那么点坐标为,然后依此类推,找出规律,即可求出的坐标.
【详解】解:根据题意可知:,
故点的坐标为;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
依此类推,可得点的坐标为,即.
故答案为:.
17.第二象限
【分析】本题考查判断点所在的象限,根据点的符号特征,进行判断即可.
【详解】解:∵,
∴,
∵,
∴点在第二象限,
故答案为:第二象限.
18.P点坐标为或
【分析】由题得,点P到两坐标轴的距离相等,则点P的横纵坐标绝对值相等,据此列式求解,即可得到a的值,进而确定点P的坐标;
【详解】解:∵点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,
∴|2-a|=|3a+6|,
化为:2-a=3a+6或2-a=-(3a+6),
解得a=-1或a=-4,
所以点P的坐标为(3,3)或(6,-6).
【点睛】本题主要考查了象限内点的坐标的特征,掌握象限内点的坐标的特征是解题的关键.
19.(1)见解析
(2)食堂、图书馆
(3)见解析
(4)
【分析】(1)根据旗杆的坐标可以得到原点的位置,建立平面直角坐标系即可;
(2)写出这两点的坐标即可;
(3)根据坐标,描出点的位置即可;
(4)宿舍楼到教学楼的距离是8个单位长度,乘以即可.
【详解】(1)解:直角坐标系如图所示;
(2)解:由图可知,食堂、图书馆;
(3)解:如图所示;
(4)解:由图可知宿舍楼到教学楼的实际距离为.
【点睛】本题考查了平面直角坐标系,点的坐标的表示方法,坐标确定位置,画出正确的平面直角坐标系是解题的关键.
20.(1)见解析
(2)
(3);
【分析】本题考查了直角坐标系、三角形的面积计算,能找到直角坐标系的原点、横纵坐标的正方向并画出直角坐标系是解答本题的关键.
(1)根据图中点和点的坐标确定原点的位置和横纵坐标的正方向即可得到答案;
(2)根据直角坐标的特点,即可写出的坐标;
(3)根据点在直角坐标系中的位置,先算出的面积,再根据三角形的面积公式即可算出答案.
【详解】(1)解:根据图中点和点的坐标确定原点的位置和横纵坐标的正方向,得到直角坐标系如下图:
(2)解:根据直角坐标系的特点,得到点的坐标为:,
故答案为:;
(3)解:画图如下:
根据点在直角坐标系中的位置,得到:,
假设点的坐标为,
,
又,
,
,
或,
在轴的负半轴,
,
故的坐标为,个平方单位,
故答案为:;.
21.(1)见解析
(2)北偏西,60,40
(3)A处在B处的南偏西30度,距离B处30米处
【分析】(1)确定比例尺为,图上1cm表示实际距离10m,明确方位角,画图;
(2)根据图形判断位置,A处在C处的北偏西度的方向上,距离C处40米;
(3)根据图形判断位置,A处在B处的南偏西30度,距离B处30米处;
【详解】(1)解:如图.
(2)解:A处在C处的北偏西度的方向上,距离C处40米;
(3)解:A处在B处的南偏西30度,距离B处30米处;
【点睛】本题考查比例尺,用方位角表示位置;理解方位角的表示方法是解题的关键.
22.(1)8
(2)4千米
(3)103分钟
【分析】本题考查了从函数图象中获取信息,采用数形结合的思想是解此题的关键.
(1)根据图象即可得出答案;
(2)先求出哥哥骑车的速度,根据图象,相遇时间为20分钟,计算即可得出哥哥和妹妹第1次相遇时离超市的距离;
(3)根据题意列式计算即可得出答案.
【详解】(1)解:由图可得:家与超市相距;
(2)解:由图可得:哥哥骑车的速度为:(千米/分钟),
根据图象,相遇时间为20分钟,
∴(千米),
∴哥哥和妹妹第1次相遇时离超市的距离是4千米;
(3)解:由题意得:(分钟).
∴哥哥从家里出发到回家所用的时间是103分钟.
23.(1),,秒时甲、乙无人机所在高度都是米
(2)甲、乙两架无人机的上升速度分别为4米/秒、6米/秒
(3)当时,两架无人机所在的高度相差米
【分析】(1)根据题意得,至时甲在空中停留,停留时的高度是米,根据甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞得甲出发秒后乙开始起飞,根据所给图象即可得点表示的意义;
(2)根据“速度=路程÷时间”进行计算即可得;
(3)根据速度、时间与路程的关系式列式进行计算即可得.
【详解】(1)解:根据题意得,至时甲在空中停留,停留时的高度是米,
∵甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,
∴甲出发秒后乙开始起飞,
点表示的意义是:秒时甲、乙无人机所在高度都是米,
故答案为:,,秒时甲、乙无人机所在高度都是米;
(2)解:甲架无人机的上升速度:,
乙架无人机的上升速度:,
答:甲、乙两架无人机的上升速度分别为4米/秒、6米/秒.
(3)解:,
答:当时,两架无人机所在的高度相差米.
【点睛】本题考查了图象问题,解题的关键是理解题意,根据所给图象获取信息,正确计算.
24.(1)①见解析;②,
(2)①当时,y随x的增大而增大;②当时,y有最小值80
(3)和
【分析】(1)①根据表格数据在函数图像上描点连线即可;
②根据函数图像估计即可;
(2)从增减性、最值等方面说明即可;
(3)根据图像找到y=260时所有的x值,再结合图像判断即可.
【详解】(1)①
②观察函数图像:
当时,;
当y的值最大时,;.
(2)答案不唯一.
①当时,y随x的增大而增大;
②当时,y有最小值80.
(3)根据图像可得:当潮水高度超过260时和,
【点睛】本题考查函数图像的画法、从函数图像获取信息,准确的画出函数图像是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
14.3函数图像的画法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用恒定不变的水速往某一容器里注水,该容器的水位高度h(dm)与注水时间t(min)的关系如图,则该容器的形状可能是( )
A. B. C. D.
2.下列曲线中不能表示y是x的函数的是( )
A. B. C. D.
3.如图是雷达探测器在一次探测中发现的五个目标,若记图中目标C的位置为,则点E的位置为( )
A. B. C. D.
4.小敏家在学校正南方向,正东方向处.若以学校所在位置为原点,以正北、正东为正方向,则小敏家用有序数对规定:东西方向在前,南北方向在后表示为( )
A. B.
C. D.
5.如图,学校(记作A)在爱棣家(记作B)西偏南的方向上,且与爱棣家的距离是,若,且,则超市(记作C)在爱棣家的( )
A.南偏东的方向上,相距 B.南偏东的方向上,相距
C.南偏东的方向上,相距 D.东偏南的方向上,相距
6.如图是雷达探测到的6个目标,若目标B用表示,目标D用表示,那么表示的是目标( )
A.F点 B.E点 C.A点 D.C点
7.下列表述中,能确定物体位置的是( )
A.万达影城1号厅2排 B.温泉南路
C.南偏西 D.东经,北纬
8.在某游乐场,以中心广场为观测点,若有序数对表示图中“太阳神车”的位置,有序数对表示图中“雪域金翅”的位置,则与图中“天地双雄”位置对应的有序数对为( )
A. B. C. D.
9.在平面内,下列数据不能确定物体位置的是( )
A.南偏西方向 B.某小区3座406室
C.东经,北纬 D.电影院3排4座
10.平面直角坐标系中,点,,经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( ).
A. B. C. D.
11.在平面直角坐标系中,若点在第二象限,则m可能是( )
A. B.0 C. D.2
12.已知点在第二象限,且点P到x轴的距离与到y轴的距离之和是11,则a的值为( )
A. B.1 C. D.3
二、填空题
13.如图,在平面直角坐标系中,点A(0,4)在y轴正半轴上,点B(-3,0)在x轴负半轴上,且AB=5,点M坐标为(3,0),N点为线段OA上一动点,P为线段AB上的一动点,则MN+NP的最小值为 .
14.已知点的坐标为,且点在轴上,则的值为 .
15.平面直角坐标系xOy中,已知点P(m,m+2),点Q(n,0),点M(1,1),则PQ+QM最小值为 .
16.如图,一个机器人从O点出发,向正东方向走3米到达点,再向正北方向走6米到达点,再向正西方向走9米到达点,再向正南方向走12米到达点,再向正东方向走15米到达点,按如此规律走下去,当机器人走到点时,点的坐标是 .
17.在平面直角坐标系中,点所在的象限是 .
三、解答题
18.已知点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,求点P坐标.
19.如图是某学校的平面示意图,已知旗杆的位置是,实验室的位置是.
(1)画出图中的直角坐标系;
(2)写出图中食堂、图书馆的位置;
(3)已知办公楼的位置是,教学楼的位置是,在图中标出办公楼和教学楼的位置;
(4)如果一个单位长度表示30米,请求出宿舍楼到教学楼的实际距离.
20.如图,已知图中点和点的坐标分别为和.
(1)请在图中画出坐标轴建立适当的直角坐标系;
(2)写出点的坐标为________;
(3)连接、和得,在轴的负半轴有点满足,则点的坐标为________,________个平方单位;
21.嘉嘉从A处出发向北偏东走了30m,到达B处;淇淇从A处出发向南偏东走了40m,到达C处.
(1)用1cm表示10m,画图表示A,B,C的位置;
(2)A处在C处的______偏______度的方向上,距离C处______米;
(3)叙述A处相对于B处的位置.
22.哥哥从家里骑自行车出发,去超市途中遇到妹妹从超市走路回家,哥哥在超市买完东西后以原先速度骑车回家,在回去的路上又遇到了妹妹,便载妹妹一起回家,结果哥哥比按原先速度回家的时间晚了3分钟,二人离超市的距离和哥哥从家出发后的时间之间的关系如图所示(假设二人交流时间忽略不计).
(1)家与超市相距________;
(2)哥哥和妹妹第1次相遇时离超市的距离是多少?
(3)哥哥从家里出发到回家所用的时间是多少?
23.学校举行大型活动,用甲、乙两架无人机进行航拍,若无人机在上升过程中匀速飞行,甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,无人机所在高度(米)与时间(秒)之间的关系如图所示,根据图象回答下列问题:
(1)甲在空中停留时的高度是______米,甲出发______秒后乙开始起飞,点表示的意义是_________;
(2)甲、乙两架无人机的上升速度分别是多少米/秒?
(3)当时,两架无人机所在的高度相差多少米?
24.6月13日,某港口的潮水高度y()和时间x(h)的部分数据及函数图像如下:
x(h) … 11 12 13 14 15 16 17 18 …
y() … 189 137 103 80 101 133 202 260 …
(数据来自某海洋研究所)
(1)数学活动:
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图像.
②观察函数图像,当时,y的值为多少?当y的值最大时,x的值为多少?
(2)数学思考:
请结合函数图像,写出该函数的两条性质或结论.
(3)数学应用:
根据研究,当潮水高度超过260时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?
《14.3函数图像的画法》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C B D D B A D
题号 11 12
答案 D C
1.D
【分析】本题考查利用函数图象表示变量之间的关系,从图象可知,相同注水速度下,水面上升的速度随着注水时间的增加而减小,即可得出结论.
【详解】解:图象可知,相同注水速度下,水面上升的速度随着注水时间的增加而减小,
∴容器的形状可能是下窄上宽,
故选D.
2.C
【分析】根据函数的定义,对于x的每一个确定的值,y都有唯一的值与其对应,确定正确的选项.
【详解】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故B不符合题意;
C、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故C符合题意;
D、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故D不符合题意;
故选:C.
【点睛】本题考查了函数的定义,掌握函数的定义是解题关键.
3.C
【分析】根据度数表示纵坐标,圆圈数表示横坐标,可得答案.
【详解】解:因为记图中目标C的位置为,
所以点E的位置为.
故选:C
【点睛】此题主要考查了坐标确定位置,正确理解题意得出横纵坐标的意义是解题关键.
4.C
【分析】本题考查了坐标确定位置,根据题意可得到点的坐标,正确掌握点的坐标是解题的关键.
【详解】解:∵小敏家在学校正南方向,正东方向处,
∴横坐标为200,纵坐标为,
∴点的坐标为,
故选:C.
5.B
【分析】根据方向角的定义即可解答.
【详解】解:∵A在B西偏南的方向上,,
∴C在B的南偏东的方向上,
∵,,
∴km,
∴超市(记作C)在爱棣家的南偏东的方向上,相距.
故选:B.
【点睛】本题考查了方向角,根据题目的已知条件并结合图形分析是解题的关键.
6.D
【分析】本题考查了坐标位置的确定,根据位置的表示方法,第一个数表示距观察站的圈数,第二个数表示度数写出即可.
【详解】解:∵目标B用表示,目标D用表示,
∴第一个数表示距观察站的圈数,第二个数表示度数,
∴表示为的目标是:C.
故选:D.
7.D
【分析】根据确定位置的有序数对有两个数解答.
【详解】解:在平面直角坐标系中,要用两个数据才能表示一个点的位置,纵观各选项,只有东经,北纬能确定物体的位置,
故选:D
【点睛】本题考查了坐标确定位置,理解在平面直角坐标系中,要用两个数据才能表示一个点的位置是解题的关键.
8.B
【分析】根据“太阳神车”与“雪域金翅”的位置结果找到位置的表示方法,即可求解.
【详解】∵“太阳神车”的位置为(500,20°),“雪域金翅”的位置为(400,340°),
∴可知有序数对的第一个值为:目标距离观测点中心广场的距离,第二个值为:目标与观测点中心广场的连线与正东方向的旋转角度度数,
∴根据图形可知,“天地双雄”距离观测点中心广场的距离为:500,天地双雄”与观测点中心广场的连线与正东方向的旋转角度度数为120°,
即有序数对为(500,120°),
故选:B.
【点睛】本题考查了用有序数对表示位置的知识,理解题意是解答本题的关键.
9.A
【分析】本题考查了确定位置,解题的关键是根据坐标确定位置需要两个数据,对各选项分析判断后求解.
【详解】解:A、南偏西方向,无法确定物体的具体位置,故本选项符合题意;
B、某小区3座406室,位置明确,故本选项不符合题意;
C、东经,北纬,位置明确,故本选项不符合题意;
D、电影院3排4座,位置明确,故本选项不符合题意.
故选:A.
10.D
【分析】根据题意画出图形,根据直线a//x轴,得到直线a为直线y= 2,根据垂线段最短即可得出答案.
【详解】
如图,∵直线a// x轴,
∴直线a为直线y= 2,
当BC⊥a时,线段BC最短,
∴点C的坐标为(2, 2).
故选: D.
【点睛】本题考查了坐标与图形性质,掌握平行于x轴的坐标的特点,以及垂线段最短是解题的关键.
11.D
【分析】本题主要考查点所在象限,先根据第二象限内点的坐标符号特点确定m的正负,然后结合各选项即可解答.掌握第二象限的点的横坐标小于零、纵坐标大于零是解题的关键.
【详解】解:∵点在第二象限,
∴,
∴A、B、C选项不符合题意,D选项符合题意.
故选:D.
12.C
【分析】本题考查了坐标与图形的性质,熟练掌握第二象限的点的坐标特征是解题的关键.根据第二象限的点的坐标特征,得到,,再结合“点P到x轴的距离与到y轴的距离之和是11”,列出方程求出a的值即可解答.
【详解】解:点在第二象限,
,,
点P到x轴的距离为,到y轴的距离为,
由题意得,,
解得:.
故选:C.
13.
【分析】连接AM,根据点A(0,4),点B(-3,0),点M坐标为(3,0),得到OA=4,OB=3,OM=3,过M作MP⊥AB于P交OA于N,则此时,MN+NP的值最小,且MN+NP的最小值=MP,根据三角形的面积公式即可得到结论.
【详解】解:连接AM,
∵点A(0,4),点B(-3,0),点M坐标为(3,0),
∴OA=4,OB=3,OM=3,
过M作MP⊥AB于P交OA于N,
则此时,MN+NP的值最小,且MN+NP的最小值=MP,
∵, BM=6,OA=4,AB=5,
∴.
故答案为:.
【点睛】本题考查垂线段最短的应用,坐标与图形性质,三角形的面积公式,正确的作出图形是解题的关键.
14.
【分析】本题考查的是点的坐标,正确掌握相关性质内容是解题的关键.
根据轴上点的纵坐标等于0得出关于的方程,求出的值即可.
【详解】解:因为点的坐标为,且点在轴上,
,
解得,
故答案为:.
15.
【分析】根据点P(m,m+2)可知,点P在一次函数的图像上移动,作出图示,并作M关于x轴的对称点,过点作于点P,交x轴于点Q,连接,QM,利用“垂线段最短”原理,可知此时PQ+QM最小,最小值为的长度,利用等腰三角形的性质求解即可得出答案.
【详解】解:如图所示,由题意可知,点P(m,m+2)在一次函数的图像上移动, 一次函数分别交x轴、y轴于点A,B,作M关于x轴的对称点,过点作于点P,交x轴于点Q,连接,QM,利用“垂线段最短”原理,可知此时PQ+QM最小,最小值为的长.
点M(1,1),
由对称性质可知:点
一次函数的图像分别交x轴、y轴于点
令,解得,即点,令,解得,即点
为等腰三角形,
点P为AB的中点,则点
故答案为:
【点睛】本题考查了最值问题,涉及到一次函数的性质、等腰三角形的性质“三线合一”以及根据两点坐标求点之间的距离,思考问题时参照“将军饮马”模型,根据“垂线段最短”原理,将问题转化为求垂线段的长度是解决本题的关键.
16.
【分析】本题主要考查了坐标确定位置的运用,解题的关键是发现规律,利用规律解决问题,解题时注意:各象限内点的坐标特征为:第一象限:;第二象限:;第三象限:;第四象限:.
由于一个机器人从点出发,向正东方向走3米,到达点,那么点坐标为,再向正北走6米到达点,那么点坐标为,6),再向正西走9米到达点,那么点坐标为,然后依此类推,找出规律,即可求出的坐标.
【详解】解:根据题意可知:,
故点的坐标为;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
依此类推,可得点的坐标为,即.
故答案为:.
17.第二象限
【分析】本题考查判断点所在的象限,根据点的符号特征,进行判断即可.
【详解】解:∵,
∴,
∵,
∴点在第二象限,
故答案为:第二象限.
18.P点坐标为或
【分析】由题得,点P到两坐标轴的距离相等,则点P的横纵坐标绝对值相等,据此列式求解,即可得到a的值,进而确定点P的坐标;
【详解】解:∵点P的坐标为(2﹣a,3a+6),且点P到两坐标轴的距离相等,
∴|2-a|=|3a+6|,
化为:2-a=3a+6或2-a=-(3a+6),
解得a=-1或a=-4,
所以点P的坐标为(3,3)或(6,-6).
【点睛】本题主要考查了象限内点的坐标的特征,掌握象限内点的坐标的特征是解题的关键.
19.(1)见解析
(2)食堂、图书馆
(3)见解析
(4)
【分析】(1)根据旗杆的坐标可以得到原点的位置,建立平面直角坐标系即可;
(2)写出这两点的坐标即可;
(3)根据坐标,描出点的位置即可;
(4)宿舍楼到教学楼的距离是8个单位长度,乘以即可.
【详解】(1)解:直角坐标系如图所示;
(2)解:由图可知,食堂、图书馆;
(3)解:如图所示;
(4)解:由图可知宿舍楼到教学楼的实际距离为.
【点睛】本题考查了平面直角坐标系,点的坐标的表示方法,坐标确定位置,画出正确的平面直角坐标系是解题的关键.
20.(1)见解析
(2)
(3);
【分析】本题考查了直角坐标系、三角形的面积计算,能找到直角坐标系的原点、横纵坐标的正方向并画出直角坐标系是解答本题的关键.
(1)根据图中点和点的坐标确定原点的位置和横纵坐标的正方向即可得到答案;
(2)根据直角坐标的特点,即可写出的坐标;
(3)根据点在直角坐标系中的位置,先算出的面积,再根据三角形的面积公式即可算出答案.
【详解】(1)解:根据图中点和点的坐标确定原点的位置和横纵坐标的正方向,得到直角坐标系如下图:
(2)解:根据直角坐标系的特点,得到点的坐标为:,
故答案为:;
(3)解:画图如下:
根据点在直角坐标系中的位置,得到:,
假设点的坐标为,
,
又,
,
,
或,
在轴的负半轴,
,
故的坐标为,个平方单位,
故答案为:;.
21.(1)见解析
(2)北偏西,60,40
(3)A处在B处的南偏西30度,距离B处30米处
【分析】(1)确定比例尺为,图上1cm表示实际距离10m,明确方位角,画图;
(2)根据图形判断位置,A处在C处的北偏西度的方向上,距离C处40米;
(3)根据图形判断位置,A处在B处的南偏西30度,距离B处30米处;
【详解】(1)解:如图.
(2)解:A处在C处的北偏西度的方向上,距离C处40米;
(3)解:A处在B处的南偏西30度,距离B处30米处;
【点睛】本题考查比例尺,用方位角表示位置;理解方位角的表示方法是解题的关键.
22.(1)8
(2)4千米
(3)103分钟
【分析】本题考查了从函数图象中获取信息,采用数形结合的思想是解此题的关键.
(1)根据图象即可得出答案;
(2)先求出哥哥骑车的速度,根据图象,相遇时间为20分钟,计算即可得出哥哥和妹妹第1次相遇时离超市的距离;
(3)根据题意列式计算即可得出答案.
【详解】(1)解:由图可得:家与超市相距;
(2)解:由图可得:哥哥骑车的速度为:(千米/分钟),
根据图象,相遇时间为20分钟,
∴(千米),
∴哥哥和妹妹第1次相遇时离超市的距离是4千米;
(3)解:由题意得:(分钟).
∴哥哥从家里出发到回家所用的时间是103分钟.
23.(1),,秒时甲、乙无人机所在高度都是米
(2)甲、乙两架无人机的上升速度分别为4米/秒、6米/秒
(3)当时,两架无人机所在的高度相差米
【分析】(1)根据题意得,至时甲在空中停留,停留时的高度是米,根据甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞得甲出发秒后乙开始起飞,根据所给图象即可得点表示的意义;
(2)根据“速度=路程÷时间”进行计算即可得;
(3)根据速度、时间与路程的关系式列式进行计算即可得.
【详解】(1)解:根据题意得,至时甲在空中停留,停留时的高度是米,
∵甲先从地面起飞,在空中停留一会儿后继续上升,此时乙从地面起飞,
∴甲出发秒后乙开始起飞,
点表示的意义是:秒时甲、乙无人机所在高度都是米,
故答案为:,,秒时甲、乙无人机所在高度都是米;
(2)解:甲架无人机的上升速度:,
乙架无人机的上升速度:,
答:甲、乙两架无人机的上升速度分别为4米/秒、6米/秒.
(3)解:,
答:当时,两架无人机所在的高度相差米.
【点睛】本题考查了图象问题,解题的关键是理解题意,根据所给图象获取信息,正确计算.
24.(1)①见解析;②,
(2)①当时,y随x的增大而增大;②当时,y有最小值80
(3)和
【分析】(1)①根据表格数据在函数图像上描点连线即可;
②根据函数图像估计即可;
(2)从增减性、最值等方面说明即可;
(3)根据图像找到y=260时所有的x值,再结合图像判断即可.
【详解】(1)①
②观察函数图像:
当时,;
当y的值最大时,;.
(2)答案不唯一.
①当时,y随x的增大而增大;
②当时,y有最小值80.
(3)根据图像可得:当潮水高度超过260时和,
【点睛】本题考查函数图像的画法、从函数图像获取信息,准确的画出函数图像是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
