14.4一次函数同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
14.4一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列问题中,变量y与x成一次函数关系的是( )
A.长铁丝折成长为,宽为的长方形
B.斜边长为的直角三角形的直角边和
C.圆的面积与它的半径
D.路程一定时,时间和速度的关系
2.下列各点不在函数图象上的是( )
A. B. C. D.
3.若关于的函数是正比例函数,则应满足的条件是( )
A. B. C. D.
4.根据如图所示的程序计算函数的值,若输入的值是6,则输出的值是1,若输入的值是2,则输出的值是( )
A.4 B.10 C.19 D.21
5.已知函数是y关于x的一次函数,则m的取值范围是( )
A. B. C. D.m为任意实数
6.下列问题中,两个变量之间是正比例函数关系的是( )
A.矩形的周长一定,它的长y与宽x
B.书的总页数一定,未读的页数与已读的页数
C.某场电影票价固定,该场电影售票收入为y元与售票数量为x张
D.圆的面积y(cm2)与它的半径x(cm)之间的关系
7.下列函数中,是正比例函数的是( )
A. B. C. D.
8.在平面直角坐标系中,已知点在直线上,则的值为( )
A.1 B. C.2 D.
9.已知一次函数,是常数,且,若,则该一次函数的图象必经过点( )
A. B. C. D.
10.已知点在的图象上,则的值为( )
A. B. C. D.
11.经过点P(1,-2)的一次函数是( )
A.y=-x-1 B.y=x-1
C.y=-x+1 D.y=x+1
12.函数的图象一定经过点( )
A. B. C. D.
二、填空题
13.若函数是关于的一次函数,则满足 ;
若该函数是关于的正比例函数,则,满足 ;
若,,则函数关系式是 .
14.函数是一次函数,则常数k的值为 .
15.已知函数,当k 时,它为一次函数;当k 时,它是正比例函数.
16.已知点在一次函数的图像上,则的值是 .
17.设一次函数.若当时,;当时,,则的取值范围是
三、解答题
18.如图,△ABC的两顶点分别为B(0,0),C(4,0),顶点A在直线l:y=﹣x+3上.
(1)当△ABC是以BC为底的等腰三角形时,求点A的坐标;
(2)当△ABC的面积为4时,求点A的坐标;
(3)在直线l上是否存在点A,使∠BAC=90°?若存在,求出点A的坐标;若不存在请说明理由.
19.下列式子,哪些y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)
(2)
(3)
20.已知.
(1)当m,n取何值时,y是x的一次函数?
(2)当m,n取何值时,y是x的正比例函数?
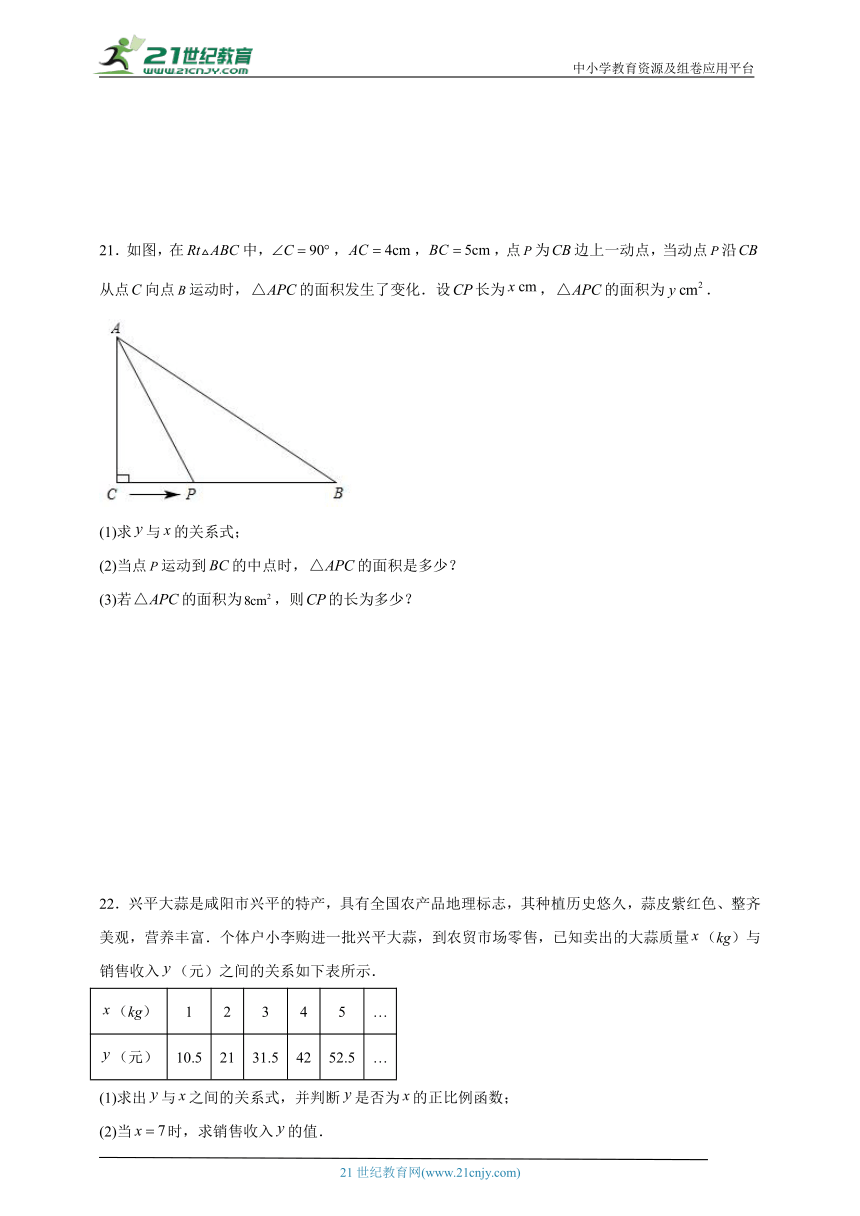
21.如图,在中,,,,点为边上一动点,当动点沿从点向点运动时,的面积发生了变化.设长为,的面积为.
(1)求与的关系式;
(2)当点运动到的中点时,的面积是多少?
(3)若的面积为,则的长为多少?
22.兴平大蒜是咸阳市兴平的特产,具有全国农产品地理标志,其种植历史悠久,蒜皮紫红色、整齐美观,营养丰富.个体户小李购进一批兴平大蒜,到农贸市场零售,已知卖出的大蒜质量(kg)与销售收入(元)之间的关系如下表所示.
(kg) 1 2 3 4 5 …
(元) 10.5 21 31.5 42 52.5 …
(1)求出与之间的关系式,并判断是否为的正比例函数;
(2)当时,求销售收入的值.
23.学校阅览室有一种能坐4人的方桌,如果多于4人,就把方桌按图中的方式摆放,2张方桌摆放到一起能坐6人,请你结合这个规律,回答问题:
(1)写出总人数y(人)与方桌数x(张)之间的函数解析式(不要求写自变量的取值范围),并判断y是不是x的一次函数;
(2)若八年级(1)班有42人去阅览室看书,则需要多少张这样的方桌?
24.已知函数,
(1)当m、n为何值时,此函数是一次函数?
(2)当m、n为何值时,此函数是正比例函数?
《14.4一次函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A B C A C A A
题号 11 12
答案 A B
1.A
【分析】分别求出各个选项的函数关系式,即可得到答案.
【详解】解:A、∵长铁丝折成长为,宽为的长方形,∴,满足一次函数关系,符合题意;
B、∵斜边长为的直角三角形的直角边和,∴,不满足一次函数的关系,不符合题意;
C、圆的面积与它的半径,关系式为,不是一次函数关系,不符合题意;
D、路程一定时,时间和速度的关系式为(k表示路程),不是一次函数关系,不符合题意;
故选A
【点睛】本题主要考查了一次函数的定义,熟知如果x、y满足(,k、b是常数),那么y是x的一次函数是解题的关键.
2.C
【分析】根据题意,分别令代入函数解析式,即可求解.
【详解】解:A.当时,,则在图象上,故该选项正确,不符合题意;
B. 当时,,则在图象上,故该选项正确,不符合题意;
C. 当时,,则不在图象上,故该选项不正确,符合题意;
D. 当时,,则在图象上,故该选项正确,不符合题意;
故选:C.
【点睛】本题考查了一次函数的性质,熟练掌握一次函数的性质是解题的关键.
3.C
【分析】本题考查了正比例函数的定义,一般地,把形如的函数叫作正比例函数,熟练掌握正比例函数的定义是解此题的关键.
【详解】解:∵关于的函数是正比例函数,
∴,
故选:C.
4.A
【分析】根据程序框图,将代入求出的值,将代入即可求出的值.
【详解】当时,,解得:,
当时,.
故选:A.
【点睛】本题考查了函数解析式的函数值求法,熟练掌握函数解析式的代入求值是解题的关键.
5.B
【分析】根据一次函数的定义:,进行求解即可.
【详解】解:是y关于x的一次函数,
∴,即;
故选B.
【点睛】本题考查一次函数的定义.熟练掌握,是解题的关键.
6.C
【分析】本题考查正比例函数的定义,根据正比例函数的定义逐一进行判断即可.
【详解】解:A、矩形的周长一定,它的长y与宽x是一次函数的关系,不是正比例函数的关系;不符合题意;
B、书的总页数一定,未读的页数与已读的页数是一次函数的关系,不是正比例函数的关系;不符合题意;
C、某场电影票价固定,该场电影售票收入为y元与售票数量为x张是正比例函数,符合题意;
D、圆的面积y(cm2)与它的半径x(cm)之间的关系不是正比例函数,不符合题意;
故选C.
7.A
【分析】根据正比例函数的定义进行判断即可.
【详解】A、y是x的正比例函数,所以A选项符合题意;
B、y是x的二次函数,所以B选项不符合题意;
C、y是x的反比例函数,所以C选项不符合题意;
D、y是x的一次函数,所以D选项不符合题意;
故选:A.
【点睛】本题考查了正比例函数的定义:一般地,形如y = kx(k是常数,k ≠ 0)的函数叫做正比例函数,熟练掌握知识点是解题的关键.
8.C
【分析】将代入,变形即可得答案.
【详解】解:∵点在直线上,
∴,
∴,
故选∶C.
【点睛】本题考查一次函数图象上点坐标的特征,解题的关键是掌握一个点在函数图象上,则这个点的坐标满足该函数的解析式.
9.A
【分析】本题考查了一次函数图象上点的坐标特征,牢记“直线上任意一点的坐标都满足函数关系式”是解题的关键.由,可得出,再利用一次函数图象上点的坐标特征,即可得出该一次函数的图象必经过点.
【详解】解:,即,
一次函数,是常数,且的图象必经过点.
故选:A
10.A
【分析】本题考查了一次函数图象上点的坐标特征,利用一次函数图象上点的坐标特征,可得出,变形后即可得出结论.
【详解】解:点在的图象上,
,
.
故选:A.
11.A
【分析】把点P的坐标分别代入四个选项的解析式即可判断.
【详解】解:A.当x=1时,y=-x-1=-2,故一次函数y=-x-1过点P(1,-2);
B.当x=1时,y=x-1=0,故一次函数y=x-1不过点P(1,-2);
C.当x=1时,y=-x+1=0,故一次函数y=-x+1不过点P(1,-2);
D.当x=1时,y=x+1=2,故一次函数y=x+1不过点P(1,-2);
故选:A.
【点睛】本题考查了一次函数图象上点的坐标特征,熟练掌握图象上点的坐标满足函数关系是解此题的关键.
12.B
【分析】本题考查了一次函数图象上点的坐标特征的应用,解此题的关键是把点的坐标代入函数解析式看看两边是否相等.把点的坐标代入进行判断即可.
【详解】解:A、把代入函数得,即点不在正比例函数的图象上,故本选项不符合;
B、把代入函数得,即点在正比例函数的图象上,故本选项符合;
C、把代入函数得,即点不在正比例函数的图象上,故本选项不符合;
D、把代入函数得,即点不在正比例函数的图象上,故本选项不符合.
故选:B.
13. 且
【分析】本题主要考查了一次函数和正比例函数的知识,熟练掌握相关定义是解题关键.根据一次函数和正比例函数的定义,注意分析计算即可.
【详解】解:若函数是关于的一次函数,
则有,解得;
若该函数是关于的正比例函数,
则有,且,
解得且;
若,,则函数关系式是.
故答案为:;且;.
14.
【分析】根据一次函数的定义,形如的函数为一次函数,求解即可.
【详解】解:由题意可得:,解得
故答案为:
【点睛】此题考查了一次函数的定义,解题的关键是掌握一次函数的定义.
15.
【分析】本题主要考查了一次函数和正比例函数的解析式,根据一次函数的解析式是,正比例函数的解析式是得出答案.
【详解】解:当是一次函数时,
得,
∴,
当是正比例函数时,
得且,
解得,
故答案为:,.
16.6
【分析】直接把点代入一次函数,求出的值,代入代数式进行计算即可.
【详解】解:点在一次函数的图象上,
,
,
.
故答案为:6.
【点睛】本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解题的关键.
17.
【分析】根据题意确定有关b的不等式组,从而确定b的取值范围.
【详解】解:∵一次函数y= 3x+b,若当x= 2时,y>0;当x=2时,y<0,
∴,
解得: 6<b<6,
故答案为: 6<b<6.
【点睛】考查了一次函数图象与系数的关系,解题的关键是根据题意列出有关b的不等式组,难度不大.
18.(1)A(2,2);
(2)(2,2)或(10,﹣2);
(3)在直线l上存在点A,使∠BAC=90°,此时点A的坐标是(2,2)或(3.6,1.2)
【分析】(1)以BC为底的等腰三角形,点A是BC的中垂线与直线l的交点,据此求解即可;
(2)根据△ABC的面积求得点A的纵坐标,把点A的纵坐标代入直线方程即可求得其横坐标;
(3)设点A的坐标为,根据两点间距离公式表示出,,,再利用勾股定理建立方程,求解即可.
【详解】(1)如图,当△ABC是以BC为底的等腰三角形时,点A在BC的中垂线上.
∵B(0,0),C(4,0),
∴BC的中垂线为x=2.
又点A在直线l:y=﹣x+3上,
∴y=﹣×2+3=2,
即A(2,2);
(2)设A(a,b).则依题意得
BC |b|=4,即×4|b|=4,
解得|b|=2
∴b=±2.
①当b=2时,2=﹣a+3,
解得 a=2
则A(2,2);
②当b=﹣2时,﹣2=﹣a+3,
解得 a=10
则A(10,﹣2).
综上所述,点A的坐标是(2,2)或(10,﹣2);
(3)设点A的坐标为,
B(0,0),C(4,0),
,,,
∠BAC=90°,
,即,
解得或,
所以,在直线l上存在点A,使∠BAC=90°,此时点A的坐标是(2,2)或(3.6,1.2).
【点睛】本题综合考查了等腰三角形的性质,一次函数图象上点的坐标特征,三角形的面积公式以及勾股定理等知识点.解(2)题的过程中,一定要对点A的纵坐标进行分类讨论,以防漏解.
19.(1)不是正比例函数
(2)不是正比例函数
(3)是正比例函数,正比例系数是2
【分析】本题考查了正比例函数的定义,熟练掌握正比例函数的定义是解题的关键.根据正比例函数的一般形式为判断即可.
(1)根据正比例函数的一般形式为判断即可.
(2)根据正比例函数的一般形式为判断即可.
(3)先去括号化简,根据正比例函数的一般形式为判断即可.
【详解】(1)解:不是正比例函数.
(2)解:不是正比例函数.
(3)解:,是正比例函数,正比例系数是2.
20.(1),n为任意实数
(2),
【分析】本题考查了一次函数和正比例函数的定义,形如的是一次函数,形如的是正比例函数.
(1)根据一次函数的定义即可解答;
(2)根据正比例函数的定义即可解答.
【详解】(1)解:∵是一次函数,
∴,
解得:,
∴,n为任意实数;
(2)解:∵是正比例函数,
∴,
解得:.
21.(1)
(2)点运动到的中点时,的面积为
(3)当的面积为时,的长为
【分析】对于(1),根据三角形的面积公式用含有x的代数式表示y即可;
对于(2),将代入关系式计算即可;
对于(3),将代入关系式求出x即可.
【详解】(1),所以与的关系式为;
(2)当时,,
所以点运动到的中点时,的面积为;
(3)当时,,解得,
所以当的面积为时,的长为.
【点睛】本题主要考查了求函数关系式,求自变量,求函数值等,准确的计算是解题的关键.
22.(1);是的正比例函数;
(2).
【分析】此题考查了列函数解析式和正比例函数、求函数值等知识.
(1)由表格可知: 大蒜质量量每增加,销售收入增加10.5元,据此得到函数解析式,再根据正比例函数的定义进行判断即可;
(2)把代入(1)中的函数解析式即可.
【详解】(1)解:由表格可知: 大蒜质量量每增加,销售收入增加10.5元,
∴,
即;
则是的正比例函数;
(2)当时,,
即当时,销售收入的值为.
23.(1)
(2)20张
【分析】(1)根据第一张桌子可坐4人,以后每多一张桌子多2人,可列函数关系式,再判断即可;
(2)将y=42代入(1)中的函数关系式即可求出.
【详解】(1)解:∵一张方桌坐4人,每多一张方桌就多坐2人,
∴如果是x张方桌,则所坐人数是.
∴y与x之间的函数解析式为,
(2)解:把代入,
得,解得.
答:需要20张这们样的方桌.
【点睛】本题考查了根据图形求一次函数的解析式,及一次函数的判断、求自变量的取值,根据图形列出函数表达式是解题的关键.
24.(1)
(2)n=1,m=-1
【分析】(1)根据一次函数的定义知,且,据此可以求得、的值;
(2)根据正比例函数的定义知,,据此可以求得、的值.
【详解】(1)解:当函数是一次函数时,
,且,
解得,,;
(2)解:当函数是正比例函数时,
,
解得,,.
【点睛】本题考查了一次函数、正比例函数的定义,解题的关键是掌握正比例函数是一次函数的一种特殊形式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
14.4一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列问题中,变量y与x成一次函数关系的是( )
A.长铁丝折成长为,宽为的长方形
B.斜边长为的直角三角形的直角边和
C.圆的面积与它的半径
D.路程一定时,时间和速度的关系
2.下列各点不在函数图象上的是( )
A. B. C. D.
3.若关于的函数是正比例函数,则应满足的条件是( )
A. B. C. D.
4.根据如图所示的程序计算函数的值,若输入的值是6,则输出的值是1,若输入的值是2,则输出的值是( )
A.4 B.10 C.19 D.21
5.已知函数是y关于x的一次函数,则m的取值范围是( )
A. B. C. D.m为任意实数
6.下列问题中,两个变量之间是正比例函数关系的是( )
A.矩形的周长一定,它的长y与宽x
B.书的总页数一定,未读的页数与已读的页数
C.某场电影票价固定,该场电影售票收入为y元与售票数量为x张
D.圆的面积y(cm2)与它的半径x(cm)之间的关系
7.下列函数中,是正比例函数的是( )
A. B. C. D.
8.在平面直角坐标系中,已知点在直线上,则的值为( )
A.1 B. C.2 D.
9.已知一次函数,是常数,且,若,则该一次函数的图象必经过点( )
A. B. C. D.
10.已知点在的图象上,则的值为( )
A. B. C. D.
11.经过点P(1,-2)的一次函数是( )
A.y=-x-1 B.y=x-1
C.y=-x+1 D.y=x+1
12.函数的图象一定经过点( )
A. B. C. D.
二、填空题
13.若函数是关于的一次函数,则满足 ;
若该函数是关于的正比例函数,则,满足 ;
若,,则函数关系式是 .
14.函数是一次函数,则常数k的值为 .
15.已知函数,当k 时,它为一次函数;当k 时,它是正比例函数.
16.已知点在一次函数的图像上,则的值是 .
17.设一次函数.若当时,;当时,,则的取值范围是
三、解答题
18.如图,△ABC的两顶点分别为B(0,0),C(4,0),顶点A在直线l:y=﹣x+3上.
(1)当△ABC是以BC为底的等腰三角形时,求点A的坐标;
(2)当△ABC的面积为4时,求点A的坐标;
(3)在直线l上是否存在点A,使∠BAC=90°?若存在,求出点A的坐标;若不存在请说明理由.
19.下列式子,哪些y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)
(2)
(3)
20.已知.
(1)当m,n取何值时,y是x的一次函数?
(2)当m,n取何值时,y是x的正比例函数?
21.如图,在中,,,,点为边上一动点,当动点沿从点向点运动时,的面积发生了变化.设长为,的面积为.
(1)求与的关系式;
(2)当点运动到的中点时,的面积是多少?
(3)若的面积为,则的长为多少?
22.兴平大蒜是咸阳市兴平的特产,具有全国农产品地理标志,其种植历史悠久,蒜皮紫红色、整齐美观,营养丰富.个体户小李购进一批兴平大蒜,到农贸市场零售,已知卖出的大蒜质量(kg)与销售收入(元)之间的关系如下表所示.
(kg) 1 2 3 4 5 …
(元) 10.5 21 31.5 42 52.5 …
(1)求出与之间的关系式,并判断是否为的正比例函数;
(2)当时,求销售收入的值.
23.学校阅览室有一种能坐4人的方桌,如果多于4人,就把方桌按图中的方式摆放,2张方桌摆放到一起能坐6人,请你结合这个规律,回答问题:
(1)写出总人数y(人)与方桌数x(张)之间的函数解析式(不要求写自变量的取值范围),并判断y是不是x的一次函数;
(2)若八年级(1)班有42人去阅览室看书,则需要多少张这样的方桌?
24.已知函数,
(1)当m、n为何值时,此函数是一次函数?
(2)当m、n为何值时,此函数是正比例函数?
《14.4一次函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A B C A C A A
题号 11 12
答案 A B
1.A
【分析】分别求出各个选项的函数关系式,即可得到答案.
【详解】解:A、∵长铁丝折成长为,宽为的长方形,∴,满足一次函数关系,符合题意;
B、∵斜边长为的直角三角形的直角边和,∴,不满足一次函数的关系,不符合题意;
C、圆的面积与它的半径,关系式为,不是一次函数关系,不符合题意;
D、路程一定时,时间和速度的关系式为(k表示路程),不是一次函数关系,不符合题意;
故选A
【点睛】本题主要考查了一次函数的定义,熟知如果x、y满足(,k、b是常数),那么y是x的一次函数是解题的关键.
2.C
【分析】根据题意,分别令代入函数解析式,即可求解.
【详解】解:A.当时,,则在图象上,故该选项正确,不符合题意;
B. 当时,,则在图象上,故该选项正确,不符合题意;
C. 当时,,则不在图象上,故该选项不正确,符合题意;
D. 当时,,则在图象上,故该选项正确,不符合题意;
故选:C.
【点睛】本题考查了一次函数的性质,熟练掌握一次函数的性质是解题的关键.
3.C
【分析】本题考查了正比例函数的定义,一般地,把形如的函数叫作正比例函数,熟练掌握正比例函数的定义是解此题的关键.
【详解】解:∵关于的函数是正比例函数,
∴,
故选:C.
4.A
【分析】根据程序框图,将代入求出的值,将代入即可求出的值.
【详解】当时,,解得:,
当时,.
故选:A.
【点睛】本题考查了函数解析式的函数值求法,熟练掌握函数解析式的代入求值是解题的关键.
5.B
【分析】根据一次函数的定义:,进行求解即可.
【详解】解:是y关于x的一次函数,
∴,即;
故选B.
【点睛】本题考查一次函数的定义.熟练掌握,是解题的关键.
6.C
【分析】本题考查正比例函数的定义,根据正比例函数的定义逐一进行判断即可.
【详解】解:A、矩形的周长一定,它的长y与宽x是一次函数的关系,不是正比例函数的关系;不符合题意;
B、书的总页数一定,未读的页数与已读的页数是一次函数的关系,不是正比例函数的关系;不符合题意;
C、某场电影票价固定,该场电影售票收入为y元与售票数量为x张是正比例函数,符合题意;
D、圆的面积y(cm2)与它的半径x(cm)之间的关系不是正比例函数,不符合题意;
故选C.
7.A
【分析】根据正比例函数的定义进行判断即可.
【详解】A、y是x的正比例函数,所以A选项符合题意;
B、y是x的二次函数,所以B选项不符合题意;
C、y是x的反比例函数,所以C选项不符合题意;
D、y是x的一次函数,所以D选项不符合题意;
故选:A.
【点睛】本题考查了正比例函数的定义:一般地,形如y = kx(k是常数,k ≠ 0)的函数叫做正比例函数,熟练掌握知识点是解题的关键.
8.C
【分析】将代入,变形即可得答案.
【详解】解:∵点在直线上,
∴,
∴,
故选∶C.
【点睛】本题考查一次函数图象上点坐标的特征,解题的关键是掌握一个点在函数图象上,则这个点的坐标满足该函数的解析式.
9.A
【分析】本题考查了一次函数图象上点的坐标特征,牢记“直线上任意一点的坐标都满足函数关系式”是解题的关键.由,可得出,再利用一次函数图象上点的坐标特征,即可得出该一次函数的图象必经过点.
【详解】解:,即,
一次函数,是常数,且的图象必经过点.
故选:A
10.A
【分析】本题考查了一次函数图象上点的坐标特征,利用一次函数图象上点的坐标特征,可得出,变形后即可得出结论.
【详解】解:点在的图象上,
,
.
故选:A.
11.A
【分析】把点P的坐标分别代入四个选项的解析式即可判断.
【详解】解:A.当x=1时,y=-x-1=-2,故一次函数y=-x-1过点P(1,-2);
B.当x=1时,y=x-1=0,故一次函数y=x-1不过点P(1,-2);
C.当x=1时,y=-x+1=0,故一次函数y=-x+1不过点P(1,-2);
D.当x=1时,y=x+1=2,故一次函数y=x+1不过点P(1,-2);
故选:A.
【点睛】本题考查了一次函数图象上点的坐标特征,熟练掌握图象上点的坐标满足函数关系是解此题的关键.
12.B
【分析】本题考查了一次函数图象上点的坐标特征的应用,解此题的关键是把点的坐标代入函数解析式看看两边是否相等.把点的坐标代入进行判断即可.
【详解】解:A、把代入函数得,即点不在正比例函数的图象上,故本选项不符合;
B、把代入函数得,即点在正比例函数的图象上,故本选项符合;
C、把代入函数得,即点不在正比例函数的图象上,故本选项不符合;
D、把代入函数得,即点不在正比例函数的图象上,故本选项不符合.
故选:B.
13. 且
【分析】本题主要考查了一次函数和正比例函数的知识,熟练掌握相关定义是解题关键.根据一次函数和正比例函数的定义,注意分析计算即可.
【详解】解:若函数是关于的一次函数,
则有,解得;
若该函数是关于的正比例函数,
则有,且,
解得且;
若,,则函数关系式是.
故答案为:;且;.
14.
【分析】根据一次函数的定义,形如的函数为一次函数,求解即可.
【详解】解:由题意可得:,解得
故答案为:
【点睛】此题考查了一次函数的定义,解题的关键是掌握一次函数的定义.
15.
【分析】本题主要考查了一次函数和正比例函数的解析式,根据一次函数的解析式是,正比例函数的解析式是得出答案.
【详解】解:当是一次函数时,
得,
∴,
当是正比例函数时,
得且,
解得,
故答案为:,.
16.6
【分析】直接把点代入一次函数,求出的值,代入代数式进行计算即可.
【详解】解:点在一次函数的图象上,
,
,
.
故答案为:6.
【点睛】本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解题的关键.
17.
【分析】根据题意确定有关b的不等式组,从而确定b的取值范围.
【详解】解:∵一次函数y= 3x+b,若当x= 2时,y>0;当x=2时,y<0,
∴,
解得: 6<b<6,
故答案为: 6<b<6.
【点睛】考查了一次函数图象与系数的关系,解题的关键是根据题意列出有关b的不等式组,难度不大.
18.(1)A(2,2);
(2)(2,2)或(10,﹣2);
(3)在直线l上存在点A,使∠BAC=90°,此时点A的坐标是(2,2)或(3.6,1.2)
【分析】(1)以BC为底的等腰三角形,点A是BC的中垂线与直线l的交点,据此求解即可;
(2)根据△ABC的面积求得点A的纵坐标,把点A的纵坐标代入直线方程即可求得其横坐标;
(3)设点A的坐标为,根据两点间距离公式表示出,,,再利用勾股定理建立方程,求解即可.
【详解】(1)如图,当△ABC是以BC为底的等腰三角形时,点A在BC的中垂线上.
∵B(0,0),C(4,0),
∴BC的中垂线为x=2.
又点A在直线l:y=﹣x+3上,
∴y=﹣×2+3=2,
即A(2,2);
(2)设A(a,b).则依题意得
BC |b|=4,即×4|b|=4,
解得|b|=2
∴b=±2.
①当b=2时,2=﹣a+3,
解得 a=2
则A(2,2);
②当b=﹣2时,﹣2=﹣a+3,
解得 a=10
则A(10,﹣2).
综上所述,点A的坐标是(2,2)或(10,﹣2);
(3)设点A的坐标为,
B(0,0),C(4,0),
,,,
∠BAC=90°,
,即,
解得或,
所以,在直线l上存在点A,使∠BAC=90°,此时点A的坐标是(2,2)或(3.6,1.2).
【点睛】本题综合考查了等腰三角形的性质,一次函数图象上点的坐标特征,三角形的面积公式以及勾股定理等知识点.解(2)题的过程中,一定要对点A的纵坐标进行分类讨论,以防漏解.
19.(1)不是正比例函数
(2)不是正比例函数
(3)是正比例函数,正比例系数是2
【分析】本题考查了正比例函数的定义,熟练掌握正比例函数的定义是解题的关键.根据正比例函数的一般形式为判断即可.
(1)根据正比例函数的一般形式为判断即可.
(2)根据正比例函数的一般形式为判断即可.
(3)先去括号化简,根据正比例函数的一般形式为判断即可.
【详解】(1)解:不是正比例函数.
(2)解:不是正比例函数.
(3)解:,是正比例函数,正比例系数是2.
20.(1),n为任意实数
(2),
【分析】本题考查了一次函数和正比例函数的定义,形如的是一次函数,形如的是正比例函数.
(1)根据一次函数的定义即可解答;
(2)根据正比例函数的定义即可解答.
【详解】(1)解:∵是一次函数,
∴,
解得:,
∴,n为任意实数;
(2)解:∵是正比例函数,
∴,
解得:.
21.(1)
(2)点运动到的中点时,的面积为
(3)当的面积为时,的长为
【分析】对于(1),根据三角形的面积公式用含有x的代数式表示y即可;
对于(2),将代入关系式计算即可;
对于(3),将代入关系式求出x即可.
【详解】(1),所以与的关系式为;
(2)当时,,
所以点运动到的中点时,的面积为;
(3)当时,,解得,
所以当的面积为时,的长为.
【点睛】本题主要考查了求函数关系式,求自变量,求函数值等,准确的计算是解题的关键.
22.(1);是的正比例函数;
(2).
【分析】此题考查了列函数解析式和正比例函数、求函数值等知识.
(1)由表格可知: 大蒜质量量每增加,销售收入增加10.5元,据此得到函数解析式,再根据正比例函数的定义进行判断即可;
(2)把代入(1)中的函数解析式即可.
【详解】(1)解:由表格可知: 大蒜质量量每增加,销售收入增加10.5元,
∴,
即;
则是的正比例函数;
(2)当时,,
即当时,销售收入的值为.
23.(1)
(2)20张
【分析】(1)根据第一张桌子可坐4人,以后每多一张桌子多2人,可列函数关系式,再判断即可;
(2)将y=42代入(1)中的函数关系式即可求出.
【详解】(1)解:∵一张方桌坐4人,每多一张方桌就多坐2人,
∴如果是x张方桌,则所坐人数是.
∴y与x之间的函数解析式为,
(2)解:把代入,
得,解得.
答:需要20张这们样的方桌.
【点睛】本题考查了根据图形求一次函数的解析式,及一次函数的判断、求自变量的取值,根据图形列出函数表达式是解题的关键.
24.(1)
(2)n=1,m=-1
【分析】(1)根据一次函数的定义知,且,据此可以求得、的值;
(2)根据正比例函数的定义知,,据此可以求得、的值.
【详解】(1)解:当函数是一次函数时,
,且,
解得,,;
(2)解:当函数是正比例函数时,
,
解得,,.
【点睛】本题考查了一次函数、正比例函数的定义,解题的关键是掌握正比例函数是一次函数的一种特殊形式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
