积的乘方
图片预览







文档简介
课件21张PPT。15.2.3 积的乘方涪陵十八中 初二数学备课组 1、叙述同底数幂乘法法则并用字母表示。2、叙述幂的乘方法则 并用字母表示。 语言叙述:同底数幂相乘,底数不变,指数相加。
字母表示:am·an=am+n ( m、n都为正整数)语言叙述:幂的乘方,底数不变,指数相乘。
字母表示:(am)n=amn (m,n都是正整数)
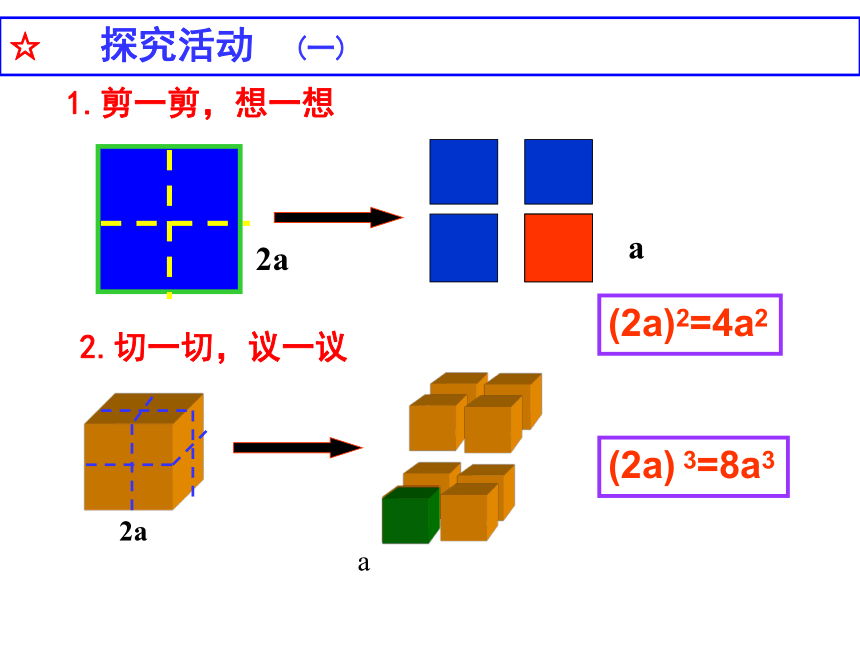
☆ 课前热身 1.2.1.剪一剪,想一想a2aa2.切一切,议一议☆ 探究活动 (一)(2a)2=4a2(2a) 3=8a3 2、比较下列各组算式的计算结果:
[2 ×(-3)]2 与 22 ×(-3)2 ;
[(-2)×(-5)]3与(-2)3 ×(-5)3
1、计算: (2×3)2与22 × 32,我们发现了什么? ∵ (2×3)2=62=36 ; 22 ×32=4×9=36
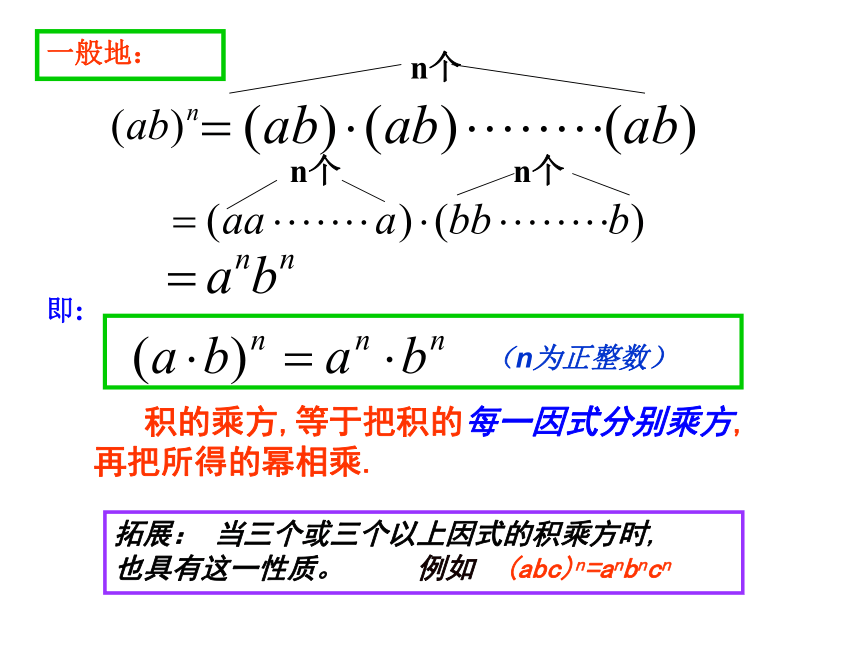
∴ (2×3)2 =22 × 32 都 相 等 ☆ 探究活动 (二) (1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.这两道题有什么特点?观察底数。底数为两个因式相乘,积的形式。我们学过的幂的运算性质适用吗?这种形式为积的乘方 ☆ 探究活动 (三) 同理:根据上述方法计算下列各题:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)积的乘方有什么规律呢?分组讨论积的乘方的运算性质:思考:积的乘方(ab)n =?一般地:n个n个n个即: 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(n为正整数)拓展: 当三个或三个以上因式的积乘方时, 也具有这一性质。 例如 (abc)n=anbncn例1:计算:
(1) (-3x)3 (2) (-5ab)2
(3) (xy2)2 (4) (-2xy3z2)4 解:(1)原式= (2)原式= (3)原式= (4)原式== -27x3=25a2b2 =x2y4=16x4y12z8(-3)3x3(-5)2a2b2x2(y2)2(-2)4x4(y3)4(z2)4能不能用积的乘方的性质计算?分析:以上各题底数都含有两个或两个以上的因式,我们运用积的乘方的运算性质。注意:
(1)负数乘方的符号法则。
(2)积的乘方等于积中“每一个”因式
乘方的积,防止有的因式漏乘方错误。
(3)在计算(-2xy3z2)4=(-2)4x4(y3)4(z2)4
=16x4y12z8的过程中,应把y3 , z2 看作一个数,再利用积的乘方性质进行计算。 思考: (-a)n= -an(n为正整数)对吗?当n为奇数时, (-a)n= -an(n为正整数)
当n为偶数时, (-a)n=an(n为正整数)
(体现了分类的思想)(1)(ab2)3=ab6 ( ) ×××(2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( )(4) -(-ab2)2=a2b4 ( )1、判断: √练一练2、计算:
(1) (ab)8 (2) (2m)3
(3) (-xy)5 (4) (5ab2)3
(5) (2×102)2 (6) (-3×103)3(2)8m3(3) –x5y5(4)125a3b6(5) 4×104(6) -27 ×109答案: (1)a8b8 3、计算:
(1)(-2x2y3)3 答案(2) 81a12b8c4答案 (1) -8x6y9(2) (-3a3b2c)41 计算: a3 ·a4· a+(a2)4+(-2a4)2解:原式=a3+4+1+a2×4+(-2)2 · (a4)2=a8+a8+4a8=6a8试一试:2 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除,最后算加减。=2x9-27x9+25x9=0一起探讨:(0.04)2009×[(-5)2009]2=?=(0.22)2009 × 54018=(0.2)4018 × 54008=(0.2 ×5)4018=14018解法一: (0.04)2009×[(-5)2009]2=1=(0.04)2009 × [(-5)2]2009=(0.04×25)2009=12009=1= (0.04)2009 ×(25)2009 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2009×[(-5)2009]2思维延伸已知xm= ,xn=3.求下列各式的值:
(1)x m+n; (2) x2m?x2n; (3) x 3m+2n.解: (1) x m+n=x m?x n= ×3= ;
(2) x2m?x2n=(x m )2?(x n)2=( )2×32= × 9 = ;
(3) x 3m+2n=x3m?x2n=(x m)3?(x n)2=( )3×32
= × 9 = ☆ 理一理今天学习的知识同底数幂乘法幂的乘方(m,n都是正整数)1.幂的三个运算性质积的乘方2.学习了一种常见的数学方法把某个式子看作一个数或字母。 (整体思路) 再 见
字母表示:am·an=am+n ( m、n都为正整数)语言叙述:幂的乘方,底数不变,指数相乘。
字母表示:(am)n=amn (m,n都是正整数)
☆ 课前热身 1.2.1.剪一剪,想一想a2aa2.切一切,议一议☆ 探究活动 (一)(2a)2=4a2(2a) 3=8a3 2、比较下列各组算式的计算结果:
[2 ×(-3)]2 与 22 ×(-3)2 ;
[(-2)×(-5)]3与(-2)3 ×(-5)3
1、计算: (2×3)2与22 × 32,我们发现了什么? ∵ (2×3)2=62=36 ; 22 ×32=4×9=36
∴ (2×3)2 =22 × 32 都 相 等 ☆ 探究活动 (二) (1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.这两道题有什么特点?观察底数。底数为两个因式相乘,积的形式。我们学过的幂的运算性质适用吗?这种形式为积的乘方 ☆ 探究活动 (三) 同理:根据上述方法计算下列各题:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)积的乘方有什么规律呢?分组讨论积的乘方的运算性质:思考:积的乘方(ab)n =?一般地:n个n个n个即: 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(n为正整数)拓展: 当三个或三个以上因式的积乘方时, 也具有这一性质。 例如 (abc)n=anbncn例1:计算:
(1) (-3x)3 (2) (-5ab)2
(3) (xy2)2 (4) (-2xy3z2)4 解:(1)原式= (2)原式= (3)原式= (4)原式== -27x3=25a2b2 =x2y4=16x4y12z8(-3)3x3(-5)2a2b2x2(y2)2(-2)4x4(y3)4(z2)4能不能用积的乘方的性质计算?分析:以上各题底数都含有两个或两个以上的因式,我们运用积的乘方的运算性质。注意:
(1)负数乘方的符号法则。
(2)积的乘方等于积中“每一个”因式
乘方的积,防止有的因式漏乘方错误。
(3)在计算(-2xy3z2)4=(-2)4x4(y3)4(z2)4
=16x4y12z8的过程中,应把y3 , z2 看作一个数,再利用积的乘方性质进行计算。 思考: (-a)n= -an(n为正整数)对吗?当n为奇数时, (-a)n= -an(n为正整数)
当n为偶数时, (-a)n=an(n为正整数)
(体现了分类的思想)(1)(ab2)3=ab6 ( ) ×××(2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( )(4) -(-ab2)2=a2b4 ( )1、判断: √练一练2、计算:
(1) (ab)8 (2) (2m)3
(3) (-xy)5 (4) (5ab2)3
(5) (2×102)2 (6) (-3×103)3(2)8m3(3) –x5y5(4)125a3b6(5) 4×104(6) -27 ×109答案: (1)a8b8 3、计算:
(1)(-2x2y3)3 答案(2) 81a12b8c4答案 (1) -8x6y9(2) (-3a3b2c)41 计算: a3 ·a4· a+(a2)4+(-2a4)2解:原式=a3+4+1+a2×4+(-2)2 · (a4)2=a8+a8+4a8=6a8试一试:2 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除,最后算加减。=2x9-27x9+25x9=0一起探讨:(0.04)2009×[(-5)2009]2=?=(0.22)2009 × 54018=(0.2)4018 × 54008=(0.2 ×5)4018=14018解法一: (0.04)2009×[(-5)2009]2=1=(0.04)2009 × [(-5)2]2009=(0.04×25)2009=12009=1= (0.04)2009 ×(25)2009 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2009×[(-5)2009]2思维延伸已知xm= ,xn=3.求下列各式的值:
(1)x m+n; (2) x2m?x2n; (3) x 3m+2n.解: (1) x m+n=x m?x n= ×3= ;
(2) x2m?x2n=(x m )2?(x n)2=( )2×32= × 9 = ;
(3) x 3m+2n=x3m?x2n=(x m)3?(x n)2=( )3×32
= × 9 = ☆ 理一理今天学习的知识同底数幂乘法幂的乘方(m,n都是正整数)1.幂的三个运算性质积的乘方2.学习了一种常见的数学方法把某个式子看作一个数或字母。 (整体思路) 再 见
