第十一章 机械功与机械能 学情评估卷(含答案)沪粤版物理九年级上册
文档属性
| 名称 | 第十一章 机械功与机械能 学情评估卷(含答案)沪粤版物理九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 91.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-03-21 20:11:59 | ||
图片预览



文档简介
第十一章 机械功与机械能 学情评估
一、填空题(每空2分,共20分)
1.如图所示,当足球离开同学的脚后,足球在空中下落过程中,重力对足球________(填“做”或“没有做”)功。
2.2024年10月30日,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心点火发射,并取得圆满成功。点火后,火箭在加速上升的过程中,机械能________(填“变大”“变小”或“不变”)。
3.在课外实践活动中,小明用如图所示的装置拉动放在水平地面上的物块,已知拉力F=5 N,物块匀速前进4 m,则拉力F做的功为________J。
4.在体育考试中,小明投出的实心球在空中的运动轨迹如图所示。若实心球重20 N,从最高点到落地点的过程中,实心球下降的高度为2.7 m,用时0.75 s,则实心球下降过程中重力做功的功率为________W。
5.将一台功率为90 kW的发动机装到汽车上,汽车速度可达到108 km/h,若将该发动机装到汽船上,汽船的速度只能达到12 m/s,则汽车和汽船行驶时所受阻力之比为___________________________________________。
6.如图所示,在光滑的斜面上,将物体分别沿斜面AC和BC以相同的速度匀速拉到顶端C,做功的功率分别为P1、P2,则P1______(填“>”“<”或“=”)P2。
7.如图甲所示,用滑轮组将重为90 N的物体匀速提起,图乙是拉力F与绳子自由端移动距离s的关系图像,不计绳重和摩擦。则图乙中阴影部分的面积表示的物理量是________(填“总功”“有用功”或“额外功”)。
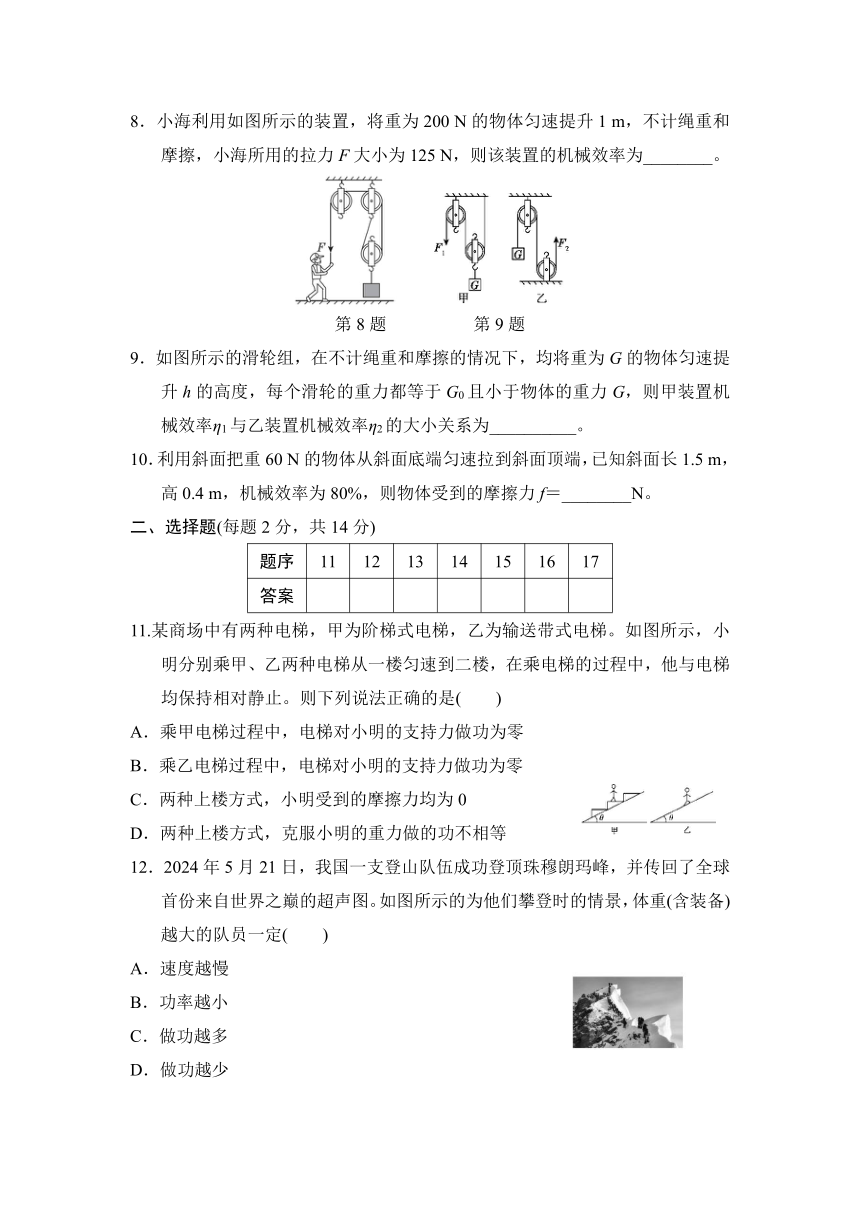
8.小海利用如图所示的装置,将重为200 N的物体匀速提升1 m,不计绳重和摩擦,小海所用的拉力F大小为125 N,则该装置的机械效率为________。
第8题 第9题
9.如图所示的滑轮组,在不计绳重和摩擦的情况下,均将重为G的物体匀速提升h的高度,每个滑轮的重力都等于G0且小于物体的重力G,则甲装置机械效率η1与乙装置机械效率η2的大小关系为__________。
10.利用斜面把重60 N的物体从斜面底端匀速拉到斜面顶端,已知斜面长1.5 m,高0.4 m,机械效率为80%,则物体受到的摩擦力f=________N。
二、选择题(每题2分,共14分)
题序 11 12 13 14 15 16 17
答案
11.某商场中有两种电梯,甲为阶梯式电梯,乙为输送带式电梯。如图所示,小明分别乘甲、乙两种电梯从一楼匀速到二楼,在乘电梯的过程中,他与电梯均保持相对静止。则下列说法正确的是( )
A.乘甲电梯过程中,电梯对小明的支持力做功为零
B.乘乙电梯过程中,电梯对小明的支持力做功为零
C.两种上楼方式,小明受到的摩擦力均为0
D.两种上楼方式,克服小明的重力做的功不相等
12.2024年5月21日,我国一支登山队伍成功登顶珠穆朗玛峰,并传回了全球首份来自世界之巅的超声图。如图所示的为他们攀登时的情景,体重(含装备)越大的队员一定( )
A.速度越慢
B.功率越小
C.做功越多
D.做功越少
13.八年级2班的小王同学用20 s的时间从教学楼一楼走到三楼,则他上楼消耗的功率最接近( )
A.1.8 W B.18 W
C.180 W D.1 800 W
14.高空抛物被称为“悬在城市上空的痛”,会给社会带来很大的危害。关于高空物体的下落过程中,下列分析正确的是( )
A.只受重力作用
B.动能越来越大
C.重力势能全部转化为动能
D.机械能总量保持不变
15.如图所示的是跳板跳水运动员跳水过程中的几个瞬间,不计空气阻力,其中①位置时运动员把跳板压到最低处。关于该过程,下列判断正确的是( )
A.①位置到②位置的过程中重力势能转化为弹性势能
B.②位置到③位置的过程中机械能不变
C.③位置时运动员的动能为零
D.③位置到④位置的过程中,动能主要转化为重力势能
16.如图所示,用质地均匀的杠杆匀速提升重物(不计摩擦),若想提高杠杆的机械效率,可采取的方法是( )
A.仅将物体悬挂点B向右移动,杠杆的机械效率增大
B.仅将物体悬挂点B向右移动,拉力所做的有用功减小
C.仅减小物体所受的重力,拉力所做的额外功减小
D.增加重物上升的高度,杠杆的机械效率增大
17.如图所示,物体A受到的重力是100 N,在拉力F的作用下,以0.2 m/s的速度在水平地面上向左做匀速直线运动。已知拉力F=5 N,滑轮组的机械效率为80%,则下列说法正确的是( )
A.5 s内拉力F所做功的大小是5 J
B.2 s内绳子自由端移动的距离是0.8 m
C.拉力F的功率是1 W
D.物体A受到水平地面的摩擦力大小是12 N
三、实验题(第18题4分,第19题4分,第20题10分,共18分)
18.如图所示,某同学在“探究动能的大小与哪些因素有关”的实验中,分别将A、B、C三个小球(mA=mB<mC)先后从同一装置的hA、hB、hC高度处(hA=hC>hB)由静止滚下,分别推动同一木盒运动一段距离后静止。
(1)小球到达水平面时,三个小球速度vA、vB、vC的大小关系是____________。
(2)在上述情景中,我们认为C球所具有的动能最大,依据是______________________________________________________。
19.某兴趣小组将一张硬卡片对折,在开口的一边剪两个小豁口A和B,然后套上橡皮筋,做成了一个会跳的卡片(如图所示)。
(1)小明将图中的卡片反过来,把它放在桌面上用手向下压,使橡皮筋伸长,迅速松开手,观察到卡片被弹起,这个现象说明:发生弹性形变的橡皮筋能对卡片________,因此它具有弹性势能。
(2)探究卡片跳起的高度与卡片质量是否有关,应选择质量不同的卡片,控制其他实验条件相同。操作中将卡片反过来,每次把它在桌面上用手压平的目的是__________________________。
20.某实验小组用如图所示的实验装置测量滑轮组的机械效率,其中每个滑轮的重力均为2 N,相关数据记录在下表中。
序号 钩码重G/N 钩码上升高度h/m 测力计的示数F/N 测力计移动的距离s/m 机械效率η/%
1 2 0.1 0.96 0.3 69.4
2 4 0.1 1.6 0.3 83.3
3 4 0.1 1.1 0.5
(1)在实验中,测绳端拉力F时,应尽量竖直向上________拉动弹簧测力计。
(2)通过分析表中数据可知,第3次实验使用的是______(填“甲”“乙”或“丙”)图所示的装置,且滑轮组的机械效率约为________。(保留一位小数)
(3)比较1、2两次实验,可得出的结论是:同一滑轮组,__________越大,机械效率越高。
(4)若将图甲中的滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率将______(填“变大”“变小”或“不变”)。
四、计算与推导题(第21题4分,第22题6分,第23题8分,共18分;解答要有必要的公式和过程)
21.如图所示的为某种型号的短途送货智能小车,该小车的质量m=600 kg。某次运送约100 kg的快递沿着厂区平直路线以36 km/h的速度匀速运动了1 000 m。该小车运动时受到的阻力为总重力的0.01。g取10 N/kg,求:
(1)该送货智能小车的牵引力;
(2)运送货物时该智能小车牵引力做功的功率。
22.如图所示,拉力F=80 N,物体所受重力G=192 N,经过t=10 s的时间,物体被匀速提高的距离h=4 m,不计滑轮与绳子间摩擦力以及绳重。
(1)求拉力做功的功率;
(2)求此时该滑轮组的机械效率;
(3)若绳子能承受的最大拉力为100 N,求此滑轮组能提升的最大物重。
23.如图所示,工人沿斜面用一定大小的推力F把一重为600 N的物体从斜面底部匀速推到顶部(不考虑物体的大小)。已知斜面长s=3 m,高h=1.5 m。
(1)若该过程中斜面的效率为60%,求工人所做的额外功。
(2)若斜面光滑没有摩擦,请分析说明随着斜面倾斜角度的增大,推力F的变化情况。
(3)若物体重力为G,与斜面之间的摩擦力为f,试根据有用功、额外功和总功之间的关系,证明F>f。
答案
一、1.做 2.变大 3.40 4.72 5.2∶5
6.< 7.总功 8.80% 9.η1<η2 10.4
二、11.B 12.C 13.C 14.B 15.B 16.A 17.D
三、18.(1)vA=vC>vB (2)C球把木盒推动的距离最远
19.(1)做功 (2)控制橡皮筋的形变量相同
20.(1)匀速 (2)丙;72.7% (3)钩码重力 (4)不变
四、21.解:(1)小车做匀速直线运动时,所受的牵引力等于阻力,(1分)
F=f=0.01G=0.01×mg=0.01×(600+100)kg×10 N/kg=70 N。(2分)
(2)小车的速度v=36× m/s=10 m/s,(1分)
由P===Fv得,
运送货物时该智能小车牵引力做功的功率P=Fv=70 N×10 m/s=700 W。(2分)
答题规范:①写出必要的文字说明;②正确写出原始公式、推导公式和解答过程;③计算结果要正确且有单位。(只有最后答案的不能得分)
22.解:(1)绳子承重股数n=3,绳子自由端移动距离
s=nh=3×4 m=12 m,
拉力做的功W总=Fs=80 N×12 m=960 J,
拉力做功的功率P===96 W。
(2)提升物体做的有用功W有用=Gh=192 N×4 m=768 J,
滑轮组的机械效率
η=×100%=×100%=80%。
(3)根据F=(G+G动)可得,动滑轮重G动=nF-G=3×80 N-192 N=48 N,
因绳子能承受的最大拉力为100 N,滑轮组能提升的最大物重G′=nF′-G动=3×100 N-48 N=252 N。
23.解:(1)该过程所做的有用功W有用=Gh=600 N×1.5 m=900 J;总功W总===1 500 J;该过程所做的额外功W额外=W总-W有用=1 500 J-900 J=600 J。
(2)若斜面光滑没有摩擦,则有W总=W有用,即Fs=Gh,则有F=G·,当斜面倾斜角度增大时,的值变大,G不变,F变大。
(3)推着物体在斜面上匀速运动时,推力F不仅要克服重力做功,还要克服摩擦力做功。
推力做的功为总功,W总=Fs;克服物体重力做的功为有用功,W有用=Gh,克服摩擦力做的功为额外功,W额外=fs;因为W总=W有用+W额外,所以W总>W额外,即Fs>fs,所以F>f。
一、填空题(每空2分,共20分)
1.如图所示,当足球离开同学的脚后,足球在空中下落过程中,重力对足球________(填“做”或“没有做”)功。
2.2024年10月30日,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心点火发射,并取得圆满成功。点火后,火箭在加速上升的过程中,机械能________(填“变大”“变小”或“不变”)。
3.在课外实践活动中,小明用如图所示的装置拉动放在水平地面上的物块,已知拉力F=5 N,物块匀速前进4 m,则拉力F做的功为________J。
4.在体育考试中,小明投出的实心球在空中的运动轨迹如图所示。若实心球重20 N,从最高点到落地点的过程中,实心球下降的高度为2.7 m,用时0.75 s,则实心球下降过程中重力做功的功率为________W。
5.将一台功率为90 kW的发动机装到汽车上,汽车速度可达到108 km/h,若将该发动机装到汽船上,汽船的速度只能达到12 m/s,则汽车和汽船行驶时所受阻力之比为___________________________________________。
6.如图所示,在光滑的斜面上,将物体分别沿斜面AC和BC以相同的速度匀速拉到顶端C,做功的功率分别为P1、P2,则P1______(填“>”“<”或“=”)P2。
7.如图甲所示,用滑轮组将重为90 N的物体匀速提起,图乙是拉力F与绳子自由端移动距离s的关系图像,不计绳重和摩擦。则图乙中阴影部分的面积表示的物理量是________(填“总功”“有用功”或“额外功”)。
8.小海利用如图所示的装置,将重为200 N的物体匀速提升1 m,不计绳重和摩擦,小海所用的拉力F大小为125 N,则该装置的机械效率为________。
第8题 第9题
9.如图所示的滑轮组,在不计绳重和摩擦的情况下,均将重为G的物体匀速提升h的高度,每个滑轮的重力都等于G0且小于物体的重力G,则甲装置机械效率η1与乙装置机械效率η2的大小关系为__________。
10.利用斜面把重60 N的物体从斜面底端匀速拉到斜面顶端,已知斜面长1.5 m,高0.4 m,机械效率为80%,则物体受到的摩擦力f=________N。
二、选择题(每题2分,共14分)
题序 11 12 13 14 15 16 17
答案
11.某商场中有两种电梯,甲为阶梯式电梯,乙为输送带式电梯。如图所示,小明分别乘甲、乙两种电梯从一楼匀速到二楼,在乘电梯的过程中,他与电梯均保持相对静止。则下列说法正确的是( )
A.乘甲电梯过程中,电梯对小明的支持力做功为零
B.乘乙电梯过程中,电梯对小明的支持力做功为零
C.两种上楼方式,小明受到的摩擦力均为0
D.两种上楼方式,克服小明的重力做的功不相等
12.2024年5月21日,我国一支登山队伍成功登顶珠穆朗玛峰,并传回了全球首份来自世界之巅的超声图。如图所示的为他们攀登时的情景,体重(含装备)越大的队员一定( )
A.速度越慢
B.功率越小
C.做功越多
D.做功越少
13.八年级2班的小王同学用20 s的时间从教学楼一楼走到三楼,则他上楼消耗的功率最接近( )
A.1.8 W B.18 W
C.180 W D.1 800 W
14.高空抛物被称为“悬在城市上空的痛”,会给社会带来很大的危害。关于高空物体的下落过程中,下列分析正确的是( )
A.只受重力作用
B.动能越来越大
C.重力势能全部转化为动能
D.机械能总量保持不变
15.如图所示的是跳板跳水运动员跳水过程中的几个瞬间,不计空气阻力,其中①位置时运动员把跳板压到最低处。关于该过程,下列判断正确的是( )
A.①位置到②位置的过程中重力势能转化为弹性势能
B.②位置到③位置的过程中机械能不变
C.③位置时运动员的动能为零
D.③位置到④位置的过程中,动能主要转化为重力势能
16.如图所示,用质地均匀的杠杆匀速提升重物(不计摩擦),若想提高杠杆的机械效率,可采取的方法是( )
A.仅将物体悬挂点B向右移动,杠杆的机械效率增大
B.仅将物体悬挂点B向右移动,拉力所做的有用功减小
C.仅减小物体所受的重力,拉力所做的额外功减小
D.增加重物上升的高度,杠杆的机械效率增大
17.如图所示,物体A受到的重力是100 N,在拉力F的作用下,以0.2 m/s的速度在水平地面上向左做匀速直线运动。已知拉力F=5 N,滑轮组的机械效率为80%,则下列说法正确的是( )
A.5 s内拉力F所做功的大小是5 J
B.2 s内绳子自由端移动的距离是0.8 m
C.拉力F的功率是1 W
D.物体A受到水平地面的摩擦力大小是12 N
三、实验题(第18题4分,第19题4分,第20题10分,共18分)
18.如图所示,某同学在“探究动能的大小与哪些因素有关”的实验中,分别将A、B、C三个小球(mA=mB<mC)先后从同一装置的hA、hB、hC高度处(hA=hC>hB)由静止滚下,分别推动同一木盒运动一段距离后静止。
(1)小球到达水平面时,三个小球速度vA、vB、vC的大小关系是____________。
(2)在上述情景中,我们认为C球所具有的动能最大,依据是______________________________________________________。
19.某兴趣小组将一张硬卡片对折,在开口的一边剪两个小豁口A和B,然后套上橡皮筋,做成了一个会跳的卡片(如图所示)。
(1)小明将图中的卡片反过来,把它放在桌面上用手向下压,使橡皮筋伸长,迅速松开手,观察到卡片被弹起,这个现象说明:发生弹性形变的橡皮筋能对卡片________,因此它具有弹性势能。
(2)探究卡片跳起的高度与卡片质量是否有关,应选择质量不同的卡片,控制其他实验条件相同。操作中将卡片反过来,每次把它在桌面上用手压平的目的是__________________________。
20.某实验小组用如图所示的实验装置测量滑轮组的机械效率,其中每个滑轮的重力均为2 N,相关数据记录在下表中。
序号 钩码重G/N 钩码上升高度h/m 测力计的示数F/N 测力计移动的距离s/m 机械效率η/%
1 2 0.1 0.96 0.3 69.4
2 4 0.1 1.6 0.3 83.3
3 4 0.1 1.1 0.5
(1)在实验中,测绳端拉力F时,应尽量竖直向上________拉动弹簧测力计。
(2)通过分析表中数据可知,第3次实验使用的是______(填“甲”“乙”或“丙”)图所示的装置,且滑轮组的机械效率约为________。(保留一位小数)
(3)比较1、2两次实验,可得出的结论是:同一滑轮组,__________越大,机械效率越高。
(4)若将图甲中的滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率将______(填“变大”“变小”或“不变”)。
四、计算与推导题(第21题4分,第22题6分,第23题8分,共18分;解答要有必要的公式和过程)
21.如图所示的为某种型号的短途送货智能小车,该小车的质量m=600 kg。某次运送约100 kg的快递沿着厂区平直路线以36 km/h的速度匀速运动了1 000 m。该小车运动时受到的阻力为总重力的0.01。g取10 N/kg,求:
(1)该送货智能小车的牵引力;
(2)运送货物时该智能小车牵引力做功的功率。
22.如图所示,拉力F=80 N,物体所受重力G=192 N,经过t=10 s的时间,物体被匀速提高的距离h=4 m,不计滑轮与绳子间摩擦力以及绳重。
(1)求拉力做功的功率;
(2)求此时该滑轮组的机械效率;
(3)若绳子能承受的最大拉力为100 N,求此滑轮组能提升的最大物重。
23.如图所示,工人沿斜面用一定大小的推力F把一重为600 N的物体从斜面底部匀速推到顶部(不考虑物体的大小)。已知斜面长s=3 m,高h=1.5 m。
(1)若该过程中斜面的效率为60%,求工人所做的额外功。
(2)若斜面光滑没有摩擦,请分析说明随着斜面倾斜角度的增大,推力F的变化情况。
(3)若物体重力为G,与斜面之间的摩擦力为f,试根据有用功、额外功和总功之间的关系,证明F>f。
答案
一、1.做 2.变大 3.40 4.72 5.2∶5
6.< 7.总功 8.80% 9.η1<η2 10.4
二、11.B 12.C 13.C 14.B 15.B 16.A 17.D
三、18.(1)vA=vC>vB (2)C球把木盒推动的距离最远
19.(1)做功 (2)控制橡皮筋的形变量相同
20.(1)匀速 (2)丙;72.7% (3)钩码重力 (4)不变
四、21.解:(1)小车做匀速直线运动时,所受的牵引力等于阻力,(1分)
F=f=0.01G=0.01×mg=0.01×(600+100)kg×10 N/kg=70 N。(2分)
(2)小车的速度v=36× m/s=10 m/s,(1分)
由P===Fv得,
运送货物时该智能小车牵引力做功的功率P=Fv=70 N×10 m/s=700 W。(2分)
答题规范:①写出必要的文字说明;②正确写出原始公式、推导公式和解答过程;③计算结果要正确且有单位。(只有最后答案的不能得分)
22.解:(1)绳子承重股数n=3,绳子自由端移动距离
s=nh=3×4 m=12 m,
拉力做的功W总=Fs=80 N×12 m=960 J,
拉力做功的功率P===96 W。
(2)提升物体做的有用功W有用=Gh=192 N×4 m=768 J,
滑轮组的机械效率
η=×100%=×100%=80%。
(3)根据F=(G+G动)可得,动滑轮重G动=nF-G=3×80 N-192 N=48 N,
因绳子能承受的最大拉力为100 N,滑轮组能提升的最大物重G′=nF′-G动=3×100 N-48 N=252 N。
23.解:(1)该过程所做的有用功W有用=Gh=600 N×1.5 m=900 J;总功W总===1 500 J;该过程所做的额外功W额外=W总-W有用=1 500 J-900 J=600 J。
(2)若斜面光滑没有摩擦,则有W总=W有用,即Fs=Gh,则有F=G·,当斜面倾斜角度增大时,的值变大,G不变,F变大。
(3)推着物体在斜面上匀速运动时,推力F不仅要克服重力做功,还要克服摩擦力做功。
推力做的功为总功,W总=Fs;克服物体重力做的功为有用功,W有用=Gh,克服摩擦力做的功为额外功,W额外=fs;因为W总=W有用+W额外,所以W总>W额外,即Fs>fs,所以F>f。
同课章节目录
- 第十一章 机械功与机械能
- 11.1 怎样才叫做功
- 11.2 怎样比较做功的快慢
- 11.3 如何提高机械效率
- 11.4 认识动能和势能
- 第十二章 内能与热机
- 12.1 认识内能
- 12.2 热量和热值
- 12.3 研究物质的比热容
- 12.4 热机与社会发展
- 第十三章 探究简单电路
- 13.1 从闪电谈起
- 13.2 电路的组成和连接方式
- 13.3 怎样认识和测量电流
- 13.4 探究串、并联电路中的电流
- 13.5 怎样认识和测量电压
- 13.6 探究串、并联电路中的电压
- 第十四章 探究欧姆定律
- 14.1 怎样认识电阻
- 14.2 探究欧姆定律
- 14.3 欧姆定律的应用
- 第十五章 电能与电功率
- 15.1 电能与电功
- 15.2 认识电功率
- 15.3 怎样使用电器正常工作
- 15.4 探究焦耳定律
