2025年数学中考专题一轮复习课件:4.22 解直角三角形的实际应用(共36张PPT)
文档属性
| 名称 | 2025年数学中考专题一轮复习课件:4.22 解直角三角形的实际应用(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 11:05:57 | ||
图片预览










文档简介
(共36张PPT)
2025年数学中考复习
4.22 解直角三角形的实际应用
基础知识
项目四 三角形
考点要求
壹
能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
核心知识点
贰
图示
仰角、俯角
在视线与水平线所成锐角中,视线在水平线上方的角叫作仰角,视线在水平线下方的角叫作俯角,如图1所示.
知识点1 解直角三角形的应用
方向角
一般指以观测者的位置为中心 ,将正北或者正南方向作为起始方向旋转到目标方向所成的角(一般指锐角 ),通常表达成北 (南)偏东 (西)度,如图3所示 ,点位于点的 ,点位于点 的 ,点位于点的北偏西45°方向 (或西北方向 ).
坡度 (坡比 )、坡角
坡面的铅直高度与水平宽度的比叫作坡度 (坡比 ),用字母表示 ;坡面与水平线的夹角叫作坡角.如图2所示,=.
北偏东方向30°
南偏东60°方向
求解各类直角三角形的实际问题的一般步骤:
(1)审题,把实际问题数据化,理清细节,由题意(或者原题图片)画出示意图;
(2)把示意图转化为几何图形;
(3)从欲求量所在的直角三角形开始,分析已知量与欲求量的联系,解直角三角形,若条件不足,转而先求所缺条件所在的直角三角形,然后返回,再去求第二次所缺条件的三角形,直至与已知条件或者已知定理挂上钩,最后层层返回;
(4)在解非直角三角形时,需要作垂线,构造直角三角形来解决.
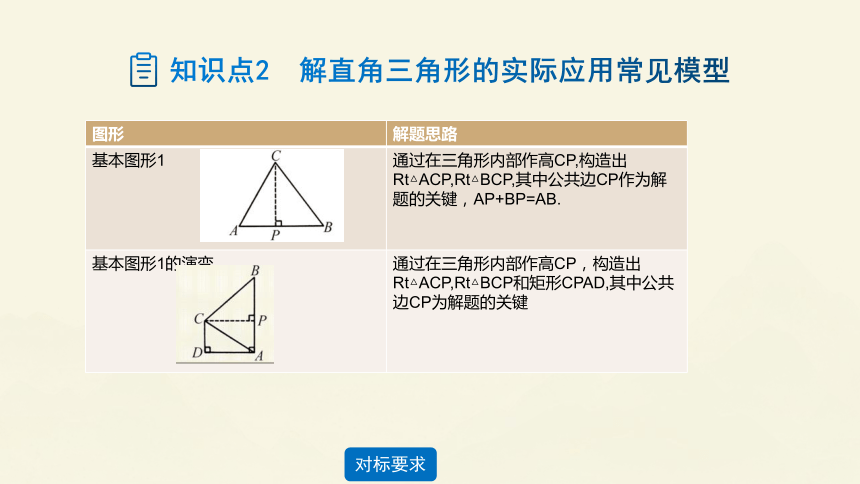
图形 解题思路
基本图形1 通过在三角形内部作高CP,构造出Rt△ACP,Rt△BCP,其中公共边CP作为解题的关键,AP+BP=AB.
基本图形1的演变 通过在三角形内部作高CP,构造出Rt△ACP,Rt△BCP和矩形CPAD,其中公共边CP为解题的关键
知识点2 解直角三角形的实际应用常见模型
基本图形2 通过在三角形外部作高BP,构造出Rt△ABP和Rt△BCP,其中公共边BP为解题的关键,AC+CP=AP.
基本图形2的演变(1) 延长DC交AB的延长线于点P,且AP⊥DP,构造出Rt△ACP和Rt△BDP.
基本图形2的演变(2) 过点A作AP⊥CD于点P,构造出Rt△ACP和矩形APDB,其中△CDB
为直角三角形.
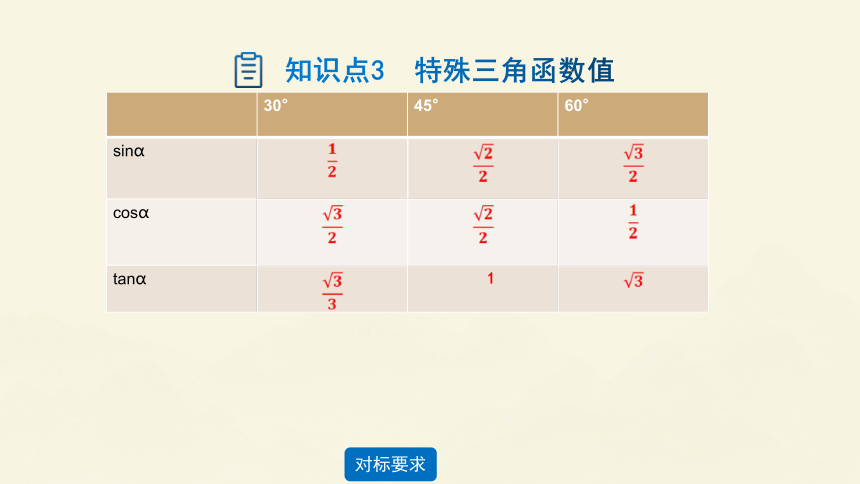
知识点3 特殊三角函数值
30° 45° 60°
sinɑ
cosɑ
tanɑ 1
考点攻坚
叁
(2022·长沙)如图所示,从楼顶 处看楼下荷塘处的俯角为45°,看楼下荷塘处的俯角为60°,已知楼高为30m,则荷塘的宽为 m(结果保留根号).
考点 实数的分类
例
【解析】
专项训练
肆
通关训练
1.(2022·百色)如图所示,某数学兴趣小组测量一棵树 的高度,在点处测得树顶 的仰角为45°,在点 处测得树顶 的仰角为60°,且三点在同一直线上,若16m,则这棵树 的高度是( )
A
A.8 B.8
C. 6 D.6
2.(2023·太原)如图所示,桔槔是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处,若已知:杠杆米,,支架,米,可以绕着点自由旋转,当点旋转到如图所示位置时,此时点到水平地面的距离为 米(结果保留根号).
提升训练
3.如图所示,一艘渔船位于小岛 的北偏东30°方向,距离小岛40nmile的点处,它沿着点 的南偏东15°的方向航行.
(1)渔船航行多远距离小岛 最近(结果保留根号)
(2)渔船到达距离小岛 最近点后,按原航向继续航行20nmile到点 处时突然发生事故,渔船马上向小岛上的救援队求救,问救援队从处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)
答案
3.
答案
2BM=40 nmile,故救援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是40 nmile.
课堂练习
伍
1.如图所示,从热气球看一栋楼底部的俯角是( )
D
A.∠BAD
B.∠ACB
C.∠BAC
D.∠DAC
2.(2022·崇左)如图所示,某博物馆大厅电梯的截面图中,的长为12米,与的夹角为,则高是( )
A
3.(2024·金华)某社区广场内,小颖和爸爸玩跷跷板,下图为跷跷板的简化图,其中长为5米,若它的一端着地,与水平地面所成的,则它的另一端到地面的距离为(A)
A. 5sinɑ米 B.5cosɑ米 C. 5tanɑ米 D. 米
4.(2021·青岛)如图所示,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为60°,建筑物底端的俯角为45°,点在同一平面内,斜坡的坡度.根据小颖的测量数据,计算出建筑物的高度约为( )(参考数据:3≈1.732)
A.136.6米 B.86.7米
C.186.7米 D.86.6米
A
5.(2024·云南)如图1是路灯维护工程车,图2是其工作示意图,工作篮底部与支撑平台平行,米.当,时,则工作篮底部到支撑平台的距离是 米.
6.(2023·湘潭)2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图所示,在发射的过程中,飞船从地面处发射,当飞船到达点时,从位于地面处的雷达站测得的距离是8km,仰角为30°;10s后飞船到达处,此时测得仰角为45°.
(1)求点离地面的高度;
(2)求飞船从处到处的平均速度(结果精确到0.1km/s,参考数据:3≈1.73)
答案
7.(2024·黄山)实验是培养学生创新能力的重要途径之一,如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处.已知试管,试管倾斜角为10°,经测得:21.7cm,8cm,145°
(1)求点的距离;
(2)实验时,当导气管紧贴水槽,延长的延长线于点,且(点在同一条直线上),求线段的长度.(结果精确到0.1,参考数据:10°≈0.17,10°≈0.98,10°≈0.18)
答案
答案
8.(2023·浙江)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2所示, 摄像头的仰角、俯角均为15°,摄像头高度cm,识别的最远水平距离cm.
(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点处,请问小杜最少需要下蹲多少厘米才能被识别
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗 请计算说明.
(精确到0.1cm,参考数据:
15°≈0.26,cos15°≈0.97,
tan15°≈0.27,sin20°≈ 0.34,
cos20°≈0.94,tan20°≈0.36)
答案
答案
谢谢观看
2025年数学中考复习
4.22 解直角三角形的实际应用
基础知识
项目四 三角形
考点要求
壹
能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
核心知识点
贰
图示
仰角、俯角
在视线与水平线所成锐角中,视线在水平线上方的角叫作仰角,视线在水平线下方的角叫作俯角,如图1所示.
知识点1 解直角三角形的应用
方向角
一般指以观测者的位置为中心 ,将正北或者正南方向作为起始方向旋转到目标方向所成的角(一般指锐角 ),通常表达成北 (南)偏东 (西)度,如图3所示 ,点位于点的 ,点位于点 的 ,点位于点的北偏西45°方向 (或西北方向 ).
坡度 (坡比 )、坡角
坡面的铅直高度与水平宽度的比叫作坡度 (坡比 ),用字母表示 ;坡面与水平线的夹角叫作坡角.如图2所示,=.
北偏东方向30°
南偏东60°方向
求解各类直角三角形的实际问题的一般步骤:
(1)审题,把实际问题数据化,理清细节,由题意(或者原题图片)画出示意图;
(2)把示意图转化为几何图形;
(3)从欲求量所在的直角三角形开始,分析已知量与欲求量的联系,解直角三角形,若条件不足,转而先求所缺条件所在的直角三角形,然后返回,再去求第二次所缺条件的三角形,直至与已知条件或者已知定理挂上钩,最后层层返回;
(4)在解非直角三角形时,需要作垂线,构造直角三角形来解决.
图形 解题思路
基本图形1 通过在三角形内部作高CP,构造出Rt△ACP,Rt△BCP,其中公共边CP作为解题的关键,AP+BP=AB.
基本图形1的演变 通过在三角形内部作高CP,构造出Rt△ACP,Rt△BCP和矩形CPAD,其中公共边CP为解题的关键
知识点2 解直角三角形的实际应用常见模型
基本图形2 通过在三角形外部作高BP,构造出Rt△ABP和Rt△BCP,其中公共边BP为解题的关键,AC+CP=AP.
基本图形2的演变(1) 延长DC交AB的延长线于点P,且AP⊥DP,构造出Rt△ACP和Rt△BDP.
基本图形2的演变(2) 过点A作AP⊥CD于点P,构造出Rt△ACP和矩形APDB,其中△CDB
为直角三角形.
知识点3 特殊三角函数值
30° 45° 60°
sinɑ
cosɑ
tanɑ 1
考点攻坚
叁
(2022·长沙)如图所示,从楼顶 处看楼下荷塘处的俯角为45°,看楼下荷塘处的俯角为60°,已知楼高为30m,则荷塘的宽为 m(结果保留根号).
考点 实数的分类
例
【解析】
专项训练
肆
通关训练
1.(2022·百色)如图所示,某数学兴趣小组测量一棵树 的高度,在点处测得树顶 的仰角为45°,在点 处测得树顶 的仰角为60°,且三点在同一直线上,若16m,则这棵树 的高度是( )
A
A.8 B.8
C. 6 D.6
2.(2023·太原)如图所示,桔槔是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处,若已知:杠杆米,,支架,米,可以绕着点自由旋转,当点旋转到如图所示位置时,此时点到水平地面的距离为 米(结果保留根号).
提升训练
3.如图所示,一艘渔船位于小岛 的北偏东30°方向,距离小岛40nmile的点处,它沿着点 的南偏东15°的方向航行.
(1)渔船航行多远距离小岛 最近(结果保留根号)
(2)渔船到达距离小岛 最近点后,按原航向继续航行20nmile到点 处时突然发生事故,渔船马上向小岛上的救援队求救,问救援队从处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)
答案
3.
答案
2BM=40 nmile,故救援队从B处出发沿点B的南偏东45°的方向航行到达事故地点航程最短,最短航程是40 nmile.
课堂练习
伍
1.如图所示,从热气球看一栋楼底部的俯角是( )
D
A.∠BAD
B.∠ACB
C.∠BAC
D.∠DAC
2.(2022·崇左)如图所示,某博物馆大厅电梯的截面图中,的长为12米,与的夹角为,则高是( )
A
3.(2024·金华)某社区广场内,小颖和爸爸玩跷跷板,下图为跷跷板的简化图,其中长为5米,若它的一端着地,与水平地面所成的,则它的另一端到地面的距离为(A)
A. 5sinɑ米 B.5cosɑ米 C. 5tanɑ米 D. 米
4.(2021·青岛)如图所示,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为60°,建筑物底端的俯角为45°,点在同一平面内,斜坡的坡度.根据小颖的测量数据,计算出建筑物的高度约为( )(参考数据:3≈1.732)
A.136.6米 B.86.7米
C.186.7米 D.86.6米
A
5.(2024·云南)如图1是路灯维护工程车,图2是其工作示意图,工作篮底部与支撑平台平行,米.当,时,则工作篮底部到支撑平台的距离是 米.
6.(2023·湘潭)2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图所示,在发射的过程中,飞船从地面处发射,当飞船到达点时,从位于地面处的雷达站测得的距离是8km,仰角为30°;10s后飞船到达处,此时测得仰角为45°.
(1)求点离地面的高度;
(2)求飞船从处到处的平均速度(结果精确到0.1km/s,参考数据:3≈1.73)
答案
7.(2024·黄山)实验是培养学生创新能力的重要途径之一,如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处.已知试管,试管倾斜角为10°,经测得:21.7cm,8cm,145°
(1)求点的距离;
(2)实验时,当导气管紧贴水槽,延长的延长线于点,且(点在同一条直线上),求线段的长度.(结果精确到0.1,参考数据:10°≈0.17,10°≈0.98,10°≈0.18)
答案
答案
8.(2023·浙江)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2所示, 摄像头的仰角、俯角均为15°,摄像头高度cm,识别的最远水平距离cm.
(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点处,请问小杜最少需要下蹲多少厘米才能被识别
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗 请计算说明.
(精确到0.1cm,参考数据:
15°≈0.26,cos15°≈0.97,
tan15°≈0.27,sin20°≈ 0.34,
cos20°≈0.94,tan20°≈0.36)
答案
答案
谢谢观看
同课章节目录
