华师大版数学八年级下册期中复习题三【精华】(含答案)
文档属性
| 名称 | 华师大版数学八年级下册期中复习题三【精华】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 416.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 20:17:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
华师大版数学八年级下册期中复习题三【精华】
一、单选题
1.(2024八上·济南期中)在中,的对边分别记为a,b,c,其中不能判定为直角三角形的是( )
A. B.
C. D.
2.(2024九上·南明期中)《九章算术》是我国传统数学中重要的著作之一,奠定了我国传统数学的基本框架.《九章算术》中记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一扇形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,问它的高与宽各是多少?若设矩形门宽为x尺,则依题意可列方程为(1丈=10尺,1尺=10寸)( )
A. B.
C. D.
3.(2024八下·九龙坡期末)若式子有意义,则x的取值范围是( )
A. B.且 C.且 D.
4.(2024九上·凉州开学考)下列由线段组成的三角形是直角三角形的是( )
A. B.
C. D.
5.(2024九下·南丹模拟)如图,在中,,,,为的角平分线,点F为上一动点,点G为的中点,连接,则的最小值是( )
A.2 B. C.4 D.
二、填空题
6.(2024八下·辽阳期中)已知在中,比小,则的度数为 .
7.(2024九上·简阳月考)当x 时,是二次根式.
8.(2024九上·泸县期中)如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD= .
9.(2022·越秀模拟)使 在实数范围内有意义的 应满足的条件是 .
10.(2023八下·武平期末)如图,边长为的正方形中,点是边上的动点(不与、重合),将沿所在直线折叠,得,连接,则长的最小值是 .
11.(2024九下·宿城月考)计算的结果是 .
三、计算题
12.(2024八下·云梦期末)计算:
(1);
(2).
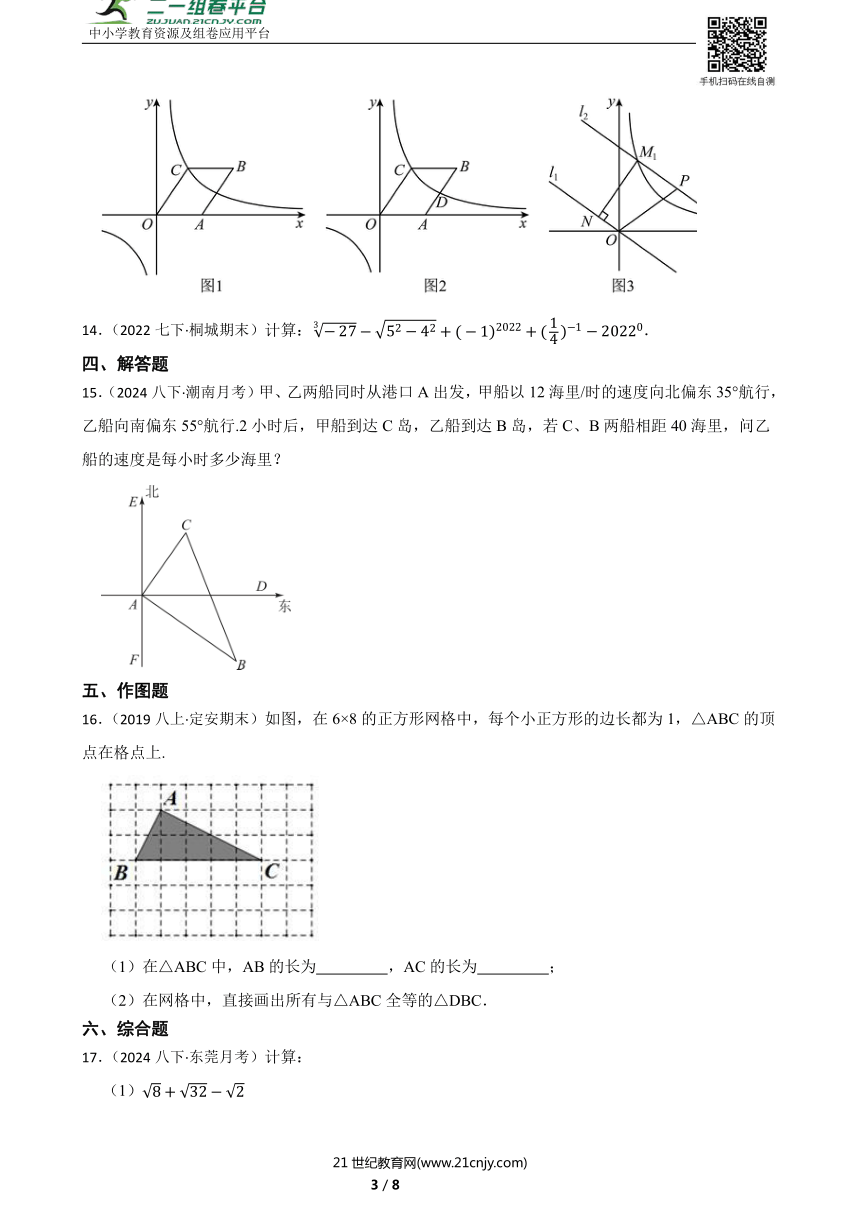
13.(2024九上·历城月考)【问题背景】在平面直角坐标系中,若两点分别为 ,则中点坐标为,如图1,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上,点B,C在第一象限,四边形 是平行四边形.
【构建联系】
若点C在反比例函数 的图象上,点C的横坐标为2,点B的纵坐标为3.
(1)求反比例函数的表达式;
(2)如图2,点D是边的中点,且在反比例函数图象上,求平行四边形的面积;
【深入探究】
(3)如图3,将直线:向上平移6个单位得到直线,直线与函数图象交于两点,点P为的中点,过点作于点N,请直接写出 P点坐标和的值.
14.(2022七下·桐城期末)计算:.
四、解答题
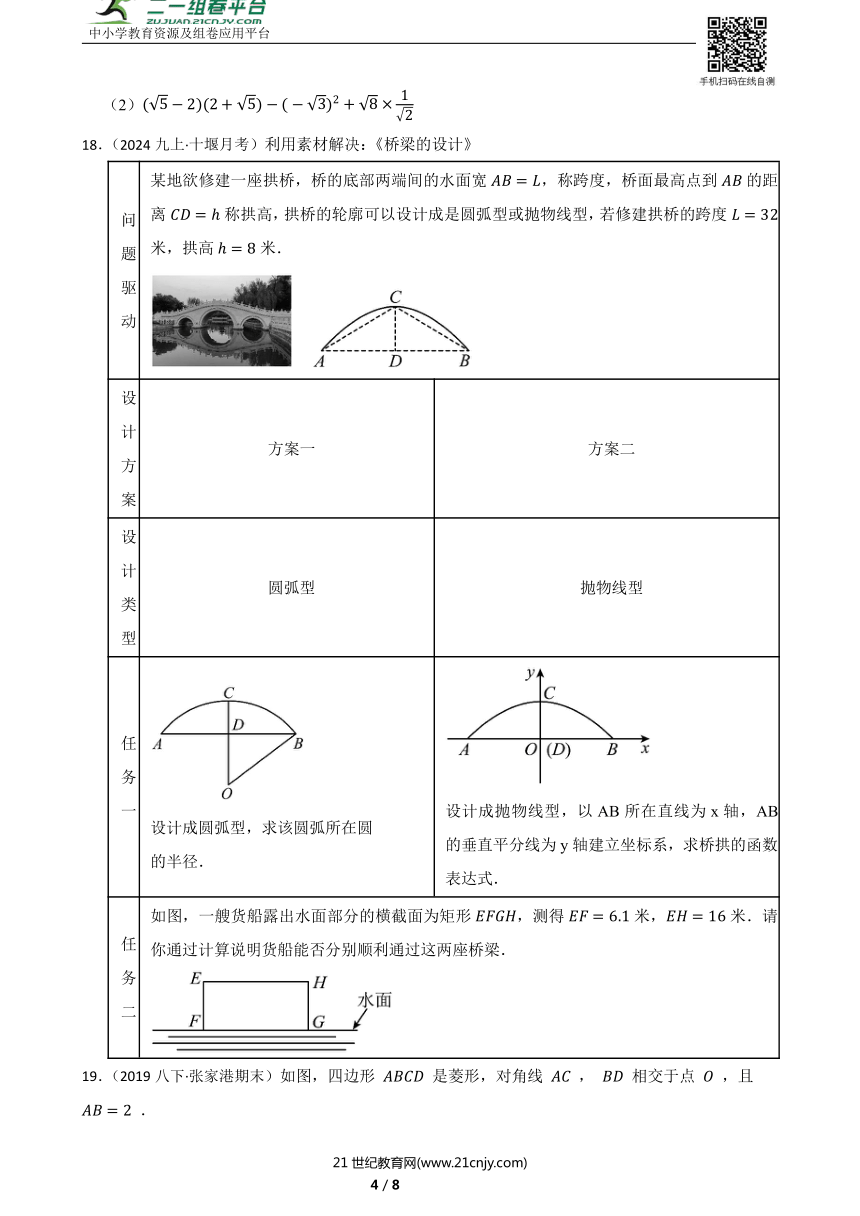
15.(2024八下·潮南月考)甲、乙两船同时从港口A出发,甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小时多少海里?
五、作图题
16.(2019八上·定安期末)如图,在6×8的正方形网格中,每个小正方形的边长都为1,△ABC的顶点在格点上.
(1)在△ABC中,AB的长为 ,AC的长为 ;
(2)在网格中,直接画出所有与△ABC全等的△DBC.
六、综合题
17.(2024八下·东莞月考)计算:
(1)
(2)
18.(2024九上·十堰月考)利用素材解决:《桥梁的设计》
问题驱动 某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
设计方案 方案一 方案二
设计类型 圆弧型 抛物线型
任务一 设计成圆弧型,求该圆弧所在圆 的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
任务二 如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
19.(2019八下·张家港期末)如图,四边形 是菱形,对角线 , 相交于点 ,且 .
(1)求菱形 的周长;
(2)若 ,求 的长.
七、实践探究题
20.(2024八下·拜城月考)下面是小文同学进行二次根式混合运算的过程,请认真阅读,完成相应的任务:
解: …第1步 …第2步 …第3步 …第4步
任务:
(1)上述解答过程中,第1步依据的乘法公式为 (用字母表示);
(2)上述解答过程,从第 步开始出错,具体的错误是 ;
(3)请计算正确的结果.
答案解析部分
1.【答案】C
【知识点】三角形内角和定理;勾股定理的逆定理
2.【答案】A
【知识点】勾股定理;一元二次方程的应用-几何问题
3.【答案】B
【知识点】分式有无意义的条件;二次根式有意义的条件;解一元一次不等式
4.【答案】C
【知识点】勾股定理的逆定理
5.【答案】B
【知识点】平行四边形的性质;解直角三角形;三角形的中位线定理
6.【答案】
【知识点】平行四边形的性质
7.【答案】≤;
【知识点】二次根式有意义的条件
8.【答案】
【知识点】勾股定理;旋转的性质
9.【答案】x≥1
【知识点】二次根式有意义的条件
10.【答案】
【知识点】三角形三边关系;勾股定理;正方形的性质
11.【答案】
【知识点】最简二次根式;二次根式的加减法
12.【答案】(1)解:
(2)解:
.
【知识点】二次根式的混合运算
13.【答案】(1)(2)9(3)
【知识点】待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;勾股定理;平行四边形的性质
14.【答案】解:原式=-3-3+1+4-1=-2.
【知识点】二次根式的定义;二次根式的混合运算;偶次方的非负性
15.【答案】乙船的速度是16海里/时.
【知识点】勾股定理的应用
16.【答案】(1);2
(2)如图,△D1BC、△D2BC、△D3BC 即为所求三角形.
【知识点】三角形全等及其性质;勾股定理
17.【答案】(1)解:原式=2 +4 -
=
(2)解:原式=(5-4)-3+2
=1-3+2
=0
【知识点】平方差公式及应用;二次根式的性质与化简
18.【答案】任务一:方案一,米;方案二,
任务二:方案一,能通过;方案二,不能通过
【知识点】勾股定理;垂径定理的实际应用;二次函数的实际应用-拱桥问题
19.【答案】(1)解:∵四边形ABCD是菱形,AB=2,∴菱形ABCD的周长为:8
(2)解:∵四边形ABCD是菱形,AC=2,AB=2
∴AC⊥BD,AO=1,∴BO ,∴BD=2
【知识点】勾股定理;菱形的性质
20.【答案】(1)(a+b)2=a2+2ab+b2
(2)3;的乘积计算错误
(3)原式 =25-2×2×6=1。
【知识点】二次根式的混合运算
21世纪教育网(www.21cnjy.com)
8 / 8
华师大版数学八年级下册期中复习题三【精华】
一、单选题
1.(2024八上·济南期中)在中,的对边分别记为a,b,c,其中不能判定为直角三角形的是( )
A. B.
C. D.
2.(2024九上·南明期中)《九章算术》是我国传统数学中重要的著作之一,奠定了我国传统数学的基本框架.《九章算术》中记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一扇形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,问它的高与宽各是多少?若设矩形门宽为x尺,则依题意可列方程为(1丈=10尺,1尺=10寸)( )
A. B.
C. D.
3.(2024八下·九龙坡期末)若式子有意义,则x的取值范围是( )
A. B.且 C.且 D.
4.(2024九上·凉州开学考)下列由线段组成的三角形是直角三角形的是( )
A. B.
C. D.
5.(2024九下·南丹模拟)如图,在中,,,,为的角平分线,点F为上一动点,点G为的中点,连接,则的最小值是( )
A.2 B. C.4 D.
二、填空题
6.(2024八下·辽阳期中)已知在中,比小,则的度数为 .
7.(2024九上·简阳月考)当x 时,是二次根式.
8.(2024九上·泸县期中)如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD= .
9.(2022·越秀模拟)使 在实数范围内有意义的 应满足的条件是 .
10.(2023八下·武平期末)如图,边长为的正方形中,点是边上的动点(不与、重合),将沿所在直线折叠,得,连接,则长的最小值是 .
11.(2024九下·宿城月考)计算的结果是 .
三、计算题
12.(2024八下·云梦期末)计算:
(1);
(2).
13.(2024九上·历城月考)【问题背景】在平面直角坐标系中,若两点分别为 ,则中点坐标为,如图1,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上,点B,C在第一象限,四边形 是平行四边形.
【构建联系】
若点C在反比例函数 的图象上,点C的横坐标为2,点B的纵坐标为3.
(1)求反比例函数的表达式;
(2)如图2,点D是边的中点,且在反比例函数图象上,求平行四边形的面积;
【深入探究】
(3)如图3,将直线:向上平移6个单位得到直线,直线与函数图象交于两点,点P为的中点,过点作于点N,请直接写出 P点坐标和的值.
14.(2022七下·桐城期末)计算:.
四、解答题
15.(2024八下·潮南月考)甲、乙两船同时从港口A出发,甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小时多少海里?
五、作图题
16.(2019八上·定安期末)如图,在6×8的正方形网格中,每个小正方形的边长都为1,△ABC的顶点在格点上.
(1)在△ABC中,AB的长为 ,AC的长为 ;
(2)在网格中,直接画出所有与△ABC全等的△DBC.
六、综合题
17.(2024八下·东莞月考)计算:
(1)
(2)
18.(2024九上·十堰月考)利用素材解决:《桥梁的设计》
问题驱动 某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
设计方案 方案一 方案二
设计类型 圆弧型 抛物线型
任务一 设计成圆弧型,求该圆弧所在圆 的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
任务二 如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
19.(2019八下·张家港期末)如图,四边形 是菱形,对角线 , 相交于点 ,且 .
(1)求菱形 的周长;
(2)若 ,求 的长.
七、实践探究题
20.(2024八下·拜城月考)下面是小文同学进行二次根式混合运算的过程,请认真阅读,完成相应的任务:
解: …第1步 …第2步 …第3步 …第4步
任务:
(1)上述解答过程中,第1步依据的乘法公式为 (用字母表示);
(2)上述解答过程,从第 步开始出错,具体的错误是 ;
(3)请计算正确的结果.
答案解析部分
1.【答案】C
【知识点】三角形内角和定理;勾股定理的逆定理
2.【答案】A
【知识点】勾股定理;一元二次方程的应用-几何问题
3.【答案】B
【知识点】分式有无意义的条件;二次根式有意义的条件;解一元一次不等式
4.【答案】C
【知识点】勾股定理的逆定理
5.【答案】B
【知识点】平行四边形的性质;解直角三角形;三角形的中位线定理
6.【答案】
【知识点】平行四边形的性质
7.【答案】≤;
【知识点】二次根式有意义的条件
8.【答案】
【知识点】勾股定理;旋转的性质
9.【答案】x≥1
【知识点】二次根式有意义的条件
10.【答案】
【知识点】三角形三边关系;勾股定理;正方形的性质
11.【答案】
【知识点】最简二次根式;二次根式的加减法
12.【答案】(1)解:
(2)解:
.
【知识点】二次根式的混合运算
13.【答案】(1)(2)9(3)
【知识点】待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;勾股定理;平行四边形的性质
14.【答案】解:原式=-3-3+1+4-1=-2.
【知识点】二次根式的定义;二次根式的混合运算;偶次方的非负性
15.【答案】乙船的速度是16海里/时.
【知识点】勾股定理的应用
16.【答案】(1);2
(2)如图,△D1BC、△D2BC、△D3BC 即为所求三角形.
【知识点】三角形全等及其性质;勾股定理
17.【答案】(1)解:原式=2 +4 -
=
(2)解:原式=(5-4)-3+2
=1-3+2
=0
【知识点】平方差公式及应用;二次根式的性质与化简
18.【答案】任务一:方案一,米;方案二,
任务二:方案一,能通过;方案二,不能通过
【知识点】勾股定理;垂径定理的实际应用;二次函数的实际应用-拱桥问题
19.【答案】(1)解:∵四边形ABCD是菱形,AB=2,∴菱形ABCD的周长为:8
(2)解:∵四边形ABCD是菱形,AC=2,AB=2
∴AC⊥BD,AO=1,∴BO ,∴BD=2
【知识点】勾股定理;菱形的性质
20.【答案】(1)(a+b)2=a2+2ab+b2
(2)3;的乘积计算错误
(3)原式 =25-2×2×6=1。
【知识点】二次根式的混合运算
21世纪教育网(www.21cnjy.com)
8 / 8
同课章节目录
