苏科版数学七年级下册期中复习题一【精华】(含答案)
文档属性
| 名称 | 苏科版数学七年级下册期中复习题一【精华】(含答案) | 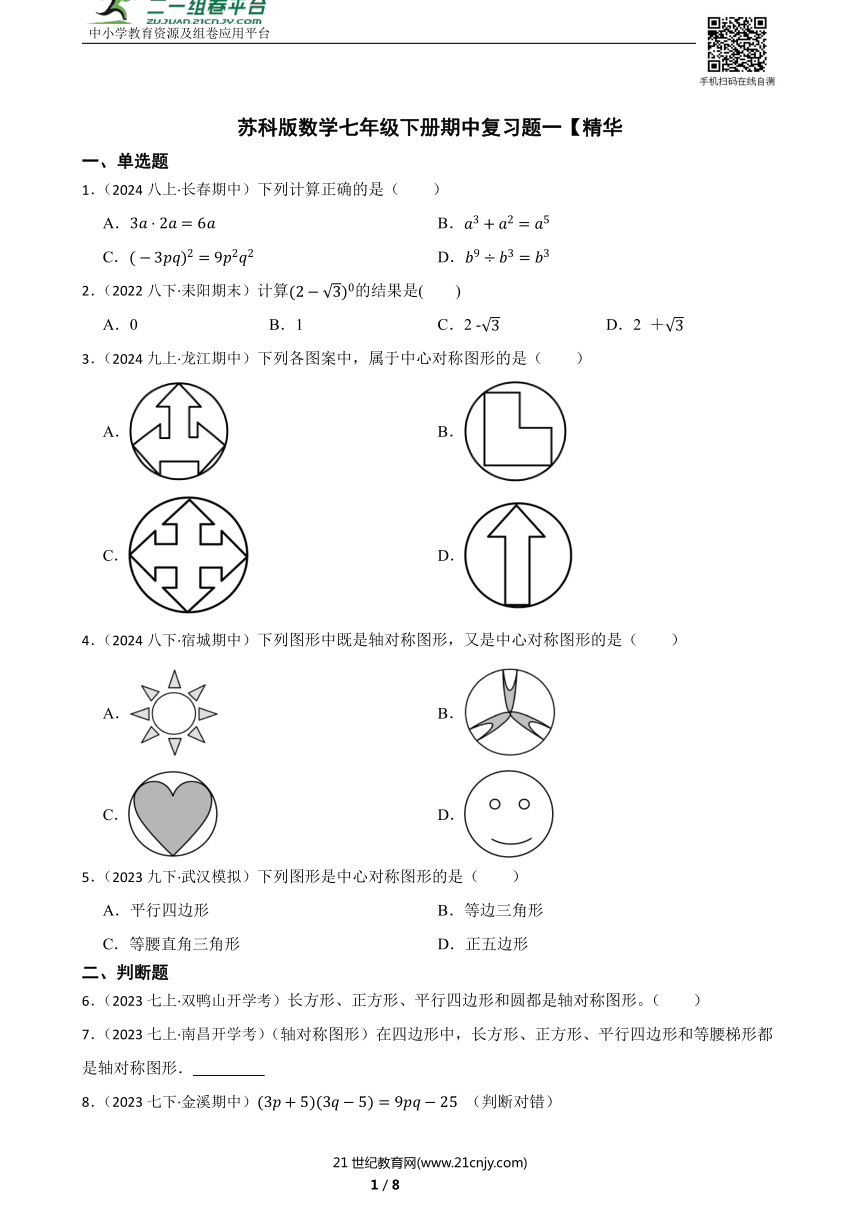 | |
| 格式 | docx | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 20:16:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏科版数学七年级下册期中复习题一【精华
一、单选题
1.(2024八上·长春期中)下列计算正确的是( )
A. B.
C. D.
2.(2022八下·耒阳期末)计算的结果是( )
A.0 B.1 C.2 - D.2 +
3.(2024九上·龙江期中)下列各图案中,属于中心对称图形的是( )
A. B.
C. D.
4.(2024八下·宿城期中)下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
5.(2023九下·武汉模拟)下列图形是中心对称图形的是( )
A.平行四边形 B.等边三角形
C.等腰直角三角形 D.正五边形
二、判断题
6.(2023七上·双鸭山开学考)长方形、正方形、平行四边形和圆都是轴对称图形。( )
7.(2023七上·南昌开学考)(轴对称图形)在四边形中,长方形、正方形、平行四边形和等腰梯形都是轴对称图形.
8.(2023七下·金溪期中) (判断对错)
9.3a4 (2a2﹣2a3)=6a8﹣6a12.(判断对错)
三、填空题
10.(2022八上·常德期末)2011年3月,英国和新加坡研究人员制造出观测极限为0.00000005米的光学显微镜,其中0.00000005米用科学记数法表示为 ;
11.(2023八下·汝阳期末)计算: .
12.计算a2(a﹣1)的结果等于 .
13.(2020七下·凌海期末)若4x=2,4y=3,则4x+y= 。
14.(2021九下·天津开学考)计算 的结果等于 .
15.(2024七上·重庆市期末)某种细胞的直径是米,将用科学记数法表示为 .
四、计算题
16.(2024七下·江都月考)由乘方的定义可知:(n个a相乘).观察下列算式回答问题:
,
,
.
(1)______.
(2)计算:.
17.(2024七下·未央期中)利用整式乘法公式计算
(1)
(2)
五、解答题
18.(2023七下·唐河期末)图①、图②、图③都是的正方形网格,每个小正方形顶点叫做格点.点A、B、C均在格点上,要求作一个多边形使这三个点在这个多边形的边(包括顶点)上,且多边形的顶点在格点上.
(1)在图①中作一个三角形,使它是轴对称图形.
(2)在图②中作一个四边形,使它只是中心对称图形.
(3)在图③中作一个四边形,使它既是轴对称图形又是中心对称图形.
19.(2024七下·甘州期中)定义一种新运算“*”: ,比如:.
(1)求的值;
(2)已知,请根据上述运算,求x的值.
六、综合题
20.(2024七下·余杭月考)如图所示,边长为的正方形中有一个边长为的小正方形,图是由图中阴影部分拼成的一个长方形,设图中阴影部分面积为,图中阴影部分面积为.
(1)请直接用含和的代数式表示________,________;写出利用图形的面积关系所得到的公式___________(用式子表达);
(2)应用公式计算:;
(3)应用公式计算:.
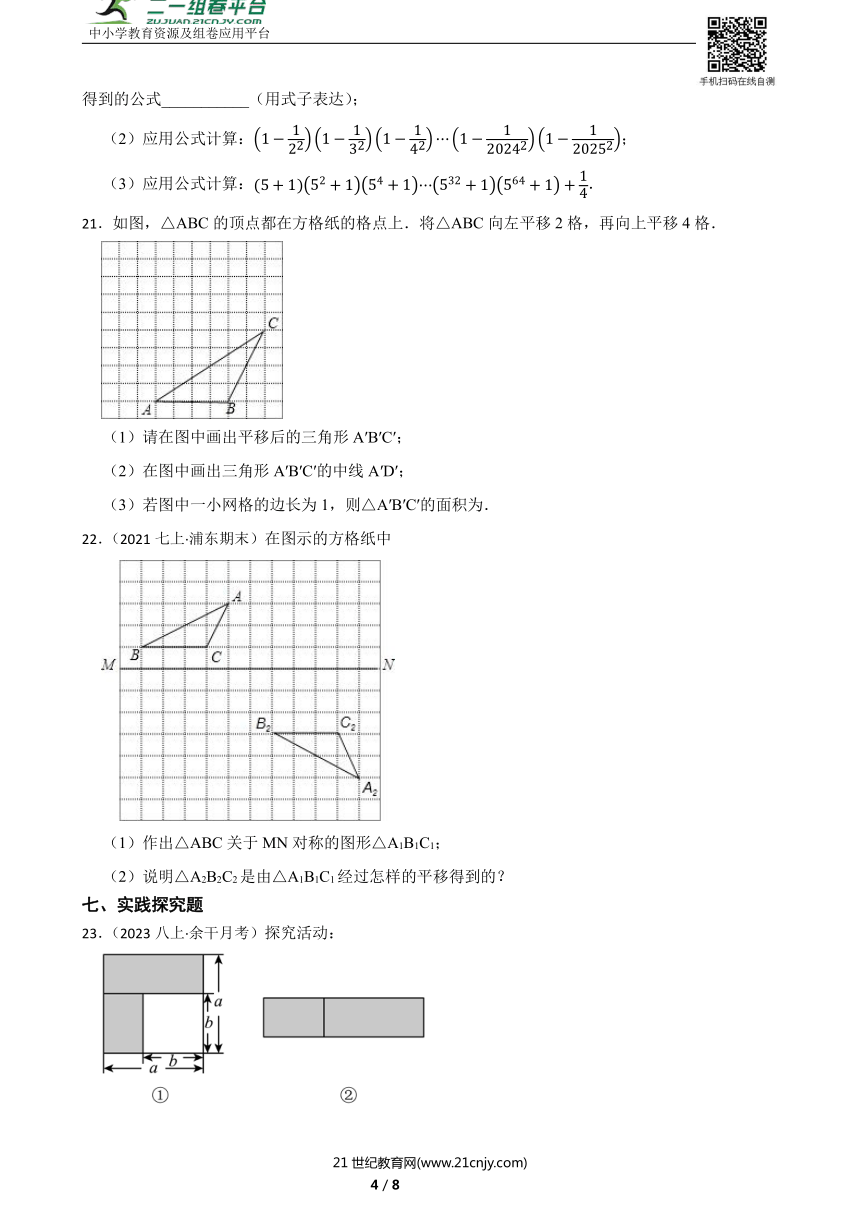
21.如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的三角形A′B′C′;
(2)在图中画出三角形A′B′C′的中线A′D′;
(3)若图中一小网格的边长为1,则△A′B′C′的面积为.
22.(2021七上·浦东期末)在图示的方格纸中
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
七、实践探究题
23.(2023八上·余干月考)探究活动:
(1)如图①,可以求出阴影部分的面积是 .(写成两数平方差的形式)
(2)如图②,若将阴影部分裁剪下来,重新拼成一个长方形,面积是 .(写成多项式乘法的形式)
(3)比较图①、图②阴影部分的面积,可以得到公式 .
答案解析部分
1.【答案】C
【知识点】同底数幂的除法;单项式乘单项式;合并同类项法则及应用;积的乘方运算
2.【答案】B
【知识点】零指数幂
3.【答案】C
【知识点】中心对称及中心对称图形
4.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】A
【知识点】中心对称及中心对称图形
6.【答案】错误
【知识点】轴对称图形
7.【答案】错
【知识点】轴对称图形
8.【答案】错误
【知识点】多项式乘多项式
9.【答案】错误
【知识点】单项式乘多项式
10.【答案】5×10-8
【知识点】科学记数法表示大于0且小于1的数
11.【答案】3
【知识点】零指数幂;负整数指数幂
12.【答案】a3﹣a2
【知识点】单项式乘多项式
13.【答案】6
【知识点】同底数幂的乘法
14.【答案】x6
【知识点】同底数幂的除法
15.【答案】
【知识点】科学记数法表示大于0且小于1的数
16.【答案】(1)
(2)
【知识点】同底数幂的乘法;积的乘方运算
17.【答案】(1)
(2)
【知识点】完全平方公式及运用;平方差公式及应用
18.【答案】(1)如图①.答案不唯一
(2)如图②.答案不唯一
(3)如图③.答案不唯一
【知识点】作图﹣轴对称;作图﹣中心对称
19.【答案】(1)
(2)
【知识点】同底数幂的乘法;负整数指数幂
20.【答案】(1);;
(2)
(3)
【知识点】平方差公式及应用;平方差公式的几何背景
21.【答案】(1)解:所作图形如图所示
(2)解:所作图形如图所示
(3)解:S△A′B′C′= ×4×4=8.
【知识点】作图﹣平移
22.【答案】(1)解:△A1B1C1如图所示
(2)解:向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位).
【知识点】作图﹣轴对称;作图﹣平移
23.【答案】(1)
(2)
(3)
【知识点】平方差公式的几何背景
21世纪教育网(www.21cnjy.com)
2 / 8
苏科版数学七年级下册期中复习题一【精华
一、单选题
1.(2024八上·长春期中)下列计算正确的是( )
A. B.
C. D.
2.(2022八下·耒阳期末)计算的结果是( )
A.0 B.1 C.2 - D.2 +
3.(2024九上·龙江期中)下列各图案中,属于中心对称图形的是( )
A. B.
C. D.
4.(2024八下·宿城期中)下列图形中既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
5.(2023九下·武汉模拟)下列图形是中心对称图形的是( )
A.平行四边形 B.等边三角形
C.等腰直角三角形 D.正五边形
二、判断题
6.(2023七上·双鸭山开学考)长方形、正方形、平行四边形和圆都是轴对称图形。( )
7.(2023七上·南昌开学考)(轴对称图形)在四边形中,长方形、正方形、平行四边形和等腰梯形都是轴对称图形.
8.(2023七下·金溪期中) (判断对错)
9.3a4 (2a2﹣2a3)=6a8﹣6a12.(判断对错)
三、填空题
10.(2022八上·常德期末)2011年3月,英国和新加坡研究人员制造出观测极限为0.00000005米的光学显微镜,其中0.00000005米用科学记数法表示为 ;
11.(2023八下·汝阳期末)计算: .
12.计算a2(a﹣1)的结果等于 .
13.(2020七下·凌海期末)若4x=2,4y=3,则4x+y= 。
14.(2021九下·天津开学考)计算 的结果等于 .
15.(2024七上·重庆市期末)某种细胞的直径是米,将用科学记数法表示为 .
四、计算题
16.(2024七下·江都月考)由乘方的定义可知:(n个a相乘).观察下列算式回答问题:
,
,
.
(1)______.
(2)计算:.
17.(2024七下·未央期中)利用整式乘法公式计算
(1)
(2)
五、解答题
18.(2023七下·唐河期末)图①、图②、图③都是的正方形网格,每个小正方形顶点叫做格点.点A、B、C均在格点上,要求作一个多边形使这三个点在这个多边形的边(包括顶点)上,且多边形的顶点在格点上.
(1)在图①中作一个三角形,使它是轴对称图形.
(2)在图②中作一个四边形,使它只是中心对称图形.
(3)在图③中作一个四边形,使它既是轴对称图形又是中心对称图形.
19.(2024七下·甘州期中)定义一种新运算“*”: ,比如:.
(1)求的值;
(2)已知,请根据上述运算,求x的值.
六、综合题
20.(2024七下·余杭月考)如图所示,边长为的正方形中有一个边长为的小正方形,图是由图中阴影部分拼成的一个长方形,设图中阴影部分面积为,图中阴影部分面积为.
(1)请直接用含和的代数式表示________,________;写出利用图形的面积关系所得到的公式___________(用式子表达);
(2)应用公式计算:;
(3)应用公式计算:.
21.如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的三角形A′B′C′;
(2)在图中画出三角形A′B′C′的中线A′D′;
(3)若图中一小网格的边长为1,则△A′B′C′的面积为.
22.(2021七上·浦东期末)在图示的方格纸中
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
七、实践探究题
23.(2023八上·余干月考)探究活动:
(1)如图①,可以求出阴影部分的面积是 .(写成两数平方差的形式)
(2)如图②,若将阴影部分裁剪下来,重新拼成一个长方形,面积是 .(写成多项式乘法的形式)
(3)比较图①、图②阴影部分的面积,可以得到公式 .
答案解析部分
1.【答案】C
【知识点】同底数幂的除法;单项式乘单项式;合并同类项法则及应用;积的乘方运算
2.【答案】B
【知识点】零指数幂
3.【答案】C
【知识点】中心对称及中心对称图形
4.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】A
【知识点】中心对称及中心对称图形
6.【答案】错误
【知识点】轴对称图形
7.【答案】错
【知识点】轴对称图形
8.【答案】错误
【知识点】多项式乘多项式
9.【答案】错误
【知识点】单项式乘多项式
10.【答案】5×10-8
【知识点】科学记数法表示大于0且小于1的数
11.【答案】3
【知识点】零指数幂;负整数指数幂
12.【答案】a3﹣a2
【知识点】单项式乘多项式
13.【答案】6
【知识点】同底数幂的乘法
14.【答案】x6
【知识点】同底数幂的除法
15.【答案】
【知识点】科学记数法表示大于0且小于1的数
16.【答案】(1)
(2)
【知识点】同底数幂的乘法;积的乘方运算
17.【答案】(1)
(2)
【知识点】完全平方公式及运用;平方差公式及应用
18.【答案】(1)如图①.答案不唯一
(2)如图②.答案不唯一
(3)如图③.答案不唯一
【知识点】作图﹣轴对称;作图﹣中心对称
19.【答案】(1)
(2)
【知识点】同底数幂的乘法;负整数指数幂
20.【答案】(1);;
(2)
(3)
【知识点】平方差公式及应用;平方差公式的几何背景
21.【答案】(1)解:所作图形如图所示
(2)解:所作图形如图所示
(3)解:S△A′B′C′= ×4×4=8.
【知识点】作图﹣平移
22.【答案】(1)解:△A1B1C1如图所示
(2)解:向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位).
【知识点】作图﹣轴对称;作图﹣平移
23.【答案】(1)
(2)
(3)
【知识点】平方差公式的几何背景
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
