湘教版数学八年级下册期中复习题一【精华】(含答案)
文档属性
| 名称 | 湘教版数学八年级下册期中复习题一【精华】(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 677.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版数学八年级下册期中复习题一【精华】
一、单选题
1.(2024九下·辽宁模拟)下列命题是真命题的是( )
A.如果,那么
B.边长为1,, 的三角形是直角三角形
C.两个锐角之和一定是钝角
D.对角线互相垂直的四边形是菱形
2.(2024九上·越秀期末)下列图形中,是中心对称图形的是( ).
A. B. C. D.
3.(2024八上·沙市区期中)如图,是的角平分线,于点E,,,则长是( )
A.3 B.4 C.6 D.5
4.(2024八下·中山期末)下列各组线段中,能够组成直角三角形的是( )
A.6,8,10 B.6,7,8 C.5,6,7 D.4,5,6
5.(2023·冷水滩模拟)如图,直线,的平分线交于点,若,则等于( )
A. B. C. D.
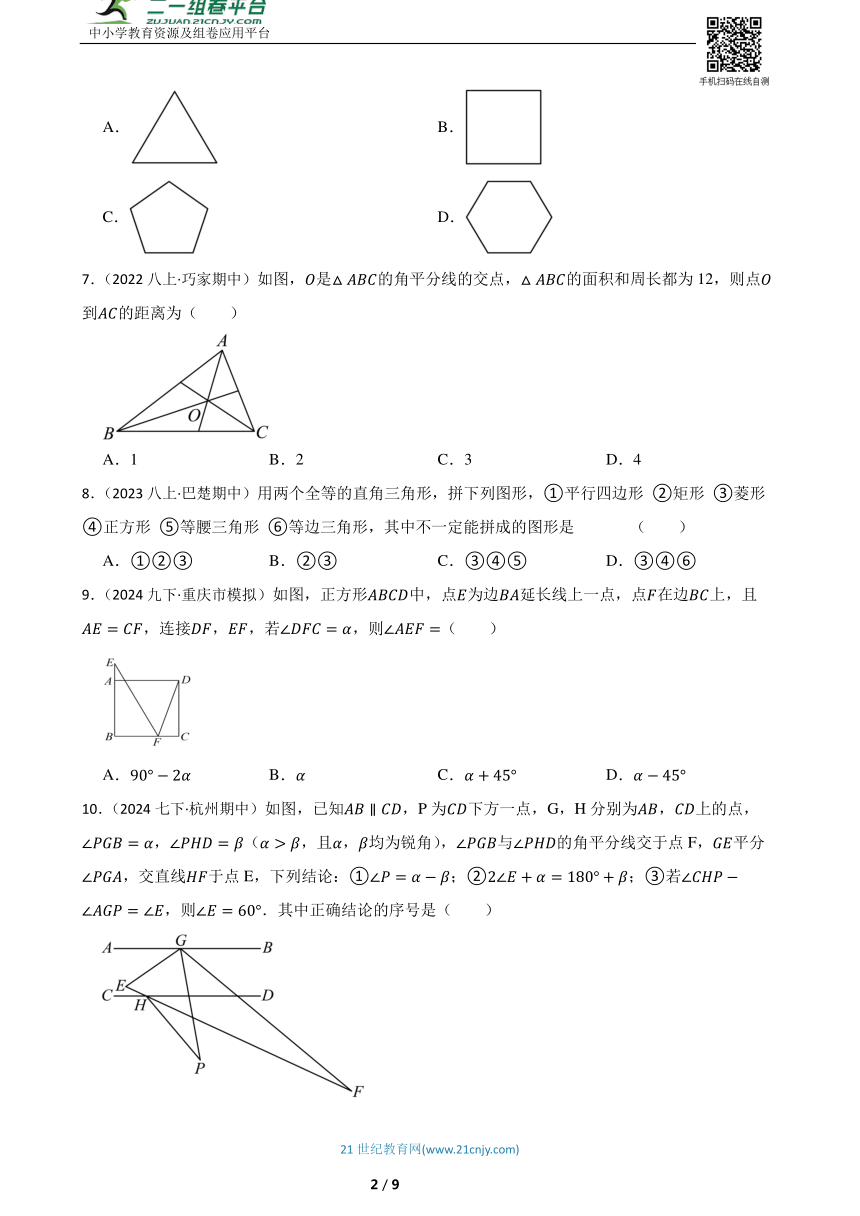
6.(2024八上·曲阜期末)下列图形中,内角和等于外角和的是( )
A. B.
C. D.
7.(2022八上·巧家期中)如图,是的角平分线的交点,的面积和周长都为12,则点到的距离为( )
A.1 B.2 C.3 D.4
8.(2023八上·巴楚期中)用两个全等的直角三角形,拼下列图形,①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形,其中不一定能拼成的图形是 ( )
A.①②③ B.②③ C.③④⑤ D.③④⑥
9.(2024九下·重庆市模拟)如图,正方形中,点为边延长线上一点,点在边上,且,连接,,若,则( )
A. B. C. D.
10.(2024七下·杭州期中)如图,已知,P为下方一点,G,H分别为,上的点,,(,且,均为锐角),与的角平分线交于点F,平分,交直线于点E,下列结论:①;②;③若,则.其中正确结论的序号是( )
A.①②③ B.②③ C.③ D.②
二、填空题
11.(2024八上·富裕期中)过五边形一个顶点的对角线共有 条.
12.(2024八上·南京期中)如图,两个阴影部分都是正方形,两个正方形的面积分别为36,64,则c的值为 .
13.(2024七上·沂源期中)如图,在中,CE平分∠ACB,CF平分外角∠ACD,且EF∥BC交AC 于M,若CM=5,则 .
14.如图,∠ABC=∠ADC=90°,E是AC的中点.若∠BDE=30°,则∠DBE的大小为 .
15.(2024八下·邹城期中)如图,在矩形中,边长,边长,对角线的垂直平分线分别与相交于点和相交于点O,动点分别从两点出发,分别绕和运动,点P的速度为,路径为.点Q的速度为,路径为两个动点返回起点后均停止运动.若点P和点Q同时出发,当四边形为平行四边形时,所用时间为 s.
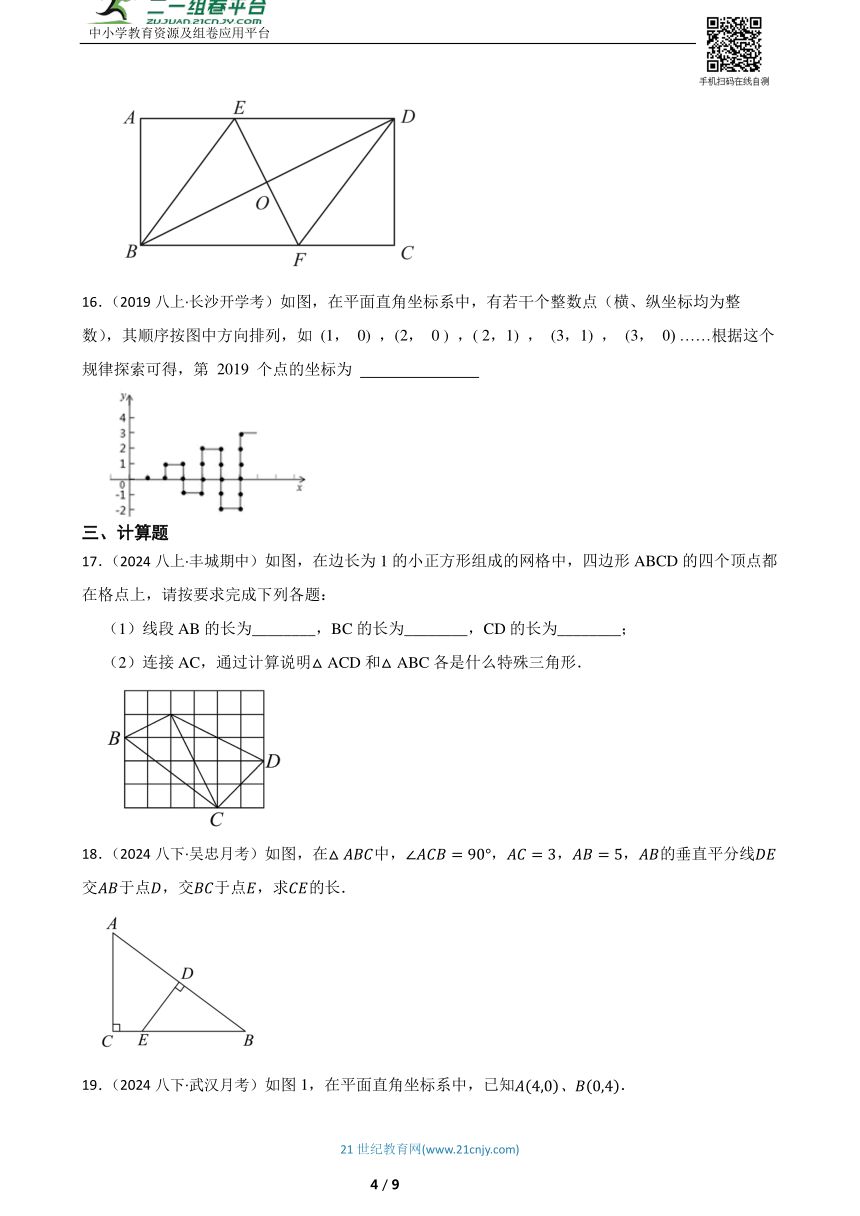
16.(2019八上·长沙开学考)如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如 (1, 0) ,(2, 0 ) ,( 2,1) , (3,1) , (3, 0) ……根据这个规律探索可得,第 2019 个点的坐标为
三、计算题
17.(2024八上·丰城期中)如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题:
(1)线段AB的长为________,BC的长为________,CD的长为________;
(2)连接AC,通过计算说明△ACD和△ABC各是什么特殊三角形.
18.(2024八下·吴忠月考)如图,在中,,,,的垂直平分线交于点,交于点,求的长.
19.(2024八下·武汉月考)如图1,在平面直角坐标系中,已知.
(1)如图1,若点在轴负半轴,使,则点坐标为________;
(2)如图2,若点在第二象限,,请用含字母表示;
(3)如图3,若点,点在轴的负半轴上,满足,求点的坐标.
四、解答题
20.(2024九上·吉林开学考)如图,长方形中,cm,cm,将此长方形折叠,使点B与点D重合,折痕为.求的面积.
21.(2025八上·梧州期末)如图,已知于D,于E,.
(1)求的长;
(2)求的度数.
22.(2024八下·陇县期中)如图,在 中, 是 边的中线, , , ,求 的度数.
23.(2023七下·长沙期末)如图,四边形中,,是的中点,平分.
(1)求证:平分;
(2)若,,求 的面积.
答案解析部分
1.【答案】B
【知识点】勾股定理的逆定理;菱形的判定;真命题与假命题
2.【答案】A
【知识点】中心对称及中心对称图形
3.【答案】A
【知识点】角平分线的性质
4.【答案】A
【知识点】勾股定理的逆定理
5.【答案】C
【知识点】角平分线的性质;内错角的概念;同旁内角的概念
6.【答案】B
【知识点】多边形内角与外角
7.【答案】B
【知识点】三角形的角平分线、中线和高;角平分线的性质
8.【答案】D
【知识点】等腰三角形的判定;等边三角形的判定;平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
9.【答案】D
【知识点】正方形的性质;三角形全等的判定-SAS
10.【答案】A
【知识点】平行线的性质;三角形的外角性质;角平分线的性质
11.【答案】2
【知识点】多边形的对角线
12.【答案】10
【知识点】勾股定理
13.【答案】100
【知识点】角平分线的性质;勾股定理
14.【答案】30°
【知识点】直角三角形斜边上的中线
15.【答案】
【知识点】三角形全等及其性质;线段垂直平分线的性质;勾股定理;菱形的判定与性质
16.【答案】(64,30)
【知识点】点的坐标;探索图形规律
17.【答案】(1),5,;(2)为等腰三角形,为直角三角形.
【知识点】等腰三角形的判定与性质;勾股定理;勾股定理的逆定理
18.【答案】
【知识点】线段垂直平分线的性质;勾股定理
19.【答案】(1)
(2)
(3)
【知识点】最简二次根式;坐标与图形性质;等腰三角形的判定与性质;勾股定理
20.【答案】
【知识点】勾股定理
21.【答案】(1)
(2)
【知识点】直角三角形全等的判定-HL
22.【答案】解:如图,∵ 是 边的中线, ,
∴ ,
, ,而 ,
∴由勾股定理的逆定理得: 是直角三角形,且 ,
∵又 ,
∴ ,
∵ 是 的邻补角,
∴ .
【知识点】三角形的角平分线、中线和高;勾股定理的逆定理
23.【答案】(1)证明:作垂足为,
平分,,,
,
,
,
,,
平分.
(2)解:由(1)可知:,
,,
.
【知识点】角平分线的性质;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 9
湘教版数学八年级下册期中复习题一【精华】
一、单选题
1.(2024九下·辽宁模拟)下列命题是真命题的是( )
A.如果,那么
B.边长为1,, 的三角形是直角三角形
C.两个锐角之和一定是钝角
D.对角线互相垂直的四边形是菱形
2.(2024九上·越秀期末)下列图形中,是中心对称图形的是( ).
A. B. C. D.
3.(2024八上·沙市区期中)如图,是的角平分线,于点E,,,则长是( )
A.3 B.4 C.6 D.5
4.(2024八下·中山期末)下列各组线段中,能够组成直角三角形的是( )
A.6,8,10 B.6,7,8 C.5,6,7 D.4,5,6
5.(2023·冷水滩模拟)如图,直线,的平分线交于点,若,则等于( )
A. B. C. D.
6.(2024八上·曲阜期末)下列图形中,内角和等于外角和的是( )
A. B.
C. D.
7.(2022八上·巧家期中)如图,是的角平分线的交点,的面积和周长都为12,则点到的距离为( )
A.1 B.2 C.3 D.4
8.(2023八上·巴楚期中)用两个全等的直角三角形,拼下列图形,①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形,其中不一定能拼成的图形是 ( )
A.①②③ B.②③ C.③④⑤ D.③④⑥
9.(2024九下·重庆市模拟)如图,正方形中,点为边延长线上一点,点在边上,且,连接,,若,则( )
A. B. C. D.
10.(2024七下·杭州期中)如图,已知,P为下方一点,G,H分别为,上的点,,(,且,均为锐角),与的角平分线交于点F,平分,交直线于点E,下列结论:①;②;③若,则.其中正确结论的序号是( )
A.①②③ B.②③ C.③ D.②
二、填空题
11.(2024八上·富裕期中)过五边形一个顶点的对角线共有 条.
12.(2024八上·南京期中)如图,两个阴影部分都是正方形,两个正方形的面积分别为36,64,则c的值为 .
13.(2024七上·沂源期中)如图,在中,CE平分∠ACB,CF平分外角∠ACD,且EF∥BC交AC 于M,若CM=5,则 .
14.如图,∠ABC=∠ADC=90°,E是AC的中点.若∠BDE=30°,则∠DBE的大小为 .
15.(2024八下·邹城期中)如图,在矩形中,边长,边长,对角线的垂直平分线分别与相交于点和相交于点O,动点分别从两点出发,分别绕和运动,点P的速度为,路径为.点Q的速度为,路径为两个动点返回起点后均停止运动.若点P和点Q同时出发,当四边形为平行四边形时,所用时间为 s.
16.(2019八上·长沙开学考)如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如 (1, 0) ,(2, 0 ) ,( 2,1) , (3,1) , (3, 0) ……根据这个规律探索可得,第 2019 个点的坐标为
三、计算题
17.(2024八上·丰城期中)如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题:
(1)线段AB的长为________,BC的长为________,CD的长为________;
(2)连接AC,通过计算说明△ACD和△ABC各是什么特殊三角形.
18.(2024八下·吴忠月考)如图,在中,,,,的垂直平分线交于点,交于点,求的长.
19.(2024八下·武汉月考)如图1,在平面直角坐标系中,已知.
(1)如图1,若点在轴负半轴,使,则点坐标为________;
(2)如图2,若点在第二象限,,请用含字母表示;
(3)如图3,若点,点在轴的负半轴上,满足,求点的坐标.
四、解答题
20.(2024九上·吉林开学考)如图,长方形中,cm,cm,将此长方形折叠,使点B与点D重合,折痕为.求的面积.
21.(2025八上·梧州期末)如图,已知于D,于E,.
(1)求的长;
(2)求的度数.
22.(2024八下·陇县期中)如图,在 中, 是 边的中线, , , ,求 的度数.
23.(2023七下·长沙期末)如图,四边形中,,是的中点,平分.
(1)求证:平分;
(2)若,,求 的面积.
答案解析部分
1.【答案】B
【知识点】勾股定理的逆定理;菱形的判定;真命题与假命题
2.【答案】A
【知识点】中心对称及中心对称图形
3.【答案】A
【知识点】角平分线的性质
4.【答案】A
【知识点】勾股定理的逆定理
5.【答案】C
【知识点】角平分线的性质;内错角的概念;同旁内角的概念
6.【答案】B
【知识点】多边形内角与外角
7.【答案】B
【知识点】三角形的角平分线、中线和高;角平分线的性质
8.【答案】D
【知识点】等腰三角形的判定;等边三角形的判定;平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
9.【答案】D
【知识点】正方形的性质;三角形全等的判定-SAS
10.【答案】A
【知识点】平行线的性质;三角形的外角性质;角平分线的性质
11.【答案】2
【知识点】多边形的对角线
12.【答案】10
【知识点】勾股定理
13.【答案】100
【知识点】角平分线的性质;勾股定理
14.【答案】30°
【知识点】直角三角形斜边上的中线
15.【答案】
【知识点】三角形全等及其性质;线段垂直平分线的性质;勾股定理;菱形的判定与性质
16.【答案】(64,30)
【知识点】点的坐标;探索图形规律
17.【答案】(1),5,;(2)为等腰三角形,为直角三角形.
【知识点】等腰三角形的判定与性质;勾股定理;勾股定理的逆定理
18.【答案】
【知识点】线段垂直平分线的性质;勾股定理
19.【答案】(1)
(2)
(3)
【知识点】最简二次根式;坐标与图形性质;等腰三角形的判定与性质;勾股定理
20.【答案】
【知识点】勾股定理
21.【答案】(1)
(2)
【知识点】直角三角形全等的判定-HL
22.【答案】解:如图,∵ 是 边的中线, ,
∴ ,
, ,而 ,
∴由勾股定理的逆定理得: 是直角三角形,且 ,
∵又 ,
∴ ,
∵ 是 的邻补角,
∴ .
【知识点】三角形的角平分线、中线和高;勾股定理的逆定理
23.【答案】(1)证明:作垂足为,
平分,,,
,
,
,
,,
平分.
(2)解:由(1)可知:,
,,
.
【知识点】角平分线的性质;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
