湘教版数学八年级下册期中复习题二【精华】(含答案)
文档属性
| 名称 | 湘教版数学八年级下册期中复习题二【精华】(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版数学八年级下册期中复习题二【精华】
一、单选题
1.(2022九上·江门期中)下列图标中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.(2024八下·梧州期中)下列选择中,是直角三角形的三边长的是( )
A.1,2,3 B.2,4,6 C.6,8,10 D.8,9,10
3.(2024·北京市模拟)下列图形是中心对称图形的是( )
A. B.
C. D.
4.(2024八下·顺平期末)如图,嘉琪想测量一座古塔的高度,在A处测得,再往前行进到达B处,测得,点 A,B,D在同一条直线上,根据测得的数据,这座古塔的高度为( )
A. B. C. D.
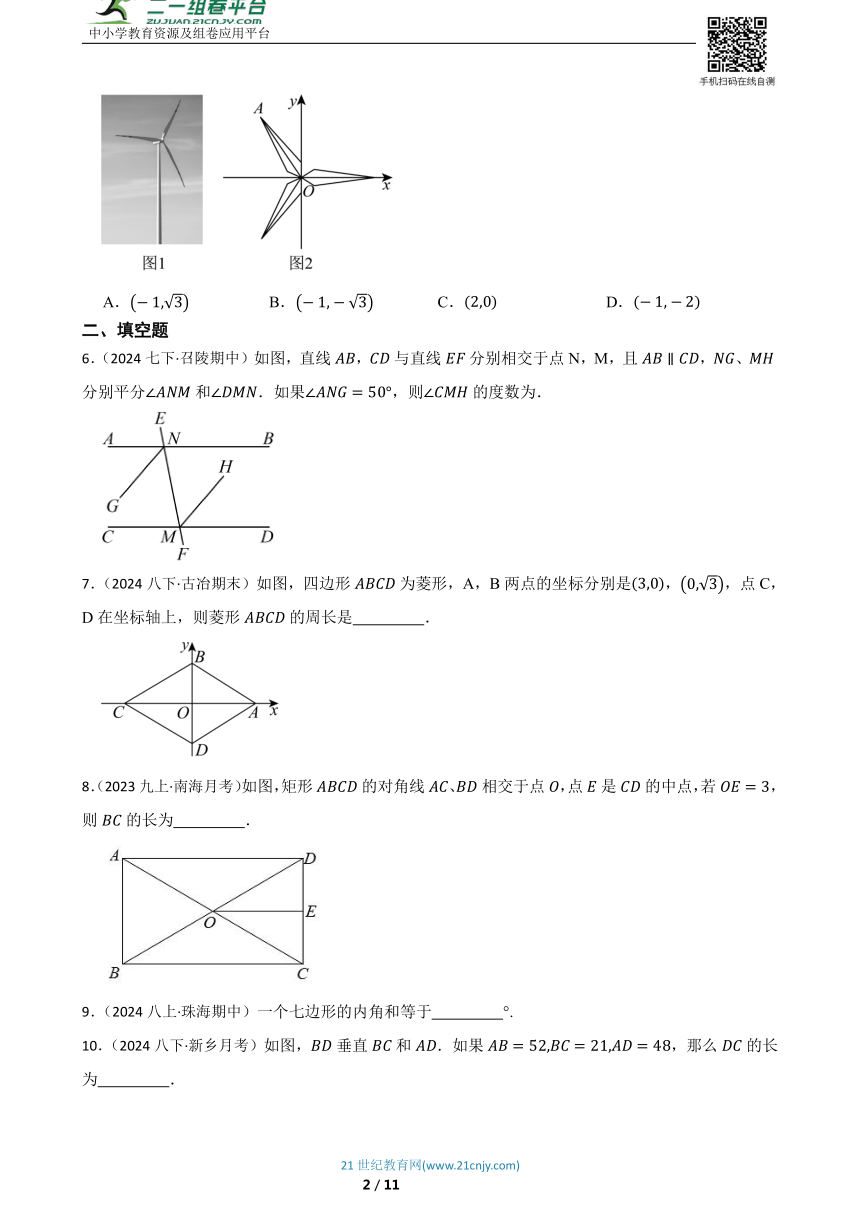
5.(2024八下·郑州期末)风力发电是一种将风能转化为电能的可再生能源技术.常见的风力发电机是由三片两两夹角的叶片底端相连组成(如图1).以扇叶重合处为坐标原点,水平方向为x轴建立平面直角坐标系(如图2),若某型号风力发电机的叶片每秒钟绕点O逆时针转动,点A初始位置横坐标为,与y轴正半轴夹角为,则第2024秒时,点A的坐标为( )
A. B. C. D.
二、填空题
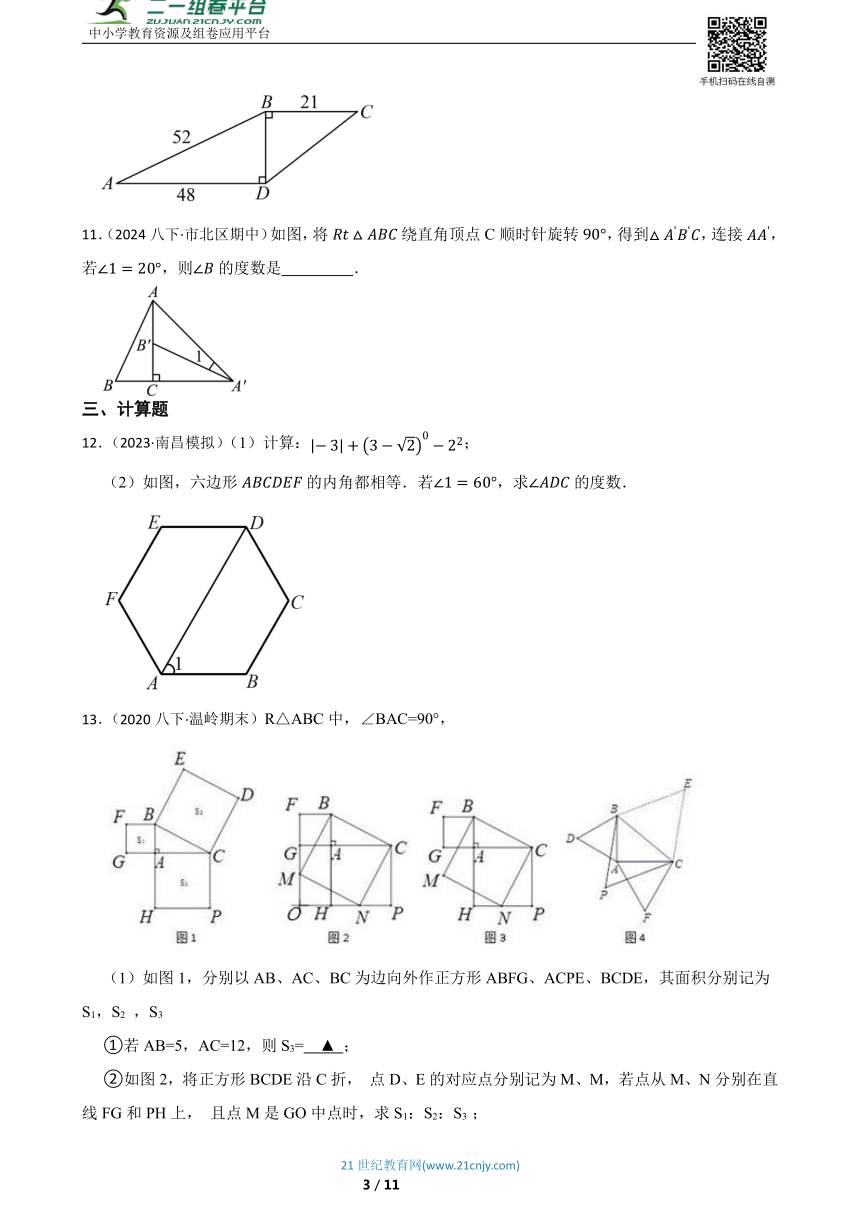
6.(2024七下·召陵期中)如图,直线,与直线分别相交于点N,M,且,、分别平分和.如果,则的度数为.
7.(2024八下·古冶期末)如图,四边形为菱形,A,B两点的坐标分别是,,点C,D在坐标轴上,则菱形的周长是 .
8.(2023九上·南海月考)如图,矩形的对角线、相交于点,点是的中点,若,则的长为 .
9.(2024八上·珠海期中)一个七边形的内角和等于 °.
10.(2024八下·新乡月考)如图,垂直和.如果,那么的长为 .
11.(2024八下·市北区期中)如图,将绕直角顶点C顺时针旋转,得到,连接,若,则的度数是 .
三、计算题
12.(2023·南昌模拟)(1)计算:;
(2)如图,六边形的内角都相等.若,求的度数.
13.(2020八下·温岭期末)R△ABC中,∠BAC=90°,
(1)如图1,分别以AB、AC、BC为边向外作正方形ABFG、ACPE、BCDE,其面积分别记为S1,S2 ,S3
①若AB=5,AC=12,则S3= ▲ ;
②如图2,将正方形BCDE沿C折, 点D、E的对应点分别记为M、M,若点从M、N分别在直线FG和PH上, 且点M是GO中点时,求S1:S2:S3 ;
③如图3,无论R△ABC三边长度如何变化,点M必定落在直线FG上吗 请说明理由;
(2)如图4,分别以AB, AC, BC为边向外作正三角形ABD, ACF, BCE, 再将三角形BCE沿BC翻折,点E的对应点记为P,若AB= 保持不变,随着AC的长度变化,点P也随之运动,试探究AP的值是否变化,若不变,直接写出AP的值;若改变,直接写出AP的最小值.
14.(2023八下·城厢开学考)材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2,那么.如何将双重二次根式化简?我们可以把转化为完全平方的形式,因此双重二次根式得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y')给出如下定义:若,则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).
请选择合适的材料解决下面的问题:
(1)点的“横负纵变点”为______,点的“横负纵变点”为______;
(2)化简:;
(3)已知a为常数(1≤a≤2),点M(,m)且,点是点M的“横负纵变点”,求点'的坐标.
四、解答题
15.(2024八下·崆峒期末)如图,某超市为了吸引顾客,在超市门口离地高的墙上,装有一个由传感器控制的门铃,人只要移至距该门铃及以内时,门铃就会自动发出语音“欢迎光临”,一名身高的学生走到处(),门铃恰好自动响起,即,则该学生此时与超市门口的水平距离长为多少米?
五、作图题
16.(2019八上·上海月考)尺规作图:如图,在直线MN上求作一点P,使点P到 ∠AOB两边的距离相等(不要求写出作法,但要保留作图痕迹,写出结论)
六、综合题
17.(2023八下·盐都月考)
(1)如图,以线段、为邻边,用尺规作图画出平行四边形保留作图痕迹,并说明它用了平行四边形的哪个判定方法?
(2)连接、,若,,,求平行四边形的面积.
18.(2023八下·礼泉期末)如图,在 ABCD中,E,F分别是AD,BC边上的点,且DE=CF,BE和AF的交点为M,CE和DF的交点为N,连接MN,EF.
(1)求证:四边形ABFE为平行四边形;
(2)若AD=6cm,求MN的长.
19.(2023八上·和平月考)学校计划种植一块草坪,形状为如图所示的四边形,其中,,,,.若每种植1平方米草坪成本为元,求学校种植该草坪的成本为多少.
七、实践探究题
20.(2024七上·张掖期末)探究归纳题:
【试验分析】
(1)如图①,经过点A可以作________条对角线;同样,经过点B可以作________条对角线;经过点C可以作________条对角线;经过点D可以作________条对角线.通过以上分析和总结,图①共有________条对角线;
【拓展延伸】
(2)运用(1)的分析方法,可得:图②共有条________对角线;图③共有________条对角线;
【探索归纳】
(3)对于n边形,共有________条对角线(用含n的代数式表示);
【特例验证】
(4)十边形共有________条对角线.
答案解析部分
1.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
2.【答案】C
【知识点】勾股定理的逆定理
3.【答案】B
【知识点】中心对称及中心对称图形
4.【答案】B
【知识点】三角形的外角性质;等腰三角形的判定与性质;含30°角的直角三角形
5.【答案】B
【知识点】点的坐标;含30°角的直角三角形;勾股定理
6.【答案】
【知识点】平行线的性质;角平分线的性质
7.【答案】
【知识点】最简二次根式;坐标与图形性质;勾股定理;菱形的性质
8.【答案】
【知识点】矩形的性质;三角形的中位线定理
9.【答案】900
【知识点】多边形内角与外角
10.【答案】
【知识点】勾股定理
11.【答案】
【知识点】旋转的性质;直角三角形的性质
12.【答案】(1)0;(2)
【知识点】零指数幂;多边形内角与外角;有理数混合运算法则(含乘方)
13.【答案】(1)解:①169
②设正方形ABGF的边长为a,则AB=BF=AG=FG=a,
∵正方形ABGF,正方形AHPC,∠BAC=90°,
∴∠AGO=∠GAH=∠AHO=90°
∴四边形AGOH是矩形,
∴∠F=∠NOM=90°,OG=AH
∵将正方形BCDE沿C折, 点D、E的对应点分别记为M、M
∴BM=MN,∠BMN=90°
∴∠BMF+∠NMO=90°,∠NMO+∠MNO=90°
∴∠BMF=∠MNO
在△BFM和△MON中
∴△BFM≌△MON(AAS)
∴OM=BF=a
∵点G是GO的中点,
∴OG=AH=2OM=2a,
∴正方形AHPC的边长为2a,
AB2+AC2=BC2
∴S12+S22=S32
∴S32=a2+4a2=5a2
∴ S1:S2:S3 =a2:4a2:5a2=1:4:5;
③过点M作MQ⊥HB于点Q,
∵正方形BCNM
∴BM=BC,∠BAC=∠MQB=90°,
∵∠MBQ+∠BMQ=90°,∠MBQ+∠ABC=90°,
∴∠BMQ=∠ABC
在△MBQ和△BCA中
∴△MBQ≌△BCA(AAS)
∴MQ=BA,
∵正方形ABFG,
∴AB=BF=AG,
∴FB=GA=MQ
∵BF∥AG∥MQ
∴点F、G、M三点共线即点M一定落在直线FG上.
(2)AP值会改变,AP最小值为
【知识点】矩形的判定与性质;正方形的性质;翻折变换(折叠问题);三角形全等的判定-SAS;三角形全等的判定-AAS
14.【答案】(1)(,);(,)
(2)+
(3)(﹣,﹣)
【知识点】完全平方公式及运用;分母有理化;二次根式的加减法;坐标与图形性质
15.【答案】
【知识点】勾股定理
16.【答案】解:根据题意,如图,作∠AOB的平分线,∠AOB的平分线与直线MN交于一点,则点P即为所求.
【知识点】角平分线的性质;尺规作图-作角的平分线
17.【答案】(1)解:如图:
结论:两组对边分别相等的四边形是平行四边形.
(2)解:如图:
设AC和BD交于点O,
四边形ABCD是平行四边形,
,,
,,
,,
,
,
,
,
.
【知识点】平行四边形的判定
18.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵DE=CF,
∴AE=BF.
∴四边形ABFE是平行四边形
(2)解:∵DE=CF,AD∥BC,
∴四边形DEFC是平行四边形,
∴DN=FN,
∵四边形ABFE是平行四边形,
∴AM=MF,
【知识点】平行四边形的性质;平行四边形的判定;三角形的中位线定理
19.【答案】学校种植该草坪的成本为元
【知识点】勾股定理;勾股定理的逆定理
20.【答案】(1)1,1,1,1,2;(2)5,9;(3);(4)35
【知识点】多边形的对角线
21世纪教育网(www.21cnjy.com)
1 / 11
湘教版数学八年级下册期中复习题二【精华】
一、单选题
1.(2022九上·江门期中)下列图标中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.(2024八下·梧州期中)下列选择中,是直角三角形的三边长的是( )
A.1,2,3 B.2,4,6 C.6,8,10 D.8,9,10
3.(2024·北京市模拟)下列图形是中心对称图形的是( )
A. B.
C. D.
4.(2024八下·顺平期末)如图,嘉琪想测量一座古塔的高度,在A处测得,再往前行进到达B处,测得,点 A,B,D在同一条直线上,根据测得的数据,这座古塔的高度为( )
A. B. C. D.
5.(2024八下·郑州期末)风力发电是一种将风能转化为电能的可再生能源技术.常见的风力发电机是由三片两两夹角的叶片底端相连组成(如图1).以扇叶重合处为坐标原点,水平方向为x轴建立平面直角坐标系(如图2),若某型号风力发电机的叶片每秒钟绕点O逆时针转动,点A初始位置横坐标为,与y轴正半轴夹角为,则第2024秒时,点A的坐标为( )
A. B. C. D.
二、填空题
6.(2024七下·召陵期中)如图,直线,与直线分别相交于点N,M,且,、分别平分和.如果,则的度数为.
7.(2024八下·古冶期末)如图,四边形为菱形,A,B两点的坐标分别是,,点C,D在坐标轴上,则菱形的周长是 .
8.(2023九上·南海月考)如图,矩形的对角线、相交于点,点是的中点,若,则的长为 .
9.(2024八上·珠海期中)一个七边形的内角和等于 °.
10.(2024八下·新乡月考)如图,垂直和.如果,那么的长为 .
11.(2024八下·市北区期中)如图,将绕直角顶点C顺时针旋转,得到,连接,若,则的度数是 .
三、计算题
12.(2023·南昌模拟)(1)计算:;
(2)如图,六边形的内角都相等.若,求的度数.
13.(2020八下·温岭期末)R△ABC中,∠BAC=90°,
(1)如图1,分别以AB、AC、BC为边向外作正方形ABFG、ACPE、BCDE,其面积分别记为S1,S2 ,S3
①若AB=5,AC=12,则S3= ▲ ;
②如图2,将正方形BCDE沿C折, 点D、E的对应点分别记为M、M,若点从M、N分别在直线FG和PH上, 且点M是GO中点时,求S1:S2:S3 ;
③如图3,无论R△ABC三边长度如何变化,点M必定落在直线FG上吗 请说明理由;
(2)如图4,分别以AB, AC, BC为边向外作正三角形ABD, ACF, BCE, 再将三角形BCE沿BC翻折,点E的对应点记为P,若AB= 保持不变,随着AC的长度变化,点P也随之运动,试探究AP的值是否变化,若不变,直接写出AP的值;若改变,直接写出AP的最小值.
14.(2023八下·城厢开学考)材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2,那么.如何将双重二次根式化简?我们可以把转化为完全平方的形式,因此双重二次根式得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y')给出如下定义:若,则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).
请选择合适的材料解决下面的问题:
(1)点的“横负纵变点”为______,点的“横负纵变点”为______;
(2)化简:;
(3)已知a为常数(1≤a≤2),点M(,m)且,点是点M的“横负纵变点”,求点'的坐标.
四、解答题
15.(2024八下·崆峒期末)如图,某超市为了吸引顾客,在超市门口离地高的墙上,装有一个由传感器控制的门铃,人只要移至距该门铃及以内时,门铃就会自动发出语音“欢迎光临”,一名身高的学生走到处(),门铃恰好自动响起,即,则该学生此时与超市门口的水平距离长为多少米?
五、作图题
16.(2019八上·上海月考)尺规作图:如图,在直线MN上求作一点P,使点P到 ∠AOB两边的距离相等(不要求写出作法,但要保留作图痕迹,写出结论)
六、综合题
17.(2023八下·盐都月考)
(1)如图,以线段、为邻边,用尺规作图画出平行四边形保留作图痕迹,并说明它用了平行四边形的哪个判定方法?
(2)连接、,若,,,求平行四边形的面积.
18.(2023八下·礼泉期末)如图,在 ABCD中,E,F分别是AD,BC边上的点,且DE=CF,BE和AF的交点为M,CE和DF的交点为N,连接MN,EF.
(1)求证:四边形ABFE为平行四边形;
(2)若AD=6cm,求MN的长.
19.(2023八上·和平月考)学校计划种植一块草坪,形状为如图所示的四边形,其中,,,,.若每种植1平方米草坪成本为元,求学校种植该草坪的成本为多少.
七、实践探究题
20.(2024七上·张掖期末)探究归纳题:
【试验分析】
(1)如图①,经过点A可以作________条对角线;同样,经过点B可以作________条对角线;经过点C可以作________条对角线;经过点D可以作________条对角线.通过以上分析和总结,图①共有________条对角线;
【拓展延伸】
(2)运用(1)的分析方法,可得:图②共有条________对角线;图③共有________条对角线;
【探索归纳】
(3)对于n边形,共有________条对角线(用含n的代数式表示);
【特例验证】
(4)十边形共有________条对角线.
答案解析部分
1.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
2.【答案】C
【知识点】勾股定理的逆定理
3.【答案】B
【知识点】中心对称及中心对称图形
4.【答案】B
【知识点】三角形的外角性质;等腰三角形的判定与性质;含30°角的直角三角形
5.【答案】B
【知识点】点的坐标;含30°角的直角三角形;勾股定理
6.【答案】
【知识点】平行线的性质;角平分线的性质
7.【答案】
【知识点】最简二次根式;坐标与图形性质;勾股定理;菱形的性质
8.【答案】
【知识点】矩形的性质;三角形的中位线定理
9.【答案】900
【知识点】多边形内角与外角
10.【答案】
【知识点】勾股定理
11.【答案】
【知识点】旋转的性质;直角三角形的性质
12.【答案】(1)0;(2)
【知识点】零指数幂;多边形内角与外角;有理数混合运算法则(含乘方)
13.【答案】(1)解:①169
②设正方形ABGF的边长为a,则AB=BF=AG=FG=a,
∵正方形ABGF,正方形AHPC,∠BAC=90°,
∴∠AGO=∠GAH=∠AHO=90°
∴四边形AGOH是矩形,
∴∠F=∠NOM=90°,OG=AH
∵将正方形BCDE沿C折, 点D、E的对应点分别记为M、M
∴BM=MN,∠BMN=90°
∴∠BMF+∠NMO=90°,∠NMO+∠MNO=90°
∴∠BMF=∠MNO
在△BFM和△MON中
∴△BFM≌△MON(AAS)
∴OM=BF=a
∵点G是GO的中点,
∴OG=AH=2OM=2a,
∴正方形AHPC的边长为2a,
AB2+AC2=BC2
∴S12+S22=S32
∴S32=a2+4a2=5a2
∴ S1:S2:S3 =a2:4a2:5a2=1:4:5;
③过点M作MQ⊥HB于点Q,
∵正方形BCNM
∴BM=BC,∠BAC=∠MQB=90°,
∵∠MBQ+∠BMQ=90°,∠MBQ+∠ABC=90°,
∴∠BMQ=∠ABC
在△MBQ和△BCA中
∴△MBQ≌△BCA(AAS)
∴MQ=BA,
∵正方形ABFG,
∴AB=BF=AG,
∴FB=GA=MQ
∵BF∥AG∥MQ
∴点F、G、M三点共线即点M一定落在直线FG上.
(2)AP值会改变,AP最小值为
【知识点】矩形的判定与性质;正方形的性质;翻折变换(折叠问题);三角形全等的判定-SAS;三角形全等的判定-AAS
14.【答案】(1)(,);(,)
(2)+
(3)(﹣,﹣)
【知识点】完全平方公式及运用;分母有理化;二次根式的加减法;坐标与图形性质
15.【答案】
【知识点】勾股定理
16.【答案】解:根据题意,如图,作∠AOB的平分线,∠AOB的平分线与直线MN交于一点,则点P即为所求.
【知识点】角平分线的性质;尺规作图-作角的平分线
17.【答案】(1)解:如图:
结论:两组对边分别相等的四边形是平行四边形.
(2)解:如图:
设AC和BD交于点O,
四边形ABCD是平行四边形,
,,
,,
,,
,
,
,
,
.
【知识点】平行四边形的判定
18.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵DE=CF,
∴AE=BF.
∴四边形ABFE是平行四边形
(2)解:∵DE=CF,AD∥BC,
∴四边形DEFC是平行四边形,
∴DN=FN,
∵四边形ABFE是平行四边形,
∴AM=MF,
【知识点】平行四边形的性质;平行四边形的判定;三角形的中位线定理
19.【答案】学校种植该草坪的成本为元
【知识点】勾股定理;勾股定理的逆定理
20.【答案】(1)1,1,1,1,2;(2)5,9;(3);(4)35
【知识点】多边形的对角线
21世纪教育网(www.21cnjy.com)
1 / 11
同课章节目录
