2025年数学中考专题一轮复习课件:5.25 菱形(共50张PPT)
文档属性
| 名称 | 2025年数学中考专题一轮复习课件:5.25 菱形(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 11:07:43 | ||
图片预览









文档简介
(共50张PPT)
2025年数学中考复习
5.25 菱形
基础知识
项目五 四边形
考点要求
壹
菱形
(1)理解掌握菱形的概念、性质及判定定理.
(2)会用菱形的有关知识进行证明,会计算菱形的面积.
核心知识点
贰
图形
菱形的性质
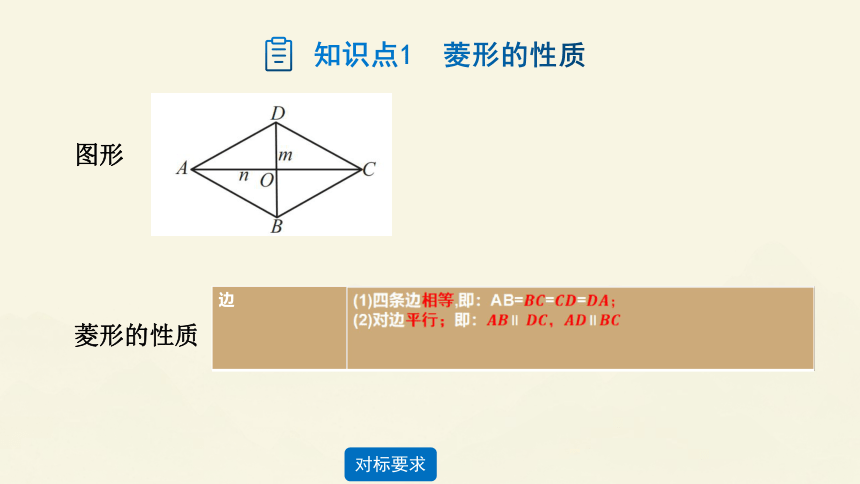
知识点1 菱形的性质
边 (1)四条边相等,即:AB===;
(2)对边平行;即:∥ ,∥
角 对角相等,即:=,=
对角线 (1)对角线互相垂直且平分,即:AC⊥BD,OA=
,OB=;
(2)对角线平分一组对角,即AC平分与
,BD平分 与
对称 性 菱形既是轴对称图形,又是中心对称图形,有两条对称轴.
(1)有一组 的平行四边形是菱形,即:在平行四边形 中, ,则四边形是菱形.
(2) 相等的四边形是菱形,即:四边形,则四边形是菱形.
(3)对角线 是菱形,即:在平行四边形 中,,则四边形是菱形.
知识点2 菱形的判定
邻边相等
四边
互相垂直的平行四边形
菱形的判定
知识点3 面积计算公式
利用平行四边形面积计算公式 S=底×高
利用对角线互桐垂直的性质计算 s=mn(m,n分别表示两条对角线的长)
考点攻坚
叁
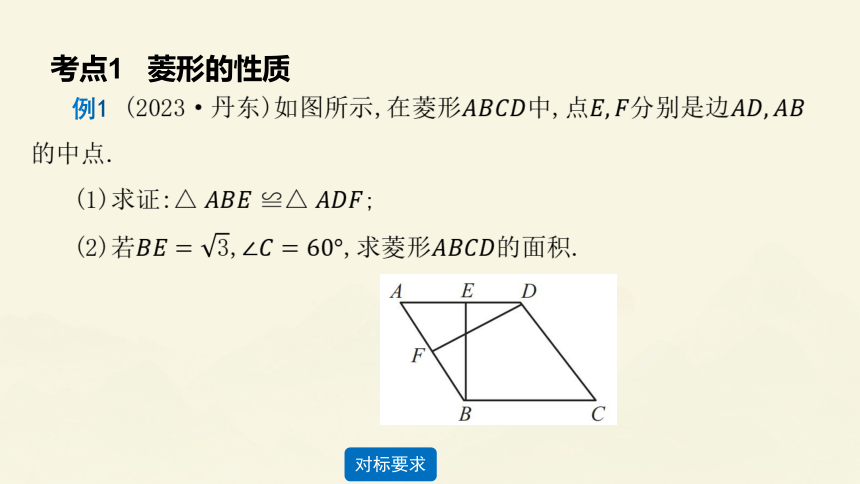
考点1 菱形的性质
例1
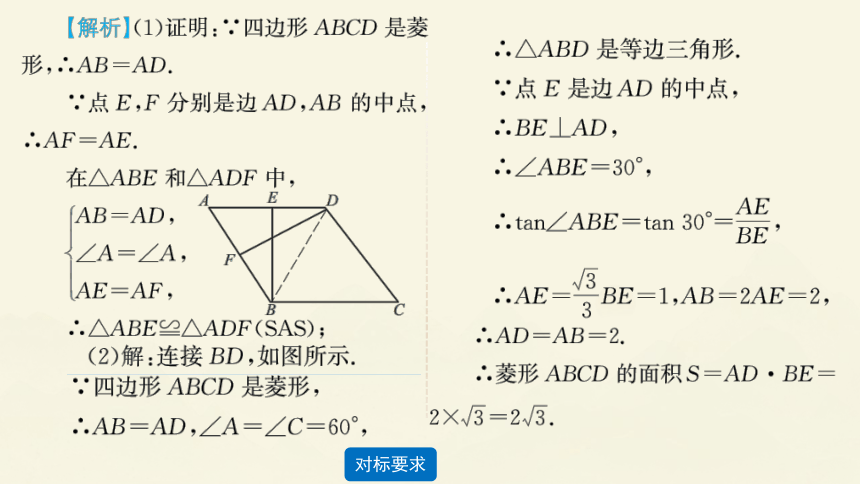
(2023·丹东)如图所示,在菱形中,点分别是边的中点.
(1)求证:;
(2)若,,求菱形的面积.
考点2 菱形的面积
例2
(2023·邵阳)如图所示,在矩形中,,相交于点,,.
(1)求证:四边形是菱形;
(2)若,,求的长及四边形的面积.
专项训练
肆
达标训练
1.(2022·百色)如图所示,在菱形中,对角线相交于点,下列结论中错误是(C )
A. B. C. D.
2.(2024·大理)如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形的周长为
cm.
8
3.如图所示,在菱形中,点,分别是边,的中点,若,,则的长是 .
1
4.菱形是一种富有美感的图形,小吴收到一块矩形的玉石,想尽可能制作成较大面积的菱形模型,在设计图纸上取作为这个菱形的对角线.
(1)请你用尺规作图的方法把这个菱形画出来(保留作图痕迹,不用写作法);
(2)利用(1)中尺规作图过程中提供的条件证明你所作的图形是菱形.
答案
5.(2022,南京)如图所示,在平行四边形中,点分别在上,且,连接且相交于点.
(1)求证:四边形是平行四边形;
(2)若,求四边形的面积.
答案
6.如图,在中,,分别是,的中点.
(1)求证:≌.
(2)连接,当线段与满足什么条件时,四边形是菱形 并说明理由.
答案
6.(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB,CD=AB,
∵E、F分别是边AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
在△ADE和△CBF中,AD=CB,AE=CF,∠A=∠C
∴△ADE≌△CBF(SAS).
答案
课堂练习
伍
1.(2024·安庆)下列条件中,能判定四边形是菱形的是(D)
A.对角线垂直
B.两对角线相等
C.两对角线互相平分
D.两对角线互相垂直平分
2.(2024·东莞)如图,四边形为菱形,于点,则的长为(B )
A.4 B.4.8 C.5 D.6
3.(2022·张家界)如图所示,菱形的对角线相交于点,过点作于点,连接,,若菱形的面积为32,则的长为( )
A.4
B.4
C.8
D.8
C
4.(2021·贵阳)如图所示,是菱形的一条对角线,点的延长线上,若,则的度数为 64° .
5.(2024·广西)如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形的周长为 cm.
8
6.(2024·泉州)如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为,则 25 .
7.(2022.怀化)如图所示,四边形是菱形,,是对角线 上的两点,且,连接,,,.
求证:四边形是菱形.
答案
7.证明:连接,交于点.∵四边形是菱形,,,.又,,即,是平行四边形.又,即,四边形是菱形.
8.(2022·承德)如图所示,在中,对角线相交于点,.
(1)求证:;
(2)若点分别为的中点,连接,,求的长及四边形的周长.
答案
8.(1)证明:∵四边形是平行四边形,,∴四边形是菱形,∴.
(2)解:∵点分别为的中点,∴的中位线,∴.∵,∴.∵四边形是菱形,∴.∵,在Rt中,,,∴,∴菱形的周长为.
9.(2024·淄博).如图,在菱形中,,,动点,分别在线段上,且,则的最小值为 .
10.(2024·江西模拟)如图,菱形的周长为40,对角线相交于点,若点的中点,则的长是 .
11.(2024·滨州)如图,在平面直角坐标系中,菱形的顶点轴上,边轴上,若点的坐标为(12,13),则点的坐标是 (0,-5) .
12.(2023·南充)如图所示,在菱形中,点分别在边上,,,分别与交于点.求证:
(1);
(2).
答案
13.如图所示,在中,平分∠,的垂直平分线分别交于点,连接.
(1)求证:四边形是菱形;
(2)若,求的长.
答案
13.(1)证明:∵CD平分∠ACB,
∴∠ACD=∠DCG.
∵EG垂直平分CD,
∴DG=CG,DE=EC.
∴∠DCG=∠GDC,∠ACD=∠EDC.
∴∠EDC=∠DCG=∠ACD=∠GDC.
∴CE//DG,DE//GC.
∴四边形DECG是平行四边形,且DE=EC.
∴四边形DGCE是菱形;
答案
14.在矩形中,两条对角线,相交于点,分别过点作,,且,连接.
(1)判断四边形的形状,并说明理由;
(2)若,,求四边形的面积.
答案
答案
答案
谢谢观看
2025年数学中考复习
5.25 菱形
基础知识
项目五 四边形
考点要求
壹
菱形
(1)理解掌握菱形的概念、性质及判定定理.
(2)会用菱形的有关知识进行证明,会计算菱形的面积.
核心知识点
贰
图形
菱形的性质
知识点1 菱形的性质
边 (1)四条边相等,即:AB===;
(2)对边平行;即:∥ ,∥
角 对角相等,即:=,=
对角线 (1)对角线互相垂直且平分,即:AC⊥BD,OA=
,OB=;
(2)对角线平分一组对角,即AC平分与
,BD平分 与
对称 性 菱形既是轴对称图形,又是中心对称图形,有两条对称轴.
(1)有一组 的平行四边形是菱形,即:在平行四边形 中, ,则四边形是菱形.
(2) 相等的四边形是菱形,即:四边形,则四边形是菱形.
(3)对角线 是菱形,即:在平行四边形 中,,则四边形是菱形.
知识点2 菱形的判定
邻边相等
四边
互相垂直的平行四边形
菱形的判定
知识点3 面积计算公式
利用平行四边形面积计算公式 S=底×高
利用对角线互桐垂直的性质计算 s=mn(m,n分别表示两条对角线的长)
考点攻坚
叁
考点1 菱形的性质
例1
(2023·丹东)如图所示,在菱形中,点分别是边的中点.
(1)求证:;
(2)若,,求菱形的面积.
考点2 菱形的面积
例2
(2023·邵阳)如图所示,在矩形中,,相交于点,,.
(1)求证:四边形是菱形;
(2)若,,求的长及四边形的面积.
专项训练
肆
达标训练
1.(2022·百色)如图所示,在菱形中,对角线相交于点,下列结论中错误是(C )
A. B. C. D.
2.(2024·大理)如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形的周长为
cm.
8
3.如图所示,在菱形中,点,分别是边,的中点,若,,则的长是 .
1
4.菱形是一种富有美感的图形,小吴收到一块矩形的玉石,想尽可能制作成较大面积的菱形模型,在设计图纸上取作为这个菱形的对角线.
(1)请你用尺规作图的方法把这个菱形画出来(保留作图痕迹,不用写作法);
(2)利用(1)中尺规作图过程中提供的条件证明你所作的图形是菱形.
答案
5.(2022,南京)如图所示,在平行四边形中,点分别在上,且,连接且相交于点.
(1)求证:四边形是平行四边形;
(2)若,求四边形的面积.
答案
6.如图,在中,,分别是,的中点.
(1)求证:≌.
(2)连接,当线段与满足什么条件时,四边形是菱形 并说明理由.
答案
6.(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB,CD=AB,
∵E、F分别是边AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF,
在△ADE和△CBF中,AD=CB,AE=CF,∠A=∠C
∴△ADE≌△CBF(SAS).
答案
课堂练习
伍
1.(2024·安庆)下列条件中,能判定四边形是菱形的是(D)
A.对角线垂直
B.两对角线相等
C.两对角线互相平分
D.两对角线互相垂直平分
2.(2024·东莞)如图,四边形为菱形,于点,则的长为(B )
A.4 B.4.8 C.5 D.6
3.(2022·张家界)如图所示,菱形的对角线相交于点,过点作于点,连接,,若菱形的面积为32,则的长为( )
A.4
B.4
C.8
D.8
C
4.(2021·贵阳)如图所示,是菱形的一条对角线,点的延长线上,若,则的度数为 64° .
5.(2024·广西)如图,两张宽度均为3cm的纸条交叉叠放在一起,交叉形成的锐角为60°,则重合部分构成的四边形的周长为 cm.
8
6.(2024·泉州)如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为,则 25 .
7.(2022.怀化)如图所示,四边形是菱形,,是对角线 上的两点,且,连接,,,.
求证:四边形是菱形.
答案
7.证明:连接,交于点.∵四边形是菱形,,,.又,,即,是平行四边形.又,即,四边形是菱形.
8.(2022·承德)如图所示,在中,对角线相交于点,.
(1)求证:;
(2)若点分别为的中点,连接,,求的长及四边形的周长.
答案
8.(1)证明:∵四边形是平行四边形,,∴四边形是菱形,∴.
(2)解:∵点分别为的中点,∴的中位线,∴.∵,∴.∵四边形是菱形,∴.∵,在Rt中,,,∴,∴菱形的周长为.
9.(2024·淄博).如图,在菱形中,,,动点,分别在线段上,且,则的最小值为 .
10.(2024·江西模拟)如图,菱形的周长为40,对角线相交于点,若点的中点,则的长是 .
11.(2024·滨州)如图,在平面直角坐标系中,菱形的顶点轴上,边轴上,若点的坐标为(12,13),则点的坐标是 (0,-5) .
12.(2023·南充)如图所示,在菱形中,点分别在边上,,,分别与交于点.求证:
(1);
(2).
答案
13.如图所示,在中,平分∠,的垂直平分线分别交于点,连接.
(1)求证:四边形是菱形;
(2)若,求的长.
答案
13.(1)证明:∵CD平分∠ACB,
∴∠ACD=∠DCG.
∵EG垂直平分CD,
∴DG=CG,DE=EC.
∴∠DCG=∠GDC,∠ACD=∠EDC.
∴∠EDC=∠DCG=∠ACD=∠GDC.
∴CE//DG,DE//GC.
∴四边形DECG是平行四边形,且DE=EC.
∴四边形DGCE是菱形;
答案
14.在矩形中,两条对角线,相交于点,分别过点作,,且,连接.
(1)判断四边形的形状,并说明理由;
(2)若,,求四边形的面积.
答案
答案
答案
谢谢观看
同课章节目录
