方程的根与函数的零点
图片预览





文档简介
课件19张PPT。方程的根与函数的零点思考:【学习目标】1.结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程的根的联系.
2.理解并会用函数在某个区间上存在零点的判定方法. 首先来观察几个具体的一元二次方程及其相应的二次函数方程 与函数
方程 与函数
方程 与函数
大家先自己解方程,然后大致画出函数图像
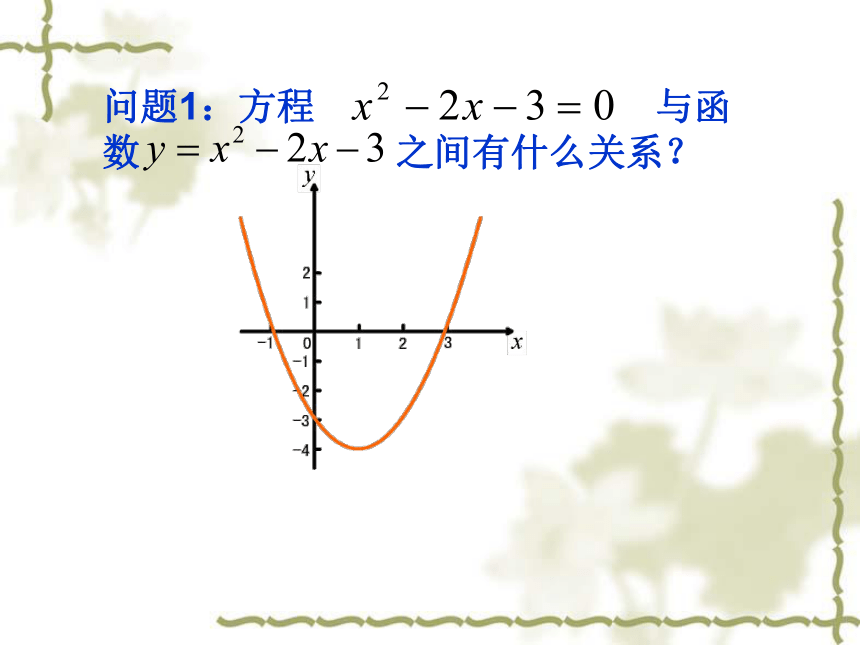
问题1:方程 与函 数 之间有什么关系? 方程ax2 +bx+c=0
(a>0)的根函数y= ax2 +bx
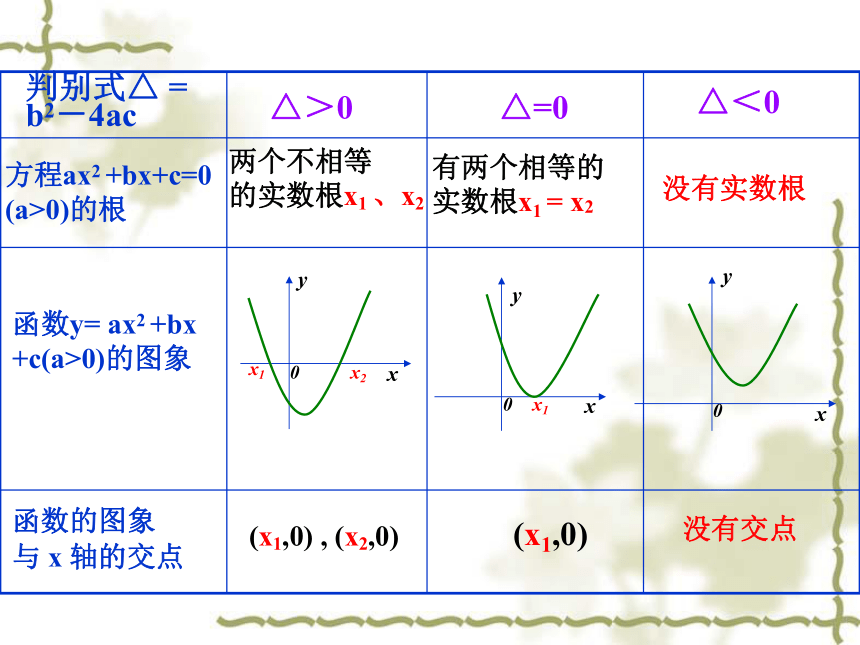
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。注意:零点指的是一个实数函数y=f(x)有零点方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点.例1:求函数f(x)=lg(x-1)的零点 (2)观察函数的图象
①在区间(a,b)上______(有/无)零点;f(a).f(b)_____0(<或>).
② 在区间(b,c)上______(有/无)零点;f(b).f(c) _____ 0(<或>).
③ 在区间(c,d)上______(有/无)零点;f(c).f(d) _____ 0(<或>).由以上探索,你可以得出什么样的结论? (3)若函数在某区间内存在零点,则函数在该区间上的图象是 (间断/连续);含零点的某一较小区间中以零点左右两边的实数为自变量,它们各自所对应的函数值的符号是 (相同/互异)结论思考:若函数y=f(x) 在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗? ③ ② ①④如果函数 y=f(x) 在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异即f(a)f(b)﹤0,且是单调函数那么,这个函数在(a,b)内必有惟一的一个零点。由表3-1和图3.1—3可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。解:用计算器或计算机作出x、f(x)的对应值表(表3-1)
和图象(图3.1—3)-4 -1.30691.09863.38635.60947.79189.945912.079414.1972例题 2 求函数f(x)=lnx+2x-6的零点个数。练习:求下列函数的零点:
(1)
(2)
(3)感悟收获,巩固拓展1、总结反思我掌握了哪些数学方法? 我还有哪些问题是感到困惑的? 我学到了哪些数学知识?
2.理解并会用函数在某个区间上存在零点的判定方法. 首先来观察几个具体的一元二次方程及其相应的二次函数方程 与函数
方程 与函数
方程 与函数
大家先自己解方程,然后大致画出函数图像
问题1:方程 与函 数 之间有什么关系? 方程ax2 +bx+c=0
(a>0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。注意:零点指的是一个实数函数y=f(x)有零点方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点.例1:求函数f(x)=lg(x-1)的零点 (2)观察函数的图象
①在区间(a,b)上______(有/无)零点;f(a).f(b)_____0(<或>).
② 在区间(b,c)上______(有/无)零点;f(b).f(c) _____ 0(<或>).
③ 在区间(c,d)上______(有/无)零点;f(c).f(d) _____ 0(<或>).由以上探索,你可以得出什么样的结论? (3)若函数在某区间内存在零点,则函数在该区间上的图象是 (间断/连续);含零点的某一较小区间中以零点左右两边的实数为自变量,它们各自所对应的函数值的符号是 (相同/互异)结论思考:若函数y=f(x) 在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗? ③ ② ①④如果函数 y=f(x) 在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异即f(a)f(b)﹤0,且是单调函数那么,这个函数在(a,b)内必有惟一的一个零点。由表3-1和图3.1—3可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。解:用计算器或计算机作出x、f(x)的对应值表(表3-1)
和图象(图3.1—3)-4 -1.30691.09863.38635.60947.79189.945912.079414.1972例题 2 求函数f(x)=lnx+2x-6的零点个数。练习:求下列函数的零点:
(1)
(2)
(3)感悟收获,巩固拓展1、总结反思我掌握了哪些数学方法? 我还有哪些问题是感到困惑的? 我学到了哪些数学知识?
