2025年数学中考专题一轮复习课件:5.26 正方形(共57张PPT)
文档属性
| 名称 | 2025年数学中考专题一轮复习课件:5.26 正方形(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 11:09:48 | ||
图片预览










文档简介
(共57张PPT)
2025年数学中考复习
5.26 正方形
基础知识
项目五 四边形
考点要求
壹
正方形
(1)理解并掌握正方形的概念性质及判定定理;
(2)会用正方形的有关知识进行证明和计算;
(3)了解正方形与矩形、菱形平行四边形之间的关系.
核心知识点
贰
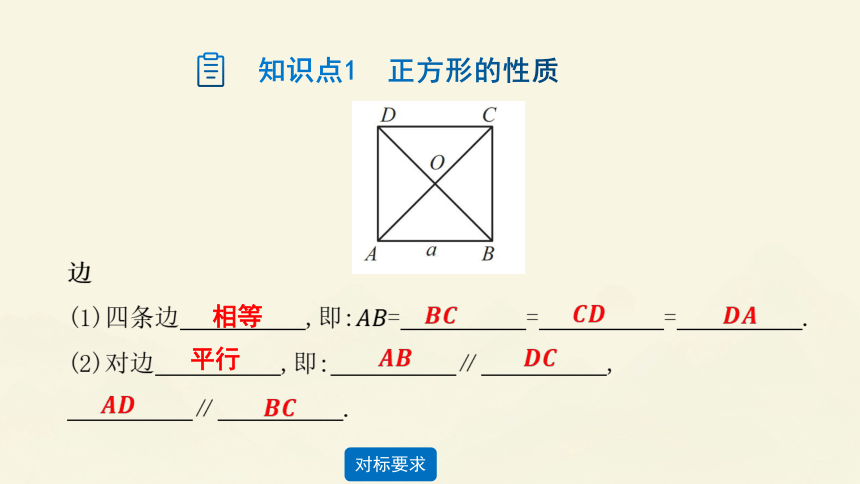
边
(1)四条边 ,即:= = = .
(2)对边 ,即: ∥ ,
∥ .
知识点1 正方形的性质
相等
平行
角
四个角都是 ,即:.
对角线
(1)对角线相等且互相 ,即:
(2)对角线平分一组对角;即平分 与 ,平分 与 .
对称性
正方形既是轴对称图形,又是中心对称图形,有 条对称轴.
直角
垂直平分
四
知识点2 正方形的判定
(1)有一组邻边相等,并且有一个角是 的平行四边形是正方形。即平行四边形是正方形;
(2)有一组 相等的矩形是正方形,即在矩形是正方形;
(3)对角线 的矩形是正方形,即在矩形是正方形;
直角
邻边
相互垂直
(4)有一个角是 的菱形是正方形,即菱形,则四边形是正方形;
(5)对角线相等的 是正方形,即,则四边形是正方形.
直角
菱形
知识点3 面积计算公式
利用平行四边形面积计算公式 S=a (a表示正方形的边长).
利用对角线互相垂直的性质计算 s=- m (m对角线的长).表示正方形
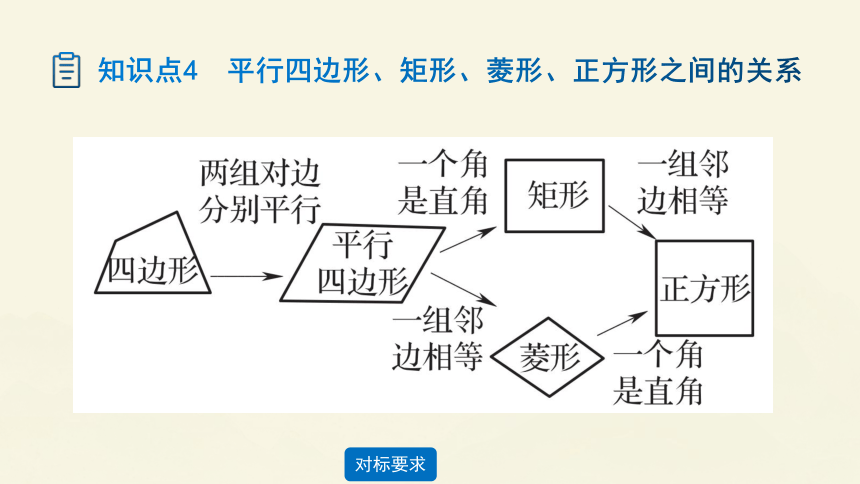
知识点4 平行四边形、矩形、菱形、正方形之间的关系
【温馨提示】
(1)平行四边形、矩形、菱形、正方形,都被任意一条过对角线交点的直线平分为面积相等的两个部分;
(2)矩形被它的两条对角线分为四个面积相等的等腰三角形;
(3)菱形被它的两条对角线分为四个全等的直角三角形.
知识点5 中点四边形
原图形 中点四边形 周长、面积
任意四边形 平行四边形 周长是原四边形对角线长度之和;面积是原四边形面积的一半。
矩形 菱形 菱形 矩形 正方形 正方形 对角线相等的四边形 菱形 对角线垂直的四边形 矩形 对角线垂直且相等的四边形 正方形 【温馨提示】
判断一个四边形的中点四边形形状的关键是判断其两条对角线的长度和位置关系.
考点攻坚
叁
考点1 正方形的性质
例1
(2023·广西)如图所示,在边长为2的正方形中,,分别是,上的动点,,分别是,的中点,则的最大值为 .
(2023·张家港)一个四边形顺次添加下列条件中的三个便得到正方形:
.两组对边分别相等 .一组对边平行且相等
.一组邻边相等 .一个角是直角
若顺次添加条件:①;②b→d→c;③.其中正确的是:( )
A.仅① B.仅③ C.①② D.②③
考点2 正方形的判定
例2
解析】:①由a得到两组对边分别相等的四边形是平行四边形,添加c,即一组邻边相等的平行四边形是菱形,再添加d,即一个角是直角的菱形是正方形,故①正确;②由b得到一组对边平行且相等的四边形是平行四边形,添加d,即有一个角是直角的平行四边形是矩形,再添加c,即一组邻边相等的矩形是正方形,故②正确;③由a得到两组对边分别相等的四边形是平行四边形,添加b,得到一组对边平行且相等的平行四边形仍是平行四边形,再添加c,即一组邻边相等的平行四边形是菱形,不能得到四边形是正方形,故③不正确。故选C
(2024·杭州)正方形工整、匀称、美观,设计方便,在人们的生活和生产实际中有着广泛的应用.图1为某园林石窗,其外框为边长为6的正方形(如图2),点分别为边上的中点,以四边形各边的三等分点的连线为边,分别向内作等边三角形(如),四个等边三角形的顶点恰好是正方形各边的中点,则点之间的距离是 .
考点3 中点四边形
例3
专项训练
肆
通关训练
1.(2022·绍兴)“方胜”是我国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图所示,将边长为2cm的正方形方向平移1cm得到正方形,形成一个“方胜”图案,则点之间的距离为(D)
A.1cm B.2cm C.(-1)cm D.(-1)cm
2.(2024·怀化)如图,在正方形中,分别是的中点,交于点,连接的延长线交的延长线于点,下列四个结论,其中正确的有( )
B
①DM AN;②∠ADM=∠P;③△COD为等边三角形;④DP=4AM
A.4 B.3 C.2 D.1
3.(2023·汉中)如图所示,在边长为2的正方形中,分别是边,的中点,连接,相交于点,是上的一点,且,则的长为 .
4.(2022· 大连)如图所示,正方形的边长是,将对角线绕点顺时针旋转的度数,点旋转后的对应点为的长是
(结果保留).
︵
提升训练
5.如图所示,在正方形内部作等边,交于点,过作,分别交于点,则的值是 .
6.(2023·湖南)问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形的边上任意取一点,以为边长向外作正方形,将正方形绕点顺时针旋转.
特例感知:
(1)当上时,连接,,小红发现点的中点,如图①.针对小红发现的结论,请给出证明.
(2)小红继续连接,并延长与相交,发现交点恰好也是,如图②,根据小红发现的结论,请判断 的形状,并说明理由.
规律探究:
(3)如图③所示,将正方形绕点顺时针旋转,连接,点是中点,连接,,,的形状是否发生改变 请说明理由.
答案
答案
答案
答案
课堂练习
伍
1.(2022·宁波)如图所示,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A.45° B.60°
C.67.5° D.77.5°
C
2.(2023·南昌)如图所示,正方形中,,将△沿对折至△,延长于点,刚好是边的中点,则的长是( B)
A.3 B.4 C.4.5 D.5
3.(2024·百色)如图,在菱形中,对角线相交于点,添加下列条件,能使菱形成为正方形的是( A )
A.AC=BD B.AC BD C.AD=AB D.AC平分∠DAB
4.(2024·聊城)如图,边长为4的正方形是圆的内接四边形,则阴影部分面积是.
5.(2023·黄山)如图所示,点是正方形的对角线上的一点,于点,,则点到直线的距离为 3 .
6.(2024·赣州)如图,四边形是正方形,,是对角线上的两点,且.
(1)求证:四边形是菱形;
(2)若,,求四边形的周长.
答案
答案
7.(2023·随州)如图所示,在平行四边形中,点分别在边上,且四边形为正方形.
(1)求证;
(2)已知平行四边形的面积为20,,求的长.
答案
8.(2024·昆明)如图,已知菱形,点是对角线所在直线上的两点,且,,连接,得四边形.
(1)求证:四边形是正方形;
(2)若,求菱形的面积.
答案
9. 如图所示,将正方形绕着点顺时针旋转60°得到正方形,连接,交于点.下列结论错误的是( )
D
A.∠EDC=30° B.AF=BG
C.∠AHB=60°
D.HC=FC
10.(2024·广西)如图,边长为5的正方形,分别为各边中点.连接,交点分别为,那么四边形的面积为( )
A.1 B.2 C.5 D.10
C
11.数学文化(2024·南通)
【阅读理解】明朝数学家程大位在数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”.
问题:
为了解决这个问题,需要依据问题建立数学模型.小明同学编写出了下列数学问题:
如图,秋千绳索静止的时候,踏板离地高一尺(1尺),将它往前推进两步(10尺),此时踏板升高离地五尺(5尺).已知:于点,于点,于点,.求:秋千绳索()的长度.请你解答下列问题:(1)四边形是 ;
A.一般平行四边形 B.矩形 C.菱形 D.正方形
(2)求的长.
B
答案
12.(2024·桂林)如图,在矩形中,的平分线交于点,于点,于点,交于点.
(1)求证:四边形是正方形;
(2)若,求证:;
(3)在(2)的条件下,已知,求的长.
答案
答案
谢谢观看
2025年数学中考复习
5.26 正方形
基础知识
项目五 四边形
考点要求
壹
正方形
(1)理解并掌握正方形的概念性质及判定定理;
(2)会用正方形的有关知识进行证明和计算;
(3)了解正方形与矩形、菱形平行四边形之间的关系.
核心知识点
贰
边
(1)四条边 ,即:= = = .
(2)对边 ,即: ∥ ,
∥ .
知识点1 正方形的性质
相等
平行
角
四个角都是 ,即:.
对角线
(1)对角线相等且互相 ,即:
(2)对角线平分一组对角;即平分 与 ,平分 与 .
对称性
正方形既是轴对称图形,又是中心对称图形,有 条对称轴.
直角
垂直平分
四
知识点2 正方形的判定
(1)有一组邻边相等,并且有一个角是 的平行四边形是正方形。即平行四边形是正方形;
(2)有一组 相等的矩形是正方形,即在矩形是正方形;
(3)对角线 的矩形是正方形,即在矩形是正方形;
直角
邻边
相互垂直
(4)有一个角是 的菱形是正方形,即菱形,则四边形是正方形;
(5)对角线相等的 是正方形,即,则四边形是正方形.
直角
菱形
知识点3 面积计算公式
利用平行四边形面积计算公式 S=a (a表示正方形的边长).
利用对角线互相垂直的性质计算 s=- m (m对角线的长).表示正方形
知识点4 平行四边形、矩形、菱形、正方形之间的关系
【温馨提示】
(1)平行四边形、矩形、菱形、正方形,都被任意一条过对角线交点的直线平分为面积相等的两个部分;
(2)矩形被它的两条对角线分为四个面积相等的等腰三角形;
(3)菱形被它的两条对角线分为四个全等的直角三角形.
知识点5 中点四边形
原图形 中点四边形 周长、面积
任意四边形 平行四边形 周长是原四边形对角线长度之和;面积是原四边形面积的一半。
矩形 菱形 菱形 矩形 正方形 正方形 对角线相等的四边形 菱形 对角线垂直的四边形 矩形 对角线垂直且相等的四边形 正方形 【温馨提示】
判断一个四边形的中点四边形形状的关键是判断其两条对角线的长度和位置关系.
考点攻坚
叁
考点1 正方形的性质
例1
(2023·广西)如图所示,在边长为2的正方形中,,分别是,上的动点,,分别是,的中点,则的最大值为 .
(2023·张家港)一个四边形顺次添加下列条件中的三个便得到正方形:
.两组对边分别相等 .一组对边平行且相等
.一组邻边相等 .一个角是直角
若顺次添加条件:①;②b→d→c;③.其中正确的是:( )
A.仅① B.仅③ C.①② D.②③
考点2 正方形的判定
例2
解析】:①由a得到两组对边分别相等的四边形是平行四边形,添加c,即一组邻边相等的平行四边形是菱形,再添加d,即一个角是直角的菱形是正方形,故①正确;②由b得到一组对边平行且相等的四边形是平行四边形,添加d,即有一个角是直角的平行四边形是矩形,再添加c,即一组邻边相等的矩形是正方形,故②正确;③由a得到两组对边分别相等的四边形是平行四边形,添加b,得到一组对边平行且相等的平行四边形仍是平行四边形,再添加c,即一组邻边相等的平行四边形是菱形,不能得到四边形是正方形,故③不正确。故选C
(2024·杭州)正方形工整、匀称、美观,设计方便,在人们的生活和生产实际中有着广泛的应用.图1为某园林石窗,其外框为边长为6的正方形(如图2),点分别为边上的中点,以四边形各边的三等分点的连线为边,分别向内作等边三角形(如),四个等边三角形的顶点恰好是正方形各边的中点,则点之间的距离是 .
考点3 中点四边形
例3
专项训练
肆
通关训练
1.(2022·绍兴)“方胜”是我国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图所示,将边长为2cm的正方形方向平移1cm得到正方形,形成一个“方胜”图案,则点之间的距离为(D)
A.1cm B.2cm C.(-1)cm D.(-1)cm
2.(2024·怀化)如图,在正方形中,分别是的中点,交于点,连接的延长线交的延长线于点,下列四个结论,其中正确的有( )
B
①DM AN;②∠ADM=∠P;③△COD为等边三角形;④DP=4AM
A.4 B.3 C.2 D.1
3.(2023·汉中)如图所示,在边长为2的正方形中,分别是边,的中点,连接,相交于点,是上的一点,且,则的长为 .
4.(2022· 大连)如图所示,正方形的边长是,将对角线绕点顺时针旋转的度数,点旋转后的对应点为的长是
(结果保留).
︵
提升训练
5.如图所示,在正方形内部作等边,交于点,过作,分别交于点,则的值是 .
6.(2023·湖南)问题情境:小红同学在学习了正方形的知识后,进一步进行以下探究活动:在正方形的边上任意取一点,以为边长向外作正方形,将正方形绕点顺时针旋转.
特例感知:
(1)当上时,连接,,小红发现点的中点,如图①.针对小红发现的结论,请给出证明.
(2)小红继续连接,并延长与相交,发现交点恰好也是,如图②,根据小红发现的结论,请判断 的形状,并说明理由.
规律探究:
(3)如图③所示,将正方形绕点顺时针旋转,连接,点是中点,连接,,,的形状是否发生改变 请说明理由.
答案
答案
答案
答案
课堂练习
伍
1.(2022·宁波)如图所示,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A.45° B.60°
C.67.5° D.77.5°
C
2.(2023·南昌)如图所示,正方形中,,将△沿对折至△,延长于点,刚好是边的中点,则的长是( B)
A.3 B.4 C.4.5 D.5
3.(2024·百色)如图,在菱形中,对角线相交于点,添加下列条件,能使菱形成为正方形的是( A )
A.AC=BD B.AC BD C.AD=AB D.AC平分∠DAB
4.(2024·聊城)如图,边长为4的正方形是圆的内接四边形,则阴影部分面积是.
5.(2023·黄山)如图所示,点是正方形的对角线上的一点,于点,,则点到直线的距离为 3 .
6.(2024·赣州)如图,四边形是正方形,,是对角线上的两点,且.
(1)求证:四边形是菱形;
(2)若,,求四边形的周长.
答案
答案
7.(2023·随州)如图所示,在平行四边形中,点分别在边上,且四边形为正方形.
(1)求证;
(2)已知平行四边形的面积为20,,求的长.
答案
8.(2024·昆明)如图,已知菱形,点是对角线所在直线上的两点,且,,连接,得四边形.
(1)求证:四边形是正方形;
(2)若,求菱形的面积.
答案
9. 如图所示,将正方形绕着点顺时针旋转60°得到正方形,连接,交于点.下列结论错误的是( )
D
A.∠EDC=30° B.AF=BG
C.∠AHB=60°
D.HC=FC
10.(2024·广西)如图,边长为5的正方形,分别为各边中点.连接,交点分别为,那么四边形的面积为( )
A.1 B.2 C.5 D.10
C
11.数学文化(2024·南通)
【阅读理解】明朝数学家程大位在数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”.
问题:
为了解决这个问题,需要依据问题建立数学模型.小明同学编写出了下列数学问题:
如图,秋千绳索静止的时候,踏板离地高一尺(1尺),将它往前推进两步(10尺),此时踏板升高离地五尺(5尺).已知:于点,于点,于点,.求:秋千绳索()的长度.请你解答下列问题:(1)四边形是 ;
A.一般平行四边形 B.矩形 C.菱形 D.正方形
(2)求的长.
B
答案
12.(2024·桂林)如图,在矩形中,的平分线交于点,于点,于点,交于点.
(1)求证:四边形是正方形;
(2)若,求证:;
(3)在(2)的条件下,已知,求的长.
答案
答案
谢谢观看
同课章节目录
