2024-2025学年人教版八年级下册数学第17章勾股定理基础解答题(含解析)
文档属性
| 名称 | 2024-2025学年人教版八年级下册数学第17章勾股定理基础解答题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 10:04:21 | ||
图片预览

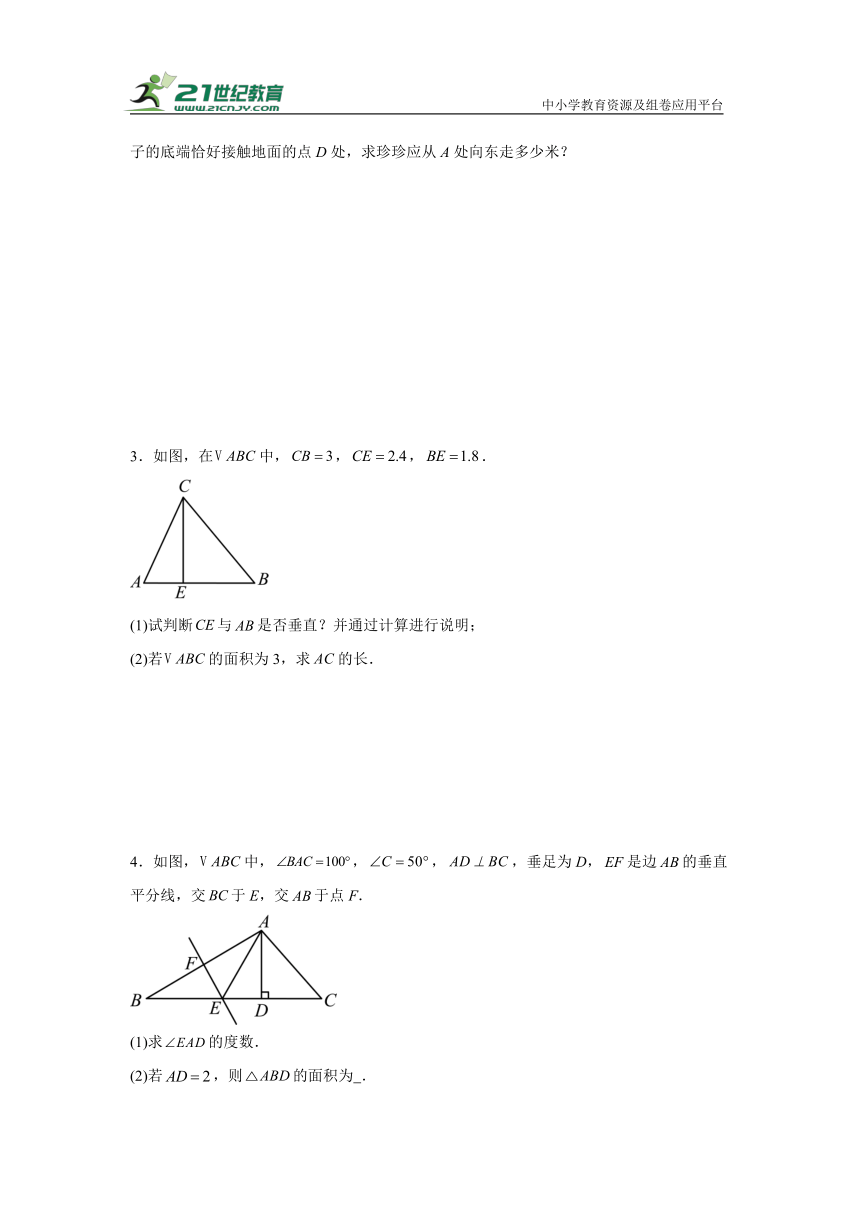

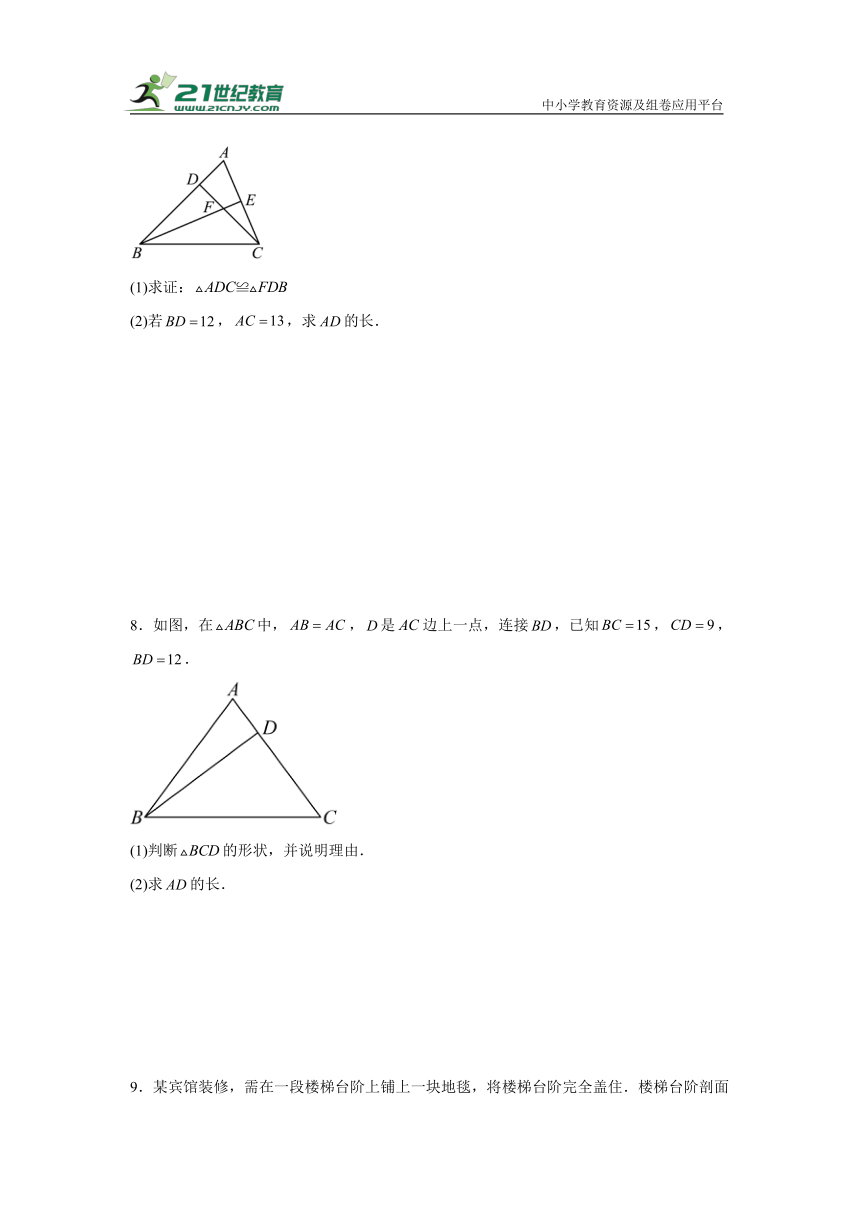
文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年人教版八年级下册数学第17章 勾股定理基础解答题
1.某宾馆装修,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图所示,已知,,.
(1)求的长;
(2)若已知楼梯宽,需要购买多少的地毯才能铺满所有台阶.
2.数学兴趣小组发现,系在旗杆顶端的绳子垂到地面时多出了3米,把绳子向外拉直,绳子的底端恰好接触地面的点A处(如图12所示),测得绳子底端A与旗杆根部C之间的距离为9米,设旗杆的高度为x米.
(1)用含x的式子表示绳子的长为________米;
(2)求旗杆的高度;
(3)珍珍在绳子底端又接上了长5米的绳子(接头处忽略不计),把绳子拉直,若要拼接后绳子的底端恰好接触地面的点D处,求珍珍应从A处向东走多少米?
3.如图,在中,,,.
(1)试判断与是否垂直?并通过计算进行说明;
(2)若的面积为3,求的长.
4.如图,中,,,,垂足为D,是边的垂直平分线,交于E,交于点F.
(1)求的度数.
(2)若,则的面积为 .
5.如图,在中,于点,,,.
(1)求的长;
(2)求的度数.
6.已知在中,,,,为边上的高.动点P从点A出发,沿着的三条边逆时针走一圈回到A点,速度为,设运动时间为t.
(1)求的长;
(2)当为等腰三角形时,求t的值.
7.已知:如图,在中,,,,与相交于点
(1)求证:
(2)若,,求的长.
8.如图,在中,,是边上一点,连接,已知,,.
(1)判断的形状,并说明理由.
(2)求的长.
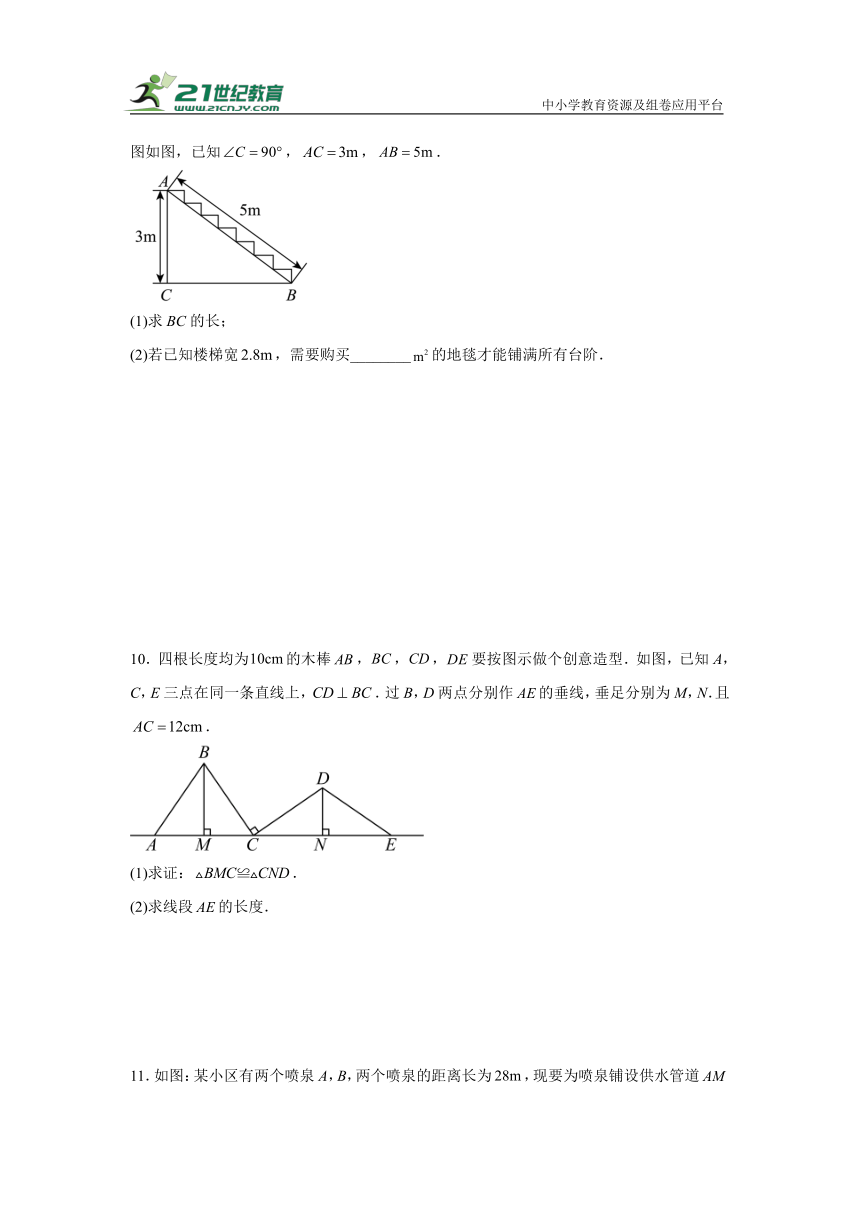
9.某宾馆装修,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图,已知,,.
(1)求BC的长;
(2)若已知楼梯宽,需要购买________的地毯才能铺满所有台阶.
10.四根长度均为的木棒,,,要按图示做个创意造型.如图,已知A,C,E三点在同一条直线上,.过B,D两点分别作的垂线,垂足分别为M,N.且.
(1)求证:.
(2)求线段的长度.
11.如图:某小区有两个喷泉A,B,两个喷泉的距离长为,现要为喷泉铺设供水管道和,供水点M在小路上,供水点 M 到的距离的长为,的长为.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)求喷泉B到小路的最短距离.
12.如图,为斜边上的高,的平分线分别交,于点E,F,,垂足为G.
(1)求证:.
(2)若厘米,厘米,求的长.
13.如图,在中,,点在上,,,垂足分别为、,且.
(1)求证:是的中点;
(2)若,,求的面积.
14.如图,,,,,.
(1)求的长度;
(2)线段与线段的位置关系是什么?请说明理由.
15.如图,在中,D是的中点,,垂足为D,交于点E,且.
(1)求证:是直角三角形;
(2)若,,求的长.
16.如图所示,与都是等腰直角三角形,,点为边上的一点.
(1)求证:;
(2)若,,求的长度.
17.如图,某社区有一块四边形空地,,,.从点修了一条垂直于的小路,垂足为.点恰好是的中点,且.
(1)求的长;
(2)连接,判断的形状并说明理由.
18.如图,在中,,,分别是腰,上的高.
(1)求证:;
(2)若,,求的长.
19.如图,在长方形中,,,为上的点,将沿折叠,使点落在长方形纳的点处.连接,已知.
(1)求证:为直角三角形;
(2)求线段的长.
20.如图,是的高线,为上一点,连结,交于点,.
(1)求证:是等腰三角形;
(2)若点是的中点,,,求的长.
21.如图,在中,,点P在上运动,点D在上,始终保持与相等,的垂直平分线交于点E,交于点F,连接.
(1)判断与的位置关系,并说明理由;
(2)若,,,求线段的长.
22.如图,长方形中,,,,把它沿折叠,使得点D与点B重合,点C落在点M的位置上.
(1)求证:;
(2)若,,求的面积;
(3)若,为等边三角形,直接写出的长.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025学年人教版八年级下册数学第17章 勾股定理基础解答题》参考答案
1.(1);
(2)需要购买的地毯才能铺满所有台阶.
【分析】此题考查了平移的性质,勾股定理的应用.
(1)根据勾股定理即可求解;
(2)根据题意,结合图形,把楼梯台阶的横竖分别向上向左平移,进一步求出面积即可.
【详解】(1)解:由题意可得,;
(2)解:利用平移可知,把楼梯台阶的横竖分别向上向左平移,地毯的长为,
∴地毯面积为,
答:需要购买的地毯才能铺满所有台阶.
2.(1)
(2)12米
(3)7
【分析】本题考查了勾股定理的应用,解题的关键是理解题意,学会构建方程解决问题.
(1)根据系在旗杆顶端的绳子垂到地面时多出了3米即可求解;
(2)根据勾股定理列方程求解即可;
(3)先根据勾股定理求出,即可得解.
【详解】(1)解:用含x的式子表示绳子的长为米,
故答案为:;
(2)解:由题意知:米,,
,
,
解得:,
旗杆的高度米;
(3)解:由(2)知,米,则米,
米,
米,
珍珍应从A处向东走7米.
3.(1),证明见解析
(2)
【分析】本题考查了勾股定理的性质和判定,解题的关键是熟练掌握勾股定理的性质和判定;
(1)根据勾股定理的判定,证明是直角三角形,即可得证;
(2)根据三角形的面积求出,再根据勾股定理的性质即可得解.
【详解】(1)解:,理由如下,
,
,
是直角三角形,且,
;
(2)解:,
,
,
.
4.(1)
(2)
【分析】(1)根据三角形内角和定理求出,根据线段垂直平分线的性质得到,进而得到根据三角形的外角性质、直角三角形的性质计算即可.
(2)先根据度所对的直角边是斜边的一半,得出,运用勾股定理列式计算,得,最后根据面积公式列式计算,即可作答.
【详解】(1)解:∵
∴,
∵是边的垂直平分线,
∴,
∴,
∴,
∵,
∴,
∴
(2)解:由(1)得,
∴在中,,
∴,
∴.
故答案为:.
【点睛】本题考查的是线段垂直平分线的性质、三角形内角和定理、三角形的外角性质,勾股定理,度所对的直角边是斜边的一半,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
5.(1)
(2)
【分析】本题考查勾股定理以及逆定理,掌握勾股定理以及逆定理是正确解答的前提
(1)根据勾股定理可求出答案;
(2)利用勾股定理求出,,再根据勾股定理的逆定理可得答案.
【详解】(1)解:(1),
,
在中,,,
;
(2)解:在中,,,
,
,
在中,
,,
,
.
6.(1)
(2)、8.4、9、9.5
【分析】本题考查的是等腰三角形的判定和性质、勾股定理的应用、掌握等腰三角形的判定定理和性质定理是解题的关键.
(1)根据勾股定理求出的长,根据三角形的面积公式计算;
(2)分点在上和在上两种情况,根据等腰三角形的判定定理计算.
【详解】(1)
解:中,,,,
,
,
,
解得,;
(2)
解:当点在上,时,,
则,
当点在上,时,
在中,,
如图1,,为边上的高,
,
则,
当时,,
当时,
如图2,作于,
则,,
由勾股定理得,,
则,
故当、8.4、9、9.5时,为等腰三角形;
7.(1)详见解析
(2)
【分析】本题考查全等三角形,三角形的内角和,等腰三角形的性质,勾股定理的应用,解题的关键是证明三角形全等.
(1)根据题意,可得,根据三角形的内角和,则,根据等角对等边,可得,最后根据全等三角形的判定方法求证,即可;
(2)由(1)得,推出,,根据勾股定理,可得,即可.
【详解】(1)解:证明如下:
∵,
∴
∴
∴
∵,
∴
∴
在和中,
,
∴.
(2)解:∵
∴,,
在中,,
∴,
∴.
8.(1)是直角三角形,理由见解答
(2)
【分析】本题考查了勾股定理,勾股定理的逆定理.
(1)根据勾股定理的逆定理可证是直角三角形,从而可得,然后利用平角定义可得,即可解答;
(2)设,则,然后在中,利用勾股定理进行计算即可.
【详解】(1)解:是直角三角形,
理由:在中,.,,
,,
,
是直角三角形,
,
,
是直角三角形;
(2)解:设,则,
,
,
在中,,
,
,
即.
9.(1);
(2).
【分析】此题考查了平移的性质,勾股定理的应用.
(1)根据勾股定理即可求解;
(2)根据题意,结合图形,把楼梯台阶的横竖分别向上向左平移,进一步求出面积即可.
【详解】(1)解:由题意可得,;
(2)解:利用平移可知,把楼梯台阶的横竖分别向上向左平移,地毯的长为,
∴地毯面积为,
故答案为:
10.(1)见解析
(2)
【分析】此题考查了全等三角形的判定与性质、勾股定理.
(1)结合垂直的定义、直角三角形的性质、平角的定义求出,,利用证明;
(2)根据等腰三角形的性质求出,,根据全等三角形的性质求出,再结合勾股定理求解即可.
【详解】(1)证明:∵,,
∴,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴;
(2)解:∵,,,,
∴,,
∵,
∴,
∴,
∴.
11.(1)供水点M到喷泉A,B需要铺设的管道总长为
(2)喷泉B到小路的最短距离为
【分析】此题考查了勾股定理的应用,解题的关键是掌握勾股定理.
(1)首先根据勾股定理求出,进而求解即可;
(2)过点B作,利用等面积法求解即可.
【详解】(1)∵在中,,,
∴
在中,
∴,
答:供水点M到喷泉A,B需要铺设的管道总长为;
(2)如图所示,过点B作,
.
答:喷泉B到小路的最短距离为.
12.(1)见解析
(2)8厘米
【分析】本题考查了角平分线的性质定理、等腰三角形的判定与性质、勾股定理,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由垂线的定义可得,从而得出,,由角平分线的定义可得,即可得证;
(2)结合对顶角相等可得,由等角对等边可得厘米,由角平分线的性质定理可得厘米,再由勾股定理可得厘米,即可得解.
【详解】(1)证明:由题意得:,,
∴,
∴,,
∵平分,
∴,
∴;
(2)解:∵,
∴,
∴厘米,
∵平分,,,
∴厘米,
∵,
∴,
∴,
∴厘米,
∴厘米.
13.(1)证明见解析
(2)
【分析】本题主要考查了角平分线的判定,等腰三角形的性质,直角三角形的性质,三角形面积的计算,解题的关键是熟练掌握等腰三角形“三线合一”.
(1)先根据角平分线的判定得出是的角平分线,然后根据等腰三角形的性质即可得出答案;
(2)先根据等腰三角形的性质得出,根据直角三角形的性质得出,根据勾股定理求出,根据三角形面积公式求出结果即可.
【详解】(1)证明:因为,,且,
所以是的角平分线,
因为在中,,
所以是的中点.
(2)解:因为是的中点,,
所以,
因为,,
所以,
,
所以,
答:的面积为.
14.(1)
(2);理由见解析
【分析】本题主要考查了勾股定理和逆定理,解题的关键是熟练掌握勾股定理,在一个直角三角形中,两条直角边分别为a、b,斜边为c,那么.如果一个三角形的三条边a、b、c满足,那么这个三角形为直角三角形.
(1)在中,直接利用勾股定理即可求出的长;
(2)利用勾股定理的逆定理判断出为直角三角形,其中,即可得证.
【详解】(1)解:∵,
∴,
∵,,
∴;
(2)解:;理由如下:
∵,,
∴,
∴为直角三角形,
∴,
∴.
15.(1)见解析
(2)
【分析】(1)先证,然后由可得,然后根据勾股定理逆定理即可证明结论;
(2)先用勾股定理求得,由(1)可得,再由勾股定理可得,最后联立求得即可.
【详解】(1)证明:∵D是的中点,,
∴
∵,
∴,即,
∴是直角三角形.
(2)解:∵,
∴,
在中,,,
∴,
∴,
由(1)可知为直角三角形,,
∴.
∵D是的中点,
∴,
在中,,由勾股定理得,
∴,
解得:.
【点睛】本题主要考查了勾股定理、勾股定理逆定理、线段垂直平分线的性质,熟练掌握勾股定理和逆定理,是解答本题的关键.
16.(1)证明见解析
(2)
【分析】(1)由与都是等腰直角三角形可得,,,由等边对等角及三角形的内角和定理可得,进而可得,然后利用即可得出结论;
(2)由(1)可得,,由全等三角形的性质可得,,进而可得,在中,由勾股定理可得,然后根据即可求出的长度.
【详解】(1)证明:与都是等腰直角三角形,
,,,
,
,
,
在和中,
,
;
(2)解:由(1)可得:,,
,,
,
在中,由勾股定理可得:
,
.
【点睛】本题主要考查了全等三角形的判定与性质,勾股定理,等边对等角,三角形的内角和定理,线段的和与差等知识点,利用证明及求出是解题的关键.
17.(1)
(2)是直角三角形
【分析】本题考查了勾股定理及其逆定理,垂直平分线的性质,掌握勾股定理和垂直平分线的性质是解题关键.
(1)利用勾股定理以及线段中点的性质即可.
(2)通过计算三条边的长度,根据勾股定理的逆定理来判断三角形的形状.
【详解】(1)解:,
.
在中,
,,
.
是的中点,
.
(2)解:如图,
,是的中点,
.
,,
,
,
是直角三角形.
18.(1)见解析
(2)6
【分析】本题考查的是全等三角形的判定与性质,勾股定理的应用;
(1)先证明,结合,,证明即可;
(2)由,,可得,结合全等三角形的性质可得答案.
【详解】(1)证明:∵,分别是腰,上的高,
∴
又∵,,
∴;
(2)解:∵,,,
∴
又由(1)得,,
∴.
19.(1)见解析;
(2)2.
【分析】本题考查了折叠的性质,勾股定理以及勾股逆定理,正确掌握相关性质内容是解题的关键.
(1)先由折叠得,结合故,即可作答.
(2)由折叠,可知.得证三点共线.再,则,结合勾股定理列式,再代入数值计算,即可作答.
【详解】(1)证明:由折叠,可知.
∵且,
∴.
根据勾股定理的逆定理,是直角三角形.
(2)解:由折叠,可知.
∵,
∴,
∴三点共线.
设,则,
∵,
∴.
在中,由勾股定理,得,
即.
解得.
即线段的长为2.
20.(1)见解析
(2)
【分析】(1)先根据等腰三角形的性质得到,再根据三角形的内角和定理证得,,进而可得,最后依据等腰三角形的判定,即可得证;
(2)过点作于点,根据点是的中点,可得,在中,根据勾股定理可得,进而证得,最后根据是等腰三角形,,即可求的长.
【详解】(1)证明:,
,
是的高线,
,
,,
,
,
,
是等腰三角形.
(2)解:过点作于点,
,
点是的中点,,
,
,,
,
,,,
,
,
是等腰三角形,,
.
【点睛】本题考查等腰三角形的判定与性质、全等三角形的判定与性质、三角形的内角和定理、勾股定理、对顶角的性质,掌握等腰三角形的判定与性质是解题的关键.
21.(1),见解析
(2)
【分析】(1)由题意知,,则,由是的垂直平分线,可得,由,可得,则,然后作答即可;
(2)如图,连接,设,则,由,可得,,由勾股定理得,,,则,计算求解即可.
【详解】(1)解:,理由如下;
由题意知,,
∴,
∵是的垂直平分线,
∴,
∵,
∴,
∴,
∴;
(2)解:如图,连接,
设,则,
∵,
∴,,
由勾股定理得,,,
∴,
解得,,
∴线段的长为.
【点睛】本题考查了等边对等角,垂直平分线的性质,三角形内角和定理,勾股定理等知识.熟练掌握等边对等角,垂直平分线的性质,三角形内角和定理,勾股定理是解题的关键.
22.(1)见解析
(2)
(3)
【分析】本题考查全等三角形的判定与性质,勾股定理,等边三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键,
(1)根据折叠的性质可得,,易证得;
(2)设,则,由勾股定理可推出,再根据全等的性质可得,即可求得的面积;
(3)根据折叠的性质可得,,根据为等边三角形,可得,由的直角三角形的性质可得,,在中,由勾股定理可得的长.
【详解】(1)证明:由折叠可知,,,,
∴,,
在和中,
∴,
(2)解:设,则,
在中,,
即,
解得:,即,
∴,
又∵,
∴,
∴,
(3)解:由折叠可知,,,
∵为等边三角形,
∴
∴,
设,则,
∵
∴,
解得:
∴,
在中,由勾股定理可得:,
∴.
中小学教育资源及组卷应用平台
2024-2025学年人教版八年级下册数学第17章 勾股定理基础解答题
1.某宾馆装修,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图所示,已知,,.
(1)求的长;
(2)若已知楼梯宽,需要购买多少的地毯才能铺满所有台阶.
2.数学兴趣小组发现,系在旗杆顶端的绳子垂到地面时多出了3米,把绳子向外拉直,绳子的底端恰好接触地面的点A处(如图12所示),测得绳子底端A与旗杆根部C之间的距离为9米,设旗杆的高度为x米.
(1)用含x的式子表示绳子的长为________米;
(2)求旗杆的高度;
(3)珍珍在绳子底端又接上了长5米的绳子(接头处忽略不计),把绳子拉直,若要拼接后绳子的底端恰好接触地面的点D处,求珍珍应从A处向东走多少米?
3.如图,在中,,,.
(1)试判断与是否垂直?并通过计算进行说明;
(2)若的面积为3,求的长.
4.如图,中,,,,垂足为D,是边的垂直平分线,交于E,交于点F.
(1)求的度数.
(2)若,则的面积为 .
5.如图,在中,于点,,,.
(1)求的长;
(2)求的度数.
6.已知在中,,,,为边上的高.动点P从点A出发,沿着的三条边逆时针走一圈回到A点,速度为,设运动时间为t.
(1)求的长;
(2)当为等腰三角形时,求t的值.
7.已知:如图,在中,,,,与相交于点
(1)求证:
(2)若,,求的长.
8.如图,在中,,是边上一点,连接,已知,,.
(1)判断的形状,并说明理由.
(2)求的长.
9.某宾馆装修,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图,已知,,.
(1)求BC的长;
(2)若已知楼梯宽,需要购买________的地毯才能铺满所有台阶.
10.四根长度均为的木棒,,,要按图示做个创意造型.如图,已知A,C,E三点在同一条直线上,.过B,D两点分别作的垂线,垂足分别为M,N.且.
(1)求证:.
(2)求线段的长度.
11.如图:某小区有两个喷泉A,B,两个喷泉的距离长为,现要为喷泉铺设供水管道和,供水点M在小路上,供水点 M 到的距离的长为,的长为.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)求喷泉B到小路的最短距离.
12.如图,为斜边上的高,的平分线分别交,于点E,F,,垂足为G.
(1)求证:.
(2)若厘米,厘米,求的长.
13.如图,在中,,点在上,,,垂足分别为、,且.
(1)求证:是的中点;
(2)若,,求的面积.
14.如图,,,,,.
(1)求的长度;
(2)线段与线段的位置关系是什么?请说明理由.
15.如图,在中,D是的中点,,垂足为D,交于点E,且.
(1)求证:是直角三角形;
(2)若,,求的长.
16.如图所示,与都是等腰直角三角形,,点为边上的一点.
(1)求证:;
(2)若,,求的长度.
17.如图,某社区有一块四边形空地,,,.从点修了一条垂直于的小路,垂足为.点恰好是的中点,且.
(1)求的长;
(2)连接,判断的形状并说明理由.
18.如图,在中,,,分别是腰,上的高.
(1)求证:;
(2)若,,求的长.
19.如图,在长方形中,,,为上的点,将沿折叠,使点落在长方形纳的点处.连接,已知.
(1)求证:为直角三角形;
(2)求线段的长.
20.如图,是的高线,为上一点,连结,交于点,.
(1)求证:是等腰三角形;
(2)若点是的中点,,,求的长.
21.如图,在中,,点P在上运动,点D在上,始终保持与相等,的垂直平分线交于点E,交于点F,连接.
(1)判断与的位置关系,并说明理由;
(2)若,,,求线段的长.
22.如图,长方形中,,,,把它沿折叠,使得点D与点B重合,点C落在点M的位置上.
(1)求证:;
(2)若,,求的面积;
(3)若,为等边三角形,直接写出的长.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025学年人教版八年级下册数学第17章 勾股定理基础解答题》参考答案
1.(1);
(2)需要购买的地毯才能铺满所有台阶.
【分析】此题考查了平移的性质,勾股定理的应用.
(1)根据勾股定理即可求解;
(2)根据题意,结合图形,把楼梯台阶的横竖分别向上向左平移,进一步求出面积即可.
【详解】(1)解:由题意可得,;
(2)解:利用平移可知,把楼梯台阶的横竖分别向上向左平移,地毯的长为,
∴地毯面积为,
答:需要购买的地毯才能铺满所有台阶.
2.(1)
(2)12米
(3)7
【分析】本题考查了勾股定理的应用,解题的关键是理解题意,学会构建方程解决问题.
(1)根据系在旗杆顶端的绳子垂到地面时多出了3米即可求解;
(2)根据勾股定理列方程求解即可;
(3)先根据勾股定理求出,即可得解.
【详解】(1)解:用含x的式子表示绳子的长为米,
故答案为:;
(2)解:由题意知:米,,
,
,
解得:,
旗杆的高度米;
(3)解:由(2)知,米,则米,
米,
米,
珍珍应从A处向东走7米.
3.(1),证明见解析
(2)
【分析】本题考查了勾股定理的性质和判定,解题的关键是熟练掌握勾股定理的性质和判定;
(1)根据勾股定理的判定,证明是直角三角形,即可得证;
(2)根据三角形的面积求出,再根据勾股定理的性质即可得解.
【详解】(1)解:,理由如下,
,
,
是直角三角形,且,
;
(2)解:,
,
,
.
4.(1)
(2)
【分析】(1)根据三角形内角和定理求出,根据线段垂直平分线的性质得到,进而得到根据三角形的外角性质、直角三角形的性质计算即可.
(2)先根据度所对的直角边是斜边的一半,得出,运用勾股定理列式计算,得,最后根据面积公式列式计算,即可作答.
【详解】(1)解:∵
∴,
∵是边的垂直平分线,
∴,
∴,
∴,
∵,
∴,
∴
(2)解:由(1)得,
∴在中,,
∴,
∴.
故答案为:.
【点睛】本题考查的是线段垂直平分线的性质、三角形内角和定理、三角形的外角性质,勾股定理,度所对的直角边是斜边的一半,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
5.(1)
(2)
【分析】本题考查勾股定理以及逆定理,掌握勾股定理以及逆定理是正确解答的前提
(1)根据勾股定理可求出答案;
(2)利用勾股定理求出,,再根据勾股定理的逆定理可得答案.
【详解】(1)解:(1),
,
在中,,,
;
(2)解:在中,,,
,
,
在中,
,,
,
.
6.(1)
(2)、8.4、9、9.5
【分析】本题考查的是等腰三角形的判定和性质、勾股定理的应用、掌握等腰三角形的判定定理和性质定理是解题的关键.
(1)根据勾股定理求出的长,根据三角形的面积公式计算;
(2)分点在上和在上两种情况,根据等腰三角形的判定定理计算.
【详解】(1)
解:中,,,,
,
,
,
解得,;
(2)
解:当点在上,时,,
则,
当点在上,时,
在中,,
如图1,,为边上的高,
,
则,
当时,,
当时,
如图2,作于,
则,,
由勾股定理得,,
则,
故当、8.4、9、9.5时,为等腰三角形;
7.(1)详见解析
(2)
【分析】本题考查全等三角形,三角形的内角和,等腰三角形的性质,勾股定理的应用,解题的关键是证明三角形全等.
(1)根据题意,可得,根据三角形的内角和,则,根据等角对等边,可得,最后根据全等三角形的判定方法求证,即可;
(2)由(1)得,推出,,根据勾股定理,可得,即可.
【详解】(1)解:证明如下:
∵,
∴
∴
∴
∵,
∴
∴
在和中,
,
∴.
(2)解:∵
∴,,
在中,,
∴,
∴.
8.(1)是直角三角形,理由见解答
(2)
【分析】本题考查了勾股定理,勾股定理的逆定理.
(1)根据勾股定理的逆定理可证是直角三角形,从而可得,然后利用平角定义可得,即可解答;
(2)设,则,然后在中,利用勾股定理进行计算即可.
【详解】(1)解:是直角三角形,
理由:在中,.,,
,,
,
是直角三角形,
,
,
是直角三角形;
(2)解:设,则,
,
,
在中,,
,
,
即.
9.(1);
(2).
【分析】此题考查了平移的性质,勾股定理的应用.
(1)根据勾股定理即可求解;
(2)根据题意,结合图形,把楼梯台阶的横竖分别向上向左平移,进一步求出面积即可.
【详解】(1)解:由题意可得,;
(2)解:利用平移可知,把楼梯台阶的横竖分别向上向左平移,地毯的长为,
∴地毯面积为,
故答案为:
10.(1)见解析
(2)
【分析】此题考查了全等三角形的判定与性质、勾股定理.
(1)结合垂直的定义、直角三角形的性质、平角的定义求出,,利用证明;
(2)根据等腰三角形的性质求出,,根据全等三角形的性质求出,再结合勾股定理求解即可.
【详解】(1)证明:∵,,
∴,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴;
(2)解:∵,,,,
∴,,
∵,
∴,
∴,
∴.
11.(1)供水点M到喷泉A,B需要铺设的管道总长为
(2)喷泉B到小路的最短距离为
【分析】此题考查了勾股定理的应用,解题的关键是掌握勾股定理.
(1)首先根据勾股定理求出,进而求解即可;
(2)过点B作,利用等面积法求解即可.
【详解】(1)∵在中,,,
∴
在中,
∴,
答:供水点M到喷泉A,B需要铺设的管道总长为;
(2)如图所示,过点B作,
.
答:喷泉B到小路的最短距离为.
12.(1)见解析
(2)8厘米
【分析】本题考查了角平分线的性质定理、等腰三角形的判定与性质、勾股定理,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由垂线的定义可得,从而得出,,由角平分线的定义可得,即可得证;
(2)结合对顶角相等可得,由等角对等边可得厘米,由角平分线的性质定理可得厘米,再由勾股定理可得厘米,即可得解.
【详解】(1)证明:由题意得:,,
∴,
∴,,
∵平分,
∴,
∴;
(2)解:∵,
∴,
∴厘米,
∵平分,,,
∴厘米,
∵,
∴,
∴,
∴厘米,
∴厘米.
13.(1)证明见解析
(2)
【分析】本题主要考查了角平分线的判定,等腰三角形的性质,直角三角形的性质,三角形面积的计算,解题的关键是熟练掌握等腰三角形“三线合一”.
(1)先根据角平分线的判定得出是的角平分线,然后根据等腰三角形的性质即可得出答案;
(2)先根据等腰三角形的性质得出,根据直角三角形的性质得出,根据勾股定理求出,根据三角形面积公式求出结果即可.
【详解】(1)证明:因为,,且,
所以是的角平分线,
因为在中,,
所以是的中点.
(2)解:因为是的中点,,
所以,
因为,,
所以,
,
所以,
答:的面积为.
14.(1)
(2);理由见解析
【分析】本题主要考查了勾股定理和逆定理,解题的关键是熟练掌握勾股定理,在一个直角三角形中,两条直角边分别为a、b,斜边为c,那么.如果一个三角形的三条边a、b、c满足,那么这个三角形为直角三角形.
(1)在中,直接利用勾股定理即可求出的长;
(2)利用勾股定理的逆定理判断出为直角三角形,其中,即可得证.
【详解】(1)解:∵,
∴,
∵,,
∴;
(2)解:;理由如下:
∵,,
∴,
∴为直角三角形,
∴,
∴.
15.(1)见解析
(2)
【分析】(1)先证,然后由可得,然后根据勾股定理逆定理即可证明结论;
(2)先用勾股定理求得,由(1)可得,再由勾股定理可得,最后联立求得即可.
【详解】(1)证明:∵D是的中点,,
∴
∵,
∴,即,
∴是直角三角形.
(2)解:∵,
∴,
在中,,,
∴,
∴,
由(1)可知为直角三角形,,
∴.
∵D是的中点,
∴,
在中,,由勾股定理得,
∴,
解得:.
【点睛】本题主要考查了勾股定理、勾股定理逆定理、线段垂直平分线的性质,熟练掌握勾股定理和逆定理,是解答本题的关键.
16.(1)证明见解析
(2)
【分析】(1)由与都是等腰直角三角形可得,,,由等边对等角及三角形的内角和定理可得,进而可得,然后利用即可得出结论;
(2)由(1)可得,,由全等三角形的性质可得,,进而可得,在中,由勾股定理可得,然后根据即可求出的长度.
【详解】(1)证明:与都是等腰直角三角形,
,,,
,
,
,
在和中,
,
;
(2)解:由(1)可得:,,
,,
,
在中,由勾股定理可得:
,
.
【点睛】本题主要考查了全等三角形的判定与性质,勾股定理,等边对等角,三角形的内角和定理,线段的和与差等知识点,利用证明及求出是解题的关键.
17.(1)
(2)是直角三角形
【分析】本题考查了勾股定理及其逆定理,垂直平分线的性质,掌握勾股定理和垂直平分线的性质是解题关键.
(1)利用勾股定理以及线段中点的性质即可.
(2)通过计算三条边的长度,根据勾股定理的逆定理来判断三角形的形状.
【详解】(1)解:,
.
在中,
,,
.
是的中点,
.
(2)解:如图,
,是的中点,
.
,,
,
,
是直角三角形.
18.(1)见解析
(2)6
【分析】本题考查的是全等三角形的判定与性质,勾股定理的应用;
(1)先证明,结合,,证明即可;
(2)由,,可得,结合全等三角形的性质可得答案.
【详解】(1)证明:∵,分别是腰,上的高,
∴
又∵,,
∴;
(2)解:∵,,,
∴
又由(1)得,,
∴.
19.(1)见解析;
(2)2.
【分析】本题考查了折叠的性质,勾股定理以及勾股逆定理,正确掌握相关性质内容是解题的关键.
(1)先由折叠得,结合故,即可作答.
(2)由折叠,可知.得证三点共线.再,则,结合勾股定理列式,再代入数值计算,即可作答.
【详解】(1)证明:由折叠,可知.
∵且,
∴.
根据勾股定理的逆定理,是直角三角形.
(2)解:由折叠,可知.
∵,
∴,
∴三点共线.
设,则,
∵,
∴.
在中,由勾股定理,得,
即.
解得.
即线段的长为2.
20.(1)见解析
(2)
【分析】(1)先根据等腰三角形的性质得到,再根据三角形的内角和定理证得,,进而可得,最后依据等腰三角形的判定,即可得证;
(2)过点作于点,根据点是的中点,可得,在中,根据勾股定理可得,进而证得,最后根据是等腰三角形,,即可求的长.
【详解】(1)证明:,
,
是的高线,
,
,,
,
,
,
是等腰三角形.
(2)解:过点作于点,
,
点是的中点,,
,
,,
,
,,,
,
,
是等腰三角形,,
.
【点睛】本题考查等腰三角形的判定与性质、全等三角形的判定与性质、三角形的内角和定理、勾股定理、对顶角的性质,掌握等腰三角形的判定与性质是解题的关键.
21.(1),见解析
(2)
【分析】(1)由题意知,,则,由是的垂直平分线,可得,由,可得,则,然后作答即可;
(2)如图,连接,设,则,由,可得,,由勾股定理得,,,则,计算求解即可.
【详解】(1)解:,理由如下;
由题意知,,
∴,
∵是的垂直平分线,
∴,
∵,
∴,
∴,
∴;
(2)解:如图,连接,
设,则,
∵,
∴,,
由勾股定理得,,,
∴,
解得,,
∴线段的长为.
【点睛】本题考查了等边对等角,垂直平分线的性质,三角形内角和定理,勾股定理等知识.熟练掌握等边对等角,垂直平分线的性质,三角形内角和定理,勾股定理是解题的关键.
22.(1)见解析
(2)
(3)
【分析】本题考查全等三角形的判定与性质,勾股定理,等边三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键,
(1)根据折叠的性质可得,,易证得;
(2)设,则,由勾股定理可推出,再根据全等的性质可得,即可求得的面积;
(3)根据折叠的性质可得,,根据为等边三角形,可得,由的直角三角形的性质可得,,在中,由勾股定理可得的长.
【详解】(1)证明:由折叠可知,,,,
∴,,
在和中,
∴,
(2)解:设,则,
在中,,
即,
解得:,即,
∴,
又∵,
∴,
∴,
(3)解:由折叠可知,,,
∵为等边三角形,
∴
∴,
设,则,
∵
∴,
解得:
∴,
在中,由勾股定理可得:,
∴.
