2025年浙江省中考数学一轮复习专题检测 专题16 三角形(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题16 三角形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 09:55:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题16 三角形
一.选择题
1.(2024 湖南三模)下列各组长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,1,2 C.1,2,2 D.1,5,7
2.(2024 拱墅区一模)王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
3.(2024 鄞州区模拟)如图,直线l1∥l2,以直线l2上的点A为圆心适当长为半径画弧,分别交直线l1、l2于点B、C,连结AB、BC.若∠ACB=68°,则∠1的度数为( )
A.22° B.32° C.44° D.68°
4.(2024 桥西区模拟)平面内,将长分别为1,1,3,x的线段,首尾顺次相接组成凸四边形(如图),x可能是( )
A.1 B.3 C.5 D.7
5.(2024 山西模拟)为了比较与的大小,小亮先画了一条数轴,然后在原点O处作了一条垂线段OA,且OA=1,点B表示的数是2,点C表示的数为3,连接AB,AC,由AB+BC>AC推出,这里小亮用到的数学思想是( )
A.统计思想 B.数形结合 C.模型思想 D.分类讨论
6.(2024 汉川市模拟)已知△ABC中,其中有两边长是2和5,且△ABC的第三边长是偶数,则此三角形的周长为( )
A.11 B.12 C.13 D.11或13
7.(2024 重庆模拟)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
8.(2024 瑶海区一模)如图,在△ABC中,∠B+∠C=110°,AM平分∠BAC,交BC于点M,MN∥AB,交AC于点N,则∠AMN的大小是( )
A.30° B.35° C.40° D.55°
9.(2024 肥东县模拟)如图,将一副三角板的直角顶点重合并部分重叠,若∠BOD=20°,则∠AEC的度数为( )
A.30° B.35° C.40° D.45°
10.(2024 榆阳区二模)将一副三角板和一个直尺按如图所示的位置摆放,直角边BC与直尺的一边重合,点E在AC上,∠ABC=∠D=90°,∠A=30°,∠DEC=45°,则∠1的度数为( )
A.75° B.70° C.65° D.60°
11.(2024 西宁)如图,在△ABC中,AD是角平分线,BE是中线,AD=BE,且AD⊥BE,垂足为F,G为DC的中点,连接DE,EG.下列结论错误的是( )
A.△AFB≌△AFE B.∠ADB=∠ADE C.FD=BE D.△CEG~△CBE
12.(2024 宁夏)如图,在Rt△ABC中,∠ABC=90°,AB=3cm,BC=2cm,点A在直线l1上,点B,C在直线l2上,l1∥l2,动点P从点A出发沿直线l1以1cm/s的速度向右运动,设运动时间为t s.
下列结论:
①当t=2s时,四边形ABCP的周长是10cm;
②当t=4s时,点P到直线l2的距离等于5cm;
③在点P运动过程中,△PBC的面积随着t的增大而增大;
④若点D,E分别是线段PB,PC的中点,在点P运动过程中,线段DE的长度不变.
其中正确的是( )
A.①④ B.②③ C.①③ D.②④
二.填空题
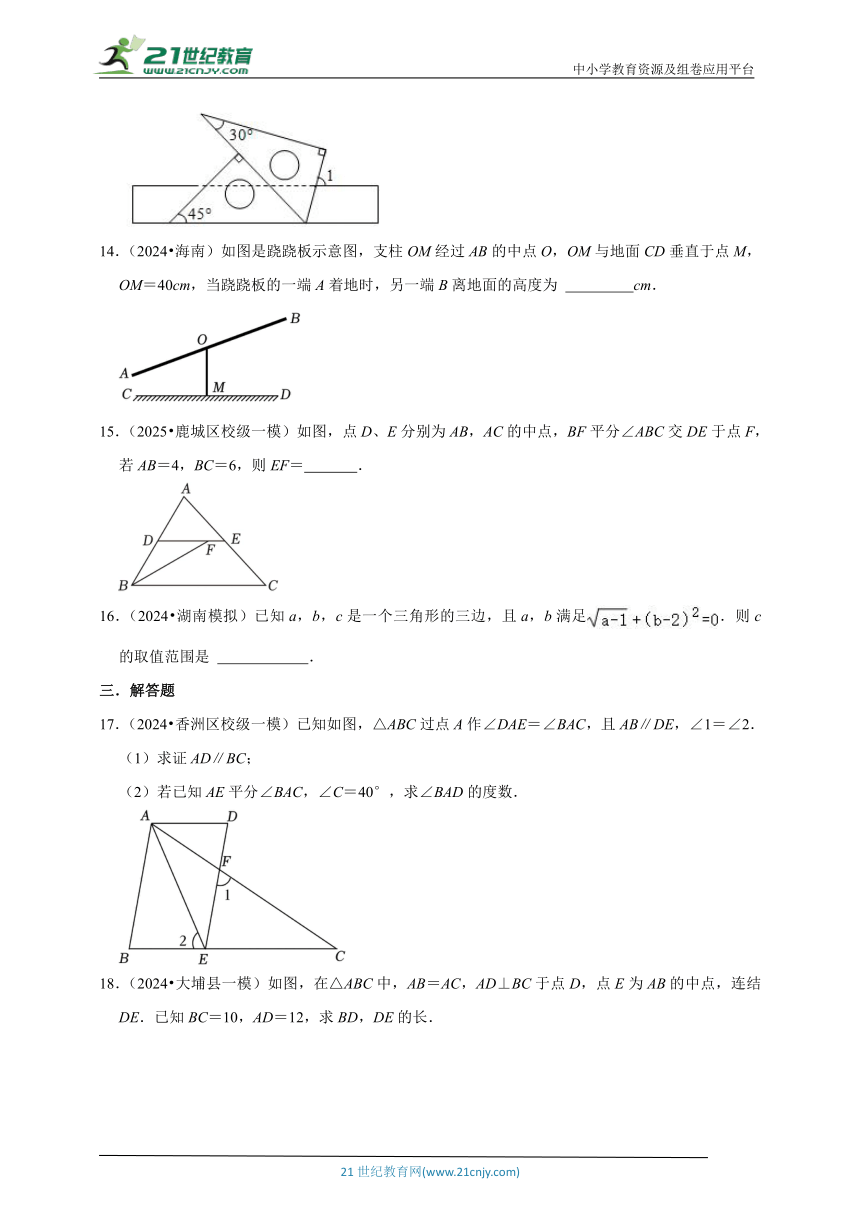
13.(2024 上饶一模)将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为 .
14.(2024 海南)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=40cm,当跷跷板的一端A着地时,另一端B离地面的高度为 cm.
15.(2025 鹿城区校级一模)如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= .
16.(2024 湖南模拟)已知a,b,c是一个三角形的三边,且a,b满足.则c的取值范围是 .
三.解答题
17.(2024 香洲区校级一模)已知如图,△ABC过点A作∠DAE=∠BAC,且AB∥DE,∠1=∠2.
(1)求证AD∥BC;
(2)若已知AE平分∠BAC,∠C=40°,求∠BAD的度数.
18.(2024 大埔县一模)如图,在△ABC中,AB=AC,AD⊥BC于点D,点E为AB的中点,连结DE.已知BC=10,AD=12,求BD,DE的长.
19.(2024 潍城区二模)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种
证明方法.
已知:如图甲, .
求证:∠A+∠B+∠C=180°.
证明:如图乙,作BC的延长线CD,在△ABC外部,以CA为一边,作∠ACE=∠A.
所以,CE∥AB(内错角相等,两直线平行).
所以,∠B=∠ECD( ).
因为,∠ACB,∠ACE,∠ECD组成一个平角,
所以,∠ACB+∠ACE+∠ECD=180°(平角的定义),
所以,∠ACB+∠A+∠B=180°( ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
20.(2024 青岛一模)【探究1】
如图1,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= °;
【探究2】
如图2,∠BAD的三等分线AE与∠BCD的三等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= °;
【探究3】
如图3,∠BAD的n等分线AE与∠BCD的n等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=x°,∠ADC=y°,则∠AEC= °(用含x,y,n的式子表示).
21.(2024 柯桥区模拟)问题提出:
(1)如图①,在△ABC中,点M,N分别是AB,AC的中点,若BC=6,则MN的长为 .
问题探究:
(2)如图②,在正方形ABCD中,AD=6,点E为AD上的靠近点A的三等分点,点F为AB上的动点,将△AEF折叠,点A的对应点G,求CG的最小值.
问题解决:
(3)如图③,某地要规划一个五边形艺术中心ABCDE,已知∠ABC=120°,∠BCD=60°,AB=AE=20m,BC=CD=40m,点C处为参观入口,DE的中点P处规划为“优秀”作品展台,求点C与点P之间的最小距离.
答案与解析
一.选择题
1.(2024 湖南三模)下列各组长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,1,2 C.1,2,2 D.1,5,7
【点拨】根据三角形的任意两边的和大于第三边,任意两边之差小于第三边,只要把三边代入,看是否满足即可.
【解析】解:A.1+2=3,不能构成三角形,不合题意;
B.1+1=2,不能构成三角形,不合题意;
C..1+2>2,能构成三角形,符合题意;
D.1+5<7,不能构成三角形,不合题意.
故选:C.
【点睛】此题主要考查了三角形的三边关系,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.
2.(2024 拱墅区一模)王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线 C.高线 D.以上都不是
【点拨】根据三角形的中线把三角形分为面积相等的两部分解答.
【解析】解:由三角形的面积公式可知,三角形的中线把三角形分为面积相等的两部分,
∴他所作的线段AD应该是△ABC的中线,
故选:B.
【点睛】本题考查的是三角形的面积计算,掌握三角形的中线把三角形分为面积相等的两部分是解题的关键.
3.(2024 鄞州区模拟)如图,直线l1∥l2,以直线l2上的点A为圆心适当长为半径画弧,分别交直线l1、l2于点B、C,连结AB、BC.若∠ACB=68°,则∠1的度数为( )
A.22° B.32° C.44° D.68°
【点拨】由题意可得AB=AC,则有∠ABC=∠ACB=68°,再利用三角形的内角和即可求∠1的度数.
【解析】解:∵以直线l2上的点A为圆心适当长为半径画弧,分别交直线l1、l2于点B、C,
∴AB=AC,
∴∠ABC=∠ACB=68°,
在△ABC中,∠1=180°﹣∠ABC﹣∠ACB=44°.
故选:C.
【点睛】本题主要考查三角形的内角和定理,等腰三角形的性质,解答的关键是由题意得到AB=AC.
4.(2024 桥西区模拟)平面内,将长分别为1,1,3,x的线段,首尾顺次相接组成凸四边形(如图),x可能是( )
A.1 B.3 C.5 D.7
【点拨】由三角形三边关系定理得到2<AC<4,AC﹣1<x<AC+1,因此1<x<5,即可得到答案.
【解析】解:连接AC,
在△ACD中,3﹣1<AC<3+1,
∴2<AC<4,
在△ABC中,AC﹣1<x<AC+1,
∴1<x<5,
∴x可能是3.
故选:B.
【点睛】本题考查三角形的三边关系,关键是连接AC,应用三角形的三边关系定理来解决问题.
5.(2024 山西模拟)为了比较与的大小,小亮先画了一条数轴,然后在原点O处作了一条垂线段OA,且OA=1,点B表示的数是2,点C表示的数为3,连接AB,AC,由AB+BC>AC推出,这里小亮用到的数学思想是( )
A.统计思想 B.数形结合 C.模型思想 D.分类讨论
【点拨】由数形结合思想,即可得到答案.
【解析】解:这里小亮用到的数学思想是数形结合.
故选:B.
【点睛】本题考查三角形三边关系,实数与数轴,实数大小比较,数学思想,关键是掌握数形结合思想.
6.(2024 汉川市模拟)已知△ABC中,其中有两边长是2和5,且△ABC的第三边长是偶数,则此三角形的周长为( )
A.11 B.12 C.13 D.11或13
【点拨】三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边,设第三边长x,得到3<x<7,由△ABC的第三边长是偶数,得到x=4或6,于是得到此三角形的周长.
【解析】解:设第三边长x,
∴5﹣2<x<5+2,
∴3<x<7,
∵△ABC的第三边长是偶数,
∴x=4或6,
∴此三角形的周长为2+5+4=11或2+5+6=13.
故选:D.
【点睛】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
7.(2024 重庆模拟)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90° C.∠BAF=∠CAF D.S△ABC=2S△ABF
【点拨】根据三角形的角平分线、中线和高的概念判断.
【解析】解:∵AF是△ABC的中线,
∴BF=CF,A说法正确,不符合题意;
∵AD是高,
∴∠ADC=90°,
∴∠C+∠CAD=90°,B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE,而∠BAF与∠CAF不一定相等,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF,D说法正确,不符合题意;
故选:C.
【点睛】本题考查的是三角形的角平分线、中线和高,掌握它们的概念是解题的关键.
8.(2024 瑶海区一模)如图,在△ABC中,∠B+∠C=110°,AM平分∠BAC,交BC于点M,MN∥AB,交AC于点N,则∠AMN的大小是( )
A.30° B.35° C.40° D.55°
【点拨】先根据已知条件和三角形的内角和为180°,求出∠BAC的度数,再根据已知条件和角平分线的定义,求出∠BAM,最后根据MN∥AB,求出∠AMN即可.
【解析】解:∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣(∠B+∠C)=180°﹣110°=70°,
∵AM平分∠BAC,
∴∠BAM=,
∵MN∥AB,
∴∠AMN=∠BAM=35°,
故选:B.
【点睛】本题主要考查了三角形内角和定理和平行线的性质,解题关键是熟练掌握三角形三个内角的和是180°和平行线的性质.
9.(2024 肥东县模拟)如图,将一副三角板的直角顶点重合并部分重叠,若∠BOD=20°,则∠AEC的度数为( )
A.30° B.35° C.40° D.45°
【点拨】根据三角形内角和定理求出∠B的度数,进而根据三角形外角的性质求出∠AFO的度数,再由三角形外角的性质求出∠DEF的度数,最后根据对顶角相等即可得到答案.
【解析】解:如图,
由题意得,∠B=180°﹣30°﹣90°=60°,
∵∠BOD=20°,
∴∠AFO=∠BOD+∠B=80°,
∴∠DEF=∠AFO﹣∠D=35°,
∴∠AEC=∠DEB=35°,
故选:B.
【点睛】本题主要考查了三角形内角和定理,三角形外角的性质,熟练掌握各知识点是解题的关键.
10.(2024 榆阳区二模)将一副三角板和一个直尺按如图所示的位置摆放,直角边BC与直尺的一边重合,点E在AC上,∠ABC=∠D=90°,∠A=30°,∠DEC=45°,则∠1的度数为( )
A.75° B.70° C.65° D.60°
【点拨】在图中标记∠2,利用三角形内角和定理,可求出∠ACB及∠DCE的度数,结合邻补角互补,可求出∠2的度数,由直尺的对边平行,再利用“两直线平行,同位角相等”,即可求出∠1的度数.
【解析】解:在图中标记∠2,如图所示.
∵∠ACB=180°﹣90°﹣30°=60°,∠DCE=180°﹣90°﹣45°=45°,
∴∠2=180°﹣∠ACB﹣∠DCE=180°﹣60°﹣45°=75°.
∵直尺的对边平行,
∴∠1=∠2=75°.
故选:A.
【点睛】本题考查了三角形内角和定理、平行线的性质以及余角和补角,利用三角形内角和定理及邻补角互补,找出∠2的度数是解题的关键.
11.(2024 西宁)如图,在△ABC中,AD是角平分线,BE是中线,AD=BE,且AD⊥BE,垂足为F,G为DC的中点,连接DE,EG.下列结论错误的是( )
A.△AFB≌△AFE B.∠ADB=∠ADE C.FD=BE D.△CEG~△CBE
【点拨】根据三角形全等可判断A,B两选项,根据三角形中位线性质,可判断C选项,以及相似三角形的判断,从而得到结果.
【解析】解:∵AD是角平分线,
∴∠BAD=∠EAD,
∵AD⊥BE,
∴∠AFB=∠AFE=90°,
又∵AF=AF,
∴△AFB≌△AFE(ASA),
故A选项正确,不符合题意;
∵△AFB≌△AFE,
∴AB=AE,
∵∠BAD=∠EAD,AD=AD,
∴△ADB≌△ADE(SAS),
∴∠ADB=∠ADE,
故B选项正确,不符合题意;
∵BE是中线,
∴CE=EA,
∵G为DC的中点,
∴CG=GD,
∴EG是△CAD中位线,
∴EG=AD,EG∥AD,
∴,
又∵△AFB≌△AFE,
∴BF=FE,
∴BD=GD,
∴DF是△BEG的中位线,
∴DF=EG,
∴DF=AD,
∵AD=BE,
∴DF=BE,
故C选项正确,不符合题意;
在△CEG和△CBE中,∠C为公共角,
但∠CEG和∠CBE,∠CGE和∠CEB均不相等,相应边不成比例,
故△CEG和△CBE不相似,
故D选项错误,符合题意,
故选:D.
【点睛】本题考查了三角形全等的判定,三角形中位线性质应用,相似三角形的判定,熟练掌握相关性质、定理是解题的关键.
12.(2024 宁夏)如图,在Rt△ABC中,∠ABC=90°,AB=3cm,BC=2cm,点A在直线l1上,点B,C在直线l2上,l1∥l2,动点P从点A出发沿直线l1以1cm/s的速度向右运动,设运动时间为t s.
下列结论:
①当t=2s时,四边形ABCP的周长是10cm;
②当t=4s时,点P到直线l2的距离等于5cm;
③在点P运动过程中,△PBC的面积随着t的增大而增大;
④若点D,E分别是线段PB,PC的中点,在点P运动过程中,线段DE的长度不变.
其中正确的是( )
A.①④ B.②③ C.①③ D.②④
【点拨】①根据t=2s时得出四边形ABCP为矩形,据此可解决问题.
②根据“平行线间的距离处处相等”即可解决问题.
③根据②中的发现即可解决问题.
④利用三角形的中位线定理即可解决问题.
【解析】解:①当t=2s时,
AP=2cm,
则AP=BC.
又因为AP∥BC,∠ABC=90°,
所以四边形ABCP是矩形,
所以PC=AB=3cm,
所以四边形ABCP的周长为:2×(2+3)=10(cm).
故①正确.
因为“平行线间的距离处处相等”,AB=3cm,∠ABC=90°,
所以直线l1与直线l2之间的距离是3cm,
所以当t=4s时,点P到直线l2的距离仍然是3cm.
故②错误.
由上述过程可知,
点P到BC的距离为定值3cm,
即△PBC的BC边上的高为3cm,
又因为BC=2cm,
所以△PBC的面积为定值.
故③错误.
因为点D,E分别是线段PB,PC的中点,
所以DE是△PBC的中位线,
所以DE=(cm),
即线段DE的长度不变.
故④正确.
故选:A.
【点睛】本题主要考查了三角形面积及三角形的中位线定理,熟知三角形的中位线定理及三角形的面积公式是解题的关键.
二.填空题
13.(2024 上饶一模)将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为 75° .
【点拨】根据平角的定义得∠2+60°+45°=180°,得∠2=75°,根据平行线的性质可得答案.
【解析】解:如图,
∵∠2+60°+45°=180°,
∴∠2=75°,
∵直尺的上下两边平行,
∴∠1=∠2=75°,
故答案为:75°.
【点睛】本题主要考查了平行线的性质,平角的定义,熟练掌握三角板各角度数以及平行线的性质是解题的关键.
14.(2024 海南)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=40cm,当跷跷板的一端A着地时,另一端B离地面的高度为 80 cm.
【点拨】判断出OD是△ABE的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BE=2OM.
【解析】解:∵O是AB的中点,OM垂直于地面,BE垂直于地面,
∴OM是△ABE的中位线,
∴BE=2OM=2×40=80(cm),
另一端B离地面的高度为80cm,
故答案为:80.
【点睛】本题考查了三角形中位线定理,熟记定理是解题的关键.
15.(2025 鹿城区校级一模)如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= 1 .
【点拨】根据三角形中位线定理得到DE=BC=3,DE∥BC,根据角平分线的定义、平行线的性质得到∠DBF=∠DFB,得到DF=BD=2,计算即可.
【解析】解:∵点D、E分别为AB,AC的中点,AB=4,
∴DE是△ABC的中位线,BD=AB=2,
∴DE=BC=3,DE∥BC,
∴∠DFB=∠FBC,
∵BF平分∠ABC,
∴∠DFB=∠FBC,
∴∠DBF=∠DFB,
∴DF=BD=2,
∴EF=DE﹣DF=3﹣2=1,
故答案为:1.
【点睛】本题主要考查三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半.
16.(2024 湖南模拟)已知a,b,c是一个三角形的三边,且a,b满足.则c的取值范围是 1<c<3 .
【点拨】根据非负数的性质列式求出a、b,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求解即可.
【解析】解:∵
∴a﹣1=0,b﹣2=0,
解得a=1,b=2,
∵2﹣1=1,1+2=3,
∴1<c<3.
故答案为:1<c<3.
【点睛】本题主要考查的是三角形三边关系,非负数的性质,熟知三角形两边之和大于第三边;三角形的两边差小于第三边是解题的关键.
三.解答题
17.(2024 香洲区校级一模)已知如图,△ABC过点A作∠DAE=∠BAC,且AB∥DE,∠1=∠2.
(1)求证AD∥BC;
(2)若已知AE平分∠BAC,∠C=40°,求∠BAD的度数.
【点拨】(1)根据平行线的性质得出∠BAC=∠1,求出∠DAE=∠2,根据平行线的判定得出即可;
(2)根据角平分线的定义得出∠BAE=∠CAE,根据∠DAE=∠BEA求出∠BAE=∠EAC=∠DAC,根据平行线的性质得出∠C=∠DAC,求出∠C=∠BAE=∠DAC=40°,即可得出答案.
【解析】(1)证明:∵AB∥DE,
∴∠BAC=∠1,
∵∠1=∠2,
∴∠BAC=∠1,
∵∠DAE=∠BAC,
∴∠DAE=∠2,
∴AD∥BC;
(2)解:∵AD∥BC,
∵∠DAE=∠BEA,
∴∠BAE=∠EAC=∠DAC,
∵AD∥BC,
∴∠C=∠DAC,
∴∠C=∠BAE=∠DAC=40°,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=80°,
∴∠BAD=∠BAC+∠CAD=120°.
【点睛】本题考查了平行线的性质和判定,角平分线的定义等知识点,能灵活运用平行线的性质和判定进行推理是解此题的关键.
18.(2024 大埔县一模)如图,在△ABC中,AB=AC,AD⊥BC于点D,点E为AB的中点,连结DE.已知BC=10,AD=12,求BD,DE的长.
【点拨】根据等腰三角形的性质求出,根据勾股定理求出AB=13,
【解析】解∵AB=AC,AD⊥BC于点D,
∴,
∵BC=10,
∴BD=5,
∵AD⊥BC于点D,
∴∠ADB=90°,
在Rt△ABD中,AB2=AD2+BD2,
∵AD=12,
∴,
∵E为AB的中点,D点为BC的中点,
∴.
【点睛】此题考查了三角形中位线的判定与性质、等腰三角形的性质,熟记三角形中位线的判定与性质、等腰三角形的性质是解题的关键.
19.(2024 潍城区二模)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种
证明方法.
已知:如图甲, △ABC .
求证:∠A+∠B+∠C=180°.
证明:如图乙,作BC的延长线CD,在△ABC外部,以CA为一边,作∠ACE=∠A.
所以,CE∥AB(内错角相等,两直线平行).
所以,∠B=∠ECD( 两直线平行,同位角相等 ).
因为,∠ACB,∠ACE,∠ECD组成一个平角,
所以,∠ACB+∠ACE+∠ECD=180°(平角的定义),
所以,∠ACB+∠A+∠B=180°( 等量代换 ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
【点拨】(1)在△ABC外部,以CA为一边,作∠ACE=∠A.根据平行线的判定与性质及平角定义求解即可;
(2)过点A作AD∥BC,根据平行线的性质∠DAC=∠C,∠BAD+∠B=180°,由此证明即可.
【解析】解:(1)已知:如图甲,△ABC.
求证:∠A+∠B+∠C=180°.
证明:如图乙,作BC的延长线CD,在△ABC外部,以CA为一边,作∠ACE=∠A.
所以,CE∥AB(内错角相等,两直线平行).
所以,∠B=∠ECD(两直线平行,同位角相等).
因为,∠ACB,∠ACE,∠ECD组成一个平角,
所以,∠ACB+∠ACE+∠ECD=180°(平角的定义),
所以,∠ACB+∠A+∠B=180°(等量代换).
故答案为:△ABC;两直线平行,同位角相等;等量代换;
(2)如图丙,过点A作AD∥BC,
∵AD∥BC,
∴∠DAC=∠C(两直线平行,内错角相等).
∠BAD+∠B=180°(两直线平行,同旁内角互补).
即∠BAC+∠DAC+∠B=180°.
∴∠BAC+∠B+∠C=180°.
【点睛】本题考查了三角形内角和定理,平行线的判定与性质,熟练掌握三角形内角和定理的证明是解题的关键.
20.(2024 青岛一模)【探究1】
如图1,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= 33 °;
【探究2】
如图2,∠BAD的三等分线AE与∠BCD的三等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= 44 °;
【探究3】
如图3,∠BAD的n等分线AE与∠BCD的n等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=x°,∠ADC=y°,则∠AEC= =(x+y) °(用含x,y,n的式子表示).
【点拨】【探究1】过点E作EF∥AB,先证AB∥EF∥CD得∠FEA=∠BAE,∠FEC=∠DCE,则∠AEC=∠BAE+∠DCE,再根据AB∥CD及角平分线的定义得∠BAE=∠BAD=18°,∠DCE=∠BCD=15°,由此可得∠AEC的度数;
【探究2】同理可证∠AEC=∠BAE+∠DCE,再根据AB∥CD及已知条件得∠BAE=∠BAD=24°,∠DCE=∠BCD=20°,由此可得∠AEC的度数;
【探究3】同理可证∠AEC=∠BAE+∠DCE,再根据AB∥CD及已知条件得∠BAE=∠BD=y°,∠DCE=∠BCD=x°由此可得∠AEC的度数.
【解析】解:【探究1】过点E作EF∥AB,如图1所示:
∵EF∥AB,AB∥CD,
∴AB∥EF∥CD,
∴∠FEA=∠BAE,∠FEC=∠DCE,
∴∠FEA+∠FEC=∠BAE+∠DCE,
即∠AEC=∠BAE+∠DCE,
∵AB∥CD,
∴∠BCD=∠ABC=30°,∠BAD=∠ADC=36°,
∵AE平分BAD、CE平分∠BCD,
∴∠BAE=∠BAD=×36°=18°,∠DCE=∠BCD=×30°=15°,
∴∠AEC=∠FEC+∠FEA=18°+15°=33°;
【探究2】同理可证:∠AEC=∠BAE+∠DCE,
∵AB∥CD,
∴∠BCD=∠ABC=30°,∠BAD=∠ADC=36°,
∵∠EAD=∠BAD,∠BCE=∠BCD,
∴∠BAE=∠BAD=×36°=24°,∠DCE=∠BCD=×30°=20°,
∴∠AEC=∠BAE+∠DCE=24°+20°=44°;
【探究3】同理可证:∠AEC=∠BAE+∠DCE,
∵AB∥CD,
∴∠BCD=∠ABC=x°,∠BAD=∠ADC=y°,
∵∠EAD=∠BAD,∠BCE=∠BCD,
∠BAE=∠BD=y°,∠DCE=∠BCD=x°
∴∠AEC=∠BAE+∠DCE=y°+x°=(x+y)°.
【点睛】此题主要考查了平行线的性质,列代数式,准确识图,熟练掌握平行线的性质是解决问题的关键.
21.(2024 柯桥区模拟)问题提出:
(1)如图①,在△ABC中,点M,N分别是AB,AC的中点,若BC=6,则MN的长为 3 .
问题探究:
(2)如图②,在正方形ABCD中,AD=6,点E为AD上的靠近点A的三等分点,点F为AB上的动点,将△AEF折叠,点A的对应点G,求CG的最小值.
问题解决:
(3)如图③,某地要规划一个五边形艺术中心ABCDE,已知∠ABC=120°,∠BCD=60°,AB=AE=20m,BC=CD=40m,点C处为参观入口,DE的中点P处规划为“优秀”作品展台,求点C与点P之间的最小距离.
【点拨】(1)由三角形中位线定理可得出答案;
(2)由折叠得:AE=EG,得出点G在以点E为圆心,AE长为半径的⊙E上运动,由勾股定理求出CE的长,则可得出答案;
(3)延长DC至点F,使CF=CD,连接EF,求出AG=AB+BG=60m.过点F作FH⊥AG交AG延长线于点H,由勾股定理求出AF的长,则可得出答案.
【解析】解:(1)∵点M,N分别是AB,AC的中点,
∴MN=BC,
∵BC=6,
∴MN=3,
故答案为:3;
(2)∵在正方形ABCD中,AD=6,点E为AD上的靠近点A的三等分点,
∴AE=2,DE=4,CD=AD=6,∠D=90°.
由折叠得:AE=EG,
∴点G在以点E为圆心,AE长为半径的⊙E上运动,
作⊙E,连接CE交⊙E于点H,如图②,
∴CG≥CE﹣EG,
∴当点C,E,G三点共线,即点G和点H重合时,CG取得最小值,最小值为CH的长.
∵在Rt△CDE中,CE===,
∴CG的最小值为;
(3)如图③,延长DC至点F,使CF=CD,连接EF,
∵点P为DE的中点,点C为DF的中点,
∴PC为△DEF的中位线,
∴PC=,
∴当EF最小时,PC最小,
由AB=AE,可看作点E在以点A为圆心,AB长为半径的圆上,连接AF,
设AF与⊙A的交点为点E';则EF的最小值为E'F的长.过点F作FG∥BC交AB的延长线于点G,
∴∠ABC=∠FGB=120°,
∵∠ABC=120°,∠BCD=60°,
∴∠ABC+∠BCD=180°,
∴CF∥BG,
∴四边形BCFG为平行四边形,
∴CF=BG=40m,BC=FG=40m,
∴AG=AB+BG=20+40=60(m).
过点F作FH⊥AG交AG延长线于点H,
∴∠FGH=60°,
在Rt△FHG中,FH=FG=20m,HG=FG=20m,
∴AH=AG+HG=80m,
∴AF===20(m),
∴E'F=AF﹣AE'=20﹣20(m),
∴CP的最小值=E'F=(20﹣20)=10﹣10(m),
∴点C与点P之间的最小距离为 (10﹣10)m.
【点睛】本题主要考查了三角形中位线的判定和性质,解直角三角形,两点之间线段最短,解题的关键是:作辅助线构造三角形中位线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题16 三角形
一.选择题
1.(2024 湖南三模)下列各组长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,1,2 C.1,2,2 D.1,5,7
2.(2024 拱墅区一模)王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
3.(2024 鄞州区模拟)如图,直线l1∥l2,以直线l2上的点A为圆心适当长为半径画弧,分别交直线l1、l2于点B、C,连结AB、BC.若∠ACB=68°,则∠1的度数为( )
A.22° B.32° C.44° D.68°
4.(2024 桥西区模拟)平面内,将长分别为1,1,3,x的线段,首尾顺次相接组成凸四边形(如图),x可能是( )
A.1 B.3 C.5 D.7
5.(2024 山西模拟)为了比较与的大小,小亮先画了一条数轴,然后在原点O处作了一条垂线段OA,且OA=1,点B表示的数是2,点C表示的数为3,连接AB,AC,由AB+BC>AC推出,这里小亮用到的数学思想是( )
A.统计思想 B.数形结合 C.模型思想 D.分类讨论
6.(2024 汉川市模拟)已知△ABC中,其中有两边长是2和5,且△ABC的第三边长是偶数,则此三角形的周长为( )
A.11 B.12 C.13 D.11或13
7.(2024 重庆模拟)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
8.(2024 瑶海区一模)如图,在△ABC中,∠B+∠C=110°,AM平分∠BAC,交BC于点M,MN∥AB,交AC于点N,则∠AMN的大小是( )
A.30° B.35° C.40° D.55°
9.(2024 肥东县模拟)如图,将一副三角板的直角顶点重合并部分重叠,若∠BOD=20°,则∠AEC的度数为( )
A.30° B.35° C.40° D.45°
10.(2024 榆阳区二模)将一副三角板和一个直尺按如图所示的位置摆放,直角边BC与直尺的一边重合,点E在AC上,∠ABC=∠D=90°,∠A=30°,∠DEC=45°,则∠1的度数为( )
A.75° B.70° C.65° D.60°
11.(2024 西宁)如图,在△ABC中,AD是角平分线,BE是中线,AD=BE,且AD⊥BE,垂足为F,G为DC的中点,连接DE,EG.下列结论错误的是( )
A.△AFB≌△AFE B.∠ADB=∠ADE C.FD=BE D.△CEG~△CBE
12.(2024 宁夏)如图,在Rt△ABC中,∠ABC=90°,AB=3cm,BC=2cm,点A在直线l1上,点B,C在直线l2上,l1∥l2,动点P从点A出发沿直线l1以1cm/s的速度向右运动,设运动时间为t s.
下列结论:
①当t=2s时,四边形ABCP的周长是10cm;
②当t=4s时,点P到直线l2的距离等于5cm;
③在点P运动过程中,△PBC的面积随着t的增大而增大;
④若点D,E分别是线段PB,PC的中点,在点P运动过程中,线段DE的长度不变.
其中正确的是( )
A.①④ B.②③ C.①③ D.②④
二.填空题
13.(2024 上饶一模)将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为 .
14.(2024 海南)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=40cm,当跷跷板的一端A着地时,另一端B离地面的高度为 cm.
15.(2025 鹿城区校级一模)如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= .
16.(2024 湖南模拟)已知a,b,c是一个三角形的三边,且a,b满足.则c的取值范围是 .
三.解答题
17.(2024 香洲区校级一模)已知如图,△ABC过点A作∠DAE=∠BAC,且AB∥DE,∠1=∠2.
(1)求证AD∥BC;
(2)若已知AE平分∠BAC,∠C=40°,求∠BAD的度数.
18.(2024 大埔县一模)如图,在△ABC中,AB=AC,AD⊥BC于点D,点E为AB的中点,连结DE.已知BC=10,AD=12,求BD,DE的长.
19.(2024 潍城区二模)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种
证明方法.
已知:如图甲, .
求证:∠A+∠B+∠C=180°.
证明:如图乙,作BC的延长线CD,在△ABC外部,以CA为一边,作∠ACE=∠A.
所以,CE∥AB(内错角相等,两直线平行).
所以,∠B=∠ECD( ).
因为,∠ACB,∠ACE,∠ECD组成一个平角,
所以,∠ACB+∠ACE+∠ECD=180°(平角的定义),
所以,∠ACB+∠A+∠B=180°( ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
20.(2024 青岛一模)【探究1】
如图1,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= °;
【探究2】
如图2,∠BAD的三等分线AE与∠BCD的三等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= °;
【探究3】
如图3,∠BAD的n等分线AE与∠BCD的n等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=x°,∠ADC=y°,则∠AEC= °(用含x,y,n的式子表示).
21.(2024 柯桥区模拟)问题提出:
(1)如图①,在△ABC中,点M,N分别是AB,AC的中点,若BC=6,则MN的长为 .
问题探究:
(2)如图②,在正方形ABCD中,AD=6,点E为AD上的靠近点A的三等分点,点F为AB上的动点,将△AEF折叠,点A的对应点G,求CG的最小值.
问题解决:
(3)如图③,某地要规划一个五边形艺术中心ABCDE,已知∠ABC=120°,∠BCD=60°,AB=AE=20m,BC=CD=40m,点C处为参观入口,DE的中点P处规划为“优秀”作品展台,求点C与点P之间的最小距离.
答案与解析
一.选择题
1.(2024 湖南三模)下列各组长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,1,2 C.1,2,2 D.1,5,7
【点拨】根据三角形的任意两边的和大于第三边,任意两边之差小于第三边,只要把三边代入,看是否满足即可.
【解析】解:A.1+2=3,不能构成三角形,不合题意;
B.1+1=2,不能构成三角形,不合题意;
C..1+2>2,能构成三角形,符合题意;
D.1+5<7,不能构成三角形,不合题意.
故选:C.
【点睛】此题主要考查了三角形的三边关系,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.
2.(2024 拱墅区一模)王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线 C.高线 D.以上都不是
【点拨】根据三角形的中线把三角形分为面积相等的两部分解答.
【解析】解:由三角形的面积公式可知,三角形的中线把三角形分为面积相等的两部分,
∴他所作的线段AD应该是△ABC的中线,
故选:B.
【点睛】本题考查的是三角形的面积计算,掌握三角形的中线把三角形分为面积相等的两部分是解题的关键.
3.(2024 鄞州区模拟)如图,直线l1∥l2,以直线l2上的点A为圆心适当长为半径画弧,分别交直线l1、l2于点B、C,连结AB、BC.若∠ACB=68°,则∠1的度数为( )
A.22° B.32° C.44° D.68°
【点拨】由题意可得AB=AC,则有∠ABC=∠ACB=68°,再利用三角形的内角和即可求∠1的度数.
【解析】解:∵以直线l2上的点A为圆心适当长为半径画弧,分别交直线l1、l2于点B、C,
∴AB=AC,
∴∠ABC=∠ACB=68°,
在△ABC中,∠1=180°﹣∠ABC﹣∠ACB=44°.
故选:C.
【点睛】本题主要考查三角形的内角和定理,等腰三角形的性质,解答的关键是由题意得到AB=AC.
4.(2024 桥西区模拟)平面内,将长分别为1,1,3,x的线段,首尾顺次相接组成凸四边形(如图),x可能是( )
A.1 B.3 C.5 D.7
【点拨】由三角形三边关系定理得到2<AC<4,AC﹣1<x<AC+1,因此1<x<5,即可得到答案.
【解析】解:连接AC,
在△ACD中,3﹣1<AC<3+1,
∴2<AC<4,
在△ABC中,AC﹣1<x<AC+1,
∴1<x<5,
∴x可能是3.
故选:B.
【点睛】本题考查三角形的三边关系,关键是连接AC,应用三角形的三边关系定理来解决问题.
5.(2024 山西模拟)为了比较与的大小,小亮先画了一条数轴,然后在原点O处作了一条垂线段OA,且OA=1,点B表示的数是2,点C表示的数为3,连接AB,AC,由AB+BC>AC推出,这里小亮用到的数学思想是( )
A.统计思想 B.数形结合 C.模型思想 D.分类讨论
【点拨】由数形结合思想,即可得到答案.
【解析】解:这里小亮用到的数学思想是数形结合.
故选:B.
【点睛】本题考查三角形三边关系,实数与数轴,实数大小比较,数学思想,关键是掌握数形结合思想.
6.(2024 汉川市模拟)已知△ABC中,其中有两边长是2和5,且△ABC的第三边长是偶数,则此三角形的周长为( )
A.11 B.12 C.13 D.11或13
【点拨】三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边,设第三边长x,得到3<x<7,由△ABC的第三边长是偶数,得到x=4或6,于是得到此三角形的周长.
【解析】解:设第三边长x,
∴5﹣2<x<5+2,
∴3<x<7,
∵△ABC的第三边长是偶数,
∴x=4或6,
∴此三角形的周长为2+5+4=11或2+5+6=13.
故选:D.
【点睛】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
7.(2024 重庆模拟)如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90° C.∠BAF=∠CAF D.S△ABC=2S△ABF
【点拨】根据三角形的角平分线、中线和高的概念判断.
【解析】解:∵AF是△ABC的中线,
∴BF=CF,A说法正确,不符合题意;
∵AD是高,
∴∠ADC=90°,
∴∠C+∠CAD=90°,B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE,而∠BAF与∠CAF不一定相等,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF,D说法正确,不符合题意;
故选:C.
【点睛】本题考查的是三角形的角平分线、中线和高,掌握它们的概念是解题的关键.
8.(2024 瑶海区一模)如图,在△ABC中,∠B+∠C=110°,AM平分∠BAC,交BC于点M,MN∥AB,交AC于点N,则∠AMN的大小是( )
A.30° B.35° C.40° D.55°
【点拨】先根据已知条件和三角形的内角和为180°,求出∠BAC的度数,再根据已知条件和角平分线的定义,求出∠BAM,最后根据MN∥AB,求出∠AMN即可.
【解析】解:∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣(∠B+∠C)=180°﹣110°=70°,
∵AM平分∠BAC,
∴∠BAM=,
∵MN∥AB,
∴∠AMN=∠BAM=35°,
故选:B.
【点睛】本题主要考查了三角形内角和定理和平行线的性质,解题关键是熟练掌握三角形三个内角的和是180°和平行线的性质.
9.(2024 肥东县模拟)如图,将一副三角板的直角顶点重合并部分重叠,若∠BOD=20°,则∠AEC的度数为( )
A.30° B.35° C.40° D.45°
【点拨】根据三角形内角和定理求出∠B的度数,进而根据三角形外角的性质求出∠AFO的度数,再由三角形外角的性质求出∠DEF的度数,最后根据对顶角相等即可得到答案.
【解析】解:如图,
由题意得,∠B=180°﹣30°﹣90°=60°,
∵∠BOD=20°,
∴∠AFO=∠BOD+∠B=80°,
∴∠DEF=∠AFO﹣∠D=35°,
∴∠AEC=∠DEB=35°,
故选:B.
【点睛】本题主要考查了三角形内角和定理,三角形外角的性质,熟练掌握各知识点是解题的关键.
10.(2024 榆阳区二模)将一副三角板和一个直尺按如图所示的位置摆放,直角边BC与直尺的一边重合,点E在AC上,∠ABC=∠D=90°,∠A=30°,∠DEC=45°,则∠1的度数为( )
A.75° B.70° C.65° D.60°
【点拨】在图中标记∠2,利用三角形内角和定理,可求出∠ACB及∠DCE的度数,结合邻补角互补,可求出∠2的度数,由直尺的对边平行,再利用“两直线平行,同位角相等”,即可求出∠1的度数.
【解析】解:在图中标记∠2,如图所示.
∵∠ACB=180°﹣90°﹣30°=60°,∠DCE=180°﹣90°﹣45°=45°,
∴∠2=180°﹣∠ACB﹣∠DCE=180°﹣60°﹣45°=75°.
∵直尺的对边平行,
∴∠1=∠2=75°.
故选:A.
【点睛】本题考查了三角形内角和定理、平行线的性质以及余角和补角,利用三角形内角和定理及邻补角互补,找出∠2的度数是解题的关键.
11.(2024 西宁)如图,在△ABC中,AD是角平分线,BE是中线,AD=BE,且AD⊥BE,垂足为F,G为DC的中点,连接DE,EG.下列结论错误的是( )
A.△AFB≌△AFE B.∠ADB=∠ADE C.FD=BE D.△CEG~△CBE
【点拨】根据三角形全等可判断A,B两选项,根据三角形中位线性质,可判断C选项,以及相似三角形的判断,从而得到结果.
【解析】解:∵AD是角平分线,
∴∠BAD=∠EAD,
∵AD⊥BE,
∴∠AFB=∠AFE=90°,
又∵AF=AF,
∴△AFB≌△AFE(ASA),
故A选项正确,不符合题意;
∵△AFB≌△AFE,
∴AB=AE,
∵∠BAD=∠EAD,AD=AD,
∴△ADB≌△ADE(SAS),
∴∠ADB=∠ADE,
故B选项正确,不符合题意;
∵BE是中线,
∴CE=EA,
∵G为DC的中点,
∴CG=GD,
∴EG是△CAD中位线,
∴EG=AD,EG∥AD,
∴,
又∵△AFB≌△AFE,
∴BF=FE,
∴BD=GD,
∴DF是△BEG的中位线,
∴DF=EG,
∴DF=AD,
∵AD=BE,
∴DF=BE,
故C选项正确,不符合题意;
在△CEG和△CBE中,∠C为公共角,
但∠CEG和∠CBE,∠CGE和∠CEB均不相等,相应边不成比例,
故△CEG和△CBE不相似,
故D选项错误,符合题意,
故选:D.
【点睛】本题考查了三角形全等的判定,三角形中位线性质应用,相似三角形的判定,熟练掌握相关性质、定理是解题的关键.
12.(2024 宁夏)如图,在Rt△ABC中,∠ABC=90°,AB=3cm,BC=2cm,点A在直线l1上,点B,C在直线l2上,l1∥l2,动点P从点A出发沿直线l1以1cm/s的速度向右运动,设运动时间为t s.
下列结论:
①当t=2s时,四边形ABCP的周长是10cm;
②当t=4s时,点P到直线l2的距离等于5cm;
③在点P运动过程中,△PBC的面积随着t的增大而增大;
④若点D,E分别是线段PB,PC的中点,在点P运动过程中,线段DE的长度不变.
其中正确的是( )
A.①④ B.②③ C.①③ D.②④
【点拨】①根据t=2s时得出四边形ABCP为矩形,据此可解决问题.
②根据“平行线间的距离处处相等”即可解决问题.
③根据②中的发现即可解决问题.
④利用三角形的中位线定理即可解决问题.
【解析】解:①当t=2s时,
AP=2cm,
则AP=BC.
又因为AP∥BC,∠ABC=90°,
所以四边形ABCP是矩形,
所以PC=AB=3cm,
所以四边形ABCP的周长为:2×(2+3)=10(cm).
故①正确.
因为“平行线间的距离处处相等”,AB=3cm,∠ABC=90°,
所以直线l1与直线l2之间的距离是3cm,
所以当t=4s时,点P到直线l2的距离仍然是3cm.
故②错误.
由上述过程可知,
点P到BC的距离为定值3cm,
即△PBC的BC边上的高为3cm,
又因为BC=2cm,
所以△PBC的面积为定值.
故③错误.
因为点D,E分别是线段PB,PC的中点,
所以DE是△PBC的中位线,
所以DE=(cm),
即线段DE的长度不变.
故④正确.
故选:A.
【点睛】本题主要考查了三角形面积及三角形的中位线定理,熟知三角形的中位线定理及三角形的面积公式是解题的关键.
二.填空题
13.(2024 上饶一模)将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为 75° .
【点拨】根据平角的定义得∠2+60°+45°=180°,得∠2=75°,根据平行线的性质可得答案.
【解析】解:如图,
∵∠2+60°+45°=180°,
∴∠2=75°,
∵直尺的上下两边平行,
∴∠1=∠2=75°,
故答案为:75°.
【点睛】本题主要考查了平行线的性质,平角的定义,熟练掌握三角板各角度数以及平行线的性质是解题的关键.
14.(2024 海南)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=40cm,当跷跷板的一端A着地时,另一端B离地面的高度为 80 cm.
【点拨】判断出OD是△ABE的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BE=2OM.
【解析】解:∵O是AB的中点,OM垂直于地面,BE垂直于地面,
∴OM是△ABE的中位线,
∴BE=2OM=2×40=80(cm),
另一端B离地面的高度为80cm,
故答案为:80.
【点睛】本题考查了三角形中位线定理,熟记定理是解题的关键.
15.(2025 鹿城区校级一模)如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= 1 .
【点拨】根据三角形中位线定理得到DE=BC=3,DE∥BC,根据角平分线的定义、平行线的性质得到∠DBF=∠DFB,得到DF=BD=2,计算即可.
【解析】解:∵点D、E分别为AB,AC的中点,AB=4,
∴DE是△ABC的中位线,BD=AB=2,
∴DE=BC=3,DE∥BC,
∴∠DFB=∠FBC,
∵BF平分∠ABC,
∴∠DFB=∠FBC,
∴∠DBF=∠DFB,
∴DF=BD=2,
∴EF=DE﹣DF=3﹣2=1,
故答案为:1.
【点睛】本题主要考查三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半.
16.(2024 湖南模拟)已知a,b,c是一个三角形的三边,且a,b满足.则c的取值范围是 1<c<3 .
【点拨】根据非负数的性质列式求出a、b,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求解即可.
【解析】解:∵
∴a﹣1=0,b﹣2=0,
解得a=1,b=2,
∵2﹣1=1,1+2=3,
∴1<c<3.
故答案为:1<c<3.
【点睛】本题主要考查的是三角形三边关系,非负数的性质,熟知三角形两边之和大于第三边;三角形的两边差小于第三边是解题的关键.
三.解答题
17.(2024 香洲区校级一模)已知如图,△ABC过点A作∠DAE=∠BAC,且AB∥DE,∠1=∠2.
(1)求证AD∥BC;
(2)若已知AE平分∠BAC,∠C=40°,求∠BAD的度数.
【点拨】(1)根据平行线的性质得出∠BAC=∠1,求出∠DAE=∠2,根据平行线的判定得出即可;
(2)根据角平分线的定义得出∠BAE=∠CAE,根据∠DAE=∠BEA求出∠BAE=∠EAC=∠DAC,根据平行线的性质得出∠C=∠DAC,求出∠C=∠BAE=∠DAC=40°,即可得出答案.
【解析】(1)证明:∵AB∥DE,
∴∠BAC=∠1,
∵∠1=∠2,
∴∠BAC=∠1,
∵∠DAE=∠BAC,
∴∠DAE=∠2,
∴AD∥BC;
(2)解:∵AD∥BC,
∵∠DAE=∠BEA,
∴∠BAE=∠EAC=∠DAC,
∵AD∥BC,
∴∠C=∠DAC,
∴∠C=∠BAE=∠DAC=40°,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=80°,
∴∠BAD=∠BAC+∠CAD=120°.
【点睛】本题考查了平行线的性质和判定,角平分线的定义等知识点,能灵活运用平行线的性质和判定进行推理是解此题的关键.
18.(2024 大埔县一模)如图,在△ABC中,AB=AC,AD⊥BC于点D,点E为AB的中点,连结DE.已知BC=10,AD=12,求BD,DE的长.
【点拨】根据等腰三角形的性质求出,根据勾股定理求出AB=13,
【解析】解∵AB=AC,AD⊥BC于点D,
∴,
∵BC=10,
∴BD=5,
∵AD⊥BC于点D,
∴∠ADB=90°,
在Rt△ABD中,AB2=AD2+BD2,
∵AD=12,
∴,
∵E为AB的中点,D点为BC的中点,
∴.
【点睛】此题考查了三角形中位线的判定与性质、等腰三角形的性质,熟记三角形中位线的判定与性质、等腰三角形的性质是解题的关键.
19.(2024 潍城区二模)三角形的内角和定理是初中数学学习中的一个重要定理,下面给出了该定理的一种
证明方法.
已知:如图甲, △ABC .
求证:∠A+∠B+∠C=180°.
证明:如图乙,作BC的延长线CD,在△ABC外部,以CA为一边,作∠ACE=∠A.
所以,CE∥AB(内错角相等,两直线平行).
所以,∠B=∠ECD( 两直线平行,同位角相等 ).
因为,∠ACB,∠ACE,∠ECD组成一个平角,
所以,∠ACB+∠ACE+∠ECD=180°(平角的定义),
所以,∠ACB+∠A+∠B=180°( 等量代换 ).
(1)请将上面的“已知”和推理“依据”补充完整;
(2)该定理有多种证明方法,请再写出一种证明方法.
【点拨】(1)在△ABC外部,以CA为一边,作∠ACE=∠A.根据平行线的判定与性质及平角定义求解即可;
(2)过点A作AD∥BC,根据平行线的性质∠DAC=∠C,∠BAD+∠B=180°,由此证明即可.
【解析】解:(1)已知:如图甲,△ABC.
求证:∠A+∠B+∠C=180°.
证明:如图乙,作BC的延长线CD,在△ABC外部,以CA为一边,作∠ACE=∠A.
所以,CE∥AB(内错角相等,两直线平行).
所以,∠B=∠ECD(两直线平行,同位角相等).
因为,∠ACB,∠ACE,∠ECD组成一个平角,
所以,∠ACB+∠ACE+∠ECD=180°(平角的定义),
所以,∠ACB+∠A+∠B=180°(等量代换).
故答案为:△ABC;两直线平行,同位角相等;等量代换;
(2)如图丙,过点A作AD∥BC,
∵AD∥BC,
∴∠DAC=∠C(两直线平行,内错角相等).
∠BAD+∠B=180°(两直线平行,同旁内角互补).
即∠BAC+∠DAC+∠B=180°.
∴∠BAC+∠B+∠C=180°.
【点睛】本题考查了三角形内角和定理,平行线的判定与性质,熟练掌握三角形内角和定理的证明是解题的关键.
20.(2024 青岛一模)【探究1】
如图1,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= 33 °;
【探究2】
如图2,∠BAD的三等分线AE与∠BCD的三等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=30°,∠ADC=36°,则∠AEC= 44 °;
【探究3】
如图3,∠BAD的n等分线AE与∠BCD的n等分线CE交于点E,∠EAD=∠BAD,∠BCE=∠BCD,AB∥CD,∠ABC=x°,∠ADC=y°,则∠AEC= =(x+y) °(用含x,y,n的式子表示).
【点拨】【探究1】过点E作EF∥AB,先证AB∥EF∥CD得∠FEA=∠BAE,∠FEC=∠DCE,则∠AEC=∠BAE+∠DCE,再根据AB∥CD及角平分线的定义得∠BAE=∠BAD=18°,∠DCE=∠BCD=15°,由此可得∠AEC的度数;
【探究2】同理可证∠AEC=∠BAE+∠DCE,再根据AB∥CD及已知条件得∠BAE=∠BAD=24°,∠DCE=∠BCD=20°,由此可得∠AEC的度数;
【探究3】同理可证∠AEC=∠BAE+∠DCE,再根据AB∥CD及已知条件得∠BAE=∠BD=y°,∠DCE=∠BCD=x°由此可得∠AEC的度数.
【解析】解:【探究1】过点E作EF∥AB,如图1所示:
∵EF∥AB,AB∥CD,
∴AB∥EF∥CD,
∴∠FEA=∠BAE,∠FEC=∠DCE,
∴∠FEA+∠FEC=∠BAE+∠DCE,
即∠AEC=∠BAE+∠DCE,
∵AB∥CD,
∴∠BCD=∠ABC=30°,∠BAD=∠ADC=36°,
∵AE平分BAD、CE平分∠BCD,
∴∠BAE=∠BAD=×36°=18°,∠DCE=∠BCD=×30°=15°,
∴∠AEC=∠FEC+∠FEA=18°+15°=33°;
【探究2】同理可证:∠AEC=∠BAE+∠DCE,
∵AB∥CD,
∴∠BCD=∠ABC=30°,∠BAD=∠ADC=36°,
∵∠EAD=∠BAD,∠BCE=∠BCD,
∴∠BAE=∠BAD=×36°=24°,∠DCE=∠BCD=×30°=20°,
∴∠AEC=∠BAE+∠DCE=24°+20°=44°;
【探究3】同理可证:∠AEC=∠BAE+∠DCE,
∵AB∥CD,
∴∠BCD=∠ABC=x°,∠BAD=∠ADC=y°,
∵∠EAD=∠BAD,∠BCE=∠BCD,
∠BAE=∠BD=y°,∠DCE=∠BCD=x°
∴∠AEC=∠BAE+∠DCE=y°+x°=(x+y)°.
【点睛】此题主要考查了平行线的性质,列代数式,准确识图,熟练掌握平行线的性质是解决问题的关键.
21.(2024 柯桥区模拟)问题提出:
(1)如图①,在△ABC中,点M,N分别是AB,AC的中点,若BC=6,则MN的长为 3 .
问题探究:
(2)如图②,在正方形ABCD中,AD=6,点E为AD上的靠近点A的三等分点,点F为AB上的动点,将△AEF折叠,点A的对应点G,求CG的最小值.
问题解决:
(3)如图③,某地要规划一个五边形艺术中心ABCDE,已知∠ABC=120°,∠BCD=60°,AB=AE=20m,BC=CD=40m,点C处为参观入口,DE的中点P处规划为“优秀”作品展台,求点C与点P之间的最小距离.
【点拨】(1)由三角形中位线定理可得出答案;
(2)由折叠得:AE=EG,得出点G在以点E为圆心,AE长为半径的⊙E上运动,由勾股定理求出CE的长,则可得出答案;
(3)延长DC至点F,使CF=CD,连接EF,求出AG=AB+BG=60m.过点F作FH⊥AG交AG延长线于点H,由勾股定理求出AF的长,则可得出答案.
【解析】解:(1)∵点M,N分别是AB,AC的中点,
∴MN=BC,
∵BC=6,
∴MN=3,
故答案为:3;
(2)∵在正方形ABCD中,AD=6,点E为AD上的靠近点A的三等分点,
∴AE=2,DE=4,CD=AD=6,∠D=90°.
由折叠得:AE=EG,
∴点G在以点E为圆心,AE长为半径的⊙E上运动,
作⊙E,连接CE交⊙E于点H,如图②,
∴CG≥CE﹣EG,
∴当点C,E,G三点共线,即点G和点H重合时,CG取得最小值,最小值为CH的长.
∵在Rt△CDE中,CE===,
∴CG的最小值为;
(3)如图③,延长DC至点F,使CF=CD,连接EF,
∵点P为DE的中点,点C为DF的中点,
∴PC为△DEF的中位线,
∴PC=,
∴当EF最小时,PC最小,
由AB=AE,可看作点E在以点A为圆心,AB长为半径的圆上,连接AF,
设AF与⊙A的交点为点E';则EF的最小值为E'F的长.过点F作FG∥BC交AB的延长线于点G,
∴∠ABC=∠FGB=120°,
∵∠ABC=120°,∠BCD=60°,
∴∠ABC+∠BCD=180°,
∴CF∥BG,
∴四边形BCFG为平行四边形,
∴CF=BG=40m,BC=FG=40m,
∴AG=AB+BG=20+40=60(m).
过点F作FH⊥AG交AG延长线于点H,
∴∠FGH=60°,
在Rt△FHG中,FH=FG=20m,HG=FG=20m,
∴AH=AG+HG=80m,
∴AF===20(m),
∴E'F=AF﹣AE'=20﹣20(m),
∴CP的最小值=E'F=(20﹣20)=10﹣10(m),
∴点C与点P之间的最小距离为 (10﹣10)m.
【点睛】本题主要考查了三角形中位线的判定和性质,解直角三角形,两点之间线段最短,解题的关键是:作辅助线构造三角形中位线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
