2025年浙江省中考数学一轮复习专题检测 专题18 等腰三角形(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题18 等腰三角形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 09:59:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题18 等腰三角形
一.选择题
1.(2024 宿迁二模)等腰三角形的一个内角为80°,则这个等腰三角形的底角为( )
A.80°或50° B.80° C.50° D.50°或20°
2.(2024 兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB=( )
A.100° B.115° C.130° D.145°
3.(2024 大荔县校级二模)如图,在△ABC中,点D是BC上一点.连接AD,已知AB=5,∠B=70°,∠C=35°,若∠BAD=40°,则CD的长为( )
A.4 B.5 C.6 D.7
4.(2024 邯山区校级四模)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD的夹角为( )
A.10° B.15° C.20° D.30°
5.(2024 黄岩区一模)如图,△ABC是等腰三角形,AB=AC,∠BAC是钝角.点D在底边BC上,连接AD,恰好把△ABC分割成两个等腰三角形,则∠B的度数是( )
A.30° B.36° C.45° D.60°
6.(2024 自贡)如图,等边△ABC钢架的立柱CD⊥AB于点D,AB长12m.现将钢架立柱缩短成DE,∠BED=60°.则新钢架减少用钢( )
A.(24﹣12)m B.(24﹣8)m C.(24﹣6)m D.(24﹣4)m
7.(2024 海宁市校级模拟)如图所示的△ABC,进行以下操作:①以A,B为圆心,大于AB为半径作圆弧,相交点D,E;②以A,C为圆心,大于AC为半径作圆弧,相交于点F,G.两直线DE,FG相交于△ABC外一点P,且分别交BC点M,N.若∠MAN=50°,则∠MPN等于( )
A.60° B.65° C.70° D.75°
8.(2024 山海关区一模)如图,在△ABC中,AB=AC,M为BC边上一点,且AM=AN,则∠BAM与∠NMC的关系一定成立的是( )
A.∠BAM=∠NMC B.∠BAM+∠NMC=∠BAC
C.∠BAM+∠NMC=∠B D.∠BAM=2∠NMC
9.(2024 花溪区一模)如图,在△ABC中,BC=7,∠ABC和∠ACB的平分线相交于点D,过点D作BC的平行线交AB于点E,交AC于点F,若△AEF的周长为14,则△ABC的周长是( )
A.14 B.19 C.21 D.23
10.(2024 天津一模)已知等边三角形ABC的边长为3,D为BC边上的一点(点D不与点B,C重合),过D点作AB边的垂线,交AB于点G,用x表示线段AG的长度,y表示Rt△GBD的面积,有下列结论:①<x<3;②DB=x;③y=(3﹣x)2,其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
二.填空题
11.(2024 嘉善县一模)已知等腰三角形的两边长是4和8,则这个三角形的周长是 .
12.(2024 贵州)如图,在△ABC中,以点A为圆心,线段AB的长为半径画弧,交BC于点D,连接AD.若AB=5,则AD的长为 .
13.(2024 镇江)如图,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC=8,CD=5,则BD= .
14.(2024 钱塘区三模)如图,△ABC为等边三角形,点D为BC延长线上一点.若,∠CAD=15°,则AB的长为 .
15.(2024 蒙阴县二模)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 .
16.(2024 萧县二模)如图,D,E,F是△ABC的边BC,AB,AC上的点,且满足DB=DE,DC=DF,DC=DF,∠BDF=∠CDE=135°,连接BF,CE,过点C作CH⊥AB,垂足为H.
(1)∠A的度数是 .
(2)若AH=5,AF=4,则EH= .
三.解答题
17.(2024 濠江区一模)如图,点C为∠AOB平分线上一点,CD∥OB交OA于点D.求证:△DOC是等腰三角形.
18.(2024 镇海区校级一模)如图,在△ABC中,D、E分别是△ABC边AB、AC上的点,已知DE∥BC且DB=DE.
(1)求证:BE是△ABC的角平分线;
(2)若∠A=65°,∠C=45°,求∠AEB的度数.
19.(2024 利川市校级模拟)如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
(2)求∠BQM的大小.
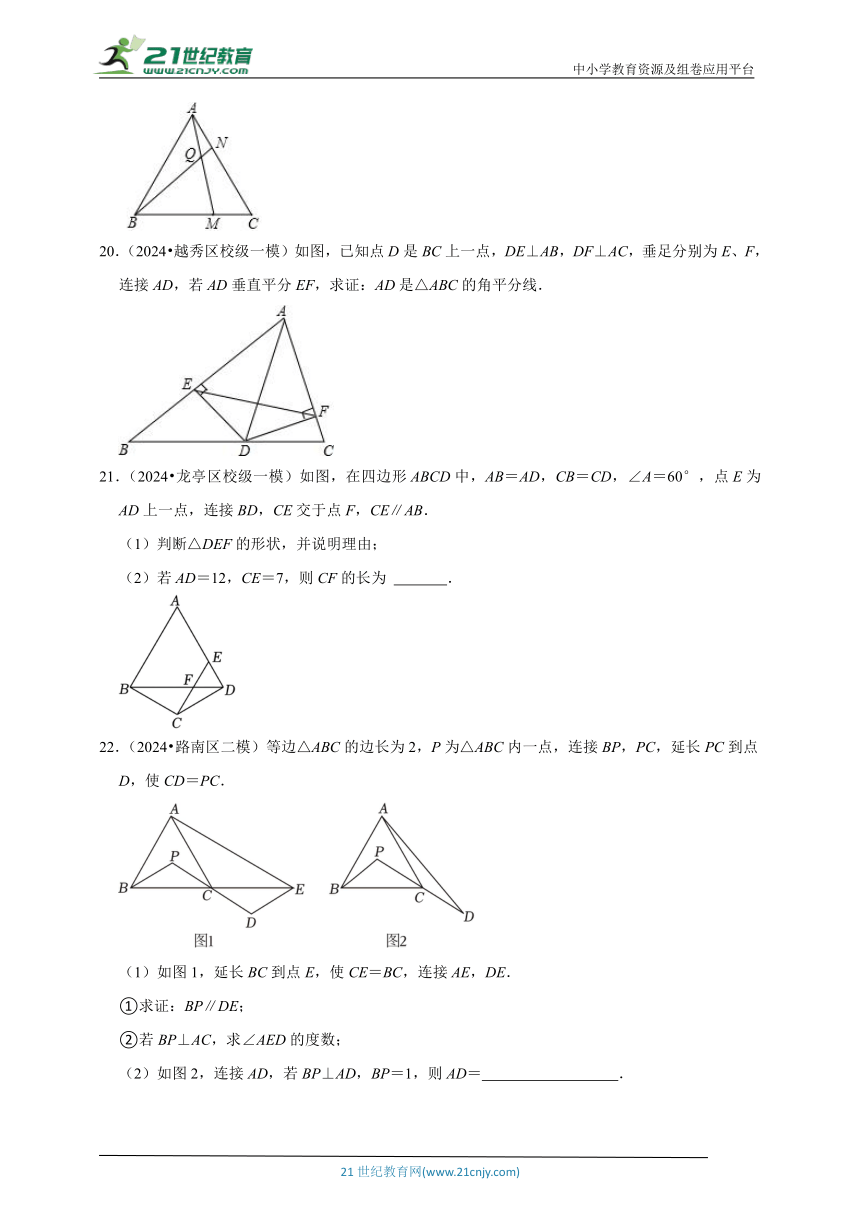
20.(2024 越秀区校级一模)如图,已知点D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F,连接AD,若AD垂直平分EF,求证:AD是△ABC的角平分线.
21.(2024 龙亭区校级一模)如图,在四边形ABCD中,AB=AD,CB=CD,∠A=60°,点E为AD上一点,连接BD,CE交于点F,CE∥AB.
(1)判断△DEF的形状,并说明理由;
(2)若AD=12,CE=7,则CF的长为 .
22.(2024 路南区二模)等边△ABC的边长为2,P为△ABC内一点,连接BP,PC,延长PC到点D,使CD=PC.
(1)如图1,延长BC到点E,使CE=BC,连接AE,DE.
①求证:BP∥DE;
②若BP⊥AC,求∠AED的度数;
(2)如图2,连接AD,若BP⊥AD,BP=1,则AD= .
答案与解析
一.选择题
1.(2024 宿迁二模)等腰三角形的一个内角为80°,则这个等腰三角形的底角为( )
A.80°或50° B.80° C.50° D.50°或20°
【点拨】由于不明确80°的角是等腰三角形的底角还是顶角,故应分80°的角是顶角和底角两种情况讨论.
【解析】解:分两种情况:
①当80°的角为等腰三角形的顶角时,
底角的度数=(180°﹣80°)÷2=50°;
②当80°的角为等腰三角形的底角时,其底角为80°,
故它的底角度数是50°或80°.
故选:A.
【点睛】本题考查的是等腰三角形的性质及三角形内角和定理;解答此题时要注意80°的角是顶角和底角两种情况,不要漏解,分类讨论是正确解答本题的关键.
2.(2024 兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB=( )
A.100° B.115° C.130° D.145°
【点拨】根据等边对等角得出∠B=∠C,根据∠BAC=130°即可求出∠C的度数,由DA⊥AC得出∠DAC=90°,从而求出∠ADC的度数,问题得解.
【解析】解:在△ABC中,AB=AC,
∴∠B=∠C,
∵∠BAC=130°,
∴∠B=∠C==25°,
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90°﹣25°=65°,
∴∠ADB=180°﹣∠ADC=180°﹣65°=115°,
故选:B.
【点睛】本题考查了等腰三角形的性质,三角形内角和定理,熟练掌握这些知识点是解题的关键.
3.(2024 大荔县校级二模)如图,在△ABC中,点D是BC上一点.连接AD,已知AB=5,∠B=70°,∠C=35°,若∠BAD=40°,则CD的长为( )
A.4 B.5 C.6 D.7
【点拨】根据三角形的面积好多了,等腰三角形的判定和性质定理,以及三角形外角的性质即可得到结论.
【解析】解:∵∠B=70°,∠BAD=40°,
∴∠ADB=180°﹣∠B﹣∠BAD=70°,
∴AD=AB=5,
∵∠ADB=∠CAD+∠C,
∴∠CAD=∠ADB﹣∠C=35°,
∴∠CAD=∠C,
∴CD=AD=5,
故选:B.
【点睛】本题考查了等腰三角形的判定和性质,三角形外角的性质,熟练掌握等腰三角形的判定和性质定理是解题的关键.
4.(2024 邯山区校级四模)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD的夹角为( )
A.10° B.15° C.20° D.30°
【点拨】延长AD与BC交于点E,根据等边三角形和等腰直角三角形性质得∠ABC=∠BAC=60°,∠CAD=45°,进而得∠BAD=105°,然后根据三角形内角和定理求出∠E即可.
【解析】解:延长AD与BC交于点E,如图所示:
∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
又∵△ACD为等腰直角三角形,AC=CD,
∴∠CAD=45°,
∴∠BAD=∠BAC+∠CAD=60°+45°=105°,
∴∠E=180°﹣(∠ABC+∠BAD)=180°﹣(60°+105°)=15°.
即直线BC与直线AD的夹角为15°.
故选:B.
【点睛】此题主要考查了据等边三角形和等腰直角三角形性质,三角形的内角和定理,熟练掌握等边三角形和等腰直角三角形性质,三角形的内角和定理是解决问题的关键.
5.(2024 黄岩区一模)如图,△ABC是等腰三角形,AB=AC,∠BAC是钝角.点D在底边BC上,连接AD,恰好把△ABC分割成两个等腰三角形,则∠B的度数是( )
A.30° B.36° C.45° D.60°
【点拨】由等腰三角形的性质得出∠B=∠C=∠BAD,∠ADC=∠DAC,根据三角形外角的性质得∠ADC=∠DAC=∠B+∠BAD=2∠B=2∠C,设∠C=x,在△ADC中,由三角形内角和定理得出方程,解方程即可.
【解析】解:∵AB=AC,AD,恰好把△ABC分割成两个等腰三角形,
∴∠B=∠C,∠B=∠BAD,∠ADC=∠DAC,
∵∠ADC=∠B+∠BAD,
∴∠ADC=∠DAC=∠B+∠BAD=2∠B=2∠C,
设∠C=x,
在△ADC中,∠CAD+∠ADC+∠C=180°,
即x+2x+2x=180°,
解得:x=36°,
∴∠C=36°,
∴∠B=36°,
故选:B.
【点睛】本题考查了等腰三角形的性质、三角形内角和定理、三角形的外角性质等知识,解题的关键是理解题意,学会利用方程去思考问题.
6.(2024 自贡)如图,等边△ABC钢架的立柱CD⊥AB于点D,AB长12m.现将钢架立柱缩短成DE,∠BED=60°.则新钢架减少用钢( )
A.(24﹣12)m B.(24﹣8)m C.(24﹣6)m D.(24﹣4)m
【点拨】根据特殊直角三角形求出DE,CD和BE的长,从而得出减少用钢的长度.
【解析】解:∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC=AC=12,BD=6,
∴CD=,
∵∠BED=60°,
∴DE=,BE=AE=,
∴减少用钢为(AB+AC+BC+CD)﹣(AE+BE+AB+DE)=AC+BC+CD﹣AE﹣BE﹣DE=24﹣(cm),
故选:D.
【点睛】本题考查了等边三角形的性质,特殊直角三角形的三边关系,掌握特殊角的三边关系是解题的关键.
7.(2024 海宁市校级模拟)如图所示的△ABC,进行以下操作:①以A,B为圆心,大于AB为半径作圆弧,相交点D,E;②以A,C为圆心,大于AC为半径作圆弧,相交于点F,G.两直线DE,FG相交于△ABC外一点P,且分别交BC点M,N.若∠MAN=50°,则∠MPN等于( )
A.60° B.65° C.70° D.75°
【点拨】根据作法知,DE、FG分别是AB、AC的垂直平分线,根据线段垂直平分线的性质得出AM=BM,AN=CN,AP=BP=CP,根据等腰三角形的性质得出∠ABM=∠BAM,∠ACN=∠CAN,∠ABP=∠BAP,∠ACP=∠CAP,∠APD=∠APB,∠APF=∠APC,根据三角形内角和定理求出∠ANM+∠AMN=130°,根据三角形外角性质及角的和差求出∠BAC=115°,根据四边形内角和定理求出∠BPC=130°,再根据∠MPN=∠APD+∠APF求解即可.
【解析】解:如图,连接AP、BP、CP,
根据作法知,DE、FG分别是AB、AC的垂直平分线,
∴AM=BM,AN=CN,AP=BP=CP,
∴∠ABM=∠BAM,∠ACN=∠CAN,∠ABP=∠BAP,∠ACP=∠CAP,∠APD=∠APB,∠APF=∠APC,
∵∠MAN=50°,
∴∠ANM+∠AMN=180°﹣∠MAN=130°,
∵∠AMN=∠ABM+∠BAM,∠ANM=∠ACN+∠CAN,
∴∠BAM+∠CAN=65°,
∴∠BAC=65°+50°=115°,
∴∠ABP+∠ACP=∠BAC=115°,
∴∠BPC=360°﹣∠BAC﹣∠ABP﹣∠ACP=360°﹣115°﹣115°=130°,
∴∠MPN=∠APD+∠APF=×130°=65°,
故选:B.
【点睛】此题考查了线段垂直平分线的性质、等腰三角形的性质,熟记线段垂直平分线的性质、等腰三角形的性质是解题的关键.
8.(2024 山海关区一模)如图,在△ABC中,AB=AC,M为BC边上一点,且AM=AN,则∠BAM与∠NMC的关系一定成立的是( )
A.∠BAM=∠NMC B.∠BAM+∠NMC=∠BAC
C.∠BAM+∠NMC=∠B D.∠BAM=2∠NMC
【点拨】先证明∠B=∠C,∠AMN=∠ANM,再结合三角形的外角的性质进一步求解可得结论.
【解析】解:∵AB=AC,
∴∠B=∠C,
∵AM=AN,
∴∠AMN=∠ANM,
∴∠NMC+∠C=∠ANM,
∴∠NMC=∠AMN﹣∠B,
∵∠BAM+∠B=∠AMN+∠NMC,
∴∠BAM=∠AMN+∠NMC﹣∠B.
∴∠BAM=2∠NMC.
故选:D.
【点睛】本题考查的是等腰三角形的性质,三角形外角的性质,正确记忆修改知识点是解题关键.
9.(2024 花溪区一模)如图,在△ABC中,BC=7,∠ABC和∠ACB的平分线相交于点D,过点D作BC的平行线交AB于点E,交AC于点F,若△AEF的周长为14,则△ABC的周长是( )
A.14 B.19 C.21 D.23
【点拨】由角平分线的定义得到∠EBD=∠CBD,由平行线的性质得到∠EDB=∠DBC,因此∠EDB=∠EBD,推出ED=EB,同理:FD=FC,于是得到BE+CF=DE+DF=EF,由△AEF的周长=AE+AF+FE=AB+AC=14,即可求出△ABC的周长=AC+AB+BC=14+7=21.
【解析】解:∵BD平分∠ABC,
∴∠EBD=∠CBD,
∵EF//BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴ED=EB,
同理:FD=FC,
∴BE+CF=DE+DF=EF,
∵△AEF的周长=AE+AF+FE=AE+AF+BE+CF=AB+AC=14,
∴△ABC的周长=AC+AB+BC=14+7=21.
故选:C.
【点睛】本题考查等腰三角形的判定,平行线的性质,角平分线定义,关键是由平行线的性质,角平分线定义推出FE=BE+FC.
10.(2024 天津一模)已知等边三角形ABC的边长为3,D为BC边上的一点(点D不与点B,C重合),过D点作AB边的垂线,交AB于点G,用x表示线段AG的长度,y表示Rt△GBD的面积,有下列结论:①<x<3;②DB=x;③y=(3﹣x)2,其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
【点拨】①过点C作CE⊥AB于E,根据等边三角形的性质得AE=3/2,AE<AG<AB,据此可对结论①进行判断;
②根据AB=3,AG=x得GB=3﹣x,证∠GDB=30°,则DB=2GB=2(3﹣x),据此可对结论②进行判断;
③根据GB=3﹣x,DB=2(3﹣x),由勾股定理得DG=(3﹣x),然后根据三角形的面积求出y即可对结论③进行判断,综上所述即可得出答案.
【解析】解:①过点C作CE⊥AB于E,如图所示:
∵△ABC为等边三角形,且边长为3,
∴AB=3,AE=AB=,∠B=60°,
∵D为BC边上的一点(点D不与点B,C重合),DG⊥AB于G,
∴AE<AG<AB,
∴<x<3,
故结论①正确;
②∵AB=3,AG=x,
∴GB=AB﹣AG=3﹣x,
又∵∠B=60°,DG⊥AB于G,
∴∠GDB=30°,
∴DB=2GB=2(3﹣x),
故结论②不正确;
③在Rt△GBD中,GB=3﹣x,DB=2(3﹣x),
由勾股定理得:DG==(3﹣x),
∴y=GB DG==(3﹣x)2,
故结论③正确.
综上所述:正确的结论由①③,共2个.
故选:C.
【点睛】此题主要考查了等边三角形的性质,直角三角形的性质,三角形的面积,熟练掌握等边三角形的性质,直角三角形的性质,以及三角形的面积公式是解决问题的关键.
二.填空题
11.(2024 嘉善县一模)已知等腰三角形的两边长是4和8,则这个三角形的周长是 20 .
【点拨】分两种情况:当等腰三角形的腰长为4,底边长为8时;当等腰三角形的腰长为8,底边长为4时;然后分别进行计算即可解答.
【解析】解:分两种情况:
当等腰三角形的腰长为4,底边长为8时,
∵4+4=8,
∴不能组成三角形;
当等腰三角形的腰长为8,底边长为4时,
∴等腰三角形的周长=8+8+4=20;
综上所述:这个三角形的周长是20,
故答案为:20.
【点睛】本题考查了等腰三角形的性质,三角形的三边关系,分两种情况讨论是解题的关键.
12.(2024 贵州)如图,在△ABC中,以点A为圆心,线段AB的长为半径画弧,交BC于点D,连接AD.若AB=5,则AD的长为 5 .
【点拨】根据作一条线段等于已知线段的作法可得出AD=AB,即可求解.
【解析】解:由作图可知:AD=AB,
∵AB=5,
∴AD=5,
故答案为:5.
【点睛】本题考查了尺规作图,掌握作一条线段等于已知线段的方法是解题的关键.
13.(2024 镇江)如图,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC=8,CD=5,则BD= 3 .
【点拨】求出AD=8﹣5=3,由线段垂直平分线的性质推出BD=AD=3.
【解析】解:∵AC=8,CD=5,
∴AD=8﹣5=3,
∵D在AB的垂直平分线上,
∴BD=AD=3.
故答案为:3.
【点睛】本题考查线段垂直平分线的性质,关键是由线段垂直平分线的性质推出BD=AD.
14.(2024 钱塘区三模)如图,△ABC为等边三角形,点D为BC延长线上一点.若,∠CAD=15°,则AB的长为 2 .
【点拨】过点A作AE⊥BC于点E,由等边三角形的性质得出BE=CE,∠BAE=∠CAE,∠BAC=60°,AB=AC,即可证得∠EAD=45°,得出△AED是等腰直角三角形,设CE=x,根据勾股定理即可求出AE的长,在Rt△AED中根据勾股定理即可求出x的值,从而得出AB的长.
【解析】解:过点A作AE⊥BC于点E,
∵△ABC是等边三角形,
∴BE=CE,∠BAE=∠CAE,∠BAC=60°,AB=AC,
∴∠BAE=∠CAE=30°,
∵∠CAD=15°,
∴∠EAD=∠CAE+∠CAD=30°+15°=45°,
∴△AED是等腰直角三角形,
设CE=x,
∵∠CAE=30°,AE⊥BC,
∴AC=2CE=2x,
由勾股定理得,AE=,
∴DE=AE=,
由勾股定理得,AE2+DE2=AD2,
∴,
解得x=1,
∴AC=2x=2,
∴AB=AC=2,
故答案为:2.
【点睛】本题了等边三角形的性质,勾股定理,等腰三角形的判定与性质,直角三角形的性质,熟练掌握等边三角形的性质是解题的关键.
15.(2024 蒙阴县二模)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 80° .
【点拨】由等腰三角形的性质可得∠O=∠CDO,∠DCE=∠DEC,由外角性质可得∠O=25°,即可求解.
【解析】解:∵OC=CD=DE,
∴∠O=∠CDO,∠DCE=∠DEC,
∵∠DCE=∠O+∠CDO=2∠O,
∴∠DEC=2∠O,
∴∠BDE=∠O+∠DEC=3∠O=75°,
∴∠O=25°,
∴∠DCE=∠DEC=50°,
∴∠CDE=80°,
故答案为:80°.
【点睛】本题考查了等腰三角形的性质,三角形内角和定理,熟练运用这些性质进行推理是本题关键.
16.(2024 萧县二模)如图,D,E,F是△ABC的边BC,AB,AC上的点,且满足DB=DE,DC=DF,DC=DF,∠BDF=∠CDE=135°,连接BF,CE,过点C作CH⊥AB,垂足为H.
(1)∠A的度数是 45° .
(2)若AH=5,AF=4,则EH= 1 .
【点拨】(1)先根据邻补角定义及∠CDE=135°得∠CDF=45°,再根据等腰三角形性质及三角形内角和定理得∠DBE=67.5°,同理∠DCF=67.5°,由此可得∠A的度数;
(2)在AB上截取AG=AF=4,连接CG,则GH=AH﹣AG=1,证△BDF和△EDC全等得BF=CE,再证△ACG和△ABF全等得CG=BF,从而得CG=CE,然后根据等腰三角形的性质可得EH的长.
【解析】解:(1)∵∠CDE+∠BDE=180°,∠CDE=135°,
∴∠CDF=180°﹣∠BDF=45°,
∵DB=DE,
∴∠DBE=∠DEB=(180°﹣∠BDE)=×(180°﹣45°)=67.5°,
同理:∠DCF=67.5°,
∴∠A=180°﹣(∠DBE+∠DCF)=180°﹣(67.5°+67.5°)=45°,
故答案为:45°.
(2)在AB上截取AG=AF=4,连接CG,如图所示:
∵AH=5,
∴GH=AH﹣AG=5﹣4=1,
在△BDF和△EDC中,
,
∴△BDF≌△EDC(SAS),
∴BF=CE,
由(1)可知:∠DCF=67.5°,∠DBE=67.5°,
∴∠DCF=∠DBE,
即∠ACB=∠ABC,
∴AC=AB,
在△ACG和△ABF中,
,
∴△ACG≌△ABF
∴CG=BF,
∴CG=CE,
∵CH⊥AB,
∴EH=GH=1.
【点睛】此题主要考查了等腰三角形的性质,全等三角形的判定和性质,熟练掌握等腰三角形的性质,全等三角形的判定和性质是解决问题的关键,正确地作出辅助线构造全等三角形和等腰三角形是解决问题的难点.
三.解答题
17.(2024 濠江区一模)如图,点C为∠AOB平分线上一点,CD∥OB交OA于点D.求证:△DOC是等腰三角形.
【点拨】根据平行线的性质、角平分线的性质证明∠AOC=∠DCO,由等腰三角形的判定即可求解.
【解析】证明:∵OC平分∠AOB,
∴∠AOC=∠BOC.
∵CD∥OB,
∴∠DCO=∠BOC,
∴∠AOC=∠DCO,
∴OD=CD,
∴△DOC是等腰三角形.
【点睛】此题主要考查等腰三角形的判定,平行线的性质,解题的关键是正确推理.
18.(2024 镇海区校级一模)如图,在△ABC中,D、E分别是△ABC边AB、AC上的点,已知DE∥BC且DB=DE.
(1)求证:BE是△ABC的角平分线;
(2)若∠A=65°,∠C=45°,求∠AEB的度数.
【点拨】(1)根据DE∥BC证得∠DEB=∠CBE,根据DB=DE证得∠DBE=∠DEB,等量代换证得∠CBE=∠DBE,进而证得结论;
(2)根据∠A=65°,∠C=45°求出∠ABC=70°,所以∠ABE=35°,再利用三角形内角和求出∠AEB的度数.
【解析】(1)证明:∵DE∥BC,
∴∠DEB=∠CBE,
∵DB=DE,
∴∠DBE=∠DEB,
∴∠CBE=∠DBE,
∴BE是△ABC的角平分线;
(2)解:∵∠A=65°,∠C=45°,
∴∠ABC=70°,
∵BE是△ABC的角平分线,
∴∠ABE=35°,
∴∠AEB=180°﹣∠A﹣∠ABE=80°.
【点睛】本题考查了平行线的性质以及等腰三角形的判定和性质,解题的关键是熟练掌握相关的性质定理.
19.(2024 利川市校级模拟)如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
(2)求∠BQM的大小.
【点拨】(1)根据等边三角形的性质求得∠BAC=∠BCA=60°,再根据等边三角形的边长相等求得CM=AN,最后由SAS证明全等即可;
(2)根据全等三角形的性质:对应角相等,求得∠CAM=∠ABN;然后由∠BQM=∠ABN+∠BAQ来找∠BAC与其的关系.
【解析】解:(1)∵△ABC为等边三角形,
∴AB=BC=CA,∠BAC=∠BCA=60°,
∵BM=CN,
∴CM=AN,
又∵∠BAN=∠ACM,
∴△BAN≌△ACM;
(2)∴∠CAM=∠ABN,
∴∠BQM=∠ABN+∠BAQ=∠CAM+∠BAQ=∠BAC=60°.
【点睛】本题主要考查了全等三角形的判定与性质.利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键.在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便.
20.(2024 越秀区校级一模)如图,已知点D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F,连接AD,若AD垂直平分EF,求证:AD是△ABC的角平分线.
【点拨】根据线段垂直平分线的性质得到DE=DF,再根据角平分线的判定定理即可证得AD是△ABC的角平分线.
【解析】证明:∵AD垂直平分EF,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
【点睛】本题考查了角平分线判定定理,线段垂直平分线性质;熟记“线段垂直平分线上的点到线段两端的距离相等”和“到角两边距离相等的点都在角的平分线上”是解决问题的关键.
21.(2024 龙亭区校级一模)如图,在四边形ABCD中,AB=AD,CB=CD,∠A=60°,点E为AD上一点,连接BD,CE交于点F,CE∥AB.
(1)判断△DEF的形状,并说明理由;
(2)若AD=12,CE=7,则CF的长为 2 .
【点拨】(1)先证明△ABD为等边三角形,进而得到∠ADB=60°,结合平行线的性质,推出△DEF是等边三角形即可;
(2)连接AC交BD于点O,易得AC垂直平分BD,三线合一,结合平行线的性质,推出CE=AE,进而求出DE的长,等边三角形的性质,得到EF的长,利用CE﹣EF求出CF的长即可.
【解析】解:(1)△DEF是等边三角形,理由如下:
∵AB=AD,∠A=60°,
∴△ABD为等边三角形,
∴∠ADB=60°,∠ABD=60°,
∵CE∥AB,
∴∠DEF=∠A=60°,∠EFD=∠ABD=60°,
∴△DEF是等边三角形;
(2)连接AC交BD于点O,如图,
∵AB=AD,CB=CD,
∴AC垂直平分BD,
∴AO⊥BD,
∴∠BAO=∠DAO=30°,
∵CE∥AB,
∴∠ACE=∠BAO=∠DAO,
∴AE=CE=7,
∴DE=AD﹣AE=12﹣7=5,
∵△DEF是等边三角形,
∴EF=DE=5,
∴CF=CE﹣EF=2;
故答案为:2.
【点睛】本题考查等边三角形的判定与性质,线段垂直平分线的性质,等腰三角形的判定与性质,证明AE=CE是解题的关键.
22.(2024 路南区二模)等边△ABC的边长为2,P为△ABC内一点,连接BP,PC,延长PC到点D,使CD=PC.
(1)如图1,延长BC到点E,使CE=BC,连接AE,DE.
①求证:BP∥DE;
②若BP⊥AC,求∠AED的度数;
(2)如图2,连接AD,若BP⊥AD,BP=1,则AD= .
【点拨】(1)①证明△DEC和△PBC全等得∠DEC=∠PBC,再根据平行线的判定可得出结论;
②延长AC交ED的延长线于F,根据等边三角形性质得BC=AC,∠ACB=60°,进而可求出∠CAE=∠CEA=30°,再由①BP∥DE,BP⊥AC得DE⊥AC,由此得∠CED=30°,据此可得∠AED的度数;
(2)延长BC到E是CE=BC,连接AE,DE,先求出∠BAE=90°,BE=4,由勾股定理得AE=,根据△DEC≌△PBC得BP=DE=1,再根据BP⊥AD,BP∥DE得DE⊥AD,然后由勾股定理即可求出AD的长.
【解析】(1)①证明:在△DEC和△PBC中,
,
∴△DEC≌△PBC(SAS),
∴∠DEC=∠PBC,
∴BP∥DE;
②解:延长AC交ED的延长线于F,如图1所示:
∵△ABC为等边三角形,
∴BC=AC,∠ACB=60°,
又∵CE=BC,
∴AC=CE,
∴∠CAE=∠CEA,
∵∠CAE+∠CEA=∠ACB=60°,
∴∠CAE=∠CEA=30°,
由①可知:BP∥DE,
∵BP⊥AC,
∴DE⊥AC,即∠F=90°,
又∵∠ECF=∠ACB=60°,
∴∠CED=90°﹣∠ECF=30°,
∴∠AED=∠CEA+∠CED=30°+30°=60°;
(2)延长BC到E是CE=BC,连接AE,DE,如图2所示:
由(1)②可知:∠CAE=30°,
∵△ABC为等边三角形,且边长为2,
∴AB=BC=AC=CE=2,∠BAC=60°,
∴∠BAE=∠BAC+∠CAE=90°,BE=BC+CE=4,
在Rt△ABE中,由勾股定理得:AE==,
由(1)①可知:△DEC≌△PBC,
∴BP=DE=1,
又∵BP⊥AD,BP∥DE,
∴DE⊥AD,
在Rt△ADE中,由勾股定理得:AD==.
故答案为:.
【点睛】此题主要考查了等边三角形的性质,全等三角形的判定和性质,勾股定理,理解等边三角形的性质,熟练掌握全等三角形的判定和性质,灵活运用勾股定理进行计算是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题18 等腰三角形
一.选择题
1.(2024 宿迁二模)等腰三角形的一个内角为80°,则这个等腰三角形的底角为( )
A.80°或50° B.80° C.50° D.50°或20°
2.(2024 兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB=( )
A.100° B.115° C.130° D.145°
3.(2024 大荔县校级二模)如图,在△ABC中,点D是BC上一点.连接AD,已知AB=5,∠B=70°,∠C=35°,若∠BAD=40°,则CD的长为( )
A.4 B.5 C.6 D.7
4.(2024 邯山区校级四模)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD的夹角为( )
A.10° B.15° C.20° D.30°
5.(2024 黄岩区一模)如图,△ABC是等腰三角形,AB=AC,∠BAC是钝角.点D在底边BC上,连接AD,恰好把△ABC分割成两个等腰三角形,则∠B的度数是( )
A.30° B.36° C.45° D.60°
6.(2024 自贡)如图,等边△ABC钢架的立柱CD⊥AB于点D,AB长12m.现将钢架立柱缩短成DE,∠BED=60°.则新钢架减少用钢( )
A.(24﹣12)m B.(24﹣8)m C.(24﹣6)m D.(24﹣4)m
7.(2024 海宁市校级模拟)如图所示的△ABC,进行以下操作:①以A,B为圆心,大于AB为半径作圆弧,相交点D,E;②以A,C为圆心,大于AC为半径作圆弧,相交于点F,G.两直线DE,FG相交于△ABC外一点P,且分别交BC点M,N.若∠MAN=50°,则∠MPN等于( )
A.60° B.65° C.70° D.75°
8.(2024 山海关区一模)如图,在△ABC中,AB=AC,M为BC边上一点,且AM=AN,则∠BAM与∠NMC的关系一定成立的是( )
A.∠BAM=∠NMC B.∠BAM+∠NMC=∠BAC
C.∠BAM+∠NMC=∠B D.∠BAM=2∠NMC
9.(2024 花溪区一模)如图,在△ABC中,BC=7,∠ABC和∠ACB的平分线相交于点D,过点D作BC的平行线交AB于点E,交AC于点F,若△AEF的周长为14,则△ABC的周长是( )
A.14 B.19 C.21 D.23
10.(2024 天津一模)已知等边三角形ABC的边长为3,D为BC边上的一点(点D不与点B,C重合),过D点作AB边的垂线,交AB于点G,用x表示线段AG的长度,y表示Rt△GBD的面积,有下列结论:①<x<3;②DB=x;③y=(3﹣x)2,其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
二.填空题
11.(2024 嘉善县一模)已知等腰三角形的两边长是4和8,则这个三角形的周长是 .
12.(2024 贵州)如图,在△ABC中,以点A为圆心,线段AB的长为半径画弧,交BC于点D,连接AD.若AB=5,则AD的长为 .
13.(2024 镇江)如图,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC=8,CD=5,则BD= .
14.(2024 钱塘区三模)如图,△ABC为等边三角形,点D为BC延长线上一点.若,∠CAD=15°,则AB的长为 .
15.(2024 蒙阴县二模)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 .
16.(2024 萧县二模)如图,D,E,F是△ABC的边BC,AB,AC上的点,且满足DB=DE,DC=DF,DC=DF,∠BDF=∠CDE=135°,连接BF,CE,过点C作CH⊥AB,垂足为H.
(1)∠A的度数是 .
(2)若AH=5,AF=4,则EH= .
三.解答题
17.(2024 濠江区一模)如图,点C为∠AOB平分线上一点,CD∥OB交OA于点D.求证:△DOC是等腰三角形.
18.(2024 镇海区校级一模)如图,在△ABC中,D、E分别是△ABC边AB、AC上的点,已知DE∥BC且DB=DE.
(1)求证:BE是△ABC的角平分线;
(2)若∠A=65°,∠C=45°,求∠AEB的度数.
19.(2024 利川市校级模拟)如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
(2)求∠BQM的大小.
20.(2024 越秀区校级一模)如图,已知点D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F,连接AD,若AD垂直平分EF,求证:AD是△ABC的角平分线.
21.(2024 龙亭区校级一模)如图,在四边形ABCD中,AB=AD,CB=CD,∠A=60°,点E为AD上一点,连接BD,CE交于点F,CE∥AB.
(1)判断△DEF的形状,并说明理由;
(2)若AD=12,CE=7,则CF的长为 .
22.(2024 路南区二模)等边△ABC的边长为2,P为△ABC内一点,连接BP,PC,延长PC到点D,使CD=PC.
(1)如图1,延长BC到点E,使CE=BC,连接AE,DE.
①求证:BP∥DE;
②若BP⊥AC,求∠AED的度数;
(2)如图2,连接AD,若BP⊥AD,BP=1,则AD= .
答案与解析
一.选择题
1.(2024 宿迁二模)等腰三角形的一个内角为80°,则这个等腰三角形的底角为( )
A.80°或50° B.80° C.50° D.50°或20°
【点拨】由于不明确80°的角是等腰三角形的底角还是顶角,故应分80°的角是顶角和底角两种情况讨论.
【解析】解:分两种情况:
①当80°的角为等腰三角形的顶角时,
底角的度数=(180°﹣80°)÷2=50°;
②当80°的角为等腰三角形的底角时,其底角为80°,
故它的底角度数是50°或80°.
故选:A.
【点睛】本题考查的是等腰三角形的性质及三角形内角和定理;解答此题时要注意80°的角是顶角和底角两种情况,不要漏解,分类讨论是正确解答本题的关键.
2.(2024 兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB=( )
A.100° B.115° C.130° D.145°
【点拨】根据等边对等角得出∠B=∠C,根据∠BAC=130°即可求出∠C的度数,由DA⊥AC得出∠DAC=90°,从而求出∠ADC的度数,问题得解.
【解析】解:在△ABC中,AB=AC,
∴∠B=∠C,
∵∠BAC=130°,
∴∠B=∠C==25°,
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90°﹣25°=65°,
∴∠ADB=180°﹣∠ADC=180°﹣65°=115°,
故选:B.
【点睛】本题考查了等腰三角形的性质,三角形内角和定理,熟练掌握这些知识点是解题的关键.
3.(2024 大荔县校级二模)如图,在△ABC中,点D是BC上一点.连接AD,已知AB=5,∠B=70°,∠C=35°,若∠BAD=40°,则CD的长为( )
A.4 B.5 C.6 D.7
【点拨】根据三角形的面积好多了,等腰三角形的判定和性质定理,以及三角形外角的性质即可得到结论.
【解析】解:∵∠B=70°,∠BAD=40°,
∴∠ADB=180°﹣∠B﹣∠BAD=70°,
∴AD=AB=5,
∵∠ADB=∠CAD+∠C,
∴∠CAD=∠ADB﹣∠C=35°,
∴∠CAD=∠C,
∴CD=AD=5,
故选:B.
【点睛】本题考查了等腰三角形的判定和性质,三角形外角的性质,熟练掌握等腰三角形的判定和性质定理是解题的关键.
4.(2024 邯山区校级四模)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD的夹角为( )
A.10° B.15° C.20° D.30°
【点拨】延长AD与BC交于点E,根据等边三角形和等腰直角三角形性质得∠ABC=∠BAC=60°,∠CAD=45°,进而得∠BAD=105°,然后根据三角形内角和定理求出∠E即可.
【解析】解:延长AD与BC交于点E,如图所示:
∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
又∵△ACD为等腰直角三角形,AC=CD,
∴∠CAD=45°,
∴∠BAD=∠BAC+∠CAD=60°+45°=105°,
∴∠E=180°﹣(∠ABC+∠BAD)=180°﹣(60°+105°)=15°.
即直线BC与直线AD的夹角为15°.
故选:B.
【点睛】此题主要考查了据等边三角形和等腰直角三角形性质,三角形的内角和定理,熟练掌握等边三角形和等腰直角三角形性质,三角形的内角和定理是解决问题的关键.
5.(2024 黄岩区一模)如图,△ABC是等腰三角形,AB=AC,∠BAC是钝角.点D在底边BC上,连接AD,恰好把△ABC分割成两个等腰三角形,则∠B的度数是( )
A.30° B.36° C.45° D.60°
【点拨】由等腰三角形的性质得出∠B=∠C=∠BAD,∠ADC=∠DAC,根据三角形外角的性质得∠ADC=∠DAC=∠B+∠BAD=2∠B=2∠C,设∠C=x,在△ADC中,由三角形内角和定理得出方程,解方程即可.
【解析】解:∵AB=AC,AD,恰好把△ABC分割成两个等腰三角形,
∴∠B=∠C,∠B=∠BAD,∠ADC=∠DAC,
∵∠ADC=∠B+∠BAD,
∴∠ADC=∠DAC=∠B+∠BAD=2∠B=2∠C,
设∠C=x,
在△ADC中,∠CAD+∠ADC+∠C=180°,
即x+2x+2x=180°,
解得:x=36°,
∴∠C=36°,
∴∠B=36°,
故选:B.
【点睛】本题考查了等腰三角形的性质、三角形内角和定理、三角形的外角性质等知识,解题的关键是理解题意,学会利用方程去思考问题.
6.(2024 自贡)如图,等边△ABC钢架的立柱CD⊥AB于点D,AB长12m.现将钢架立柱缩短成DE,∠BED=60°.则新钢架减少用钢( )
A.(24﹣12)m B.(24﹣8)m C.(24﹣6)m D.(24﹣4)m
【点拨】根据特殊直角三角形求出DE,CD和BE的长,从而得出减少用钢的长度.
【解析】解:∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC=AC=12,BD=6,
∴CD=,
∵∠BED=60°,
∴DE=,BE=AE=,
∴减少用钢为(AB+AC+BC+CD)﹣(AE+BE+AB+DE)=AC+BC+CD﹣AE﹣BE﹣DE=24﹣(cm),
故选:D.
【点睛】本题考查了等边三角形的性质,特殊直角三角形的三边关系,掌握特殊角的三边关系是解题的关键.
7.(2024 海宁市校级模拟)如图所示的△ABC,进行以下操作:①以A,B为圆心,大于AB为半径作圆弧,相交点D,E;②以A,C为圆心,大于AC为半径作圆弧,相交于点F,G.两直线DE,FG相交于△ABC外一点P,且分别交BC点M,N.若∠MAN=50°,则∠MPN等于( )
A.60° B.65° C.70° D.75°
【点拨】根据作法知,DE、FG分别是AB、AC的垂直平分线,根据线段垂直平分线的性质得出AM=BM,AN=CN,AP=BP=CP,根据等腰三角形的性质得出∠ABM=∠BAM,∠ACN=∠CAN,∠ABP=∠BAP,∠ACP=∠CAP,∠APD=∠APB,∠APF=∠APC,根据三角形内角和定理求出∠ANM+∠AMN=130°,根据三角形外角性质及角的和差求出∠BAC=115°,根据四边形内角和定理求出∠BPC=130°,再根据∠MPN=∠APD+∠APF求解即可.
【解析】解:如图,连接AP、BP、CP,
根据作法知,DE、FG分别是AB、AC的垂直平分线,
∴AM=BM,AN=CN,AP=BP=CP,
∴∠ABM=∠BAM,∠ACN=∠CAN,∠ABP=∠BAP,∠ACP=∠CAP,∠APD=∠APB,∠APF=∠APC,
∵∠MAN=50°,
∴∠ANM+∠AMN=180°﹣∠MAN=130°,
∵∠AMN=∠ABM+∠BAM,∠ANM=∠ACN+∠CAN,
∴∠BAM+∠CAN=65°,
∴∠BAC=65°+50°=115°,
∴∠ABP+∠ACP=∠BAC=115°,
∴∠BPC=360°﹣∠BAC﹣∠ABP﹣∠ACP=360°﹣115°﹣115°=130°,
∴∠MPN=∠APD+∠APF=×130°=65°,
故选:B.
【点睛】此题考查了线段垂直平分线的性质、等腰三角形的性质,熟记线段垂直平分线的性质、等腰三角形的性质是解题的关键.
8.(2024 山海关区一模)如图,在△ABC中,AB=AC,M为BC边上一点,且AM=AN,则∠BAM与∠NMC的关系一定成立的是( )
A.∠BAM=∠NMC B.∠BAM+∠NMC=∠BAC
C.∠BAM+∠NMC=∠B D.∠BAM=2∠NMC
【点拨】先证明∠B=∠C,∠AMN=∠ANM,再结合三角形的外角的性质进一步求解可得结论.
【解析】解:∵AB=AC,
∴∠B=∠C,
∵AM=AN,
∴∠AMN=∠ANM,
∴∠NMC+∠C=∠ANM,
∴∠NMC=∠AMN﹣∠B,
∵∠BAM+∠B=∠AMN+∠NMC,
∴∠BAM=∠AMN+∠NMC﹣∠B.
∴∠BAM=2∠NMC.
故选:D.
【点睛】本题考查的是等腰三角形的性质,三角形外角的性质,正确记忆修改知识点是解题关键.
9.(2024 花溪区一模)如图,在△ABC中,BC=7,∠ABC和∠ACB的平分线相交于点D,过点D作BC的平行线交AB于点E,交AC于点F,若△AEF的周长为14,则△ABC的周长是( )
A.14 B.19 C.21 D.23
【点拨】由角平分线的定义得到∠EBD=∠CBD,由平行线的性质得到∠EDB=∠DBC,因此∠EDB=∠EBD,推出ED=EB,同理:FD=FC,于是得到BE+CF=DE+DF=EF,由△AEF的周长=AE+AF+FE=AB+AC=14,即可求出△ABC的周长=AC+AB+BC=14+7=21.
【解析】解:∵BD平分∠ABC,
∴∠EBD=∠CBD,
∵EF//BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴ED=EB,
同理:FD=FC,
∴BE+CF=DE+DF=EF,
∵△AEF的周长=AE+AF+FE=AE+AF+BE+CF=AB+AC=14,
∴△ABC的周长=AC+AB+BC=14+7=21.
故选:C.
【点睛】本题考查等腰三角形的判定,平行线的性质,角平分线定义,关键是由平行线的性质,角平分线定义推出FE=BE+FC.
10.(2024 天津一模)已知等边三角形ABC的边长为3,D为BC边上的一点(点D不与点B,C重合),过D点作AB边的垂线,交AB于点G,用x表示线段AG的长度,y表示Rt△GBD的面积,有下列结论:①<x<3;②DB=x;③y=(3﹣x)2,其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
【点拨】①过点C作CE⊥AB于E,根据等边三角形的性质得AE=3/2,AE<AG<AB,据此可对结论①进行判断;
②根据AB=3,AG=x得GB=3﹣x,证∠GDB=30°,则DB=2GB=2(3﹣x),据此可对结论②进行判断;
③根据GB=3﹣x,DB=2(3﹣x),由勾股定理得DG=(3﹣x),然后根据三角形的面积求出y即可对结论③进行判断,综上所述即可得出答案.
【解析】解:①过点C作CE⊥AB于E,如图所示:
∵△ABC为等边三角形,且边长为3,
∴AB=3,AE=AB=,∠B=60°,
∵D为BC边上的一点(点D不与点B,C重合),DG⊥AB于G,
∴AE<AG<AB,
∴<x<3,
故结论①正确;
②∵AB=3,AG=x,
∴GB=AB﹣AG=3﹣x,
又∵∠B=60°,DG⊥AB于G,
∴∠GDB=30°,
∴DB=2GB=2(3﹣x),
故结论②不正确;
③在Rt△GBD中,GB=3﹣x,DB=2(3﹣x),
由勾股定理得:DG==(3﹣x),
∴y=GB DG==(3﹣x)2,
故结论③正确.
综上所述:正确的结论由①③,共2个.
故选:C.
【点睛】此题主要考查了等边三角形的性质,直角三角形的性质,三角形的面积,熟练掌握等边三角形的性质,直角三角形的性质,以及三角形的面积公式是解决问题的关键.
二.填空题
11.(2024 嘉善县一模)已知等腰三角形的两边长是4和8,则这个三角形的周长是 20 .
【点拨】分两种情况:当等腰三角形的腰长为4,底边长为8时;当等腰三角形的腰长为8,底边长为4时;然后分别进行计算即可解答.
【解析】解:分两种情况:
当等腰三角形的腰长为4,底边长为8时,
∵4+4=8,
∴不能组成三角形;
当等腰三角形的腰长为8,底边长为4时,
∴等腰三角形的周长=8+8+4=20;
综上所述:这个三角形的周长是20,
故答案为:20.
【点睛】本题考查了等腰三角形的性质,三角形的三边关系,分两种情况讨论是解题的关键.
12.(2024 贵州)如图,在△ABC中,以点A为圆心,线段AB的长为半径画弧,交BC于点D,连接AD.若AB=5,则AD的长为 5 .
【点拨】根据作一条线段等于已知线段的作法可得出AD=AB,即可求解.
【解析】解:由作图可知:AD=AB,
∵AB=5,
∴AD=5,
故答案为:5.
【点睛】本题考查了尺规作图,掌握作一条线段等于已知线段的方法是解题的关键.
13.(2024 镇江)如图,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC=8,CD=5,则BD= 3 .
【点拨】求出AD=8﹣5=3,由线段垂直平分线的性质推出BD=AD=3.
【解析】解:∵AC=8,CD=5,
∴AD=8﹣5=3,
∵D在AB的垂直平分线上,
∴BD=AD=3.
故答案为:3.
【点睛】本题考查线段垂直平分线的性质,关键是由线段垂直平分线的性质推出BD=AD.
14.(2024 钱塘区三模)如图,△ABC为等边三角形,点D为BC延长线上一点.若,∠CAD=15°,则AB的长为 2 .
【点拨】过点A作AE⊥BC于点E,由等边三角形的性质得出BE=CE,∠BAE=∠CAE,∠BAC=60°,AB=AC,即可证得∠EAD=45°,得出△AED是等腰直角三角形,设CE=x,根据勾股定理即可求出AE的长,在Rt△AED中根据勾股定理即可求出x的值,从而得出AB的长.
【解析】解:过点A作AE⊥BC于点E,
∵△ABC是等边三角形,
∴BE=CE,∠BAE=∠CAE,∠BAC=60°,AB=AC,
∴∠BAE=∠CAE=30°,
∵∠CAD=15°,
∴∠EAD=∠CAE+∠CAD=30°+15°=45°,
∴△AED是等腰直角三角形,
设CE=x,
∵∠CAE=30°,AE⊥BC,
∴AC=2CE=2x,
由勾股定理得,AE=,
∴DE=AE=,
由勾股定理得,AE2+DE2=AD2,
∴,
解得x=1,
∴AC=2x=2,
∴AB=AC=2,
故答案为:2.
【点睛】本题了等边三角形的性质,勾股定理,等腰三角形的判定与性质,直角三角形的性质,熟练掌握等边三角形的性质是解题的关键.
15.(2024 蒙阴县二模)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是 80° .
【点拨】由等腰三角形的性质可得∠O=∠CDO,∠DCE=∠DEC,由外角性质可得∠O=25°,即可求解.
【解析】解:∵OC=CD=DE,
∴∠O=∠CDO,∠DCE=∠DEC,
∵∠DCE=∠O+∠CDO=2∠O,
∴∠DEC=2∠O,
∴∠BDE=∠O+∠DEC=3∠O=75°,
∴∠O=25°,
∴∠DCE=∠DEC=50°,
∴∠CDE=80°,
故答案为:80°.
【点睛】本题考查了等腰三角形的性质,三角形内角和定理,熟练运用这些性质进行推理是本题关键.
16.(2024 萧县二模)如图,D,E,F是△ABC的边BC,AB,AC上的点,且满足DB=DE,DC=DF,DC=DF,∠BDF=∠CDE=135°,连接BF,CE,过点C作CH⊥AB,垂足为H.
(1)∠A的度数是 45° .
(2)若AH=5,AF=4,则EH= 1 .
【点拨】(1)先根据邻补角定义及∠CDE=135°得∠CDF=45°,再根据等腰三角形性质及三角形内角和定理得∠DBE=67.5°,同理∠DCF=67.5°,由此可得∠A的度数;
(2)在AB上截取AG=AF=4,连接CG,则GH=AH﹣AG=1,证△BDF和△EDC全等得BF=CE,再证△ACG和△ABF全等得CG=BF,从而得CG=CE,然后根据等腰三角形的性质可得EH的长.
【解析】解:(1)∵∠CDE+∠BDE=180°,∠CDE=135°,
∴∠CDF=180°﹣∠BDF=45°,
∵DB=DE,
∴∠DBE=∠DEB=(180°﹣∠BDE)=×(180°﹣45°)=67.5°,
同理:∠DCF=67.5°,
∴∠A=180°﹣(∠DBE+∠DCF)=180°﹣(67.5°+67.5°)=45°,
故答案为:45°.
(2)在AB上截取AG=AF=4,连接CG,如图所示:
∵AH=5,
∴GH=AH﹣AG=5﹣4=1,
在△BDF和△EDC中,
,
∴△BDF≌△EDC(SAS),
∴BF=CE,
由(1)可知:∠DCF=67.5°,∠DBE=67.5°,
∴∠DCF=∠DBE,
即∠ACB=∠ABC,
∴AC=AB,
在△ACG和△ABF中,
,
∴△ACG≌△ABF
∴CG=BF,
∴CG=CE,
∵CH⊥AB,
∴EH=GH=1.
【点睛】此题主要考查了等腰三角形的性质,全等三角形的判定和性质,熟练掌握等腰三角形的性质,全等三角形的判定和性质是解决问题的关键,正确地作出辅助线构造全等三角形和等腰三角形是解决问题的难点.
三.解答题
17.(2024 濠江区一模)如图,点C为∠AOB平分线上一点,CD∥OB交OA于点D.求证:△DOC是等腰三角形.
【点拨】根据平行线的性质、角平分线的性质证明∠AOC=∠DCO,由等腰三角形的判定即可求解.
【解析】证明:∵OC平分∠AOB,
∴∠AOC=∠BOC.
∵CD∥OB,
∴∠DCO=∠BOC,
∴∠AOC=∠DCO,
∴OD=CD,
∴△DOC是等腰三角形.
【点睛】此题主要考查等腰三角形的判定,平行线的性质,解题的关键是正确推理.
18.(2024 镇海区校级一模)如图,在△ABC中,D、E分别是△ABC边AB、AC上的点,已知DE∥BC且DB=DE.
(1)求证:BE是△ABC的角平分线;
(2)若∠A=65°,∠C=45°,求∠AEB的度数.
【点拨】(1)根据DE∥BC证得∠DEB=∠CBE,根据DB=DE证得∠DBE=∠DEB,等量代换证得∠CBE=∠DBE,进而证得结论;
(2)根据∠A=65°,∠C=45°求出∠ABC=70°,所以∠ABE=35°,再利用三角形内角和求出∠AEB的度数.
【解析】(1)证明:∵DE∥BC,
∴∠DEB=∠CBE,
∵DB=DE,
∴∠DBE=∠DEB,
∴∠CBE=∠DBE,
∴BE是△ABC的角平分线;
(2)解:∵∠A=65°,∠C=45°,
∴∠ABC=70°,
∵BE是△ABC的角平分线,
∴∠ABE=35°,
∴∠AEB=180°﹣∠A﹣∠ABE=80°.
【点睛】本题考查了平行线的性质以及等腰三角形的判定和性质,解题的关键是熟练掌握相关的性质定理.
19.(2024 利川市校级模拟)如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
(2)求∠BQM的大小.
【点拨】(1)根据等边三角形的性质求得∠BAC=∠BCA=60°,再根据等边三角形的边长相等求得CM=AN,最后由SAS证明全等即可;
(2)根据全等三角形的性质:对应角相等,求得∠CAM=∠ABN;然后由∠BQM=∠ABN+∠BAQ来找∠BAC与其的关系.
【解析】解:(1)∵△ABC为等边三角形,
∴AB=BC=CA,∠BAC=∠BCA=60°,
∵BM=CN,
∴CM=AN,
又∵∠BAN=∠ACM,
∴△BAN≌△ACM;
(2)∴∠CAM=∠ABN,
∴∠BQM=∠ABN+∠BAQ=∠CAM+∠BAQ=∠BAC=60°.
【点睛】本题主要考查了全等三角形的判定与性质.利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键.在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便.
20.(2024 越秀区校级一模)如图,已知点D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F,连接AD,若AD垂直平分EF,求证:AD是△ABC的角平分线.
【点拨】根据线段垂直平分线的性质得到DE=DF,再根据角平分线的判定定理即可证得AD是△ABC的角平分线.
【解析】证明:∵AD垂直平分EF,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
【点睛】本题考查了角平分线判定定理,线段垂直平分线性质;熟记“线段垂直平分线上的点到线段两端的距离相等”和“到角两边距离相等的点都在角的平分线上”是解决问题的关键.
21.(2024 龙亭区校级一模)如图,在四边形ABCD中,AB=AD,CB=CD,∠A=60°,点E为AD上一点,连接BD,CE交于点F,CE∥AB.
(1)判断△DEF的形状,并说明理由;
(2)若AD=12,CE=7,则CF的长为 2 .
【点拨】(1)先证明△ABD为等边三角形,进而得到∠ADB=60°,结合平行线的性质,推出△DEF是等边三角形即可;
(2)连接AC交BD于点O,易得AC垂直平分BD,三线合一,结合平行线的性质,推出CE=AE,进而求出DE的长,等边三角形的性质,得到EF的长,利用CE﹣EF求出CF的长即可.
【解析】解:(1)△DEF是等边三角形,理由如下:
∵AB=AD,∠A=60°,
∴△ABD为等边三角形,
∴∠ADB=60°,∠ABD=60°,
∵CE∥AB,
∴∠DEF=∠A=60°,∠EFD=∠ABD=60°,
∴△DEF是等边三角形;
(2)连接AC交BD于点O,如图,
∵AB=AD,CB=CD,
∴AC垂直平分BD,
∴AO⊥BD,
∴∠BAO=∠DAO=30°,
∵CE∥AB,
∴∠ACE=∠BAO=∠DAO,
∴AE=CE=7,
∴DE=AD﹣AE=12﹣7=5,
∵△DEF是等边三角形,
∴EF=DE=5,
∴CF=CE﹣EF=2;
故答案为:2.
【点睛】本题考查等边三角形的判定与性质,线段垂直平分线的性质,等腰三角形的判定与性质,证明AE=CE是解题的关键.
22.(2024 路南区二模)等边△ABC的边长为2,P为△ABC内一点,连接BP,PC,延长PC到点D,使CD=PC.
(1)如图1,延长BC到点E,使CE=BC,连接AE,DE.
①求证:BP∥DE;
②若BP⊥AC,求∠AED的度数;
(2)如图2,连接AD,若BP⊥AD,BP=1,则AD= .
【点拨】(1)①证明△DEC和△PBC全等得∠DEC=∠PBC,再根据平行线的判定可得出结论;
②延长AC交ED的延长线于F,根据等边三角形性质得BC=AC,∠ACB=60°,进而可求出∠CAE=∠CEA=30°,再由①BP∥DE,BP⊥AC得DE⊥AC,由此得∠CED=30°,据此可得∠AED的度数;
(2)延长BC到E是CE=BC,连接AE,DE,先求出∠BAE=90°,BE=4,由勾股定理得AE=,根据△DEC≌△PBC得BP=DE=1,再根据BP⊥AD,BP∥DE得DE⊥AD,然后由勾股定理即可求出AD的长.
【解析】(1)①证明:在△DEC和△PBC中,
,
∴△DEC≌△PBC(SAS),
∴∠DEC=∠PBC,
∴BP∥DE;
②解:延长AC交ED的延长线于F,如图1所示:
∵△ABC为等边三角形,
∴BC=AC,∠ACB=60°,
又∵CE=BC,
∴AC=CE,
∴∠CAE=∠CEA,
∵∠CAE+∠CEA=∠ACB=60°,
∴∠CAE=∠CEA=30°,
由①可知:BP∥DE,
∵BP⊥AC,
∴DE⊥AC,即∠F=90°,
又∵∠ECF=∠ACB=60°,
∴∠CED=90°﹣∠ECF=30°,
∴∠AED=∠CEA+∠CED=30°+30°=60°;
(2)延长BC到E是CE=BC,连接AE,DE,如图2所示:
由(1)②可知:∠CAE=30°,
∵△ABC为等边三角形,且边长为2,
∴AB=BC=AC=CE=2,∠BAC=60°,
∴∠BAE=∠BAC+∠CAE=90°,BE=BC+CE=4,
在Rt△ABE中,由勾股定理得:AE==,
由(1)①可知:△DEC≌△PBC,
∴BP=DE=1,
又∵BP⊥AD,BP∥DE,
∴DE⊥AD,
在Rt△ADE中,由勾股定理得:AD==.
故答案为:.
【点睛】此题主要考查了等边三角形的性质,全等三角形的判定和性质,勾股定理,理解等边三角形的性质,熟练掌握全等三角形的判定和性质,灵活运用勾股定理进行计算是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
