北师大九下3.7 切线长定理
图片预览




文档简介
(共25张PPT)
第三章 圆
3.7 切线长定理
北师大版 数学 九年级 下册
学习目标
1.理解切线长的概念,掌握切线长定理.
2.学会运用切线长定理解有关问题.
3.通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力,培养数形结合的思想.
情景导入
1、什么叫切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、什么是切线的性质定理?
圆的切线垂直于经过切点的半径.
情景导入
同学们打篮球吗?当你把篮球夹在腋下时,你能从中抽象出什么样数学图形?
核心知识点一:
切线长定理
B
A
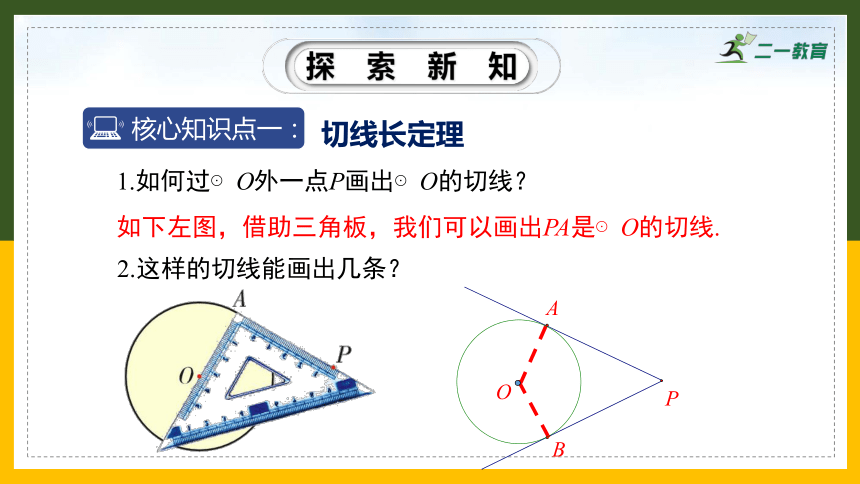
1.如何过⊙O外一点P画出⊙O的切线?
2.这样的切线能画出几条?
O
P
如下左图,借助三角板,我们可以画出PA是⊙O的切线.
探索新知
A
B
O
P
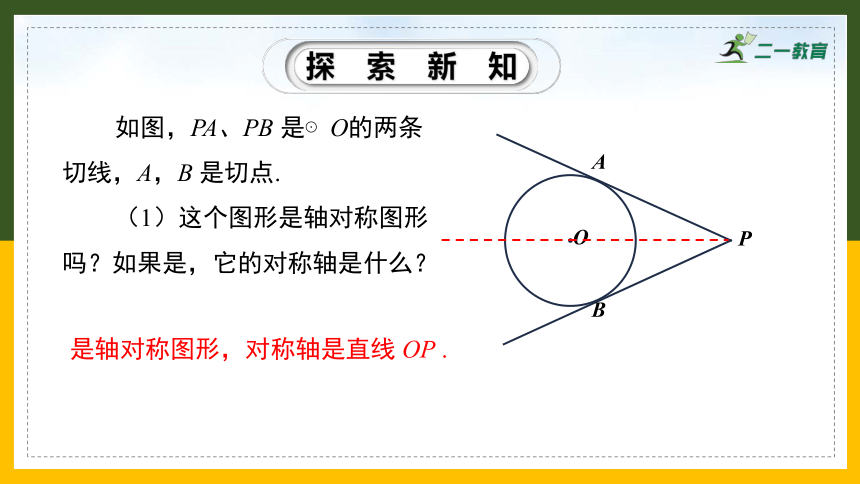
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
探索新知
A
B
O
P
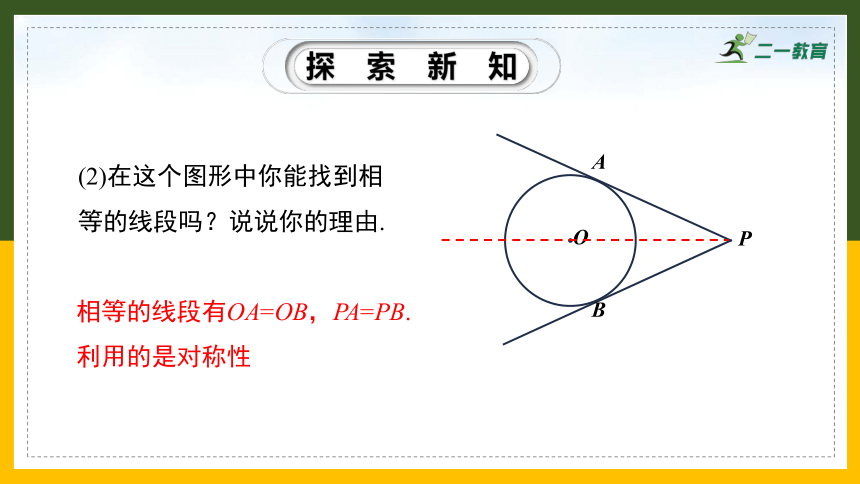
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
相等的线段有OA=OB,PA=PB.利用的是对称性
探索新知
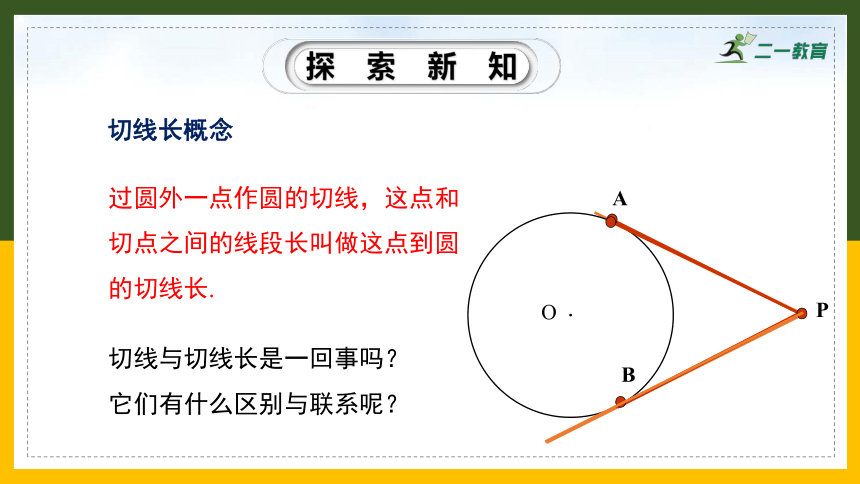
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
探索新知
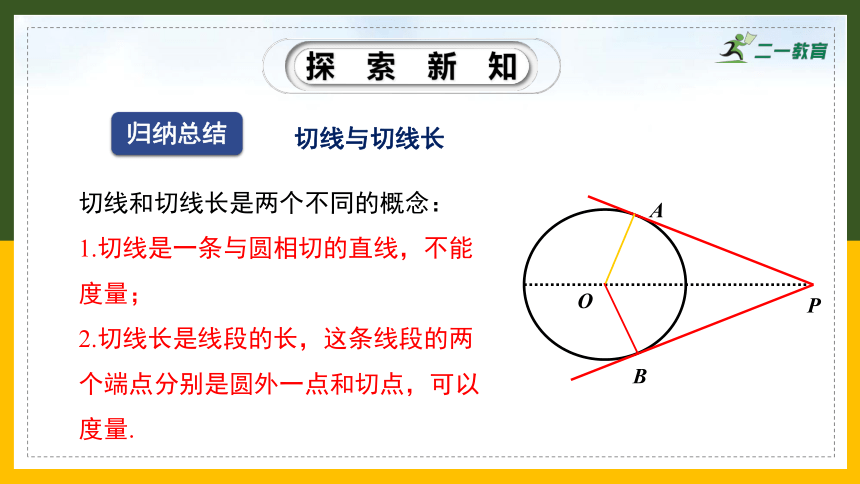
归纳总结
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
切线与切线长
探索新知
O
P
A
B
证明:连接OA,OB.
∵ PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°.
在Rt△AOP与Rt△BOP中,
∵ OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP.
∴ PA=PB.
已知:如图,PA,PB是⊙O的两条切线,A,B是切点.
求证: PA=PB.
探索新知
归纳总结
切线长定理
∵ PA,PB分别切⊙O于A,B,
∴ PA=PB , OP平分∠APB.
过圆外一点,所画的圆的两条切线的长相等.
几何语言:
O
P
A
B
探索新知
根据Rt△AOP与Rt△BOP全等,我们还可以得到其他一些什么结论?
O
P
A
B
还可以得到:
∠OPA=∠OPB,
∠POA=∠POB.
从而切线长定理可拓展为:过圆外一点画圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
探索新知
拓展:如图是轴对称图形吗?连接图中的两个切点 AB 交 OP 于点 C,又能得出什么结论?请把它们分类.
如图是轴对称图形,连接AB,结论:
①△PAB 是一个等腰三角形, 并且存在等腰三角形的“三线合一”定理.
②AB⊥OP,出现了圆的垂径定理.
探索新知
核心知识点二:
外切四边形
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
DN=DP,
AP=AL,
BL=BM,
CN=CM
L
M
N
P
探索新知
A
F
O
B
C
E
D
G
H
想一想:将上面四个等式左右两边分别相加,我们能得出什么结论?
圆外切四边形的性质:
圆外切四边形的两组对边和相等.
AE+BE+DG+CG=AH+BF+DH+CF
探索新知
当堂检测
1.如图所示,AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=10,AC=6,则BD的长是( )
A.3 B.4 C.5 D.6
B
当堂检测
2.如图所示,已知PA,PB分别切☉O于A,B,CD切☉O于E, PO=13, AO=5,则△PCD周长为( )
A.20 B.22 C.24 D.26
C
当堂检测
C
当堂检测
4.如图所示,四边形ABCD是☉O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
A
当堂检测
4
当堂检测
8.如图所示,AB为☉O的切线,AC,BD分别与☉O切于C,D点,若AB=5,AC=3,则BD的长是 .
2
当堂检测
9.如图所示,PA,PB分别与☉O相切于点A,B,AC为弦,BC为☉O的直径,∠P=60°,PB=2 cm.
(1)求证:△PAB是等边三角形;
(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∵∠P=60°,
∴△PAB是等边三角形.
当堂检测
(2)求AC的长.
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
感谢收看
第三章 圆
3.7 切线长定理
北师大版 数学 九年级 下册
学习目标
1.理解切线长的概念,掌握切线长定理.
2.学会运用切线长定理解有关问题.
3.通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力,培养数形结合的思想.
情景导入
1、什么叫切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
2、什么是切线的性质定理?
圆的切线垂直于经过切点的半径.
情景导入
同学们打篮球吗?当你把篮球夹在腋下时,你能从中抽象出什么样数学图形?
核心知识点一:
切线长定理
B
A
1.如何过⊙O外一点P画出⊙O的切线?
2.这样的切线能画出几条?
O
P
如下左图,借助三角板,我们可以画出PA是⊙O的切线.
探索新知
A
B
O
P
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
探索新知
A
B
O
P
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
相等的线段有OA=OB,PA=PB.利用的是对称性
探索新知
过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
·
O
P
A
B
切线与切线长是一回事吗?它们有什么区别与联系呢?
切线长概念
探索新知
归纳总结
切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
切线与切线长
探索新知
O
P
A
B
证明:连接OA,OB.
∵ PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°.
在Rt△AOP与Rt△BOP中,
∵ OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP.
∴ PA=PB.
已知:如图,PA,PB是⊙O的两条切线,A,B是切点.
求证: PA=PB.
探索新知
归纳总结
切线长定理
∵ PA,PB分别切⊙O于A,B,
∴ PA=PB , OP平分∠APB.
过圆外一点,所画的圆的两条切线的长相等.
几何语言:
O
P
A
B
探索新知
根据Rt△AOP与Rt△BOP全等,我们还可以得到其他一些什么结论?
O
P
A
B
还可以得到:
∠OPA=∠OPB,
∠POA=∠POB.
从而切线长定理可拓展为:过圆外一点画圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
探索新知
拓展:如图是轴对称图形吗?连接图中的两个切点 AB 交 OP 于点 C,又能得出什么结论?请把它们分类.
如图是轴对称图形,连接AB,结论:
①△PAB 是一个等腰三角形, 并且存在等腰三角形的“三线合一”定理.
②AB⊥OP,出现了圆的垂径定理.
探索新知
核心知识点二:
外切四边形
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
DN=DP,
AP=AL,
BL=BM,
CN=CM
L
M
N
P
探索新知
A
F
O
B
C
E
D
G
H
想一想:将上面四个等式左右两边分别相加,我们能得出什么结论?
圆外切四边形的性质:
圆外切四边形的两组对边和相等.
AE+BE+DG+CG=AH+BF+DH+CF
探索新知
当堂检测
1.如图所示,AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=10,AC=6,则BD的长是( )
A.3 B.4 C.5 D.6
B
当堂检测
2.如图所示,已知PA,PB分别切☉O于A,B,CD切☉O于E, PO=13, AO=5,则△PCD周长为( )
A.20 B.22 C.24 D.26
C
当堂检测
C
当堂检测
4.如图所示,四边形ABCD是☉O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为( )
A.44 B.42 C.46 D.47
A
当堂检测
4
当堂检测
8.如图所示,AB为☉O的切线,AC,BD分别与☉O切于C,D点,若AB=5,AC=3,则BD的长是 .
2
当堂检测
9.如图所示,PA,PB分别与☉O相切于点A,B,AC为弦,BC为☉O的直径,∠P=60°,PB=2 cm.
(1)求证:△PAB是等边三角形;
(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∵∠P=60°,
∴△PAB是等边三角形.
当堂检测
(2)求AC的长.
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
感谢收看
