北师大九下3.9 弧长及扇形的面积
图片预览





文档简介
(共26张PPT)
第三章 圆
3.9 弧长及扇形的面积
北师大版 数学 九年级 下册
学习目标
1.经历探索弧长计算公式和扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长计算公式和扇形面积计算公式,并运用公式解决问题;训练学生的数学运用能力.
情景导入
1.已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?
2.什么叫圆心角?
C=2πR,S=πR2.
角的顶点在圆心,角的两边分别与圆还有一个交点,这样的角叫做圆心角.
情景导入
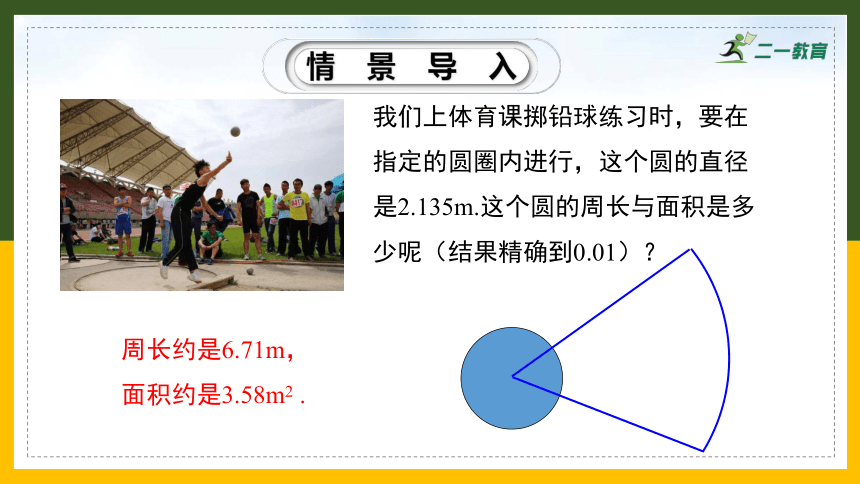
我们上体育课掷铅球练习时,要在指定的圆圈内进行,这个圆的直径是2.135m.这个圆的周长与面积是多少呢(结果精确到0.01)?
周长约是6.71m,
面积约是3.58m2 .
核心知识点一:
弧长的计算
(1)半径为R的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
(3)1°圆心角所对的弧长是多少?
C=2πR
360°
n°
o
探索新知
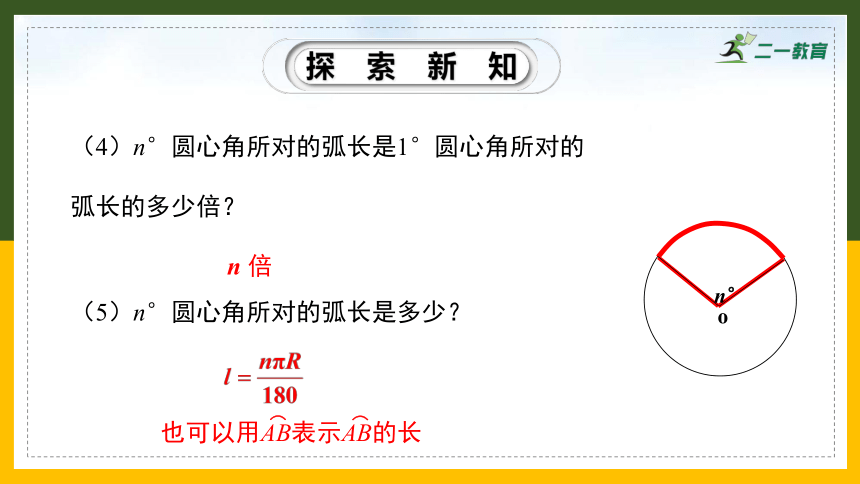
(4)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
(5)n°圆心角所对的弧长是多少?
n 倍
也可以用AB表示AB的长
⌒
⌒
n°
o
探索新知
O
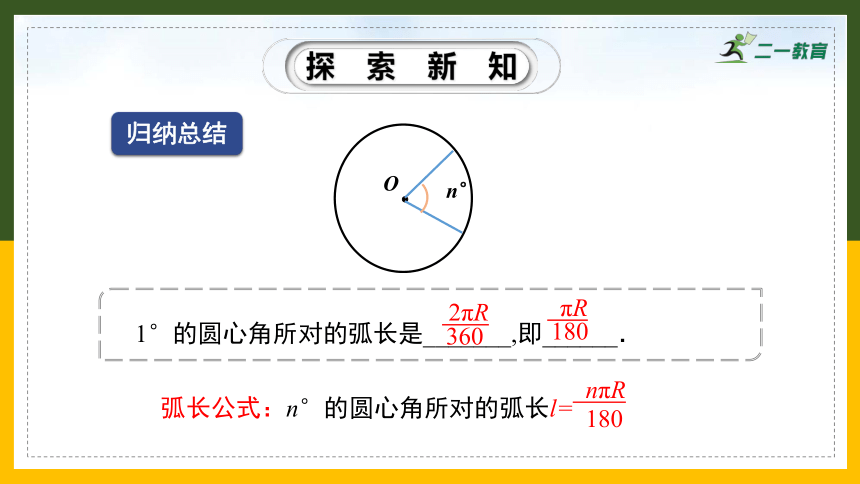
1°的圆心角所对的弧长是_______,即______.
2πR
360
πR
180
弧长公式:n°的圆心角所对的弧长l=
nπR
180
n°
归纳总结
探索新知
归纳总结
注意:(1)用弧长公式l= 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三个概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,只有在同圆或等圆中,才可能是等弧.
探索新知
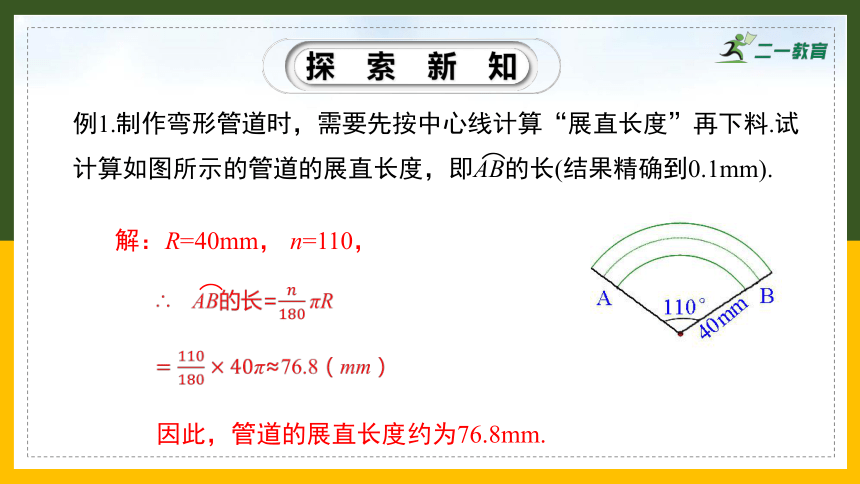
解:R=40mm, n=110,
︵
因此,管道的展直长度约为76.8mm.
例1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即AB的长(结果精确到0.1mm).
︵
探索新知
核心知识点二:
扇形面积的计算
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
扇形的定义:
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
图2
探索新知
圆心角是1°的扇形面积是多少?
圆心角为 n°的扇形面积是多少?
圆心角是1°的扇形面积是圆面积的
圆心角是n°的扇形面积是圆面积的
n°
1°
探索新知
扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
注意: n表示1°圆心角的倍数,它是不带单位的.
归纳总结
探索新知
扇形的弧长公式与面积公式的联系
A
B
O
O
探索新知
例2 . 在一块空旷的草地上有一根柱子,柱子上栓着一根长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
S=πR2=9π(m2)
探索新知
例3:如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)
O .
B
A
C
(1)截面上有水部分的面积是指图上哪一部分?
阴影部分.
探索新知
O.
B
A
C
D
(2)
O.
B
A
C
D
(3)
(2)水面高0.3 m是指哪一条线段的长?这条线段应该怎样画出来?
线段DC.过点O作OD垂直符号于AB并长交圆O于C.
(3)要求图中阴影部分面积,应该怎么办?
阴影部分面积=扇形OAB的面积-△OAB的面积
探索新知
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60 , ∠AOB=120 .
O.
B
A
C
D
(3)
探索新知
有水部分的面积:
S=S扇形OAB - S ΔOAB
O
B
A
C
D
(3)
探索新知
当堂检测
D
当堂检测
C
当堂检测
3.已知一个扇形的面积是24π,弧长是2π,则这个扇形的半径为( )
A.24 B.22 C.12 D.6
A
C
当堂检测
5. 一个扇形的弧长是10π cm,圆心角是150°,此扇形的面积为 (结果保留π).
60π cm2
当堂检测
当堂检测
弧长
计算公式:
扇形
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
感谢收看
第三章 圆
3.9 弧长及扇形的面积
北师大版 数学 九年级 下册
学习目标
1.经历探索弧长计算公式和扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长计算公式和扇形面积计算公式,并运用公式解决问题;训练学生的数学运用能力.
情景导入
1.已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?
2.什么叫圆心角?
C=2πR,S=πR2.
角的顶点在圆心,角的两边分别与圆还有一个交点,这样的角叫做圆心角.
情景导入
我们上体育课掷铅球练习时,要在指定的圆圈内进行,这个圆的直径是2.135m.这个圆的周长与面积是多少呢(结果精确到0.01)?
周长约是6.71m,
面积约是3.58m2 .
核心知识点一:
弧长的计算
(1)半径为R的圆,周长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
(3)1°圆心角所对的弧长是多少?
C=2πR
360°
n°
o
探索新知
(4)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
(5)n°圆心角所对的弧长是多少?
n 倍
也可以用AB表示AB的长
⌒
⌒
n°
o
探索新知
O
1°的圆心角所对的弧长是_______,即______.
2πR
360
πR
180
弧长公式:n°的圆心角所对的弧长l=
nπR
180
n°
归纳总结
探索新知
归纳总结
注意:(1)用弧长公式l= 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三个概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,只有在同圆或等圆中,才可能是等弧.
探索新知
解:R=40mm, n=110,
︵
因此,管道的展直长度约为76.8mm.
例1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即AB的长(结果精确到0.1mm).
︵
探索新知
核心知识点二:
扇形面积的计算
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
扇形的定义:
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
图2
探索新知
圆心角是1°的扇形面积是多少?
圆心角为 n°的扇形面积是多少?
圆心角是1°的扇形面积是圆面积的
圆心角是n°的扇形面积是圆面积的
n°
1°
探索新知
扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
注意: n表示1°圆心角的倍数,它是不带单位的.
归纳总结
探索新知
扇形的弧长公式与面积公式的联系
A
B
O
O
探索新知
例2 . 在一块空旷的草地上有一根柱子,柱子上栓着一根长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
S=πR2=9π(m2)
探索新知
例3:如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)
O .
B
A
C
(1)截面上有水部分的面积是指图上哪一部分?
阴影部分.
探索新知
O.
B
A
C
D
(2)
O.
B
A
C
D
(3)
(2)水面高0.3 m是指哪一条线段的长?这条线段应该怎样画出来?
线段DC.过点O作OD垂直符号于AB并长交圆O于C.
(3)要求图中阴影部分面积,应该怎么办?
阴影部分面积=扇形OAB的面积-△OAB的面积
探索新知
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60 , ∠AOB=120 .
O.
B
A
C
D
(3)
探索新知
有水部分的面积:
S=S扇形OAB - S ΔOAB
O
B
A
C
D
(3)
探索新知
当堂检测
D
当堂检测
C
当堂检测
3.已知一个扇形的面积是24π,弧长是2π,则这个扇形的半径为( )
A.24 B.22 C.12 D.6
A
C
当堂检测
5. 一个扇形的弧长是10π cm,圆心角是150°,此扇形的面积为 (结果保留π).
60π cm2
当堂检测
当堂检测
弧长
计算公式:
扇形
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
感谢收看
