北师大九下3.4.2 圆周角和圆心角的关系2
文档属性
| 名称 | 北师大九下3.4.2 圆周角和圆心角的关系2 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第三章 圆
3.4.2 圆周角和圆心角的关系2
北师大版 数学 九年级 下册
学习目标
1.掌握圆周角定理推论。
2.理解圆内接四边形定义及性质。
情景导入
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理推论:
圆周角定理:
同弧或等弧所对的圆周角相等.
情景导入
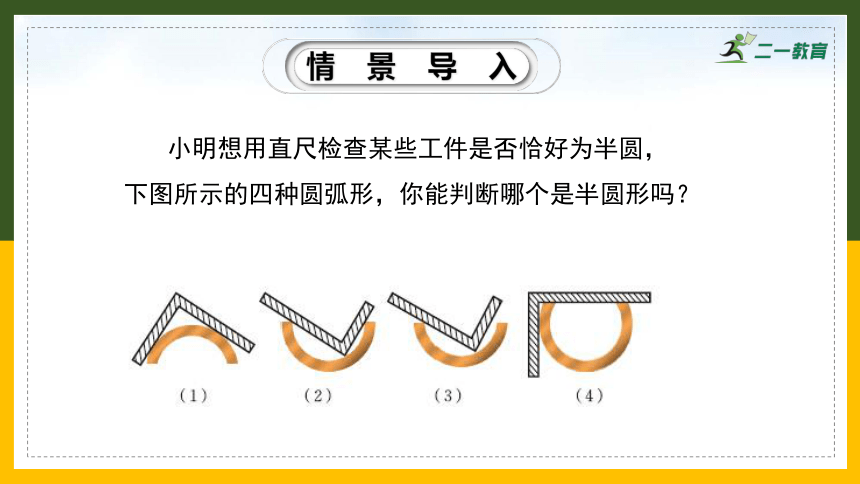
小明想用直尺检查某些工件是否恰好为半圆,下图所示的四种圆弧形,你能判断哪个是半圆形吗?
核心知识点一:
直径所对应的圆周角
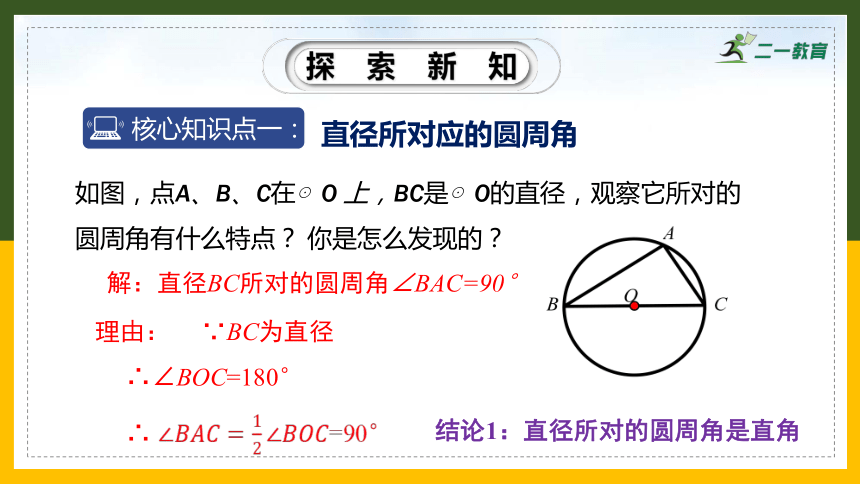
如图,点A、B、C在⊙O 上,BC是⊙O的直径,观察它所对的圆周角有什么特点? 你是怎么发现的?
解:直径BC所对的圆周角∠BAC=90°
结论1:直径所对的圆周角是直角
=90°
理由: ∵BC为直径
∴∠BOC=180°
∴
探索新知
观察图,圆周角∠BAC=90°,弦BC是直径吗?为什么?
解:弦BC是直径,连接OC、OB
∵∠BAC=90°
∴∠BOC=2∠BAC=180°
(圆周角的度数等于它所对弧上的圆心角的度数的一半)
∴B、O、C三点在同一直线上
∴BC是⊙O的一条直径
结论2:90°的圆周角所对的弦是直径
思考:这两个结论用什么定理证明?
圆周角定理
探索新知
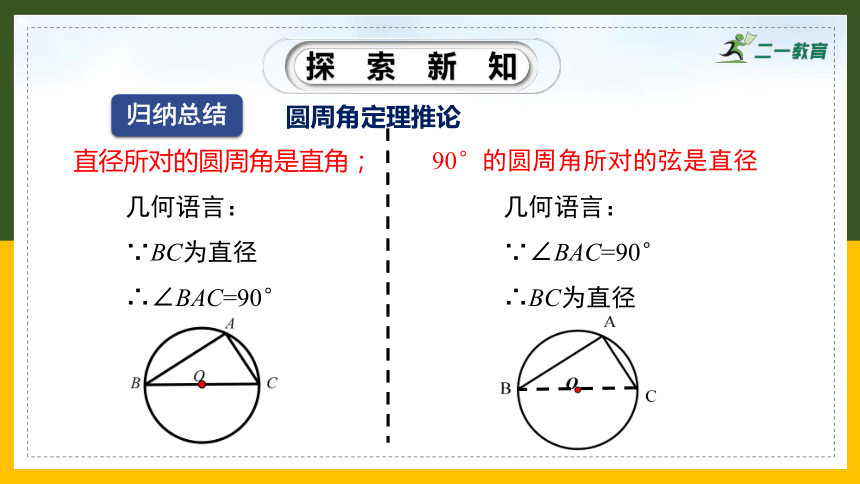
归纳总结
圆周角定理推论
直径所对的圆周角是直角;
几何语言:
∵BC为直径
∴∠BAC=90°
90°的圆周角所对的弦是直径
几何语言:
∵∠BAC=90°
∴BC为直径
探索新知
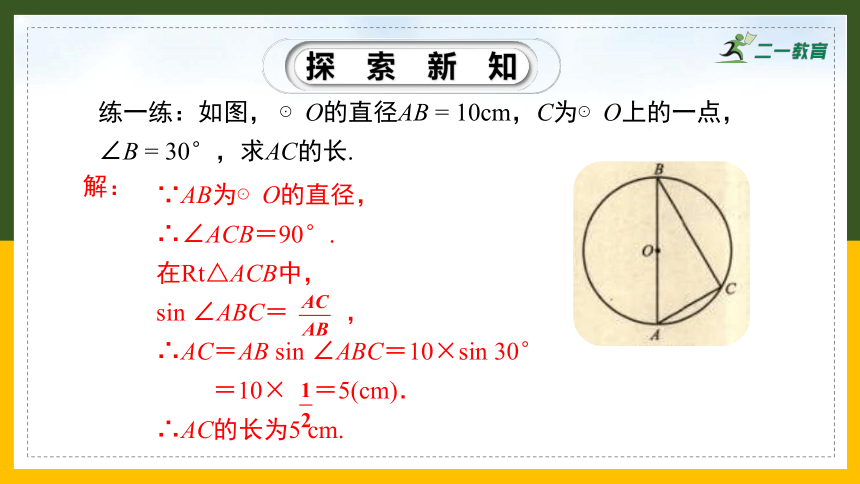
练一练:如图, ⊙O的直径AB = 10cm,C为⊙O上的一点,∠B = 30°,求AC的长.
∵AB为⊙O的直径,
∴∠ACB=90°.
在Rt△ACB中,
sin ∠ABC= ,
∴AC=AB sin ∠ABC=10×sin 30°
=10× =5(cm).
∴AC的长为5 cm.
解:
探索新知
解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.
归纳总结
探索新知
核心知识点二:
圆内接四边形及其性质
(1)如图,A,B,C,D是⊙O上的四点,AC为⊙O的直径,
请问∠BAD与∠BCD之间有什么关系?为什么?
解:∠BAD与∠BCD互补.
∵AC为直径,
∴∠ABC=90°,∠ADC=90°.
∵∠ABC+∠BCD+∠ADC+∠BAD=360°,
∴∠BAD+∠BCD=180°.
∴∠BAD与∠BCD互补.
A
B
C
O
D
探索新知
(2)若C点的位置发生了变化,∠BAD与∠BCD之间的关系
还成立吗?为什么?
A
B
C
O
D
1
2
∵ ∠2=2∠BAD,∠1=2∠BCD,
(圆周角的度数等于它所对弧上圆心角的一半),
∵∠1+∠2=360°,
∴∠BAD+∠BCD=180°.
∴∠BAD与∠BCD互补.
解:∠BAD与∠BCD的关系仍然成立.
如图8,连接OB,OD.
探索新知
(3)观察图9,两个四边形ABCD有什么共同的特点?
四边形ABCD的的四个顶点都在⊙O上,这样的四边形叫做圆内接四边形.这个圆叫做四边形的外接圆..
A
B
C
O
D
A
B
C
O
D
探索新知
A
B
C
O
D
(4)观察,∠BAD与∠BCD之间有什么关系?
圆内接四边形的对角互补.
几何语言:
∵四边形ABCD为圆内接四边形,
∴∠BAD+∠BCD=180°(圆内接四边形的对角互补).
A
B
C
O
D
探索新知
圆内接四边形外角的性质
思考:如图, ∠DCE是圆内接四边形ABCD的一个 外角,
∠A与∠DCE的大小有什么关系?
推论:圆内接四边形的一个外角等于它的内对角.
探索新知
证明:∠A=∠DCE.
∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°
(圆内角四边形的对角互补).
∵∠BCD+∠DCE=180°,
∴∠A=∠DCE.
A
B
C
O
D
E
探索新知
当堂检测
1.如图所示,AB为☉O的直径,点C在☉O上,∠A=30°,则∠B的度为( )
A.15° B.30° C.45° D.60°
D
当堂检测
2.如图所示,四边形ABCD内接于☉O,M为边CB延长线上一点.若∠AOC=98°,则∠ABM的度数是( )
A.42° B.49° C.51° D.59°
B
当堂检测
C
当堂检测
C
当堂检测
5.四边形ABCD内接于O,∠A∶∠B∶∠C∶∠D=5∶m∶4∶n,则m,n满足的条件是( )
A.5m=4n B. 4m=5n C.m+n=9 D.m+n=180°
6.如图所示,四边形ABCD内接于☉O,OC∥AD,∠DAB=60°,∠ADC=106°,
则∠OCB等于 °.
C
46
当堂检测
7.如图所示,在圆内接四边形ADBC中,DC=DB,M为CA延长线上一点.
求证:AD平分∠BAM.
证明:∵四边形ADBC是圆内接四边形,
∴∠MAD=∠DBC,∠DAB=∠DCB.
∵DC=DB,
∴∠DBC=∠DCB,
∴∠MAD=∠DAB,
即AD平分∠BAM.
当堂检测
8.如图所示,在☉O中,有内接四边形ABCD,AB=AD,E为弧AD上一点.
(1)若∠C=110°,求∠BAD和∠E的度数;
(1)解:∵四边形ABCD内接于☉O,
∴∠BAD+∠C=180°.
∵∠C=110°,∴∠BAD=70°.
∵AB=AD,∴∠ABD=∠ADB=55°.
∵四边形ABDE内接于☉O,
∴∠ABD+∠E=180°,∴∠E=125°.
当堂检测
(2)若∠E=∠C,求证:△ABD为等边三角形.
(2)证明:∵四边形ABCD是☉O的内接四边形,
∴∠BAD+∠C=180°.
∵四边形ABDE是☉O的内接四边形,
∴∠ABD+∠E=180°.
又∵∠E=∠C,∴∠BAD=∠ABD,
∴AD=BD.
∵AB=AD,∴AD=BD=AB,
∴△ABD为等边三角形.
圆周角定理
推论2
推论3
圆内接四边形的对角互补.
直径所所对的圆周角是直角;
90°的圆周角所对的弦是直径
感谢收看
第三章 圆
3.4.2 圆周角和圆心角的关系2
北师大版 数学 九年级 下册
学习目标
1.掌握圆周角定理推论。
2.理解圆内接四边形定义及性质。
情景导入
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理推论:
圆周角定理:
同弧或等弧所对的圆周角相等.
情景导入
小明想用直尺检查某些工件是否恰好为半圆,下图所示的四种圆弧形,你能判断哪个是半圆形吗?
核心知识点一:
直径所对应的圆周角
如图,点A、B、C在⊙O 上,BC是⊙O的直径,观察它所对的圆周角有什么特点? 你是怎么发现的?
解:直径BC所对的圆周角∠BAC=90°
结论1:直径所对的圆周角是直角
=90°
理由: ∵BC为直径
∴∠BOC=180°
∴
探索新知
观察图,圆周角∠BAC=90°,弦BC是直径吗?为什么?
解:弦BC是直径,连接OC、OB
∵∠BAC=90°
∴∠BOC=2∠BAC=180°
(圆周角的度数等于它所对弧上的圆心角的度数的一半)
∴B、O、C三点在同一直线上
∴BC是⊙O的一条直径
结论2:90°的圆周角所对的弦是直径
思考:这两个结论用什么定理证明?
圆周角定理
探索新知
归纳总结
圆周角定理推论
直径所对的圆周角是直角;
几何语言:
∵BC为直径
∴∠BAC=90°
90°的圆周角所对的弦是直径
几何语言:
∵∠BAC=90°
∴BC为直径
探索新知
练一练:如图, ⊙O的直径AB = 10cm,C为⊙O上的一点,∠B = 30°,求AC的长.
∵AB为⊙O的直径,
∴∠ACB=90°.
在Rt△ACB中,
sin ∠ABC= ,
∴AC=AB sin ∠ABC=10×sin 30°
=10× =5(cm).
∴AC的长为5 cm.
解:
探索新知
解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.
归纳总结
探索新知
核心知识点二:
圆内接四边形及其性质
(1)如图,A,B,C,D是⊙O上的四点,AC为⊙O的直径,
请问∠BAD与∠BCD之间有什么关系?为什么?
解:∠BAD与∠BCD互补.
∵AC为直径,
∴∠ABC=90°,∠ADC=90°.
∵∠ABC+∠BCD+∠ADC+∠BAD=360°,
∴∠BAD+∠BCD=180°.
∴∠BAD与∠BCD互补.
A
B
C
O
D
探索新知
(2)若C点的位置发生了变化,∠BAD与∠BCD之间的关系
还成立吗?为什么?
A
B
C
O
D
1
2
∵ ∠2=2∠BAD,∠1=2∠BCD,
(圆周角的度数等于它所对弧上圆心角的一半),
∵∠1+∠2=360°,
∴∠BAD+∠BCD=180°.
∴∠BAD与∠BCD互补.
解:∠BAD与∠BCD的关系仍然成立.
如图8,连接OB,OD.
探索新知
(3)观察图9,两个四边形ABCD有什么共同的特点?
四边形ABCD的的四个顶点都在⊙O上,这样的四边形叫做圆内接四边形.这个圆叫做四边形的外接圆..
A
B
C
O
D
A
B
C
O
D
探索新知
A
B
C
O
D
(4)观察,∠BAD与∠BCD之间有什么关系?
圆内接四边形的对角互补.
几何语言:
∵四边形ABCD为圆内接四边形,
∴∠BAD+∠BCD=180°(圆内接四边形的对角互补).
A
B
C
O
D
探索新知
圆内接四边形外角的性质
思考:如图, ∠DCE是圆内接四边形ABCD的一个 外角,
∠A与∠DCE的大小有什么关系?
推论:圆内接四边形的一个外角等于它的内对角.
探索新知
证明:∠A=∠DCE.
∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°
(圆内角四边形的对角互补).
∵∠BCD+∠DCE=180°,
∴∠A=∠DCE.
A
B
C
O
D
E
探索新知
当堂检测
1.如图所示,AB为☉O的直径,点C在☉O上,∠A=30°,则∠B的度为( )
A.15° B.30° C.45° D.60°
D
当堂检测
2.如图所示,四边形ABCD内接于☉O,M为边CB延长线上一点.若∠AOC=98°,则∠ABM的度数是( )
A.42° B.49° C.51° D.59°
B
当堂检测
C
当堂检测
C
当堂检测
5.四边形ABCD内接于O,∠A∶∠B∶∠C∶∠D=5∶m∶4∶n,则m,n满足的条件是( )
A.5m=4n B. 4m=5n C.m+n=9 D.m+n=180°
6.如图所示,四边形ABCD内接于☉O,OC∥AD,∠DAB=60°,∠ADC=106°,
则∠OCB等于 °.
C
46
当堂检测
7.如图所示,在圆内接四边形ADBC中,DC=DB,M为CA延长线上一点.
求证:AD平分∠BAM.
证明:∵四边形ADBC是圆内接四边形,
∴∠MAD=∠DBC,∠DAB=∠DCB.
∵DC=DB,
∴∠DBC=∠DCB,
∴∠MAD=∠DAB,
即AD平分∠BAM.
当堂检测
8.如图所示,在☉O中,有内接四边形ABCD,AB=AD,E为弧AD上一点.
(1)若∠C=110°,求∠BAD和∠E的度数;
(1)解:∵四边形ABCD内接于☉O,
∴∠BAD+∠C=180°.
∵∠C=110°,∴∠BAD=70°.
∵AB=AD,∴∠ABD=∠ADB=55°.
∵四边形ABDE内接于☉O,
∴∠ABD+∠E=180°,∴∠E=125°.
当堂检测
(2)若∠E=∠C,求证:△ABD为等边三角形.
(2)证明:∵四边形ABCD是☉O的内接四边形,
∴∠BAD+∠C=180°.
∵四边形ABDE是☉O的内接四边形,
∴∠ABD+∠E=180°.
又∵∠E=∠C,∴∠BAD=∠ABD,
∴AD=BD.
∵AB=AD,∴AD=BD=AB,
∴△ABD为等边三角形.
圆周角定理
推论2
推论3
圆内接四边形的对角互补.
直径所所对的圆周角是直角;
90°的圆周角所对的弦是直径
感谢收看
