北师大九下3.5 确定圆的条件
图片预览





文档简介
(共26张PPT)
第三章 圆
3.5 确定圆的条件
北师大版 数学 九年级 下册
学习目标
一、理解不在同一直线上的三个点确定一个圆并掌握它的运用.
二、了解三角形的外接圆和三角形外心的概念.
情景导入
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
思考: 要确定一个圆必须满足几个条件
核心知识点一:
探索确定圆的条件
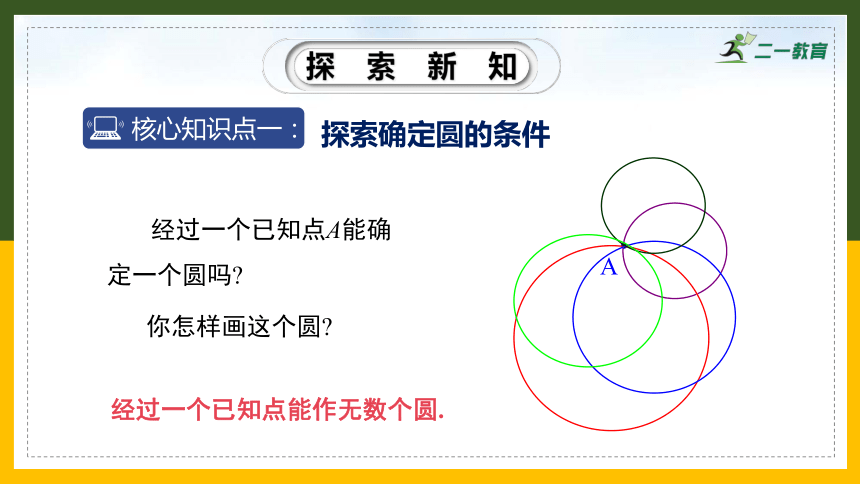
经过一个已知点A能确定一个圆吗
你怎样画这个圆
A
经过一个已知点能作无数个圆.
探索新知
A
经过两个已知点A、B能确
定一个圆吗
经过两个已知点A、B能作无数个圆
经过两个已知点A、B
所作的圆的圆心在怎
样的一条直线上
它们的圆心都在线段AB的中垂线上.
探索新知
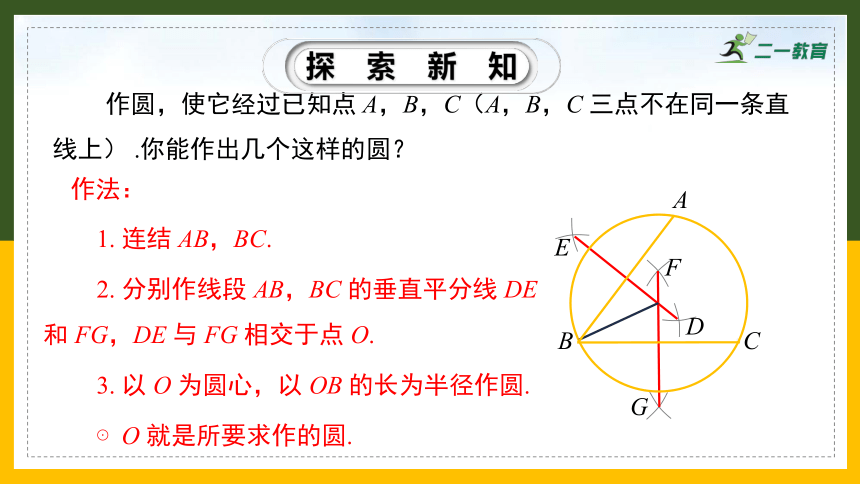
作圆,使它经过已知点 A,B,C(A,B,C 三点不在同一条直线上) .你能作出几个这样的圆?
B
A
C
E
F
1. 连结 AB,BC.
2. 分别作线段 AB,BC 的垂直平分线 DE 和 FG,DE 与 FG 相交于点 O.
3. 以 O 为圆心,以 OB 的长为半径作圆.
⊙O 就是所要求作的圆.
作法:
G
D
探索新知
说说以上作法的道理.
在上面的作图过程中,因为直线 DE 和 FG 只有一个交点 O,并且点 O 到 A,B,C 三个点的距离相等,所以经过 A,B,C 三个点可以作一个圆,并且只能作一个圆..
B
A
C
E
G
D
F
O
探索新知
归纳总结
定理:
不在同一直线上的三点确定一个圆.
位置关系
有且只有
探索新知
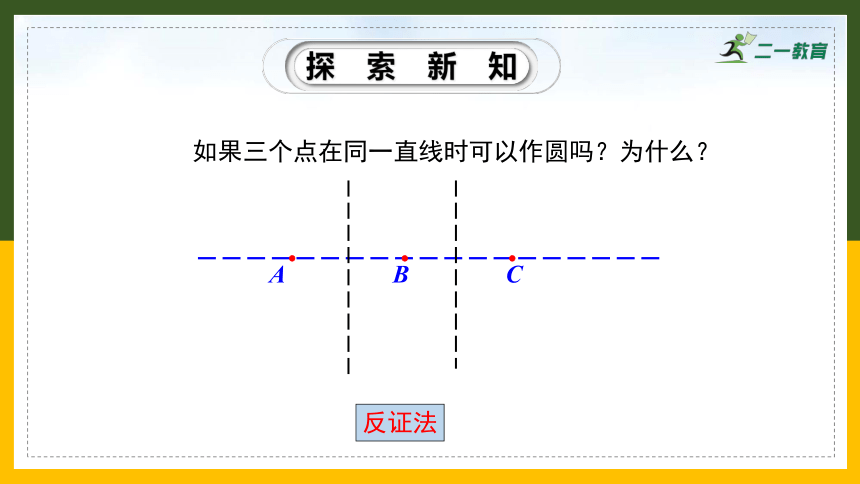
如果三个点在同一直线时可以作圆吗?为什么?
A
B
C
反证法
探索新知
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到A、B、C三点的距离都相等,
即圆心是线段AB、BC垂直平分线的交点.
分别作AB、BC垂直平分线l1、l2.
显然l1∥l2,
l1与l2无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
A
B
C
l1
l2
探索新知
现在你知道了怎样要将一个如图的破损的圆盘复原了吗?
方法:
1. 在圆弧上任取三点 A,B,C;
2. 作线段 AB,BC 的
垂直平分线,其交点
O 即为圆心;
3. 以点 O 为圆心,OC 长为半径作圆.⊙O 即为所求.
A
B
C
O
探索新知
核心知识点二:
三角形的外接圆及外心
A
B
C
O
已知△ABC,用直尺和圆规作出过点A、B、C的圆.
探索新知
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
归纳总结
探索新知
C
A
B
O
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
探索新知
三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一
点的距离为半径作圆即可.
归纳总结
探索新知
分别作出锐角三角形、直角三角形、钝角三角形的外接圆,并说明它们外心的位置情况.
锐角三角形的外心位于三角形内
A
B
C
● O
A
B
C
C
A
B
┐
● O
●O
直角三角形的外心位于直角三角形斜边中点处
钝角三角形的外心位于三角形外
探索新知
归纳总结
求三角形的外接圆半径的方法:
求三角形的外接圆半径时, 最常用的方法是作出圆心与三角形顶点的连线( 即半径),或延长使这条半径变为直径, 将求半径转化为直角三角形中求边的长.
探索新知
当堂检测
1.下列命题不正确的是 ( )
A.三点确定一个圆
B.三角形的外接圆有且只有一个
C.经过一点有无数个圆
D.经过两点有无数个圆
A
当堂检测
2.小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是 ( )
A.AB,AC边上的中线的交点
B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的平分线的交点
B
当堂检测
3.如图,☉O是等边三角形ABC的外接圆,D是弧AC上一动点(不与点A,C重合),下列结论:①∠ADB=∠BDC;②DA=DC;③当DB最长时,DB=2DC;④DA+DC=DB,其中一定正确的结论有 ( )
A.1个 B.2个
C.3个 D.4个
C
当堂检测
4.下列命题中是假命题的是 ( )
A.三角形的外心到三角形三个顶点的距离相等
B.三角形的外心到三角形三边的距离相等
C.三角形的外心一定在三角形的中垂线上
D.三角形任意两边中垂线的交点是这个三角形的外心
B
当堂检测
5.如图,在正方形网格中,每个小正方形的边长都是1,☉O是△ABC的外接圆,点A,B,O在网格线的交点上,则sin∠ACB的值是 .
当堂检测
6.如图所示,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
当堂检测
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
感谢收看
第三章 圆
3.5 确定圆的条件
北师大版 数学 九年级 下册
学习目标
一、理解不在同一直线上的三个点确定一个圆并掌握它的运用.
二、了解三角形的外接圆和三角形外心的概念.
情景导入
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
思考: 要确定一个圆必须满足几个条件
核心知识点一:
探索确定圆的条件
经过一个已知点A能确定一个圆吗
你怎样画这个圆
A
经过一个已知点能作无数个圆.
探索新知
A
经过两个已知点A、B能确
定一个圆吗
经过两个已知点A、B能作无数个圆
经过两个已知点A、B
所作的圆的圆心在怎
样的一条直线上
它们的圆心都在线段AB的中垂线上.
探索新知
作圆,使它经过已知点 A,B,C(A,B,C 三点不在同一条直线上) .你能作出几个这样的圆?
B
A
C
E
F
1. 连结 AB,BC.
2. 分别作线段 AB,BC 的垂直平分线 DE 和 FG,DE 与 FG 相交于点 O.
3. 以 O 为圆心,以 OB 的长为半径作圆.
⊙O 就是所要求作的圆.
作法:
G
D
探索新知
说说以上作法的道理.
在上面的作图过程中,因为直线 DE 和 FG 只有一个交点 O,并且点 O 到 A,B,C 三个点的距离相等,所以经过 A,B,C 三个点可以作一个圆,并且只能作一个圆..
B
A
C
E
G
D
F
O
探索新知
归纳总结
定理:
不在同一直线上的三点确定一个圆.
位置关系
有且只有
探索新知
如果三个点在同一直线时可以作圆吗?为什么?
A
B
C
反证法
探索新知
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到A、B、C三点的距离都相等,
即圆心是线段AB、BC垂直平分线的交点.
分别作AB、BC垂直平分线l1、l2.
显然l1∥l2,
l1与l2无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
A
B
C
l1
l2
探索新知
现在你知道了怎样要将一个如图的破损的圆盘复原了吗?
方法:
1. 在圆弧上任取三点 A,B,C;
2. 作线段 AB,BC 的
垂直平分线,其交点
O 即为圆心;
3. 以点 O 为圆心,OC 长为半径作圆.⊙O 即为所求.
A
B
C
O
探索新知
核心知识点二:
三角形的外接圆及外心
A
B
C
O
已知△ABC,用直尺和圆规作出过点A、B、C的圆.
探索新知
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
归纳总结
探索新知
C
A
B
O
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
探索新知
三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一
点的距离为半径作圆即可.
归纳总结
探索新知
分别作出锐角三角形、直角三角形、钝角三角形的外接圆,并说明它们外心的位置情况.
锐角三角形的外心位于三角形内
A
B
C
● O
A
B
C
C
A
B
┐
● O
●O
直角三角形的外心位于直角三角形斜边中点处
钝角三角形的外心位于三角形外
探索新知
归纳总结
求三角形的外接圆半径的方法:
求三角形的外接圆半径时, 最常用的方法是作出圆心与三角形顶点的连线( 即半径),或延长使这条半径变为直径, 将求半径转化为直角三角形中求边的长.
探索新知
当堂检测
1.下列命题不正确的是 ( )
A.三点确定一个圆
B.三角形的外接圆有且只有一个
C.经过一点有无数个圆
D.经过两点有无数个圆
A
当堂检测
2.小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是 ( )
A.AB,AC边上的中线的交点
B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的平分线的交点
B
当堂检测
3.如图,☉O是等边三角形ABC的外接圆,D是弧AC上一动点(不与点A,C重合),下列结论:①∠ADB=∠BDC;②DA=DC;③当DB最长时,DB=2DC;④DA+DC=DB,其中一定正确的结论有 ( )
A.1个 B.2个
C.3个 D.4个
C
当堂检测
4.下列命题中是假命题的是 ( )
A.三角形的外心到三角形三个顶点的距离相等
B.三角形的外心到三角形三边的距离相等
C.三角形的外心一定在三角形的中垂线上
D.三角形任意两边中垂线的交点是这个三角形的外心
B
当堂检测
5.如图,在正方形网格中,每个小正方形的边长都是1,☉O是△ABC的外接圆,点A,B,O在网格线的交点上,则sin∠ACB的值是 .
当堂检测
6.如图所示,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
当堂检测
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
感谢收看
