北师大九下3.6.1 直线和圆的位置关系1
文档属性
| 名称 | 北师大九下3.6.1 直线和圆的位置关系1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
第三章 圆
3.6.1 直线和圆的位置关系1
北师大版 数学 九年级 下册
学习目标
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离与半径之间的关系来判定它们.
2.掌握直线与圆相切的判断方法和如何作出直线与圆相切,并能利用公共点的个数和圆心到直线的距离与半径之间的关系来判定.
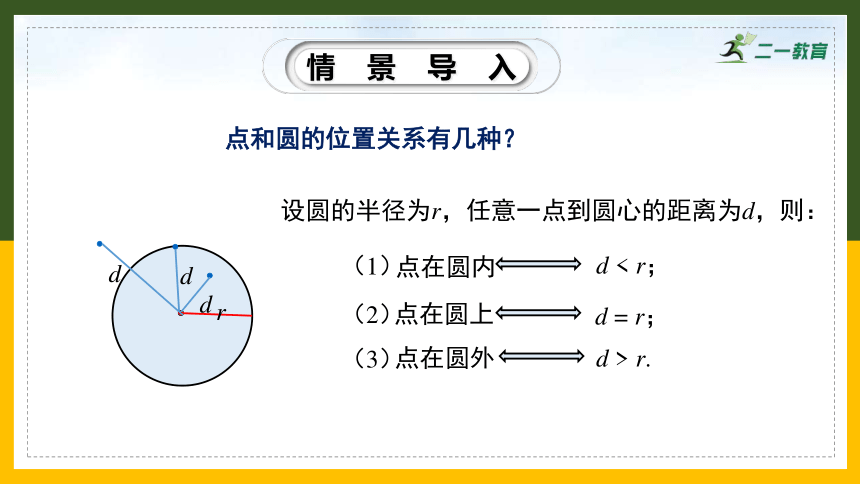
情景导入
点和圆的位置关系有几种?
(3)
r
(1)
d < r;
d > r.
点在圆外
点在圆内
(2)
d = r;
点在圆上
设圆的半径为r,任意一点到圆心的距离为d,则:
d
d
d
情景导入
直线和圆的位置关系有几种?
核心知识点一:
用定义判断直线与圆的位置关系
仔细观察太阳与地平线的位置关系.
观察:如果把太阳看作一个圆,地平线看作是一条直线,由此,你发现它们有几种位置关系?分别有几个交点?
探索新知
想一想:
(1)直线与圆有哪几种位置关系?
直线与圆的位置关系①:相离
特征:公共点个数0个
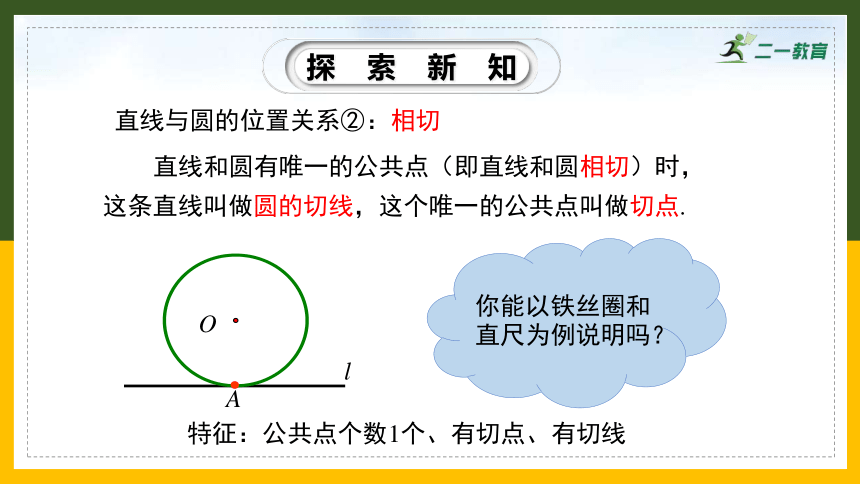
探索新知
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
你能以铁丝圈和直尺为例说明吗?
l
O
A
直线与圆的位置关系②:相切
特征:公共点个数1个、有切点、有切线
探索新知
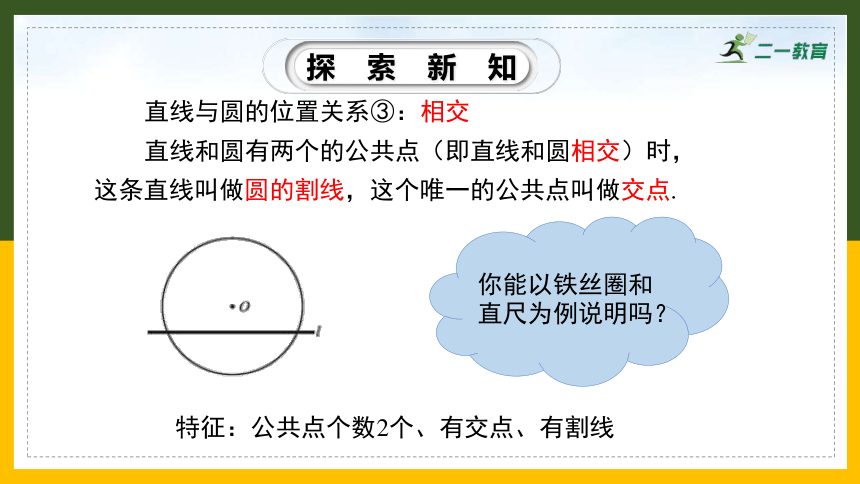
直线与圆的位置关系③:相交
直线和圆有两个的公共点(即直线和圆相交)时,这条直线叫做圆的割线,这个唯一的公共点叫做交点.
你能以铁丝圈和直尺为例说明吗?
特征:公共点个数2个、有交点、有割线
探索新知
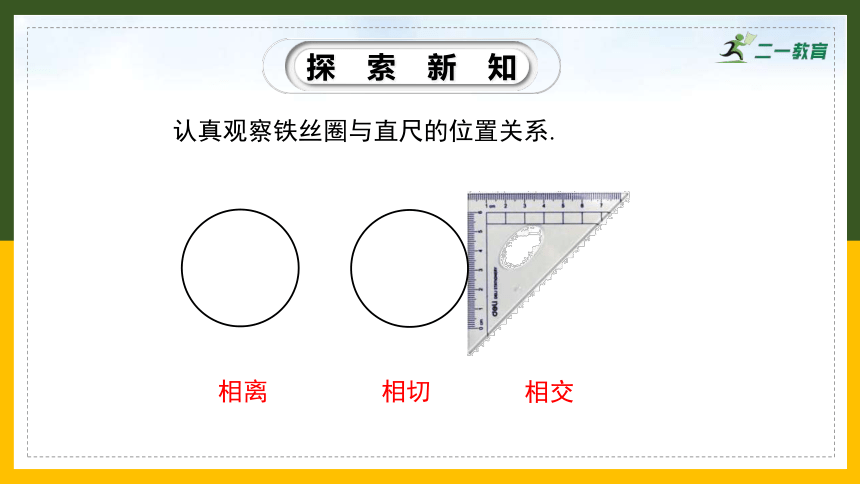
认真观察铁丝圈与直尺的位置关系.
相离
相切
相交
探索新知
核心知识点二:
用数量关系判断直线与圆的位置关系
如图,圆心 O 到直线 l 的距离 d 与⊙O 的半径 r 的大小有什么关系?你能根据 d 与 r 的大小关系确定直线与圆的位置关系吗?
O
l
O
l
O
l
相交
相切
相离
d
r
d
r
d
r
d < r
d = r
d > r
探索新知
归纳总结
直线和圆的位置关系:
(1) 直线和圆相交
(2) 直线和圆相切
(3) 直线和圆相离
d < r
d = r
d > r
图形关系
数量关系
探索新知
直线和圆的位置关系 相 交 相 切 相 离
图 形
公共点个数
公共点名称 -
直线名称 -
距离 d 与半径 r 的关系
l
O
d
r
l
O
A
B
d
r
l
O
A
d
r
2 个
交点
割线
1 个
切点
切线
d<r
d=r
d>r
没有
探索新知
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由直线与圆的公共点的个数来判断;
(2)根据性质,由圆心到直线的距离 d 与半径 r 的关系来判断.
两
归纳总结
探索新知
核心知识点三:
圆的切线的性质
前面我们已学过的切线的性质有哪些?
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
切线还有什么性质?
探索新知
如图,直线 CD与 ⊙O 相切于点 A,直径 AB 与直线 CD 有怎样的位置关系?说说你的理由.
直径 AB 垂直于直线 CD.
小颖的理由是:
∵圆是轴对称图形,AB 是对称轴,
∴沿直线 AB 对折图形时,AC 与 AD 重合,
因此∠BAC=∠BAD= 90°.
C
D
B
●O
A
探索新知
小亮的理由是:
直径 AB 与直线 CD 垂直.
假设 AB 与 CD 不垂直,过点 O 作一条直径垂直于 CD,垂足为点 M,如图,
则OM < OA,即圆心到直线 CD 的距离小于 ⊙O 的半径,
因此 CD 与 ⊙O 相交.
这与已知条件“直线与 ⊙O 相切”相矛盾.
所以 AB 与 CD 垂直.
C
D
B
●O
A
M
探索新知
圆的切线垂直于过切点的半径.
几何语言:
∵CD 是 ⊙O 的切线,A 是切点,OA 是 ⊙O 的半径,
∴CD⊥OA.
提示:切线的性质定理是证明两线垂直的重要根据;
作过切点的半径是常用经验辅助线之一.
C
D
B
●O
A
归纳总结
切线的性质定理:
探索新知
当堂检测
1.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
A
当堂检测
2.经过☉O的直径的一端能作 条☉O的切线( )
A.0 B.1 C.2 D.3
B
C
当堂检测
4.如图所示,PA,PB是☉O的切线,A,B是切点,点C为☉O上一点,若∠P=40°,则∠ACB的度数为( )
A.70° B.50°
C.20° D.40°
A
当堂检测
5.已知☉O的半径是一元二次方程x2-5x-6=0的一个根,圆心O到直线l的距离d=4,则直线l与☉O的位置关系是( )
A.相交 B.相切
C.相离 D.平行
6.如图所示,过☉O外一点P作圆的切线PA,PB,
点A,B为切点,AC为直径,设∠P=m°,∠C=n°,
则m,n之间的数量关系为 .
A
m+2n=180
当堂检测
3
当堂检测
8.如图所示,BC是☉O的直径,CE是☉O的弦,过点E作☉O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.
(1)求证:∠ABG=2∠C;
(1)证明:如图所示,连接OE.
∵EG是☉O的切线,
∴OE⊥EG.
∵BF⊥GE,∴OE∥AB,∴∠A=∠OEC.
∵OE=OC,∴∠OEC=∠C,∴∠A=∠C.
∵∠ABG=∠A+∠C,∴∠ABG=2∠C.
当堂检测
直线和圆的位置关系及切线的性质
直线和圆的位置关系的性质
直线和圆的三种位置关系
相交:直线和圆有两个公共点
相切:直线和圆有一个公共点
相离:直线和圆没有公共点
(1) 直线和圆相交;d(2) 直线和圆相切;d=r
(3) 直线和圆相离;d>r
切线的性质
圆的切线垂直于经过切点的半径.
感谢收看
第三章 圆
3.6.1 直线和圆的位置关系1
北师大版 数学 九年级 下册
学习目标
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离与半径之间的关系来判定它们.
2.掌握直线与圆相切的判断方法和如何作出直线与圆相切,并能利用公共点的个数和圆心到直线的距离与半径之间的关系来判定.
情景导入
点和圆的位置关系有几种?
(3)
r
(1)
d < r;
d > r.
点在圆外
点在圆内
(2)
d = r;
点在圆上
设圆的半径为r,任意一点到圆心的距离为d,则:
d
d
d
情景导入
直线和圆的位置关系有几种?
核心知识点一:
用定义判断直线与圆的位置关系
仔细观察太阳与地平线的位置关系.
观察:如果把太阳看作一个圆,地平线看作是一条直线,由此,你发现它们有几种位置关系?分别有几个交点?
探索新知
想一想:
(1)直线与圆有哪几种位置关系?
直线与圆的位置关系①:相离
特征:公共点个数0个
探索新知
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
你能以铁丝圈和直尺为例说明吗?
l
O
A
直线与圆的位置关系②:相切
特征:公共点个数1个、有切点、有切线
探索新知
直线与圆的位置关系③:相交
直线和圆有两个的公共点(即直线和圆相交)时,这条直线叫做圆的割线,这个唯一的公共点叫做交点.
你能以铁丝圈和直尺为例说明吗?
特征:公共点个数2个、有交点、有割线
探索新知
认真观察铁丝圈与直尺的位置关系.
相离
相切
相交
探索新知
核心知识点二:
用数量关系判断直线与圆的位置关系
如图,圆心 O 到直线 l 的距离 d 与⊙O 的半径 r 的大小有什么关系?你能根据 d 与 r 的大小关系确定直线与圆的位置关系吗?
O
l
O
l
O
l
相交
相切
相离
d
r
d
r
d
r
d < r
d = r
d > r
探索新知
归纳总结
直线和圆的位置关系:
(1) 直线和圆相交
(2) 直线和圆相切
(3) 直线和圆相离
d < r
d = r
d > r
图形关系
数量关系
探索新知
直线和圆的位置关系 相 交 相 切 相 离
图 形
公共点个数
公共点名称 -
直线名称 -
距离 d 与半径 r 的关系
l
O
d
r
l
O
A
B
d
r
l
O
A
d
r
2 个
交点
割线
1 个
切点
切线
d<r
d=r
d>r
没有
探索新知
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由直线与圆的公共点的个数来判断;
(2)根据性质,由圆心到直线的距离 d 与半径 r 的关系来判断.
两
归纳总结
探索新知
核心知识点三:
圆的切线的性质
前面我们已学过的切线的性质有哪些?
①切线和圆有且只有一个公共点;
②切线和圆心的距离等于半径.
切线还有什么性质?
探索新知
如图,直线 CD与 ⊙O 相切于点 A,直径 AB 与直线 CD 有怎样的位置关系?说说你的理由.
直径 AB 垂直于直线 CD.
小颖的理由是:
∵圆是轴对称图形,AB 是对称轴,
∴沿直线 AB 对折图形时,AC 与 AD 重合,
因此∠BAC=∠BAD= 90°.
C
D
B
●O
A
探索新知
小亮的理由是:
直径 AB 与直线 CD 垂直.
假设 AB 与 CD 不垂直,过点 O 作一条直径垂直于 CD,垂足为点 M,如图,
则OM < OA,即圆心到直线 CD 的距离小于 ⊙O 的半径,
因此 CD 与 ⊙O 相交.
这与已知条件“直线与 ⊙O 相切”相矛盾.
所以 AB 与 CD 垂直.
C
D
B
●O
A
M
探索新知
圆的切线垂直于过切点的半径.
几何语言:
∵CD 是 ⊙O 的切线,A 是切点,OA 是 ⊙O 的半径,
∴CD⊥OA.
提示:切线的性质定理是证明两线垂直的重要根据;
作过切点的半径是常用经验辅助线之一.
C
D
B
●O
A
归纳总结
切线的性质定理:
探索新知
当堂检测
1.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
A
当堂检测
2.经过☉O的直径的一端能作 条☉O的切线( )
A.0 B.1 C.2 D.3
B
C
当堂检测
4.如图所示,PA,PB是☉O的切线,A,B是切点,点C为☉O上一点,若∠P=40°,则∠ACB的度数为( )
A.70° B.50°
C.20° D.40°
A
当堂检测
5.已知☉O的半径是一元二次方程x2-5x-6=0的一个根,圆心O到直线l的距离d=4,则直线l与☉O的位置关系是( )
A.相交 B.相切
C.相离 D.平行
6.如图所示,过☉O外一点P作圆的切线PA,PB,
点A,B为切点,AC为直径,设∠P=m°,∠C=n°,
则m,n之间的数量关系为 .
A
m+2n=180
当堂检测
3
当堂检测
8.如图所示,BC是☉O的直径,CE是☉O的弦,过点E作☉O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.
(1)求证:∠ABG=2∠C;
(1)证明:如图所示,连接OE.
∵EG是☉O的切线,
∴OE⊥EG.
∵BF⊥GE,∴OE∥AB,∴∠A=∠OEC.
∵OE=OC,∴∠OEC=∠C,∴∠A=∠C.
∵∠ABG=∠A+∠C,∴∠ABG=2∠C.
当堂检测
直线和圆的位置关系及切线的性质
直线和圆的位置关系的性质
直线和圆的三种位置关系
相交:直线和圆有两个公共点
相切:直线和圆有一个公共点
相离:直线和圆没有公共点
(1) 直线和圆相交;d
(3) 直线和圆相离;d>r
切线的性质
圆的切线垂直于经过切点的半径.
感谢收看
