6.1 第1课时 平方根 课件(共28张PPT) ——沪科版(2024)七年级数学下册
文档属性
| 名称 | 6.1 第1课时 平方根 课件(共28张PPT) ——沪科版(2024)七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 10:24:21 | ||
图片预览





文档简介
(共28张PPT)
第一课时 平方根
6.1 平方根、立方根
学习目标及重难点
1.了解平方根、算术平方根的概念,会用根号表示一个数的平方根以及算术平方根;(重点)
2.会求一个正数的平方根、算术平方根;(重点)
3.会用计算器计算一个正数的算术平方根.(难点)
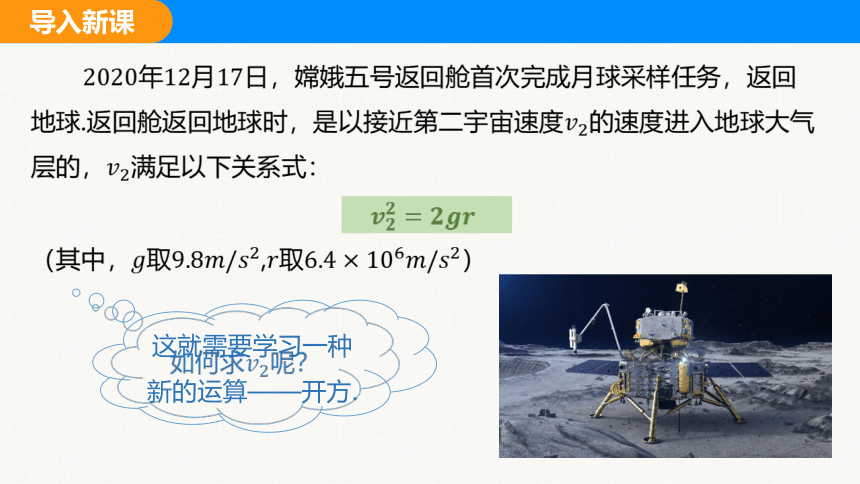
年月日,嫦娥五号返回舱首次完成月球采样任务,返回地球.返回舱返回地球时,是以接近第二宇宙速度的速度进入地球大气层的,满足以下关系式:
(其中,取,取)
如何求呢?
这就需要学习一种新的运算——开方.
探索1:平方根的概念及其性质
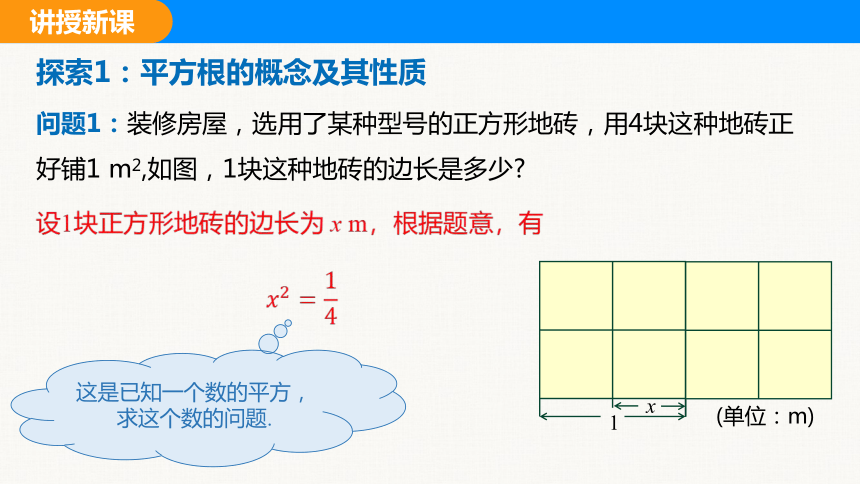
问题1:装修房屋,选用了某种型号的正方形地砖,用4块这种地砖正好铺1 m2,如图,1块这种地砖的边长是多少
设1块正方形地砖的边长为 x m,根据题意,有
1
x
(单位:m)
这是已知一个数的平方,求这个数的问题.
一般地,如果一个数的平方等于 , 那么这个数叫作的平方根,也叫作二次方根.
例如 : 因为,
所以的平方根是和(可以合写为).
换句话说,如果 ,那么叫作的平方根.
归纳总结
______和_______是的平方根,也就是说_____ 是16的平方根.
2. ,∴平方等于的数有_____个,它是______.
讨论:有没有一个数的平方等于?你能找到一个数的平方是负数吗?
不存在这样的数
随堂小练习
通过这些题目的解答,你能发现什么
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
平方根的性质:
归纳总结
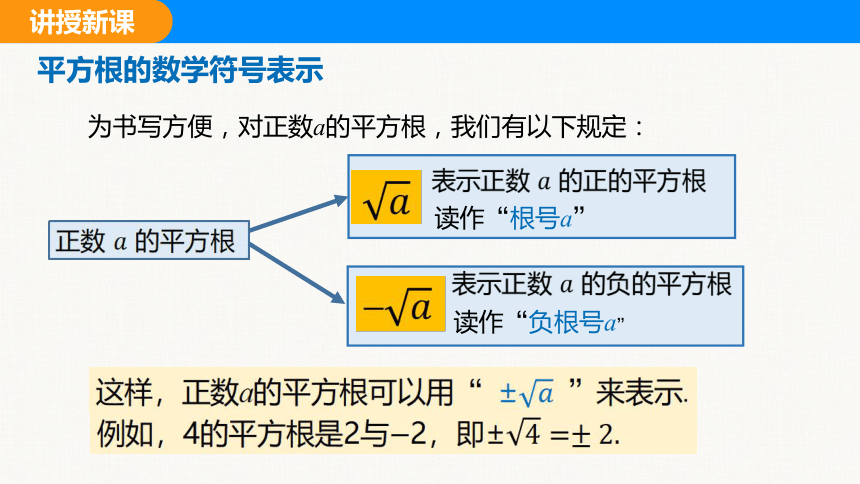
为书写方便,对正数a的平方根,我们有以下规定:
平方根的数学符号表示
这样,正数a的平方根可以用“ ± ”来表示.
正数 的平方根
表示正数 的正的平方根
表示正数 的负的平方根
读作“根号a”
读作“负根号a”
例如,4的平方根是2与2,即±
探索2:算术平方根的概念及性质
正数 的平方根
读作“根号a”
表示正数 的正的平方根
读作“负根号a”
表示正数 的负的平方根
这个根也叫作的算数平方根.
算术平方根具有双重非负性
a的算术平方根
算术平方根的性质
非负数
≥0
非负数
≥0
思考:你能总结一下平方根与算术平方根的概念的区别与联系吗?
区别:正数的平方根有两个,而它的算术平方根只有一个;
联系: 正数的两个平方根中正的那个平方根就是它的算术平方根,0的平方根就是它的算术平方根.
探索3:开平方根的概念
1
4
9
已知一个数,求它的平方的运算,叫做平方运算.
+1
1
+2
2
+3
3
平方
1
4
9
+1
1
+2
2
+3
3
反之,已知一个数的平方,求这个数的运算叫什么?
求一个数的平方根的运算叫作开平方.平方与开平方互为逆运算.
例1:求下列各数的平方根和算术平方根:
(1) ; (2) ; (3) ; (4) ( 3)
解:(1) 因为,所以的平方根是,即;的算术平方根是
解:(2) 因为,所以的平方根是,即 ;的算术平方根是.
解:(4) 因为,所以的平方根是,即 ; 的算术平方根是.
解:(3) 因为,所以的平方根是,即 ; 的算术平方根是.
例1:求下列各数的平方根和算术平方根:
(1) ; (2) ; (3) ; (4) ( 3)
判断正误:
(1)是的算术平方根.
(2) 是 的一个平方根.
(3)的平方根是.
(4)的算术平方根是.
随堂小练习
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数 的算术平方根(或其近似值).
a
=
按键顺序:
注意:计算器的型号不同,按键顺序可能有所不同,要注意阅读使用说明书.
探索4:用计算器求平方根
例2:用计算器求下列各式的值(精确到0.01):
(1) ; (2) ; (3) ; (4)
解:(1)在计算器上依次键入: ,显示结果是,精确到,得 1.41.
(2)
(3)
(4)在计算器上依次键入:
=
2
5
7
=
÷
即可得
第二宇宙速度是指使人造卫星脱离地球引力作用范围飞向太阳,并围绕太阳运动所需的最小发射速度.
用计算器可求得
年月日,嫦娥五号返回舱首次完成月球采样任务,返回地球.返回舱返回地球时,是以接近第二宇宙速度的速度进入地球大气层的,满足以下关系式:
(其中,取,取)
例3:如图,跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作,如果不考虑空气阻力等其他因素影响,弹跳到最高点后,人体下落到水面所需要的时间与下落的高度之间应遵循下面的公式:
其中的单位是,的单位是,,假设跳板的高度是,运动员在跳板上跳起至高出跳板处开始下落,那么运动员下落到水面约需多长时间?
解:设运动员下落到水面约需 s ,根据题意,得
,
因为所以
因而,运动员下落到水面约需s.
1. 9的平方根是( )
A.3 B.±3 C.-3 D.9
B
2. “36的平方根是±6”,用数学式子表示为( )
B
习题1
3. 下列说法中,正确的是( )
A.9的平方根是±3,应表示为92=±3
B.±3是9的平方根,应表示为± =3
C.把9开平方能得到9的平方根,即 =±3
D.9的算术平方根是3,应表示为 =3
D
习题2
4. (1)算术平方根等于它本身的数是______;
(2)_____的算术平方根等于它的相反数.
0和1
0
习题3
5.(1)若某个正数的一个平方根是,则它的另一个平方根是______.
(2)一个正数的平方根分别是和,则x=_____.
5
习题4
6.用计算器求下列各式的值(精确到0.01):
(1) ;(2) ; (3) ; (4) .
解:(1)
(2) ;
(3) ;
(4)
习题5
平方根
正数的平方根
0的平方根
算术平方根
正平方根
(就是0本身)
负数的平方根
双重非负性
负平方根
(没有)
第一课时 平方根
6.1 平方根、立方根
学习目标及重难点
1.了解平方根、算术平方根的概念,会用根号表示一个数的平方根以及算术平方根;(重点)
2.会求一个正数的平方根、算术平方根;(重点)
3.会用计算器计算一个正数的算术平方根.(难点)
年月日,嫦娥五号返回舱首次完成月球采样任务,返回地球.返回舱返回地球时,是以接近第二宇宙速度的速度进入地球大气层的,满足以下关系式:
(其中,取,取)
如何求呢?
这就需要学习一种新的运算——开方.
探索1:平方根的概念及其性质
问题1:装修房屋,选用了某种型号的正方形地砖,用4块这种地砖正好铺1 m2,如图,1块这种地砖的边长是多少
设1块正方形地砖的边长为 x m,根据题意,有
1
x
(单位:m)
这是已知一个数的平方,求这个数的问题.
一般地,如果一个数的平方等于 , 那么这个数叫作的平方根,也叫作二次方根.
例如 : 因为,
所以的平方根是和(可以合写为).
换句话说,如果 ,那么叫作的平方根.
归纳总结
______和_______是的平方根,也就是说_____ 是16的平方根.
2. ,∴平方等于的数有_____个,它是______.
讨论:有没有一个数的平方等于?你能找到一个数的平方是负数吗?
不存在这样的数
随堂小练习
通过这些题目的解答,你能发现什么
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
平方根的性质:
归纳总结
为书写方便,对正数a的平方根,我们有以下规定:
平方根的数学符号表示
这样,正数a的平方根可以用“ ± ”来表示.
正数 的平方根
表示正数 的正的平方根
表示正数 的负的平方根
读作“根号a”
读作“负根号a”
例如,4的平方根是2与2,即±
探索2:算术平方根的概念及性质
正数 的平方根
读作“根号a”
表示正数 的正的平方根
读作“负根号a”
表示正数 的负的平方根
这个根也叫作的算数平方根.
算术平方根具有双重非负性
a的算术平方根
算术平方根的性质
非负数
≥0
非负数
≥0
思考:你能总结一下平方根与算术平方根的概念的区别与联系吗?
区别:正数的平方根有两个,而它的算术平方根只有一个;
联系: 正数的两个平方根中正的那个平方根就是它的算术平方根,0的平方根就是它的算术平方根.
探索3:开平方根的概念
1
4
9
已知一个数,求它的平方的运算,叫做平方运算.
+1
1
+2
2
+3
3
平方
1
4
9
+1
1
+2
2
+3
3
反之,已知一个数的平方,求这个数的运算叫什么?
求一个数的平方根的运算叫作开平方.平方与开平方互为逆运算.
例1:求下列各数的平方根和算术平方根:
(1) ; (2) ; (3) ; (4) ( 3)
解:(1) 因为,所以的平方根是,即;的算术平方根是
解:(2) 因为,所以的平方根是,即 ;的算术平方根是.
解:(4) 因为,所以的平方根是,即 ; 的算术平方根是.
解:(3) 因为,所以的平方根是,即 ; 的算术平方根是.
例1:求下列各数的平方根和算术平方根:
(1) ; (2) ; (3) ; (4) ( 3)
判断正误:
(1)是的算术平方根.
(2) 是 的一个平方根.
(3)的平方根是.
(4)的算术平方根是.
随堂小练习
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数 的算术平方根(或其近似值).
a
=
按键顺序:
注意:计算器的型号不同,按键顺序可能有所不同,要注意阅读使用说明书.
探索4:用计算器求平方根
例2:用计算器求下列各式的值(精确到0.01):
(1) ; (2) ; (3) ; (4)
解:(1)在计算器上依次键入: ,显示结果是,精确到,得 1.41.
(2)
(3)
(4)在计算器上依次键入:
=
2
5
7
=
÷
即可得
第二宇宙速度是指使人造卫星脱离地球引力作用范围飞向太阳,并围绕太阳运动所需的最小发射速度.
用计算器可求得
年月日,嫦娥五号返回舱首次完成月球采样任务,返回地球.返回舱返回地球时,是以接近第二宇宙速度的速度进入地球大气层的,满足以下关系式:
(其中,取,取)
例3:如图,跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作,如果不考虑空气阻力等其他因素影响,弹跳到最高点后,人体下落到水面所需要的时间与下落的高度之间应遵循下面的公式:
其中的单位是,的单位是,,假设跳板的高度是,运动员在跳板上跳起至高出跳板处开始下落,那么运动员下落到水面约需多长时间?
解:设运动员下落到水面约需 s ,根据题意,得
,
因为所以
因而,运动员下落到水面约需s.
1. 9的平方根是( )
A.3 B.±3 C.-3 D.9
B
2. “36的平方根是±6”,用数学式子表示为( )
B
习题1
3. 下列说法中,正确的是( )
A.9的平方根是±3,应表示为92=±3
B.±3是9的平方根,应表示为± =3
C.把9开平方能得到9的平方根,即 =±3
D.9的算术平方根是3,应表示为 =3
D
习题2
4. (1)算术平方根等于它本身的数是______;
(2)_____的算术平方根等于它的相反数.
0和1
0
习题3
5.(1)若某个正数的一个平方根是,则它的另一个平方根是______.
(2)一个正数的平方根分别是和,则x=_____.
5
习题4
6.用计算器求下列各式的值(精确到0.01):
(1) ;(2) ; (3) ; (4) .
解:(1)
(2) ;
(3) ;
(4)
习题5
平方根
正数的平方根
0的平方根
算术平方根
正平方根
(就是0本身)
负数的平方根
双重非负性
负平方根
(没有)
