7.2 第3课时 一元一次不等式的应用 课件(共21张PPT)—— 沪科版(2024)七年级数学下册
文档属性
| 名称 | 7.2 第3课时 一元一次不等式的应用 课件(共21张PPT)—— 沪科版(2024)七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
7.2 一元一次不等式
第三课时 一元一次不等式的应用
学习目标及重难点
1.会通过列一元一次不等式去解决生活中的实际问题,经历“实际问题抽象为不等式模型”的过程;(重点)
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论思想在用不等式解决实际问题中的应用.
1.解不等式,并把解集在数轴上表示出来.
解:去分母,得
去括号,得
移项,得
合并同类项,得 .
这个不等式的解集在数轴上表示为:
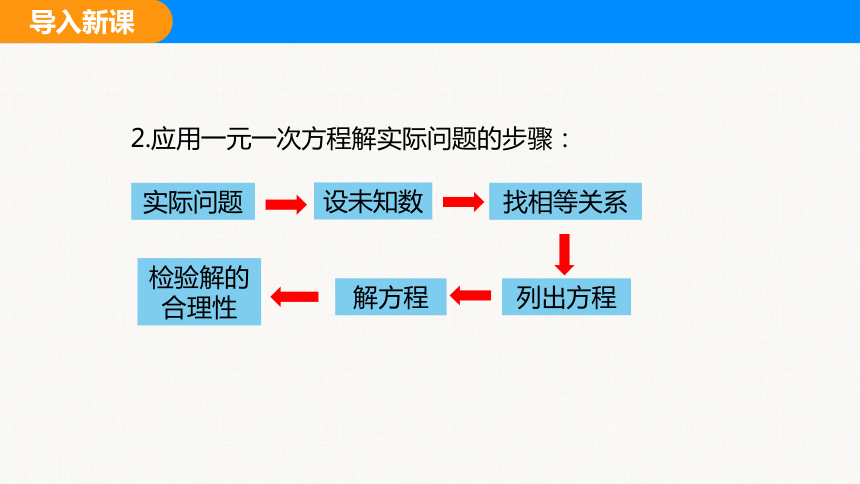
2.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
探索1:一元一次不等式的应用
例1:为拓宽农民增收致富渠道,某村依托自身油菜种植业优势,举办油菜花节,其间进行民俗表演,表演收取门票,个人票每张10元,20人以上(含20人)的团体票8折优惠.当人数不足20人的情况下,何时买20人的团体票比买个人票要便宜?
解:设人数为时,买个人票需要元,买20人的团体票需要元.根据题意,得
解不等式,得
因为人数必须是小于20的整数,即,
因此,当人数是时,买人的团体票比买个人票要便宜.
小王计划给灾区同学捐献一些笔和笔记本.已知每支笔的价格为3元,每本笔记本的价格为4元,小王在买了50支笔后准备把剩余的钱全部用来买笔记本,但他只有350元.问他最多能买多少本笔记本?
解:他最多能买本笔记本.
根据题意,得
解不等式,得
答:他最多能买50本笔记本.
随堂小练习
通过列一元一次不等式解决实际问题,你认为一般步骤是什么?
(1)审清题意;
(2)设未知数;
(3)由题意寻求不等关系,列出一元一次不等式;
(4)解一元一次不等式;
(5)根据实际情况,求出符合题意的解.
例2:去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少要增加多少?
上面问题中涉及的数量关系是
70%
解:设明年比去年空气质量良好的天数增加了x.去年有
365 60%天空气质量良好,明年有(x+365 60%)天空气质量良好,并且
移项,合并同类项,得 x>36.5.
答:明年空气质量良好的天数要比去年至少要增加37,才能使这一年空气质量良好的天数超过全年天数的70%.
×
×
去分母,得 x+219>255.5.
由x应为正整数,得 x≥37.
例3:甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家商场购物花费少?
分析:甲乙两商场的优惠价格不一样,因此需要分三种情况讨论.
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元;
(3)当购物超过100元.
解:(1)当累计购物不超过50元时,在甲、乙两商场都不享受优惠,因此到两商场购物花费一样;
(3)当累计购物超过100元时,设累计购物为x(x>100)元
①若到甲商场购物花费少,则
50+0.95(x-50)>100+0.9(x-100)
解得x>150
这就是说,累计购物超过150元时,在甲商场购物花费少;
(2)当累计购物超过50元而不超过100元时,在乙商场享受优惠,在甲商场不享受优惠,因此到乙商场购物花费少;
②若到乙商场购物花费少,则
50+0.95(x-50)<100+0.9(x-100)
解得x<150
这就是说,累计购物超过100元而不到150元时,在乙商场购物花费少;
③若50+0.95(x-50)=100+0.9(x-100)
解得x=150
这就是说,累计购物为150元时,在甲、乙两商场购物花费一样.
应用一元一次不等式解决实际问题的步骤:
找出不等关系
设未知数
实际问题
列不等式
解不等式
结合实际
确定答案
习题1
我市某初中举行了一次“八荣八耻”知识抢答竞赛,总共50道题.抢答规则:抢答对一题得3分,抢答错一题扣1分,不抢答得0分.小军同学参加了比赛,只抢答了其中的20道题,最后他的得分不少于50分,你知道小军至少答对几道题吗?
解:设小军至少答对x道题,则答错了(20-x)道题.
3x-(20-x) ≥50
解不等式,得
x≥17.5
因为x为正整数,所以x的最小正整数解为18.
答:小军至少答对了18道题.
根据题意,得
习题2
为了保护环境,某企业决定购买10台污水处理设备.现有A、B两种型号设备,其中A型号设备每台15万元,月处理污水250吨; B型号设备每台12万元,月处理污水220吨.经预算:该企业购买设备的资金不高于130万元.
(1)请你设计该企业的几种购买方案?
(2)若企业每月产生的污水量为2260吨,为了节约资金,应该选哪种购买方案?
解:(1)设购买污水处理设备A型x台,则B型(10-x)台.
根据题意,得
15x+12(10-x)≤130
解不等式,得
x ≤ 3.3
又因为x为非负整数,所以x可取0,1,2,3.
所以有四种购买方案:购A型0台,B型10台;购A型1台;B型9,购A型2台,B型8台;购A型3台,B型7台.
解:(2)方案一:
所耗资金为12×10=120(万元),月处理污水为220×10=2200(吨),2200<2260,舍去
方案二:
所耗资金为15+12×9=123(万元),月处理污水为250+220×9=2230(吨),2230<2260,舍去
方案三:
所耗资金为15×2+12×8=126(万元),
月处理污水为250×2+220×8=2260(吨).
方案四:
所耗资金为15×3+12×7=129(万元),
月处理污水为250×3+220×9=2290(吨).
因为126<129,所以为节约资金应选择方案三.
习题3
某校一名老师将在假期带领学生去北京旅游,有两种购票方式:甲旅行社说:“如果老师买全票,其他人全部半价优惠.”乙旅行社说:“所有人按全票价的6折优惠.”已知全票价240元.设学生有x名,甲旅行社的收费为y1元,乙旅行社的收费为y2元.
(1)分别表示两家旅行社的收费y1,y2与x的关系式;
(2)就学生人数讨论哪家旅行社更优惠.
解:(1)y1=240+240×50%×x=240+120x;
y2=240×60%×(x+1)=144(x+1)=144x+144.
(2)若y1=y2,则240+120x=144x+144,解得x=4,
此时两家旅行社收费一样;
若y1>y2,则240+120x>144x+144,解得x<4,
此时乙旅行社更优惠;
若y14,
此时甲旅行社更优惠.
根据实际问题找出符合条件的解集或整数解
解一元一次不等式
得出解决问题的答案
一元一次不等式的应用
实际问题
根据题意列不等式
7.2 一元一次不等式
第三课时 一元一次不等式的应用
学习目标及重难点
1.会通过列一元一次不等式去解决生活中的实际问题,经历“实际问题抽象为不等式模型”的过程;(重点)
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论思想在用不等式解决实际问题中的应用.
1.解不等式,并把解集在数轴上表示出来.
解:去分母,得
去括号,得
移项,得
合并同类项,得 .
这个不等式的解集在数轴上表示为:
2.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
探索1:一元一次不等式的应用
例1:为拓宽农民增收致富渠道,某村依托自身油菜种植业优势,举办油菜花节,其间进行民俗表演,表演收取门票,个人票每张10元,20人以上(含20人)的团体票8折优惠.当人数不足20人的情况下,何时买20人的团体票比买个人票要便宜?
解:设人数为时,买个人票需要元,买20人的团体票需要元.根据题意,得
解不等式,得
因为人数必须是小于20的整数,即,
因此,当人数是时,买人的团体票比买个人票要便宜.
小王计划给灾区同学捐献一些笔和笔记本.已知每支笔的价格为3元,每本笔记本的价格为4元,小王在买了50支笔后准备把剩余的钱全部用来买笔记本,但他只有350元.问他最多能买多少本笔记本?
解:他最多能买本笔记本.
根据题意,得
解不等式,得
答:他最多能买50本笔记本.
随堂小练习
通过列一元一次不等式解决实际问题,你认为一般步骤是什么?
(1)审清题意;
(2)设未知数;
(3)由题意寻求不等关系,列出一元一次不等式;
(4)解一元一次不等式;
(5)根据实际情况,求出符合题意的解.
例2:去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少要增加多少?
上面问题中涉及的数量关系是
70%
解:设明年比去年空气质量良好的天数增加了x.去年有
365 60%天空气质量良好,明年有(x+365 60%)天空气质量良好,并且
移项,合并同类项,得 x>36.5.
答:明年空气质量良好的天数要比去年至少要增加37,才能使这一年空气质量良好的天数超过全年天数的70%.
×
×
去分母,得 x+219>255.5.
由x应为正整数,得 x≥37.
例3:甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家商场购物花费少?
分析:甲乙两商场的优惠价格不一样,因此需要分三种情况讨论.
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元;
(3)当购物超过100元.
解:(1)当累计购物不超过50元时,在甲、乙两商场都不享受优惠,因此到两商场购物花费一样;
(3)当累计购物超过100元时,设累计购物为x(x>100)元
①若到甲商场购物花费少,则
50+0.95(x-50)>100+0.9(x-100)
解得x>150
这就是说,累计购物超过150元时,在甲商场购物花费少;
(2)当累计购物超过50元而不超过100元时,在乙商场享受优惠,在甲商场不享受优惠,因此到乙商场购物花费少;
②若到乙商场购物花费少,则
50+0.95(x-50)<100+0.9(x-100)
解得x<150
这就是说,累计购物超过100元而不到150元时,在乙商场购物花费少;
③若50+0.95(x-50)=100+0.9(x-100)
解得x=150
这就是说,累计购物为150元时,在甲、乙两商场购物花费一样.
应用一元一次不等式解决实际问题的步骤:
找出不等关系
设未知数
实际问题
列不等式
解不等式
结合实际
确定答案
习题1
我市某初中举行了一次“八荣八耻”知识抢答竞赛,总共50道题.抢答规则:抢答对一题得3分,抢答错一题扣1分,不抢答得0分.小军同学参加了比赛,只抢答了其中的20道题,最后他的得分不少于50分,你知道小军至少答对几道题吗?
解:设小军至少答对x道题,则答错了(20-x)道题.
3x-(20-x) ≥50
解不等式,得
x≥17.5
因为x为正整数,所以x的最小正整数解为18.
答:小军至少答对了18道题.
根据题意,得
习题2
为了保护环境,某企业决定购买10台污水处理设备.现有A、B两种型号设备,其中A型号设备每台15万元,月处理污水250吨; B型号设备每台12万元,月处理污水220吨.经预算:该企业购买设备的资金不高于130万元.
(1)请你设计该企业的几种购买方案?
(2)若企业每月产生的污水量为2260吨,为了节约资金,应该选哪种购买方案?
解:(1)设购买污水处理设备A型x台,则B型(10-x)台.
根据题意,得
15x+12(10-x)≤130
解不等式,得
x ≤ 3.3
又因为x为非负整数,所以x可取0,1,2,3.
所以有四种购买方案:购A型0台,B型10台;购A型1台;B型9,购A型2台,B型8台;购A型3台,B型7台.
解:(2)方案一:
所耗资金为12×10=120(万元),月处理污水为220×10=2200(吨),2200<2260,舍去
方案二:
所耗资金为15+12×9=123(万元),月处理污水为250+220×9=2230(吨),2230<2260,舍去
方案三:
所耗资金为15×2+12×8=126(万元),
月处理污水为250×2+220×8=2260(吨).
方案四:
所耗资金为15×3+12×7=129(万元),
月处理污水为250×3+220×9=2290(吨).
因为126<129,所以为节约资金应选择方案三.
习题3
某校一名老师将在假期带领学生去北京旅游,有两种购票方式:甲旅行社说:“如果老师买全票,其他人全部半价优惠.”乙旅行社说:“所有人按全票价的6折优惠.”已知全票价240元.设学生有x名,甲旅行社的收费为y1元,乙旅行社的收费为y2元.
(1)分别表示两家旅行社的收费y1,y2与x的关系式;
(2)就学生人数讨论哪家旅行社更优惠.
解:(1)y1=240+240×50%×x=240+120x;
y2=240×60%×(x+1)=144(x+1)=144x+144.
(2)若y1=y2,则240+120x=144x+144,解得x=4,
此时两家旅行社收费一样;
若y1>y2,则240+120x>144x+144,解得x<4,
此时乙旅行社更优惠;
若y1
此时甲旅行社更优惠.
根据实际问题找出符合条件的解集或整数解
解一元一次不等式
得出解决问题的答案
一元一次不等式的应用
实际问题
根据题意列不等式
