7.3 第2课时 解复杂的一元一次不等式组及不等式组的应用 课件(共28张PPT)——沪科版(2024)七年级数学下册
文档属性
| 名称 | 7.3 第2课时 解复杂的一元一次不等式组及不等式组的应用 课件(共28张PPT)——沪科版(2024)七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
7.3 一元一次不等式组
第二课时 解复杂的一元一次不等式组及不等式组的应用
学习目标及重难点
1.会解复杂的一元一次不等式组,并会在数轴上表示出来;(重点)
2.会通过列一元一次不等式组去解决生活中的实际问题.(重点、难点)
解:解不等式①,得
解不等式②,得
在数轴上分别表示这两个不等式的解集.
因此,原不等式组的解集为:
解不等式组:
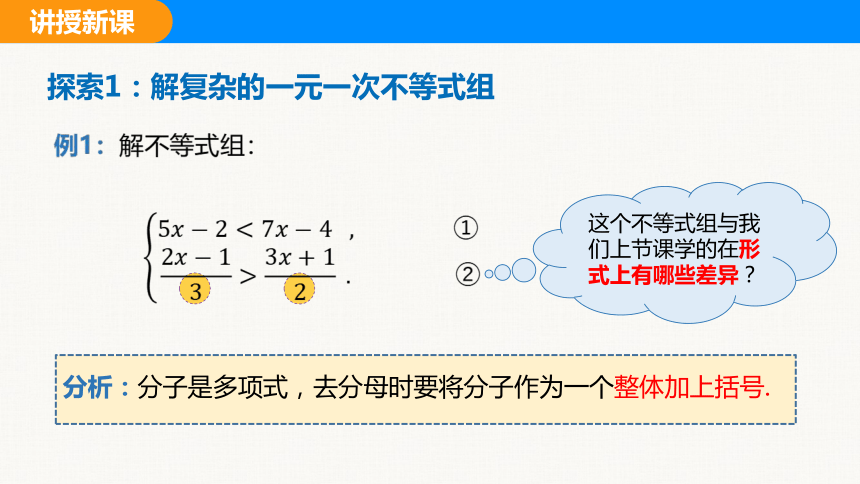
探索1:解复杂的一元一次不等式组
例1:解不等式组:
这个不等式组与我们上节课学的在形式上有哪些差异?
分析:分子是多项式,去分母时要将分子作为一个整体加上括号.
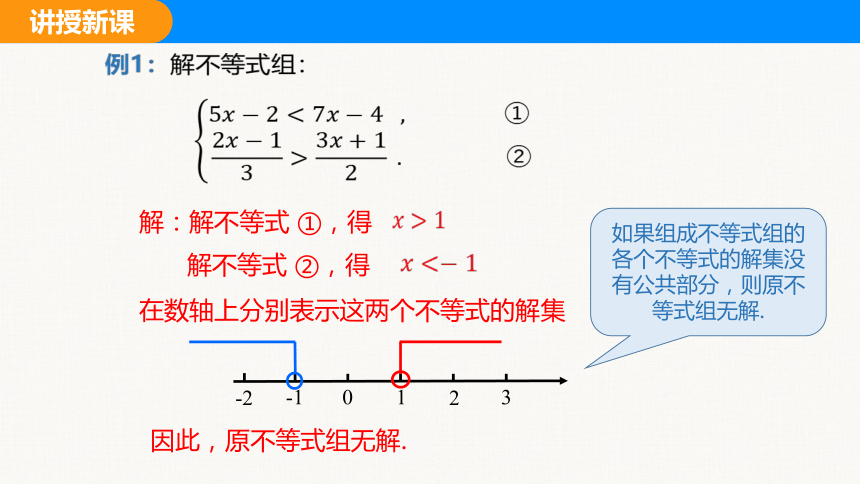
解:解不等式 ①,得
解不等式 ②,得
因此,原不等式组无解.
如果组成不等式组的各个不等式的解集没有公共部分,则原不等式组无解.
在数轴上分别表示这两个不等式的解集
-2
-1
0
1
2
3
例1:解不等式组:
探究:1.你是不是已经明白解一元一次不等式组的基本方法了呢?
接下来请你试一试吧,求下列不等式组的解集.
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
.
(1)
(2)
解: 原不等式组的解集为:
解: 原不等式组的解集为:
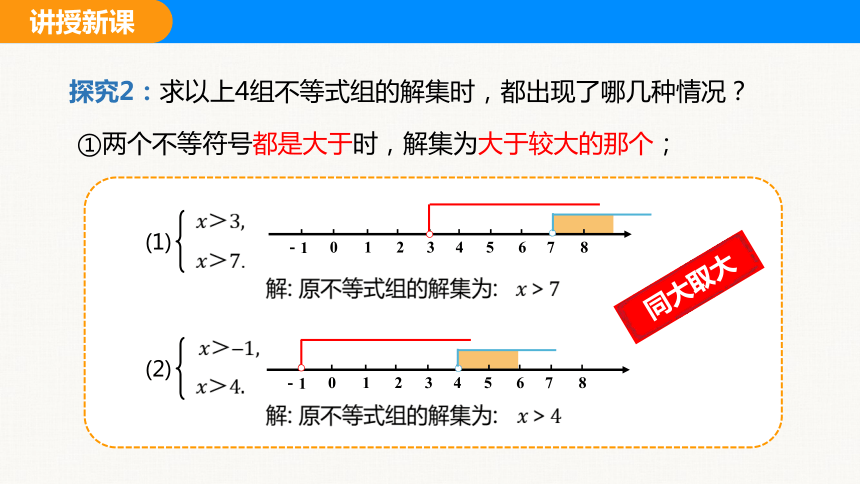
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
①两个不等符号都是大于时,解集为大于较大的那个;
同大取大
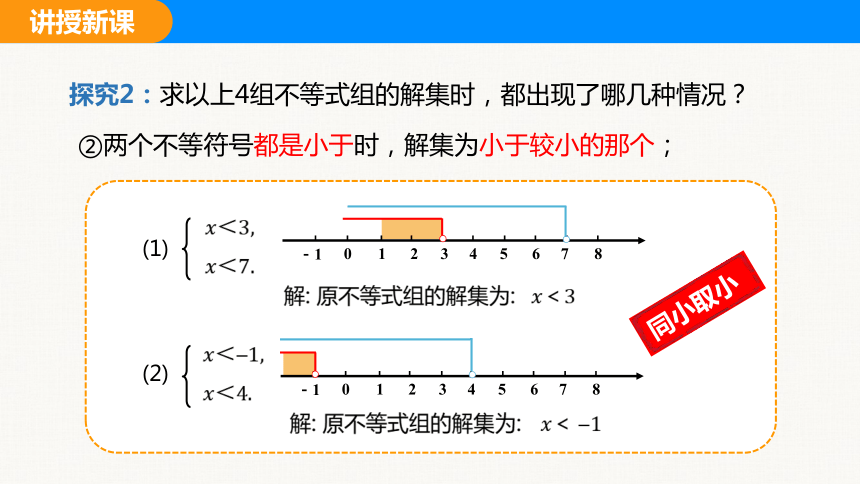
②两个不等符号都是小于时,解集为小于较小的那个;
(1)
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
(2)
解: 原不等式组的解集为:
解: 原不等式组的解集为:
同小取小
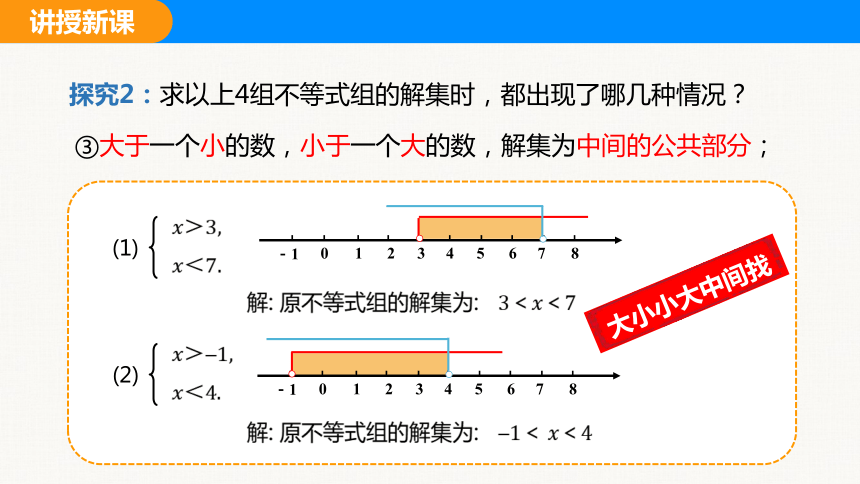
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
③大于一个小的数,小于一个大的数,解集为中间的公共部分;
(1)
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
(2)
解: 原不等式组的解集为:
解: 原不等式组的解集为:
大小小大中间找
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
④大于一个大的数,小于一个小的数,不等式组无解.
(1)
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
(2)
解: 原不等式组:无解
解: 原不等式组:无解
大大小小无处找
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
.
(1)
(2)
(3)
(4)
a b
同 大 取 大
a b
同 小 取 小
a b
大小小大中间找
a b
大大小小无处找
无解
交流:假设,你能很快说出下列不等式组的解集吗?
利用口诀法求出下列不等式组的解集.
(1)
(3)
(4)
(2)
同大取大;
同小取小;
大小小大中间找;
大大小小无处找.
无解
随堂小练习
确定一元一次不等式组解集的常用方法
(1)数轴法:运用数轴法确定不等式组的解集,就是将不等式组中的每一个不等式的解集在数轴上表示出来,然后找出它们的公共部分,这个公共部分就是此不等式组的解集.若没有公共部分,则这个不等式组无解.这种方法体现了数形结合的思想,既直观又明了.
(2)口诀法:求不等式组的解集时,可记住前面的规律:同大取大,同小取小,大小小大中间找,大大小小无处找.
探索2:一元一次不等式组的应用
例2:3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
(2)“提前完成任务”是什么意思?
提高生产速度后,10天的产品数量大于500
(3)根据这两句话你能列出不等式组解决这个实际问题吗?
学生独立探索以下问题:
(1)“不能完成任务”是什么意思?
按原先的生产速度,10天的产品数量小于500
解:设每个小组原先每天生产x件产品.
解得
因为x为正整数,
答:每个小组原先每天生产16件产品.
所以x为16.
3×10x<500
3×10(x+1)>500
①
②
15根据题意,得
例3:某中学为八年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数.
解:设宿舍间数为x间.根据题意,得
8(x-1)<4x+20
8x>4x+20
①
②
解得
5<x<7
因为x为正整数,所以x为6.
所以学生数为 4x+20=4×6+20=44 (人)
答:宿舍间数为6间,寄宿学生有44人.
列一元一次不等式组解实际问题的一般步骤:
(1)审清题意;
(2)设未知数;
(3)由题意寻求不等关系,列出一元一次不等式组;
(4)解一元一次不等式组;
(5)根据实际情况,求出符合题意的解.
例4:已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x-a<1
x-2b>3a
解: 由不等式组得
x <
x >3a+2b
因为不等式组的解集为 -1< x < 1 ,
所以
=1
3a+2b= -1
解得 a=1 , b= - 2
所以 (a+1)(b-1)=2×(-3)=-6.
1.解不等式组,并把解集在数轴上表示出来.
解:
解不等式②,得.
因此,原不等式组无解.
解不等式①,得 .
①
②
0
8
习题1
2.求满足下面不等式组中整数的最大值和最小值.
解:
解不等式①,得
,
.
①
②
解不等式②,得
∴不等式组的解集为
∴整数的最大值是 ,最小值是
习题2
3.求不等式组 的整数解.
解:
注意:
是一元一次不等式组,是 的另一种表示形式.
由题意可得不等式组
,
.
①
②
解不等式①,得
解不等式②,得.
∴该不等式组的解集为.
∴不等式组的整数解为
习题3
4.某工厂工人经过第一次改进工作方法,每人每天平均加工的零件比原来多10个,因而,每人在8天内加工的零件超过200个,第二次又改进工作方法,每人每天平均又比第一次改进方法后多做27个零件,这样只做了4天,所做的件数就超过前8天所做的数量.试问每个工人原来每人平均做几个零件?
习题4
解:设每个工人原来每天平均做x个零件.
解得 15<x<17
因为x为正整数,所以x为16.
答:每个工人原来每天平均做16个零件.
8(x+10)>200
4(x+10+27)>8(x+10)
①
②
根据题意,得
习题4
5.某公司经营甲、乙两种商品,每件甲种商品进价12万元,售价14.5万元.每件乙种商品进价8万元,售价10万元,且它们的进价和售价始终不变.现准备购进甲、乙两种商品共20件,所用资金不低于190万元不高于200万元.
习题5
(1)该公司有哪几种进货方案?
解:设购进甲种商品x件,则乙种(20-x)件.根据题意,得
12x+8(20-x)≥190
12x+8(20-x)≤200
①
②
解得 7.5≤x≤10
因为x为正整数,所以x为8、9、10.
所以有三种方案:方案一 ,购买甲8件,乙12件;方案二,购买甲9件,乙11件;方案三,购买甲10件,乙10件.
习题5
(2)该公司采用哪种进货方案可获得最大利润?最大利润是多少?
解:方案一
8(14.5-12)+12(10-8)=44(万元)
方案二
9(14.5-12)+11(10-8)=44.5(万元)
方案三
10(14.5-12)+10(10-8)=45(万元)
所以方案三获利最大,最大利润为45万元.
因为44<44.5<45
习题5
解较复杂的一元一次不等式组
一元一次不等式组
实际应用(整数解)
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
7.3 一元一次不等式组
第二课时 解复杂的一元一次不等式组及不等式组的应用
学习目标及重难点
1.会解复杂的一元一次不等式组,并会在数轴上表示出来;(重点)
2.会通过列一元一次不等式组去解决生活中的实际问题.(重点、难点)
解:解不等式①,得
解不等式②,得
在数轴上分别表示这两个不等式的解集.
因此,原不等式组的解集为:
解不等式组:
探索1:解复杂的一元一次不等式组
例1:解不等式组:
这个不等式组与我们上节课学的在形式上有哪些差异?
分析:分子是多项式,去分母时要将分子作为一个整体加上括号.
解:解不等式 ①,得
解不等式 ②,得
因此,原不等式组无解.
如果组成不等式组的各个不等式的解集没有公共部分,则原不等式组无解.
在数轴上分别表示这两个不等式的解集
-2
-1
0
1
2
3
例1:解不等式组:
探究:1.你是不是已经明白解一元一次不等式组的基本方法了呢?
接下来请你试一试吧,求下列不等式组的解集.
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
.
(1)
(2)
解: 原不等式组的解集为:
解: 原不等式组的解集为:
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
①两个不等符号都是大于时,解集为大于较大的那个;
同大取大
②两个不等符号都是小于时,解集为小于较小的那个;
(1)
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
(2)
解: 原不等式组的解集为:
解: 原不等式组的解集为:
同小取小
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
③大于一个小的数,小于一个大的数,解集为中间的公共部分;
(1)
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
(2)
解: 原不等式组的解集为:
解: 原不等式组的解集为:
大小小大中间找
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
④大于一个大的数,小于一个小的数,不等式组无解.
(1)
0
1
2
3
-1
4
5
6
7
8
0
1
2
3
-1
4
5
6
7
8
(2)
解: 原不等式组:无解
解: 原不等式组:无解
大大小小无处找
探究2:求以上4组不等式组的解集时,都出现了哪几种情况?
.
(1)
(2)
(3)
(4)
a b
同 大 取 大
a b
同 小 取 小
a b
大小小大中间找
a b
大大小小无处找
无解
交流:假设,你能很快说出下列不等式组的解集吗?
利用口诀法求出下列不等式组的解集.
(1)
(3)
(4)
(2)
同大取大;
同小取小;
大小小大中间找;
大大小小无处找.
无解
随堂小练习
确定一元一次不等式组解集的常用方法
(1)数轴法:运用数轴法确定不等式组的解集,就是将不等式组中的每一个不等式的解集在数轴上表示出来,然后找出它们的公共部分,这个公共部分就是此不等式组的解集.若没有公共部分,则这个不等式组无解.这种方法体现了数形结合的思想,既直观又明了.
(2)口诀法:求不等式组的解集时,可记住前面的规律:同大取大,同小取小,大小小大中间找,大大小小无处找.
探索2:一元一次不等式组的应用
例2:3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
(2)“提前完成任务”是什么意思?
提高生产速度后,10天的产品数量大于500
(3)根据这两句话你能列出不等式组解决这个实际问题吗?
学生独立探索以下问题:
(1)“不能完成任务”是什么意思?
按原先的生产速度,10天的产品数量小于500
解:设每个小组原先每天生产x件产品.
解得
因为x为正整数,
答:每个小组原先每天生产16件产品.
所以x为16.
3×10x<500
3×10(x+1)>500
①
②
15
例3:某中学为八年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数.
解:设宿舍间数为x间.根据题意,得
8(x-1)<4x+20
8x>4x+20
①
②
解得
5<x<7
因为x为正整数,所以x为6.
所以学生数为 4x+20=4×6+20=44 (人)
答:宿舍间数为6间,寄宿学生有44人.
列一元一次不等式组解实际问题的一般步骤:
(1)审清题意;
(2)设未知数;
(3)由题意寻求不等关系,列出一元一次不等式组;
(4)解一元一次不等式组;
(5)根据实际情况,求出符合题意的解.
例4:已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x-a<1
x-2b>3a
解: 由不等式组得
x <
x >3a+2b
因为不等式组的解集为 -1< x < 1 ,
所以
=1
3a+2b= -1
解得 a=1 , b= - 2
所以 (a+1)(b-1)=2×(-3)=-6.
1.解不等式组,并把解集在数轴上表示出来.
解:
解不等式②,得.
因此,原不等式组无解.
解不等式①,得 .
①
②
0
8
习题1
2.求满足下面不等式组中整数的最大值和最小值.
解:
解不等式①,得
,
.
①
②
解不等式②,得
∴不等式组的解集为
∴整数的最大值是 ,最小值是
习题2
3.求不等式组 的整数解.
解:
注意:
是一元一次不等式组,是 的另一种表示形式.
由题意可得不等式组
,
.
①
②
解不等式①,得
解不等式②,得.
∴该不等式组的解集为.
∴不等式组的整数解为
习题3
4.某工厂工人经过第一次改进工作方法,每人每天平均加工的零件比原来多10个,因而,每人在8天内加工的零件超过200个,第二次又改进工作方法,每人每天平均又比第一次改进方法后多做27个零件,这样只做了4天,所做的件数就超过前8天所做的数量.试问每个工人原来每人平均做几个零件?
习题4
解:设每个工人原来每天平均做x个零件.
解得 15<x<17
因为x为正整数,所以x为16.
答:每个工人原来每天平均做16个零件.
8(x+10)>200
4(x+10+27)>8(x+10)
①
②
根据题意,得
习题4
5.某公司经营甲、乙两种商品,每件甲种商品进价12万元,售价14.5万元.每件乙种商品进价8万元,售价10万元,且它们的进价和售价始终不变.现准备购进甲、乙两种商品共20件,所用资金不低于190万元不高于200万元.
习题5
(1)该公司有哪几种进货方案?
解:设购进甲种商品x件,则乙种(20-x)件.根据题意,得
12x+8(20-x)≥190
12x+8(20-x)≤200
①
②
解得 7.5≤x≤10
因为x为正整数,所以x为8、9、10.
所以有三种方案:方案一 ,购买甲8件,乙12件;方案二,购买甲9件,乙11件;方案三,购买甲10件,乙10件.
习题5
(2)该公司采用哪种进货方案可获得最大利润?最大利润是多少?
解:方案一
8(14.5-12)+12(10-8)=44(万元)
方案二
9(14.5-12)+11(10-8)=44.5(万元)
方案三
10(14.5-12)+10(10-8)=45(万元)
所以方案三获利最大,最大利润为45万元.
因为44<44.5<45
习题5
解较复杂的一元一次不等式组
一元一次不等式组
实际应用(整数解)
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
