华师大版七下(2024版)8.1.2三角形的内角和与外角和 教案
文档属性
| 名称 | 华师大版七下(2024版)8.1.2三角形的内角和与外角和 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1005.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:56:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
分课时教学设计
《8.1.2三角形的内角和与外角和》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 小学阶段已经了解了“三角形的内角和等于180°”,教材又将学生熟悉的知识点安排在此处,不是为了让学生做简单的回顾,主要的是要让学生学习用演绎推理的方法证明这个结论.并在这个结论的基础上推出:直角三角形的两个锐角互余;三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,最后再给出“三角形的外角和等于360°”的结论,作为对后面探索多边形的外角和定理的铺垫.这部分内容是让学生进行演绎推理很好的素材,并且让学生体会到数学证明的必要性.
学习者分析 本节课是在学生学行线的性质及三角形有关的概念,边、角之间关系的基础上,让学生动手操作,通过剪拼的实验与操作,提高学生动手能力;经历三角形内角和外角关系的探究过程,在探究中发展合情推理的能力;使学生学会探索数学问题的归纳法和实验法等研究方法。
教学目标 1.让学生在操作活动中,探索并了解三角形的内角和、三角形的外角的两条性质以及三角形的外角和. 2.利用平行线性质来证明三角形的内角和、三角形的外角的第一个性质以及三角形的外角和. 3.会利用“三角形的一个外角等于与它不相邻的两个内角的和”进行有关计算.
教学重点 掌握三角形的内角和、三角形的外角的两条性质以及三角形的外角和,并能利用三角形内角和、外角和以及外角的两条性质进行有关计算.
教学难点 在三角形内角和、三角形的外角的两条性质以及三角形的外角和证明的过程中,涉及到添加辅助线来沟通证明思路的方法.
学习活动设计
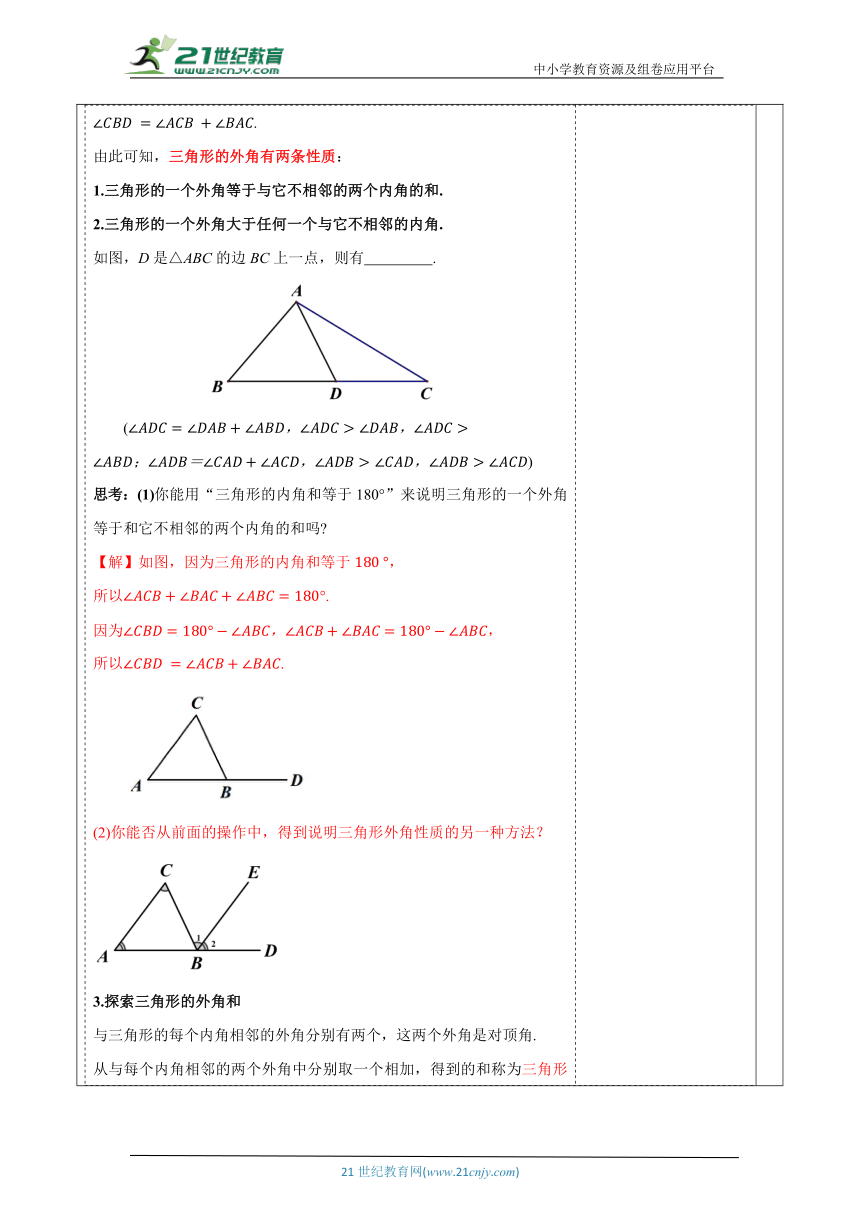
教师活动学生活动环节一:情境导入教师活动1: 如图 , 在小学我们曾剪下三角形的两个内角, 将它们与第三个内角拼在一起, 发现三个内角恰好拼成一个平角, 得出了如下结论: 三角形的内角和等于 . 如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?学生活动1: 通过探究活动理解.学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知.激发学生继续探究三角形内角和和外角和的兴趣。 活动意图说明: 从实际出发,从学生已有的生活经验出发.了解“三角形的内角和等于180°”,更主要的是要让学生学习用演绎推理的方法证明这个结论.环节二:新知探究教师活动2: 1.三角形的内角和定理的推理证明. 如图,已知 ,分别用,,表示的三个内角,证明. 【解】如图,延长到,以点为顶点,在的上侧作,则(同位角相等,两直线平行). , (两直线平行,内错角相等). 又, (等量代换). 思考:多种方法说明三角形内角和等于180°的核心是什么? 总结:1.在这里,为了需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线. 2.为了说明三角形三个内角的和为180°,常将三个角转化为一个平角,这种转化思想是数学中常用的方法. 思考:如图 , 在直角三角形中, ,与有什么关系 由于三角形的内角和等于,得 . , 由此可以推出 . 即与互余. 这就是说,直角三角形的两个锐角互余。 直角三角形可以用符号 “”表示,直角三角 形可以写成 . 思考:我们已经知道,直角三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗 有两个角互余的三角形是直角三角形. 思考:你能说明其理由吗? 2.探索三角形的外角及外角和. 如图, 一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角. 思考:三角形的外角与内角有什么关系呢 在图中, 显然有(外角) +(相邻的内角) . 思考:那么外角与其他两个不相邻的内角又有什么关系呢 依据三角形的内角和等于, 我们有. 由上面两个式子,可以推出 , . 因而可以得到你与你的同伴所发现的结论: . 由此可知,三角形的外角有两条性质: 1.三角形的一个外角等于与它不相邻的两个内角的和. 2.三角形的一个外角大于任何一个与它不相邻的内角. 如图,D是△ABC的边BC上一点,则有 . () 思考:(1)你能用“三角形的内角和等于180°”来说明三角形的一个外角等于和它不相邻的两个内角的和吗 【解】如图,因为三角形的内角和等于, 所以°. 因为, 所以. (2)你能否从前面的操作中,得到说明三角形外角性质的另一种方法? 3.探索三角形的外角和 与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角. 从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和. 如图所示,就是的外角和. 做一做:在图中, _______,_______, _______. 三式相加可以得到 _______+_______+_______=_______① 而,② 将①与②相比较,你能得出什么结论 概括: 可以得到. 由此可知:三角形的外角和等于360°. 思考:你能由下图说明这一结论吗? 解:因为, 所以,(两直线平行,同位角相等). 因为, 所以(等量代换).学生活动2: 学生可相互交流,学生自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论.理解三角形的外角的两条性质以及三角形的内角和与外角和.活动意图说明:引导学生建立模型,鼓励学生大胆探索,经历三角形内角和外角关系的探究过程,在探究中发展合情推理的能力.使学生学会探索数学问题的归纳法和实验法等研究方法.积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1 如图, 是的边上的高,, . 求的度数. 解 在中, (直角三角形的两个锐角互余), (等式性质) . 又(已知), (等量代换) . 在中, (三角形的内角和等于 180°), (等式性质) . 又 (已求), (已知), (等量代换) . 例2如图,是的 边上一点,,,. 求:(1)的度数; (2)的度数. 【分析】(1)先由三角形外角的性质得出,再由,即可得出的度数;(2)直接根据三角形的内角和定理得出的度数. 【解】(1) 是的外角(已知), (三角形的一个外角等于与它不相邻的两个内角的和). 又(已知), (等量代换). (2)(三角形的内角和等于), . . (等式的性质).学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 活动意图说明: 让学生在一定的数学活动中去体验、感受数学,掌握三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,三角形的外角和等于360°.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 8.1 三角形 8.1.2 三角形的内角和与外角和 1.三角形的内角和定理及推理证明. 2.三角形的外角及外角和. 3.探索证明“三角形的一个外角等于和它不相邻的两个内角的和”的方法. 4.探索三角形的外角和. 例1 例2
课堂练习 【知识技能类作业】 必做题: 1.将一块含有角的直角三角板和一把直尺按如图所示的方式摆放,若,则∠2的度数是( ) A. B. C. D. 2.小明观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知,,则的度数是( ) A. B. C. D. 3.如图是某款婴儿手推车的平面示意图,若,,,则的度数为( ) A. B. C. D. 选做题: 4.已知一张三角形纸片(如图甲),其中.将纸片沿过点的直线折叠,使点落到边上的点处,折痕为(如图乙).再将纸片沿过点的直线折叠,使点恰好与点重合,折痕为(如图丙).原三角形纸片中,的大小为( ) A. B. C. D. 5.把一块直尺与一块三角板如图放置,若,则的度数为 . 6.在中,,射线平分,P为边上一点,,垂足为O,则的度数为 . 【综合拓展类作业】 7.如图,AD为△ABC的中线,BE为△ABD的中线. (1)∠ABE=15°,∠BAD=40°,求∠BED的度数; (2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少 答案: 1.B 2.D 3.D 4.C 5.【答案】 【知识点】三角形的外角性质;同位角的概念 6.【答案】或 【知识点】三角形内角和定理;三角形的外角性质 7.【答案】(1)解:∵∠BED是△ABE的角∴∠BED=∠ABE+∠BAD又∴∠ABE=15°∠BAD=40° ∴∠BED=55° (2)△BDE的面积=40×=10,所以E到BC边的距离 =10÷÷5=8.
作业设计 【知识技能类作业】 必做题: 1.已知三角形一个内角的度数为70°,则x+y的值为( ) A.180 B.110 C.100 D.70 2.在△ABC中,∠A=10°,∠B=60°,则△ABC的形状是( ) A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形 3.物理课上,小明研究一个小木块沿斜坡向下滑动时的运动状态,如图,∠C=90°,∠B=13°,小木块(△DEF)在AB上,且EF∥AC,则∠DFE的度数为( ) A.13° B.77° C.87° D.63° 选做题: 4.如果将一副三角板按如图所示的方式叠放,那么∠α的度数是( ) A.75° B.100° C.105° D.135° 5.如图,AD平分∠BAC,∠B=35°,∠ADC=82°,则∠C= °. 6.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=36°,∠E=24°,则∠BAC= °. 【综合拓展类作业】 7.实验证明平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 阅读以上材料并解决下列问题. (1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,求∠2及∠3的度数. 解:易知∠1=∠4,∠5=∠6,∴∠7=180°-∠1-∠4= ,∵m∥n, ∴∠2+∠7=180°,∴∠2=180°-∠7= ,∴∠5=∠6= ,根据三角形内角和为180°,知∠3=180°-∠4-∠5= . 在(1)中,①若∠1=55°,则∠3= ;②若∠1=40°,则 ∠3= . (3)由(1)(2),请你猜想:当两平面镜a、b的夹角∠3为多少度时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行 请你写出推理过程. 答案: 1.B 由题图可知,x+y=180-70=110.故选B. 2.A ∵∠A=10°,∠B=60°,∴∠C=180°-∠A-∠B=180°-10°-60°=110°,∴△ABC是钝角三角形.故选A. 3.B ∵∠C=90°,∠B=13°,∴∠A=180°-∠C-∠B=77°,∵EF∥AC,∴∠DFE=∠A=77°.故选B. 4.C 解法一:如图,由题意可得∠1=30°,则∠2=45°-∠1=45°-30°=15°,∴∠α=90°+∠2=105°.故选C. 解法二:如上图,∵∠1=30°,∴∠3=180°-(30°+45°)=105°, ∴∠α=∠3=105°.故选C. 5.51 解析 ∵∠ADC是△ABD的外角,∴∠BAD=∠ADC-∠B=82°-35°=47°,∵AD平分∠BAC,∴∠BAC=2∠BAD=94°, ∴∠C=180°-∠B-∠BAC=51°. 6.84 解析 ∵∠B=36°,∠E=24°,∴∠ECD=∠B+∠E=36°+24°=60°. ∵CE为∠ACD的平分线,∴∠ACD=2∠ECD=120°.又∵∠ACD=∠B+∠BAC,∴∠BAC=∠ACD-∠B=120°-36°=84°. 7.解析 (1)80°;100°;40°;90°. (2)①∵∠1=55°,∴∠4=∠1=55°,∴∠7=180°-(∠1+∠4)=180°-110°=70°.∵m∥n,∴∠2=180°-∠7=180°-70°=110°.∵∠5=∠6,∴∠5=(180°-∠2)=×70°=35°.又∵∠3+∠4+∠5=180°, ∴∠3=180°-∠4-∠5=180°-55°-35°=90°. ②∵∠1=40°,∴∠4=∠1=40°,∴∠7=180°-(∠1+∠4)=180°-80°=100°.∵m∥n,∴∠2=180°-∠7=180°-100°=80°.∵∠5=∠6,∴∠5=(180°-∠2)=×100°=50°.又∵∠3+∠4+∠5=180°, ∴∠3=180°-∠4-∠5=180°-40°-50°=90°. (3)根据平面镜反射光线的规律可知,∠1=∠4,∠5=∠6,∵m∥n,∴∠2+∠7=180°,∵∠1+∠4+∠7=180°,∠2+∠5+∠6=180°,∴2(∠5+∠4)+(∠2+∠7)=360°,∴∠5+∠4=×(360°-180°)=90°.∵∠3+∠4+∠5=180°,∴∠3=180°-(∠4+∠5)=180°-90°=90°, ∴当∠3=90°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.
教学反思 三角形的内角和外角的性质反映了三角形的内角和外角是互相联系与制约的,我们可以用它来求三角形的内角或外角.解题时,有时还需添加辅助线,有时结合代数,用方程来解比较方便.
21世纪教育网(www.21cnjy.com)
分课时教学设计
《8.1.2三角形的内角和与外角和》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 小学阶段已经了解了“三角形的内角和等于180°”,教材又将学生熟悉的知识点安排在此处,不是为了让学生做简单的回顾,主要的是要让学生学习用演绎推理的方法证明这个结论.并在这个结论的基础上推出:直角三角形的两个锐角互余;三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,最后再给出“三角形的外角和等于360°”的结论,作为对后面探索多边形的外角和定理的铺垫.这部分内容是让学生进行演绎推理很好的素材,并且让学生体会到数学证明的必要性.
学习者分析 本节课是在学生学行线的性质及三角形有关的概念,边、角之间关系的基础上,让学生动手操作,通过剪拼的实验与操作,提高学生动手能力;经历三角形内角和外角关系的探究过程,在探究中发展合情推理的能力;使学生学会探索数学问题的归纳法和实验法等研究方法。
教学目标 1.让学生在操作活动中,探索并了解三角形的内角和、三角形的外角的两条性质以及三角形的外角和. 2.利用平行线性质来证明三角形的内角和、三角形的外角的第一个性质以及三角形的外角和. 3.会利用“三角形的一个外角等于与它不相邻的两个内角的和”进行有关计算.
教学重点 掌握三角形的内角和、三角形的外角的两条性质以及三角形的外角和,并能利用三角形内角和、外角和以及外角的两条性质进行有关计算.
教学难点 在三角形内角和、三角形的外角的两条性质以及三角形的外角和证明的过程中,涉及到添加辅助线来沟通证明思路的方法.
学习活动设计
教师活动学生活动环节一:情境导入教师活动1: 如图 , 在小学我们曾剪下三角形的两个内角, 将它们与第三个内角拼在一起, 发现三个内角恰好拼成一个平角, 得出了如下结论: 三角形的内角和等于 . 如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?学生活动1: 通过探究活动理解.学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知.激发学生继续探究三角形内角和和外角和的兴趣。 活动意图说明: 从实际出发,从学生已有的生活经验出发.了解“三角形的内角和等于180°”,更主要的是要让学生学习用演绎推理的方法证明这个结论.环节二:新知探究教师活动2: 1.三角形的内角和定理的推理证明. 如图,已知 ,分别用,,表示的三个内角,证明. 【解】如图,延长到,以点为顶点,在的上侧作,则(同位角相等,两直线平行). , (两直线平行,内错角相等). 又, (等量代换). 思考:多种方法说明三角形内角和等于180°的核心是什么? 总结:1.在这里,为了需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线. 2.为了说明三角形三个内角的和为180°,常将三个角转化为一个平角,这种转化思想是数学中常用的方法. 思考:如图 , 在直角三角形中, ,与有什么关系 由于三角形的内角和等于,得 . , 由此可以推出 . 即与互余. 这就是说,直角三角形的两个锐角互余。 直角三角形可以用符号 “”表示,直角三角 形可以写成 . 思考:我们已经知道,直角三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗 有两个角互余的三角形是直角三角形. 思考:你能说明其理由吗? 2.探索三角形的外角及外角和. 如图, 一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角. 思考:三角形的外角与内角有什么关系呢 在图中, 显然有(外角) +(相邻的内角) . 思考:那么外角与其他两个不相邻的内角又有什么关系呢 依据三角形的内角和等于, 我们有. 由上面两个式子,可以推出 , . 因而可以得到你与你的同伴所发现的结论: . 由此可知,三角形的外角有两条性质: 1.三角形的一个外角等于与它不相邻的两个内角的和. 2.三角形的一个外角大于任何一个与它不相邻的内角. 如图,D是△ABC的边BC上一点,则有 . () 思考:(1)你能用“三角形的内角和等于180°”来说明三角形的一个外角等于和它不相邻的两个内角的和吗 【解】如图,因为三角形的内角和等于, 所以°. 因为, 所以. (2)你能否从前面的操作中,得到说明三角形外角性质的另一种方法? 3.探索三角形的外角和 与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角. 从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和. 如图所示,就是的外角和. 做一做:在图中, _______,_______, _______. 三式相加可以得到 _______+_______+_______=_______① 而,② 将①与②相比较,你能得出什么结论 概括: 可以得到. 由此可知:三角形的外角和等于360°. 思考:你能由下图说明这一结论吗? 解:因为, 所以,(两直线平行,同位角相等). 因为, 所以(等量代换).学生活动2: 学生可相互交流,学生自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论.理解三角形的外角的两条性质以及三角形的内角和与外角和.活动意图说明:引导学生建立模型,鼓励学生大胆探索,经历三角形内角和外角关系的探究过程,在探究中发展合情推理的能力.使学生学会探索数学问题的归纳法和实验法等研究方法.积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1 如图, 是的边上的高,, . 求的度数. 解 在中, (直角三角形的两个锐角互余), (等式性质) . 又(已知), (等量代换) . 在中, (三角形的内角和等于 180°), (等式性质) . 又 (已求), (已知), (等量代换) . 例2如图,是的 边上一点,,,. 求:(1)的度数; (2)的度数. 【分析】(1)先由三角形外角的性质得出,再由,即可得出的度数;(2)直接根据三角形的内角和定理得出的度数. 【解】(1) 是的外角(已知), (三角形的一个外角等于与它不相邻的两个内角的和). 又(已知), (等量代换). (2)(三角形的内角和等于), . . (等式的性质).学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 活动意图说明: 让学生在一定的数学活动中去体验、感受数学,掌握三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,三角形的外角和等于360°.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 8.1 三角形 8.1.2 三角形的内角和与外角和 1.三角形的内角和定理及推理证明. 2.三角形的外角及外角和. 3.探索证明“三角形的一个外角等于和它不相邻的两个内角的和”的方法. 4.探索三角形的外角和. 例1 例2
课堂练习 【知识技能类作业】 必做题: 1.将一块含有角的直角三角板和一把直尺按如图所示的方式摆放,若,则∠2的度数是( ) A. B. C. D. 2.小明观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知,,则的度数是( ) A. B. C. D. 3.如图是某款婴儿手推车的平面示意图,若,,,则的度数为( ) A. B. C. D. 选做题: 4.已知一张三角形纸片(如图甲),其中.将纸片沿过点的直线折叠,使点落到边上的点处,折痕为(如图乙).再将纸片沿过点的直线折叠,使点恰好与点重合,折痕为(如图丙).原三角形纸片中,的大小为( ) A. B. C. D. 5.把一块直尺与一块三角板如图放置,若,则的度数为 . 6.在中,,射线平分,P为边上一点,,垂足为O,则的度数为 . 【综合拓展类作业】 7.如图,AD为△ABC的中线,BE为△ABD的中线. (1)∠ABE=15°,∠BAD=40°,求∠BED的度数; (2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少 答案: 1.B 2.D 3.D 4.C 5.【答案】 【知识点】三角形的外角性质;同位角的概念 6.【答案】或 【知识点】三角形内角和定理;三角形的外角性质 7.【答案】(1)解:∵∠BED是△ABE的角∴∠BED=∠ABE+∠BAD又∴∠ABE=15°∠BAD=40° ∴∠BED=55° (2)△BDE的面积=40×=10,所以E到BC边的距离 =10÷÷5=8.
作业设计 【知识技能类作业】 必做题: 1.已知三角形一个内角的度数为70°,则x+y的值为( ) A.180 B.110 C.100 D.70 2.在△ABC中,∠A=10°,∠B=60°,则△ABC的形状是( ) A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形 3.物理课上,小明研究一个小木块沿斜坡向下滑动时的运动状态,如图,∠C=90°,∠B=13°,小木块(△DEF)在AB上,且EF∥AC,则∠DFE的度数为( ) A.13° B.77° C.87° D.63° 选做题: 4.如果将一副三角板按如图所示的方式叠放,那么∠α的度数是( ) A.75° B.100° C.105° D.135° 5.如图,AD平分∠BAC,∠B=35°,∠ADC=82°,则∠C= °. 6.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=36°,∠E=24°,则∠BAC= °. 【综合拓展类作业】 7.实验证明平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 阅读以上材料并解决下列问题. (1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,求∠2及∠3的度数. 解:易知∠1=∠4,∠5=∠6,∴∠7=180°-∠1-∠4= ,∵m∥n, ∴∠2+∠7=180°,∴∠2=180°-∠7= ,∴∠5=∠6= ,根据三角形内角和为180°,知∠3=180°-∠4-∠5= . 在(1)中,①若∠1=55°,则∠3= ;②若∠1=40°,则 ∠3= . (3)由(1)(2),请你猜想:当两平面镜a、b的夹角∠3为多少度时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行 请你写出推理过程. 答案: 1.B 由题图可知,x+y=180-70=110.故选B. 2.A ∵∠A=10°,∠B=60°,∴∠C=180°-∠A-∠B=180°-10°-60°=110°,∴△ABC是钝角三角形.故选A. 3.B ∵∠C=90°,∠B=13°,∴∠A=180°-∠C-∠B=77°,∵EF∥AC,∴∠DFE=∠A=77°.故选B. 4.C 解法一:如图,由题意可得∠1=30°,则∠2=45°-∠1=45°-30°=15°,∴∠α=90°+∠2=105°.故选C. 解法二:如上图,∵∠1=30°,∴∠3=180°-(30°+45°)=105°, ∴∠α=∠3=105°.故选C. 5.51 解析 ∵∠ADC是△ABD的外角,∴∠BAD=∠ADC-∠B=82°-35°=47°,∵AD平分∠BAC,∴∠BAC=2∠BAD=94°, ∴∠C=180°-∠B-∠BAC=51°. 6.84 解析 ∵∠B=36°,∠E=24°,∴∠ECD=∠B+∠E=36°+24°=60°. ∵CE为∠ACD的平分线,∴∠ACD=2∠ECD=120°.又∵∠ACD=∠B+∠BAC,∴∠BAC=∠ACD-∠B=120°-36°=84°. 7.解析 (1)80°;100°;40°;90°. (2)①∵∠1=55°,∴∠4=∠1=55°,∴∠7=180°-(∠1+∠4)=180°-110°=70°.∵m∥n,∴∠2=180°-∠7=180°-70°=110°.∵∠5=∠6,∴∠5=(180°-∠2)=×70°=35°.又∵∠3+∠4+∠5=180°, ∴∠3=180°-∠4-∠5=180°-55°-35°=90°. ②∵∠1=40°,∴∠4=∠1=40°,∴∠7=180°-(∠1+∠4)=180°-80°=100°.∵m∥n,∴∠2=180°-∠7=180°-100°=80°.∵∠5=∠6,∴∠5=(180°-∠2)=×100°=50°.又∵∠3+∠4+∠5=180°, ∴∠3=180°-∠4-∠5=180°-40°-50°=90°. (3)根据平面镜反射光线的规律可知,∠1=∠4,∠5=∠6,∵m∥n,∴∠2+∠7=180°,∵∠1+∠4+∠7=180°,∠2+∠5+∠6=180°,∴2(∠5+∠4)+(∠2+∠7)=360°,∴∠5+∠4=×(360°-180°)=90°.∵∠3+∠4+∠5=180°,∴∠3=180°-(∠4+∠5)=180°-90°=90°, ∴当∠3=90°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.
教学反思 三角形的内角和外角的性质反映了三角形的内角和外角是互相联系与制约的,我们可以用它来求三角形的内角或外角.解题时,有时还需添加辅助线,有时结合代数,用方程来解比较方便.
21世纪教育网(www.21cnjy.com)
