华师大版七下(2024版)8.1.2三角形的内角和与外角和 课件
文档属性
| 名称 | 华师大版七下(2024版)8.1.2三角形的内角和与外角和 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
第八章 三角形
8.1.2三角形的内角和与外角和
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
02
教学目标
让学生在操作活动中,探索并了解三角形的内角和、三角形的外角的两条性质以及三角形的外角和.
01
利用平行线性质来证明三角形的内角和、三角形的外角的第一个性质以及三角形的外角和.
02
会利用“三角形的一个外角等于与它不相邻的两个内角的和”进行有关计算.
03
03
新知导入
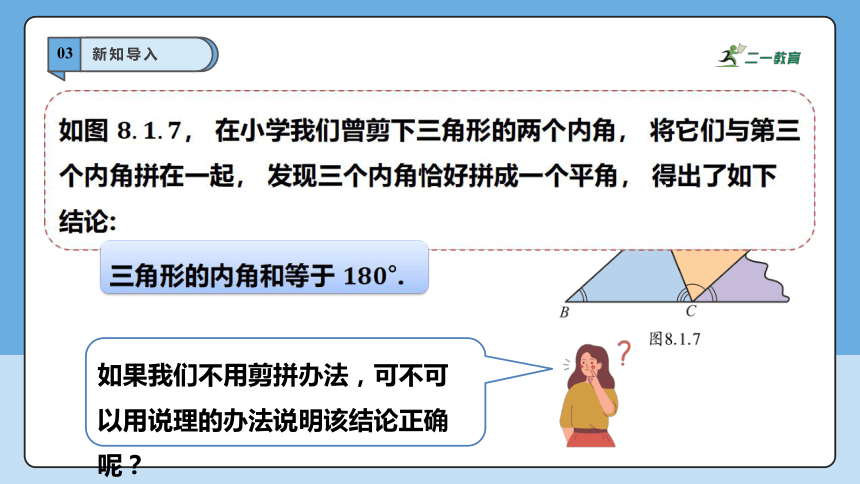
如图 , 在小学我们曾剪下三角形的两个内角, 将它们与第三个内角拼在一起, 发现三个内角恰好拼成一个平角, 得出了如下结论:
三角形的内角和等于 .
如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?
03
新知探究
探究1
三角形的内角和定理的推理证明
如图,已知 ,分别用,,表示的三个内角,证明.
【解】如图,延长到,以点为顶点,在的上侧作,则(同位角相等,两直线平行).
,
(两直线平行,内错角相等).
又,
(等量代换).
03
新知探究
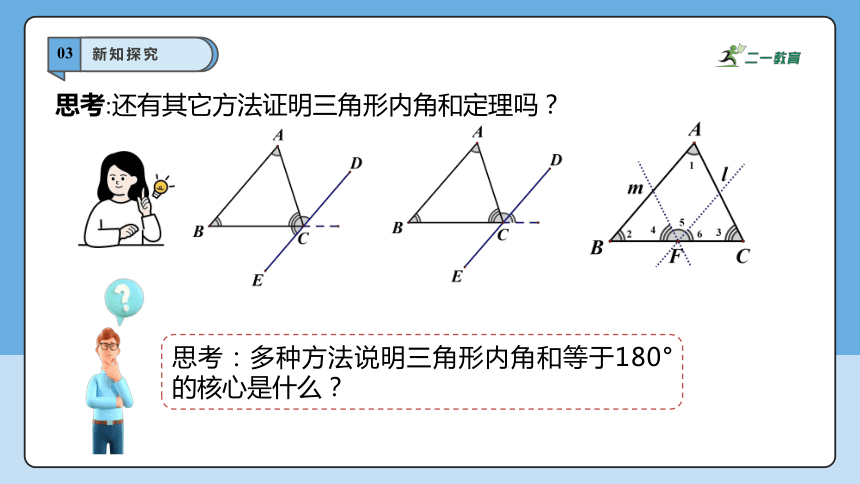
思考:还有其它方法证明三角形内角和定理吗?
思考:多种方法说明三角形内角和等于180°的核心是什么?
03
新知探究
1.在这里,为了需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
2.为了说明三角形三个内角的和为180°,常将三个角转化为一个平角,这种转化思想是数学中常用的方法.
总结
像上证明三角形内角和的方法都是通过作一边的平行线,利用平行线的性质,将三个角转化为一个角。
注意
03
新知探究
如图 8.1.10, 在直角三角形ABC中, ∠C = 90°,∠A与∠B有什么关系
由于三角形的内角和等于,得
.
,
由此可以推出
.
即与互余.
直角三角形的两个锐角互余。
概括
03
新知探究
直角三角形可以用符号 “Rt△”表示,直角三角 形ABC可以写成Rt△ABC .
几何语言:
∵ △ABC 是直角三角形,∠C=90°,
∴∠A+∠B=90°.
03
新知探究
我们已经知道,直角三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗
有两个角互余的三角形是直角三角形.
你能说明其理由吗?
如图:由于三角形的内角和等于,得
.
,
.
即△ABC是直角三角形.
03
新知探究
探究2
三角形的外角及外角和
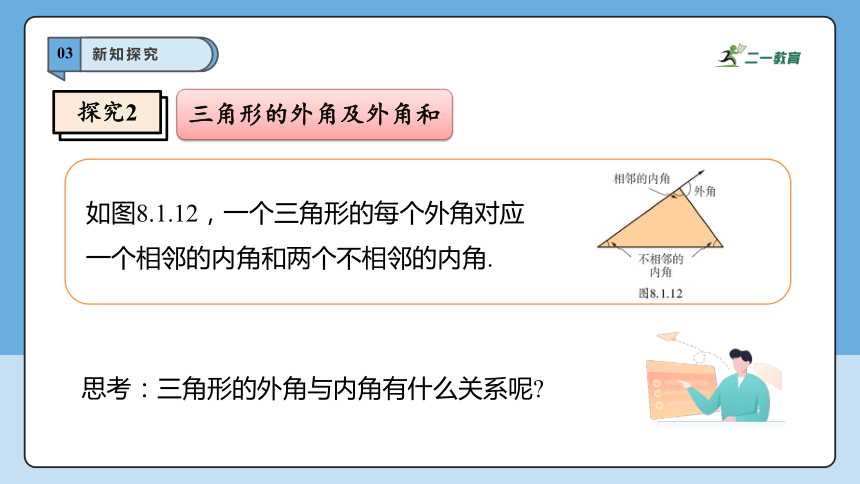
如图8.1.12,一个三角形的每个外角对应一个相邻的内角和两个不相邻的内角.
思考:三角形的外角与内角有什么关系呢
03
新知探究
探究2
三角形的外角及外角和
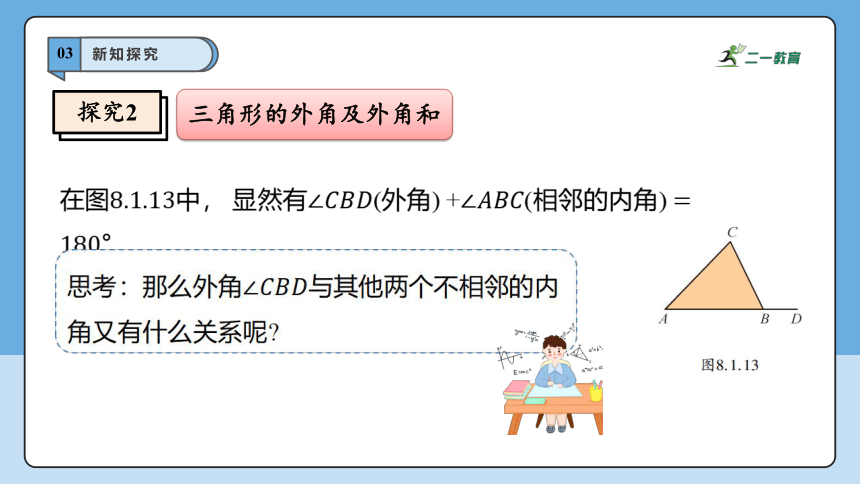
在图中, 显然有(外角) +(相邻的内角) .
思考:那么外角与其他两个不相邻的内角又有什么关系呢
03
新知探究
探究2
三角形的外角及外角和
依据三角形的内角和等于,
我们有.
由上面两个式子,可以推出
,
.
因而可以得到你与你的同伴所发现的结论:
.
03
新知探究
三角形的外角有两条性质:
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于任何一个与它不相邻的内角.
概括
如图,D是△ABC的边BC上一点,则有:
03
新知探究
你能用“三角形的内角和等于180°”来说明三角形的一个外角等于和它不相邻的两个内角的和吗
【解】如图,因为三角形的内角和等于,
所以°.
因为
,
所以.
03
新知探究
你能否从前面的操作中,得到说明三角形外角性质的另一种方法?
【解】如图,过点B作BE//AC,
所以.
因为
所以.
03
新知探究
探究3
探索三角形的外角和
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图所示,就是的外角和.
03
新知探究
在图中,
_______,_______,
_______.
三式相加可以得到
_______+_______+_______=_______①
而,②
将①与②相比较,你能得出什么结论
可以得到∠1 +∠2 +∠3 = 360°.
由此可知:三角形的外角和等于360°.
概括
02
新知探究
02
新知探究
你能由下图说明这一结论吗?
解:因为,
所以,(两直线平行,同位角相等).
因为,
所以(等量代换).
04
例题讲解
例1
解 在中,
(直角三角形的两个锐角互余),
(等式性质) .
又(已知),
(等量代换) .
在中,
(三角形的内角和等于 180°),
(等式性质) .
又 (已求), (已知),
(等量代换) .
如图, 是的边上的高,, 求的度数.
04
例题讲解
例2
分析
(1)先由三角形外角的性质得出∠ADC=∠B+∠BAD,再由∠ADC=80°,∠B=∠BAD即可得出∠B的度数;
(2)直接根据三角形的内角和定理得出∠C的度数.
如图,是的 边上一点,,,.
求:(1)的度数;
(2)的度数.
03
新知讲解
【解】(1) 是的外角(已知),
(三角形的一个外角等于与它不相邻的两个内角的和).
又(已知),
(等量代换).
(2)(三角形的内角和等于),
.
.
(等式的性质).
1.将一块含有角的直角三角板和一把直尺按如图所示的方式摆放,若,则∠2的度数是( )
A. B. C. D.
04
课堂练习
【知识技能类作业】必做题:
B
D
2.小明观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知,,则的度数是( )
A.29° B.30° C.31° D.33°
04
课堂练习
【知识技能类作业】必做题:
3.如图是某款婴儿手推车的平面示意图,若AB∥CD,∠1=130°,∠3=25°,则∠2的度数为( )
A.50° B.65° C.85° D.75°
D
04
课堂练习
【知识技能类作业】选做题:
4.已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,使点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠A的大小为( )
A.30° B.32° C.36° D.40°
C
04
课堂练习
【知识技能类作业】选做题:
5.把一块直尺与一块三角板如图放置,若,则的度数为 .
6.在中,,射线平分,P为边上一点,,垂足为O,则的度数为 .
44°
10°或170°
04
课堂练习
【综合拓展类作业】
7.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少
(1)解:∵∠BED是△ABE的角,
∴∠BED=∠ABE+∠BAD
又∵∠ABE=15°,∠BAD=40°
∴∠BED=55°
(2)△BDE的面积=40×=10,
所以E到BC边的距离 =10÷÷5=8.
05
课堂小结
三角形的内角和与外角和
三角形的内角和为180°.
三角形内角和定理
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于任何一个与它不相邻的内角.
三角形外角性质
直角三角形的两个锐角互余.
三角形的外角和等于360°.
三角形外角和
1.已知三角形一个内角的度数为70°,则x+y的值为( )
A.180 B.110 C.100 D.70
06
作业布置
【知识技能类作业】必做题:
B
A
2.在△ABC中,∠A=10°,∠B=60°,则△ABC的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
3.物理课上,小明研究一个小木块沿斜坡向下滑动时的运动状态,如图,∠C=90°,∠B=13°,小木块(△DEF)在AB上,且EF∥AC,则∠DFE的度数为( )
A.13° B.77° C.87° D.63°
B
4.如果将一副三角板按如图所示的方式叠放,那么∠α的度数是( )
A.75° B.100° C.105° D.135°
06
作业布置
【知识技能类作业】选做题:
C
5.如图,AD平分∠BAC,∠B=35°,∠ADC=82°,则∠C= °.
6.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=36°,∠E=24°,则∠BAC= °.
51
84
06
作业布置
【知识技能类作业】选做题:
7.实验证明平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
阅读以上材料并解决下列问题.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,求∠2及∠3的度数.
解:易知∠1=∠4,∠5=∠6,
∴∠7=180°-∠1-∠4= ,
∵m∥n,
∴∠2+∠7=180°,
∴∠2=180°-∠7= ,
∴∠5=∠6= ,
根据三角形内角和为180°,
知∠3=180°-∠4-∠5= .
06
作业布置
【知识技能类作业】选做题:
7.实验证明平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
阅读以上材料并解决下列问题.
(2)在(1)中,①若∠1=55°,则∠3= ;
②若∠1=40°,则∠3= .
(3)由(1)(2),请你猜想:当两平面镜a、b的夹角∠3为多少度时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行 请你写出推理过程.
(3)根据平面镜反射光线的规律知,,
,
,
当时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第八章 三角形
8.1.2三角形的内角和与外角和
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
02
教学目标
让学生在操作活动中,探索并了解三角形的内角和、三角形的外角的两条性质以及三角形的外角和.
01
利用平行线性质来证明三角形的内角和、三角形的外角的第一个性质以及三角形的外角和.
02
会利用“三角形的一个外角等于与它不相邻的两个内角的和”进行有关计算.
03
03
新知导入
如图 , 在小学我们曾剪下三角形的两个内角, 将它们与第三个内角拼在一起, 发现三个内角恰好拼成一个平角, 得出了如下结论:
三角形的内角和等于 .
如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?
03
新知探究
探究1
三角形的内角和定理的推理证明
如图,已知 ,分别用,,表示的三个内角,证明.
【解】如图,延长到,以点为顶点,在的上侧作,则(同位角相等,两直线平行).
,
(两直线平行,内错角相等).
又,
(等量代换).
03
新知探究
思考:还有其它方法证明三角形内角和定理吗?
思考:多种方法说明三角形内角和等于180°的核心是什么?
03
新知探究
1.在这里,为了需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
2.为了说明三角形三个内角的和为180°,常将三个角转化为一个平角,这种转化思想是数学中常用的方法.
总结
像上证明三角形内角和的方法都是通过作一边的平行线,利用平行线的性质,将三个角转化为一个角。
注意
03
新知探究
如图 8.1.10, 在直角三角形ABC中, ∠C = 90°,∠A与∠B有什么关系
由于三角形的内角和等于,得
.
,
由此可以推出
.
即与互余.
直角三角形的两个锐角互余。
概括
03
新知探究
直角三角形可以用符号 “Rt△”表示,直角三角 形ABC可以写成Rt△ABC .
几何语言:
∵ △ABC 是直角三角形,∠C=90°,
∴∠A+∠B=90°.
03
新知探究
我们已经知道,直角三角形的两个锐角互余.反过来,有两个角互余的三角形是直角三角形吗
有两个角互余的三角形是直角三角形.
你能说明其理由吗?
如图:由于三角形的内角和等于,得
.
,
.
即△ABC是直角三角形.
03
新知探究
探究2
三角形的外角及外角和
如图8.1.12,一个三角形的每个外角对应一个相邻的内角和两个不相邻的内角.
思考:三角形的外角与内角有什么关系呢
03
新知探究
探究2
三角形的外角及外角和
在图中, 显然有(外角) +(相邻的内角) .
思考:那么外角与其他两个不相邻的内角又有什么关系呢
03
新知探究
探究2
三角形的外角及外角和
依据三角形的内角和等于,
我们有.
由上面两个式子,可以推出
,
.
因而可以得到你与你的同伴所发现的结论:
.
03
新知探究
三角形的外角有两条性质:
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于任何一个与它不相邻的内角.
概括
如图,D是△ABC的边BC上一点,则有:
03
新知探究
你能用“三角形的内角和等于180°”来说明三角形的一个外角等于和它不相邻的两个内角的和吗
【解】如图,因为三角形的内角和等于,
所以°.
因为
,
所以.
03
新知探究
你能否从前面的操作中,得到说明三角形外角性质的另一种方法?
【解】如图,过点B作BE//AC,
所以.
因为
所以.
03
新知探究
探究3
探索三角形的外角和
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图所示,就是的外角和.
03
新知探究
在图中,
_______,_______,
_______.
三式相加可以得到
_______+_______+_______=_______①
而,②
将①与②相比较,你能得出什么结论
可以得到∠1 +∠2 +∠3 = 360°.
由此可知:三角形的外角和等于360°.
概括
02
新知探究
02
新知探究
你能由下图说明这一结论吗?
解:因为,
所以,(两直线平行,同位角相等).
因为,
所以(等量代换).
04
例题讲解
例1
解 在中,
(直角三角形的两个锐角互余),
(等式性质) .
又(已知),
(等量代换) .
在中,
(三角形的内角和等于 180°),
(等式性质) .
又 (已求), (已知),
(等量代换) .
如图, 是的边上的高,, 求的度数.
04
例题讲解
例2
分析
(1)先由三角形外角的性质得出∠ADC=∠B+∠BAD,再由∠ADC=80°,∠B=∠BAD即可得出∠B的度数;
(2)直接根据三角形的内角和定理得出∠C的度数.
如图,是的 边上一点,,,.
求:(1)的度数;
(2)的度数.
03
新知讲解
【解】(1) 是的外角(已知),
(三角形的一个外角等于与它不相邻的两个内角的和).
又(已知),
(等量代换).
(2)(三角形的内角和等于),
.
.
(等式的性质).
1.将一块含有角的直角三角板和一把直尺按如图所示的方式摆放,若,则∠2的度数是( )
A. B. C. D.
04
课堂练习
【知识技能类作业】必做题:
B
D
2.小明观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知,,则的度数是( )
A.29° B.30° C.31° D.33°
04
课堂练习
【知识技能类作业】必做题:
3.如图是某款婴儿手推车的平面示意图,若AB∥CD,∠1=130°,∠3=25°,则∠2的度数为( )
A.50° B.65° C.85° D.75°
D
04
课堂练习
【知识技能类作业】选做题:
4.已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,使点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠A的大小为( )
A.30° B.32° C.36° D.40°
C
04
课堂练习
【知识技能类作业】选做题:
5.把一块直尺与一块三角板如图放置,若,则的度数为 .
6.在中,,射线平分,P为边上一点,,垂足为O,则的度数为 .
44°
10°或170°
04
课堂练习
【综合拓展类作业】
7.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少
(1)解:∵∠BED是△ABE的角,
∴∠BED=∠ABE+∠BAD
又∵∠ABE=15°,∠BAD=40°
∴∠BED=55°
(2)△BDE的面积=40×=10,
所以E到BC边的距离 =10÷÷5=8.
05
课堂小结
三角形的内角和与外角和
三角形的内角和为180°.
三角形内角和定理
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于任何一个与它不相邻的内角.
三角形外角性质
直角三角形的两个锐角互余.
三角形的外角和等于360°.
三角形外角和
1.已知三角形一个内角的度数为70°,则x+y的值为( )
A.180 B.110 C.100 D.70
06
作业布置
【知识技能类作业】必做题:
B
A
2.在△ABC中,∠A=10°,∠B=60°,则△ABC的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
3.物理课上,小明研究一个小木块沿斜坡向下滑动时的运动状态,如图,∠C=90°,∠B=13°,小木块(△DEF)在AB上,且EF∥AC,则∠DFE的度数为( )
A.13° B.77° C.87° D.63°
B
4.如果将一副三角板按如图所示的方式叠放,那么∠α的度数是( )
A.75° B.100° C.105° D.135°
06
作业布置
【知识技能类作业】选做题:
C
5.如图,AD平分∠BAC,∠B=35°,∠ADC=82°,则∠C= °.
6.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=36°,∠E=24°,则∠BAC= °.
51
84
06
作业布置
【知识技能类作业】选做题:
7.实验证明平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
阅读以上材料并解决下列问题.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,求∠2及∠3的度数.
解:易知∠1=∠4,∠5=∠6,
∴∠7=180°-∠1-∠4= ,
∵m∥n,
∴∠2+∠7=180°,
∴∠2=180°-∠7= ,
∴∠5=∠6= ,
根据三角形内角和为180°,
知∠3=180°-∠4-∠5= .
06
作业布置
【知识技能类作业】选做题:
7.实验证明平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
阅读以上材料并解决下列问题.
(2)在(1)中,①若∠1=55°,则∠3= ;
②若∠1=40°,则∠3= .
(3)由(1)(2),请你猜想:当两平面镜a、b的夹角∠3为多少度时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行 请你写出推理过程.
(3)根据平面镜反射光线的规律知,,
,
,
当时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
