【课堂无忧】北师大版六下4.2《正比例》(课件)
文档属性
| 名称 | 【课堂无忧】北师大版六下4.2《正比例》(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 00:00:00 | ||
图片预览








文档简介
(共36张PPT)
第二课时
正比例
(北师大)六年级
下
01
学习目标
内容总览
02
新知导入
03
探究新知
04
课堂练习
05
课堂总结
06
分层作业
核心素养目标
结合“正方形的周长与边长,正方形的面积与边长,路程、时间与速度”等情境,经历正比例意义的建构过程,能从变化中看到“不变”,认识正比例。
01
02
能根据正比例的意义,判断两个相关联的量是不是成正比例,能举出生活中成正比例的实例,感受正比例在生活中的广泛应用。
03
经历比较、分析、归纳等数学活动,提高分析比较、归纳概括能力,初步体会函数思想。
新知导入
李啊姨驾车去中国最美的乡村——婺源游玩。
新知导入
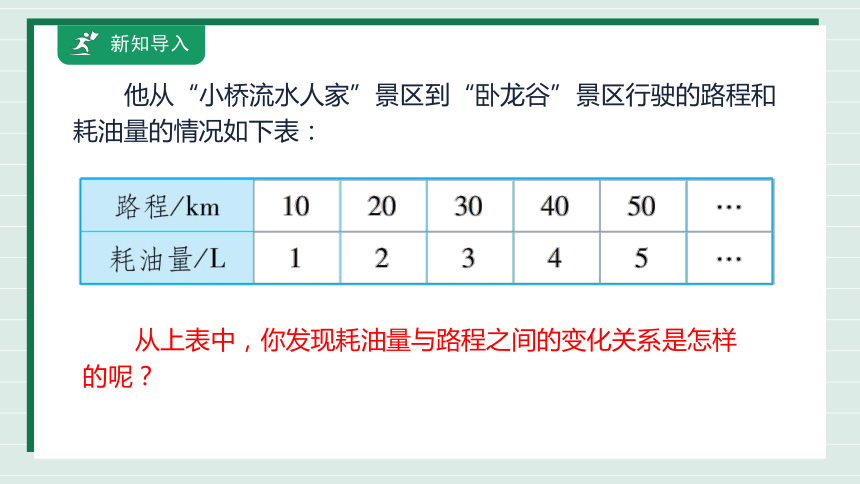
他从“小桥流水人家”景区到“卧龙谷”景区行驶的路程和耗油量的情况如下表:
从上表中,你发现耗油量与路程之间的变化关系是怎样的呢?
学习任务一
认识正比例
探究新知
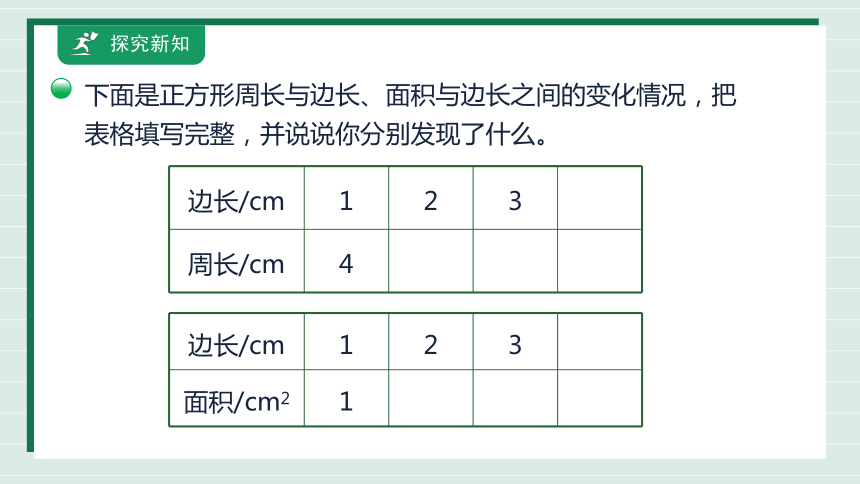
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
探究新知
小组合作要求:
1.先把表格填写完整。
2.观察表一边长和周长发生变化了吗?它们是怎样变化的?
3.观察表二边长和面积发生变化了吗?它们是怎样变化的?
4.周长与边长、面积与边长之间的变化规律相同吗?
探究新知
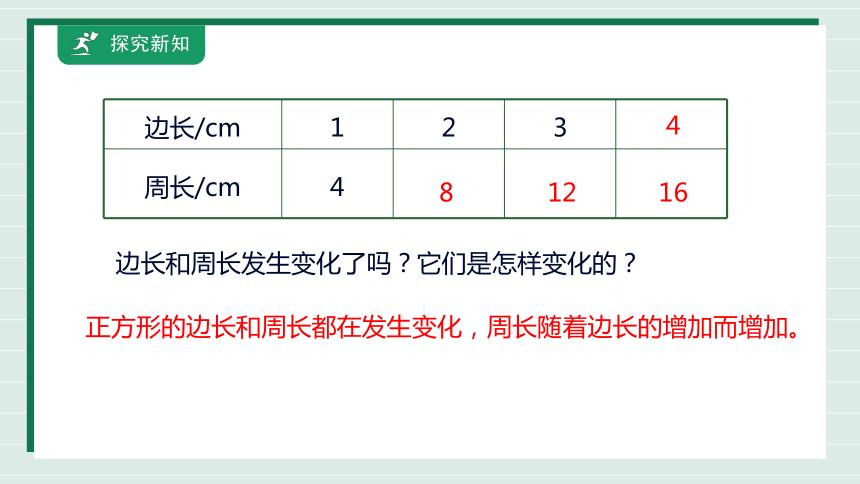
边长/cm 1 2 3
周长/cm 4
8
12
16
4
正方形的边长和周长都在发生变化,周长随着边长的增加而增加。
边长和周长发生变化了吗?它们是怎样变化的?
探究新知
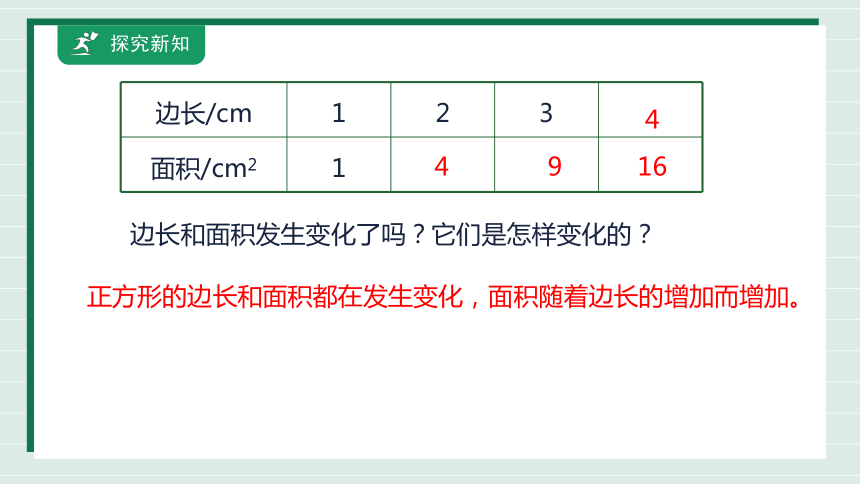
边长/cm 1 2 3
面积/cm2 1
4
9
16
4
正方形的边长和面积都在发生变化,面积随着边长的增加而增加。
边长和面积发生变化了吗?它们是怎样变化的?
探究新知
说说你发现了什么?
边长/cm 1 2 3
周长/cm 4
8
12
16
4
边长/cm 1 2 3
面积/cm2 1
4
9
16
4
探究新知
周长与边长、面积与边长之间的变化规律相同吗?
周长与边长的比值不变。
面积与边长
的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
探究新知
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整。
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
8
720
当时间变化时,路程也随着变化,路程随着时间的增加而增加。
当时间发生变化时,路程怎样变化?变化有什么规律?
你从表中发现了什么?
路程与时间的比值是一定的。
探究新知
时间是1,路程是90;
时间是2,路程是180;
时间是3,路程是270;
时间是4,路程是360;
路程随着时间的变化而变化。
时间扩大,路程随着
扩大。
时间缩小,路程随着
缩小。
探究新知
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
路程
时间
=速度
(一定)
时间和路程是两种相关联的量:
探究新知
周长与边长的比值不变。
面积与边长
的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
正方形的周长和边长成正比例。
正方形的面积和边长不成正比例。
探究新知
怎样判断两个量能否组成正比例。
两个量是不是相关联的量。
两个量的变化方向是否一致。
两个量的比值是否一定。
学习任务二
判断两个量是否成正比例的方法
探究新知
圆的面积与半径成正比例吗?你是怎么想的?与同伴交流。
圆的面积随着半径的变化而变化。
圆的面积 3.14 12.56 28.26
半径 1 2 3
圆的面积与半径的比值不相等。
圆的面积与半径不成正比例。
S=πr 2
3.14
1
=3.14
12.562
=6.28
28.26
3
=9.42
探究新知
乐乐和爸爸的年龄变化情况如下,把表填写完整。
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
34
乐乐的年龄与爸爸年龄的比值不是一个确定的值,
他们的年龄成正比例吗?为什么?
35
36
37
所以,他们的年龄不成正比例。
32 16 33 33 34 17
6 3 7 7 8 4
=
=
=
两个变量是否成正比例,关键是它们的比值是否一定。
探究新知
分别举一个成正比例和一个不成正比例的例子,与同伴交流。
圆的半径与周长成正比例。
圆的周长
半径
一本书看的页数与未看的页数不成正比例。看的页数+未看的页数=书的总页数(一定),它们的和一定,但比值不一定。
= 2π(一定)
课堂练习
1.学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
(1)说一说竿影的长与竹竿的高的变化关系。
(2)写出竿影的长与竹竿的高的比,你有什么发现?
(3)竹竿的高与竿影的长是不是成正比例?说明理由。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
课堂练习
(1)说一说竿影的长与竹竿的高的变化关系。
竿影的长随着竹竿的高的变化而变化。
(2)写出竿影的长与竹竿的高的比,你有什么发现?
0.4∶1 0.8∶2 1.2∶3
1.6∶4 2.4∶6 3.2∶8
竿影的长与竹竿的高的比值都是0.4。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
课堂练习
(3)竹竿的高与竿影的长是不是成正比例?说明理由。
因为
竿影的长
竹竿的高
=0.4(一定)
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
竹竿的高与竿影的长成正比例。
课堂练习
2.根据下表中底是6cm的平行四边形的面积与高相对应的
数据,判断他们是不是成正比例,并说明理由。
平行四边形的面积/cm2 6 12 18 24 30
平行四边形的高/cm 1 2 3 4 5
平行四边形的面积
平行四边形的高
=6(一定)
平行四边形的面积与高成正比例。
课堂练习
3.判断下面各题中的两个量是否成正比例,并说明理由。
(1)每袋大米的质量一定,大米的总质量和袋数。
(2)一个人的身高和年龄。
(3)宽不变,长方形的周长与长。
(1)大米的总质量和袋数成正比例。
大米的总质量∶袋数=每袋大米的质量(一定)
(2)一个人的身高和年龄不成正比例。
因这一个人的身高长到一定高度就不长了,但年龄还在变化。
课堂练习
3.判断下面各题中的两个量是否成正比例,并说明理由。
(1)每袋大米的质量一定,大米的总质量和袋数。
(2)一个人的身高和年龄。
(3)宽不变,长方形的周长与长。
(3)长方形的周长与长不成正比例。
长方形的长 1 2 3
长方形的周长 4 6 8
它们的比值不相等。
假设宽是1不变
课堂练习
买邮票的数量/枚 应付金额/元
1 0.8
2 1.6
3
4
5
6
7
8
4.把表填完整,你从中发现了什么?应付金额与所买邮票的
数量成正比例吗?
2.4
3.2
4
4.8
5.6
6.4
=0.8(一定)
应付金额
买邮票的数量
课堂总结
今天你有什么收获?
分层作业
【知识技能类作业】
1.赵阿姨购买苹果的质量和应付的钱数如下表。
(1)赵阿姨应付的钱数随着购买苹果的质量的增加而( )。
增加
分层作业
(2)计算比值:14:2=( ), 21:3=( ),
28:4=( ), 35:5=( ), 42:6=( )。
发现:应付的钱数和购买苹果的质量的比值( )一定,所以它们成( )比例。
7
7
7
7
7
1.赵阿姨购买苹果的质量和应付的钱数如下表。
也就是单价
正
分层作业
2.判断下面各题中的两个量是否成正比例,并说明理由。
(1)车轮的周长一定,所行路程与车轮转的圈数。
答:成正比例。 =车轮的周长(一定),
它们的比值一定,所以所行路程和车轮转的圈数成正比例。
所行路程
车轮转的圈数
分层作业
(2)两个数的和一定,加数和另一个加数。
答:不成正比例。加数+另一个加数=和(一定),
它们的和一定,但比值不一定,所以加数和另一个加数不成正比例。
分层作业
【综合实践类作业】
3.下面是一根木料锯的次数、锯成的段数与所需的时间之间的关系分析表。
(1)表中的哪两个量成正比例 说明理由。
表中锯木料所需的时间与锯的次数成正比例。
因为 =2,比值一定,所以锯木料所需的时间与锯的次数成正比例。
2
1
4
2
6
3
8
4
10
5
=
=
=
=
分层作业
3.下面是一根木料锯的次数、锯成的段数与所需的时间之间的关系分析表。
(2)若将这根木料锯成8段,需要多少分
将这根木料锯成8段,需要锯7次。
解:设需要x分。
x=14
答:需要 14 分。
10
5
=
x
7
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
第二课时
正比例
(北师大)六年级
下
01
学习目标
内容总览
02
新知导入
03
探究新知
04
课堂练习
05
课堂总结
06
分层作业
核心素养目标
结合“正方形的周长与边长,正方形的面积与边长,路程、时间与速度”等情境,经历正比例意义的建构过程,能从变化中看到“不变”,认识正比例。
01
02
能根据正比例的意义,判断两个相关联的量是不是成正比例,能举出生活中成正比例的实例,感受正比例在生活中的广泛应用。
03
经历比较、分析、归纳等数学活动,提高分析比较、归纳概括能力,初步体会函数思想。
新知导入
李啊姨驾车去中国最美的乡村——婺源游玩。
新知导入
他从“小桥流水人家”景区到“卧龙谷”景区行驶的路程和耗油量的情况如下表:
从上表中,你发现耗油量与路程之间的变化关系是怎样的呢?
学习任务一
认识正比例
探究新知
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
探究新知
小组合作要求:
1.先把表格填写完整。
2.观察表一边长和周长发生变化了吗?它们是怎样变化的?
3.观察表二边长和面积发生变化了吗?它们是怎样变化的?
4.周长与边长、面积与边长之间的变化规律相同吗?
探究新知
边长/cm 1 2 3
周长/cm 4
8
12
16
4
正方形的边长和周长都在发生变化,周长随着边长的增加而增加。
边长和周长发生变化了吗?它们是怎样变化的?
探究新知
边长/cm 1 2 3
面积/cm2 1
4
9
16
4
正方形的边长和面积都在发生变化,面积随着边长的增加而增加。
边长和面积发生变化了吗?它们是怎样变化的?
探究新知
说说你发现了什么?
边长/cm 1 2 3
周长/cm 4
8
12
16
4
边长/cm 1 2 3
面积/cm2 1
4
9
16
4
探究新知
周长与边长、面积与边长之间的变化规律相同吗?
周长与边长的比值不变。
面积与边长
的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
探究新知
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整。
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
8
720
当时间变化时,路程也随着变化,路程随着时间的增加而增加。
当时间发生变化时,路程怎样变化?变化有什么规律?
你从表中发现了什么?
路程与时间的比值是一定的。
探究新知
时间是1,路程是90;
时间是2,路程是180;
时间是3,路程是270;
时间是4,路程是360;
路程随着时间的变化而变化。
时间扩大,路程随着
扩大。
时间缩小,路程随着
缩小。
探究新知
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
路程
时间
=速度
(一定)
时间和路程是两种相关联的量:
探究新知
周长与边长的比值不变。
面积与边长
的比值不相等。
周长随着边长的变化而变化。
面积随着边长的变化而变化。
正方形的周长和边长成正比例。
正方形的面积和边长不成正比例。
探究新知
怎样判断两个量能否组成正比例。
两个量是不是相关联的量。
两个量的变化方向是否一致。
两个量的比值是否一定。
学习任务二
判断两个量是否成正比例的方法
探究新知
圆的面积与半径成正比例吗?你是怎么想的?与同伴交流。
圆的面积随着半径的变化而变化。
圆的面积 3.14 12.56 28.26
半径 1 2 3
圆的面积与半径的比值不相等。
圆的面积与半径不成正比例。
S=πr 2
3.14
1
=3.14
12.562
=6.28
28.26
3
=9.42
探究新知
乐乐和爸爸的年龄变化情况如下,把表填写完整。
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
34
乐乐的年龄与爸爸年龄的比值不是一个确定的值,
他们的年龄成正比例吗?为什么?
35
36
37
所以,他们的年龄不成正比例。
32 16 33 33 34 17
6 3 7 7 8 4
=
=
=
两个变量是否成正比例,关键是它们的比值是否一定。
探究新知
分别举一个成正比例和一个不成正比例的例子,与同伴交流。
圆的半径与周长成正比例。
圆的周长
半径
一本书看的页数与未看的页数不成正比例。看的页数+未看的页数=书的总页数(一定),它们的和一定,但比值不一定。
= 2π(一定)
课堂练习
1.学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
(1)说一说竿影的长与竹竿的高的变化关系。
(2)写出竿影的长与竹竿的高的比,你有什么发现?
(3)竹竿的高与竿影的长是不是成正比例?说明理由。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
课堂练习
(1)说一说竿影的长与竹竿的高的变化关系。
竿影的长随着竹竿的高的变化而变化。
(2)写出竿影的长与竹竿的高的比,你有什么发现?
0.4∶1 0.8∶2 1.2∶3
1.6∶4 2.4∶6 3.2∶8
竿影的长与竹竿的高的比值都是0.4。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
课堂练习
(3)竹竿的高与竿影的长是不是成正比例?说明理由。
因为
竿影的长
竹竿的高
=0.4(一定)
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
竹竿的高与竿影的长成正比例。
课堂练习
2.根据下表中底是6cm的平行四边形的面积与高相对应的
数据,判断他们是不是成正比例,并说明理由。
平行四边形的面积/cm2 6 12 18 24 30
平行四边形的高/cm 1 2 3 4 5
平行四边形的面积
平行四边形的高
=6(一定)
平行四边形的面积与高成正比例。
课堂练习
3.判断下面各题中的两个量是否成正比例,并说明理由。
(1)每袋大米的质量一定,大米的总质量和袋数。
(2)一个人的身高和年龄。
(3)宽不变,长方形的周长与长。
(1)大米的总质量和袋数成正比例。
大米的总质量∶袋数=每袋大米的质量(一定)
(2)一个人的身高和年龄不成正比例。
因这一个人的身高长到一定高度就不长了,但年龄还在变化。
课堂练习
3.判断下面各题中的两个量是否成正比例,并说明理由。
(1)每袋大米的质量一定,大米的总质量和袋数。
(2)一个人的身高和年龄。
(3)宽不变,长方形的周长与长。
(3)长方形的周长与长不成正比例。
长方形的长 1 2 3
长方形的周长 4 6 8
它们的比值不相等。
假设宽是1不变
课堂练习
买邮票的数量/枚 应付金额/元
1 0.8
2 1.6
3
4
5
6
7
8
4.把表填完整,你从中发现了什么?应付金额与所买邮票的
数量成正比例吗?
2.4
3.2
4
4.8
5.6
6.4
=0.8(一定)
应付金额
买邮票的数量
课堂总结
今天你有什么收获?
分层作业
【知识技能类作业】
1.赵阿姨购买苹果的质量和应付的钱数如下表。
(1)赵阿姨应付的钱数随着购买苹果的质量的增加而( )。
增加
分层作业
(2)计算比值:14:2=( ), 21:3=( ),
28:4=( ), 35:5=( ), 42:6=( )。
发现:应付的钱数和购买苹果的质量的比值( )一定,所以它们成( )比例。
7
7
7
7
7
1.赵阿姨购买苹果的质量和应付的钱数如下表。
也就是单价
正
分层作业
2.判断下面各题中的两个量是否成正比例,并说明理由。
(1)车轮的周长一定,所行路程与车轮转的圈数。
答:成正比例。 =车轮的周长(一定),
它们的比值一定,所以所行路程和车轮转的圈数成正比例。
所行路程
车轮转的圈数
分层作业
(2)两个数的和一定,加数和另一个加数。
答:不成正比例。加数+另一个加数=和(一定),
它们的和一定,但比值不一定,所以加数和另一个加数不成正比例。
分层作业
【综合实践类作业】
3.下面是一根木料锯的次数、锯成的段数与所需的时间之间的关系分析表。
(1)表中的哪两个量成正比例 说明理由。
表中锯木料所需的时间与锯的次数成正比例。
因为 =2,比值一定,所以锯木料所需的时间与锯的次数成正比例。
2
1
4
2
6
3
8
4
10
5
=
=
=
=
分层作业
3.下面是一根木料锯的次数、锯成的段数与所需的时间之间的关系分析表。
(2)若将这根木料锯成8段,需要多少分
将这根木料锯成8段,需要锯7次。
解:设需要x分。
x=14
答:需要 14 分。
10
5
=
x
7
https://www.21cnjy.com/help/help_extract.php
让备课更有效
www.21cnjy.com
Thanks!
