第17章 勾股定理 能力提升测试题(含解析)
文档属性
| 名称 | 第17章 勾股定理 能力提升测试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 16:25:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第17章 勾股定理 能力提升测试题
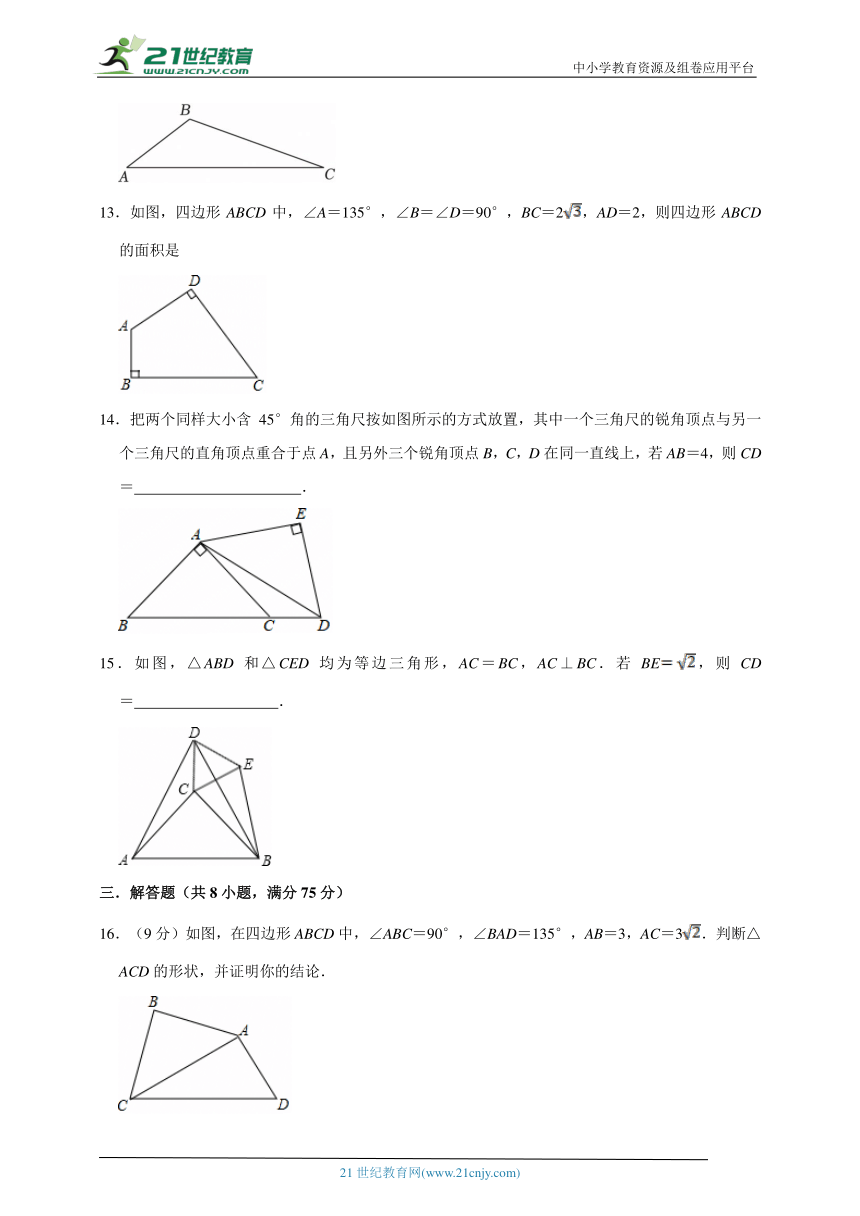
考试范围:第17章 勾股定理;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.若a,b为直角三角形的两直角边,c为斜边,下列选项中不能用来证明勾股定理的是( )
A. B. C. D.
2.下列各命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等 D.如果两个角都是45°,那么这两个角相等
3.以下列各组数为边长,能构成直角三角形的是( )
A.9,12,15 B.32,42,52 C.6,7,8 D.4,5,6
4.在Rt△ABC中,已知其两边长分别为a,b,且满足(a﹣3)2+|b﹣4|=0,则该直角三角形的斜边长为( )
A.5 B. C.5或 D.5或4
5.如图,正方形OABC的边长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A.1 B.1.5 C. D.
6.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是( )
A.4 B.3 C.2 D.
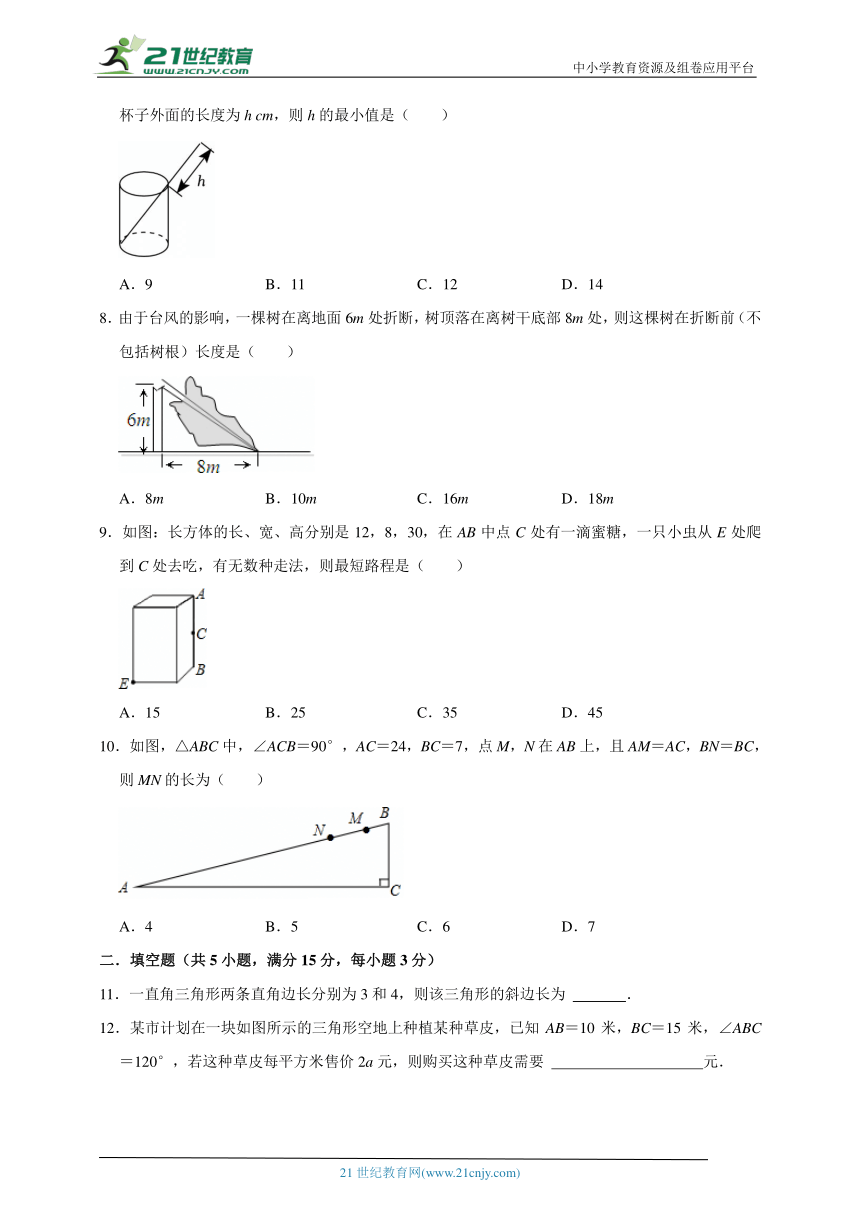
7.如图,圆柱形杯子底面直径为7cm,高为24cm.将一根长36cm的木棒斜放在杯中,设木棒露在杯子外面的长度为h cm,则h的最小值是( )
A.9 B.11 C.12 D.14
8.由于台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树在折断前(不包括树根)长度是( )
A.8m B.10m C.16m D.18m
9.如图:长方体的长、宽、高分别是12,8,30,在AB中点C处有一滴蜜糖,一只小虫从E处爬到C处去吃,有无数种走法,则最短路程是( )
A.15 B.25 C.35 D.45
10.如图,△ABC中,∠ACB=90°,AC=24,BC=7,点M,N在AB上,且AM=AC,BN=BC,则MN的长为( )
A.4 B.5 C.6 D.7
二.填空题(共5小题,满分15分,每小题3分)
11.一直角三角形两条直角边长分别为3和4,则该三角形的斜边长为 .
12.某市计划在一块如图所示的三角形空地上种植某种草皮,已知AB=10米,BC=15米,∠ABC=120°,若这种草皮每平方米售价2a元,则购买这种草皮需要 元.
13.如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2,AD=2,则四边形ABCD的面积是
14.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上,若AB=4,则CD= .
15.如图,△ABD和△CED均为等边三角形,AC=BC,AC⊥BC.若BE,则CD= .
三.解答题(共8小题,满分75分)
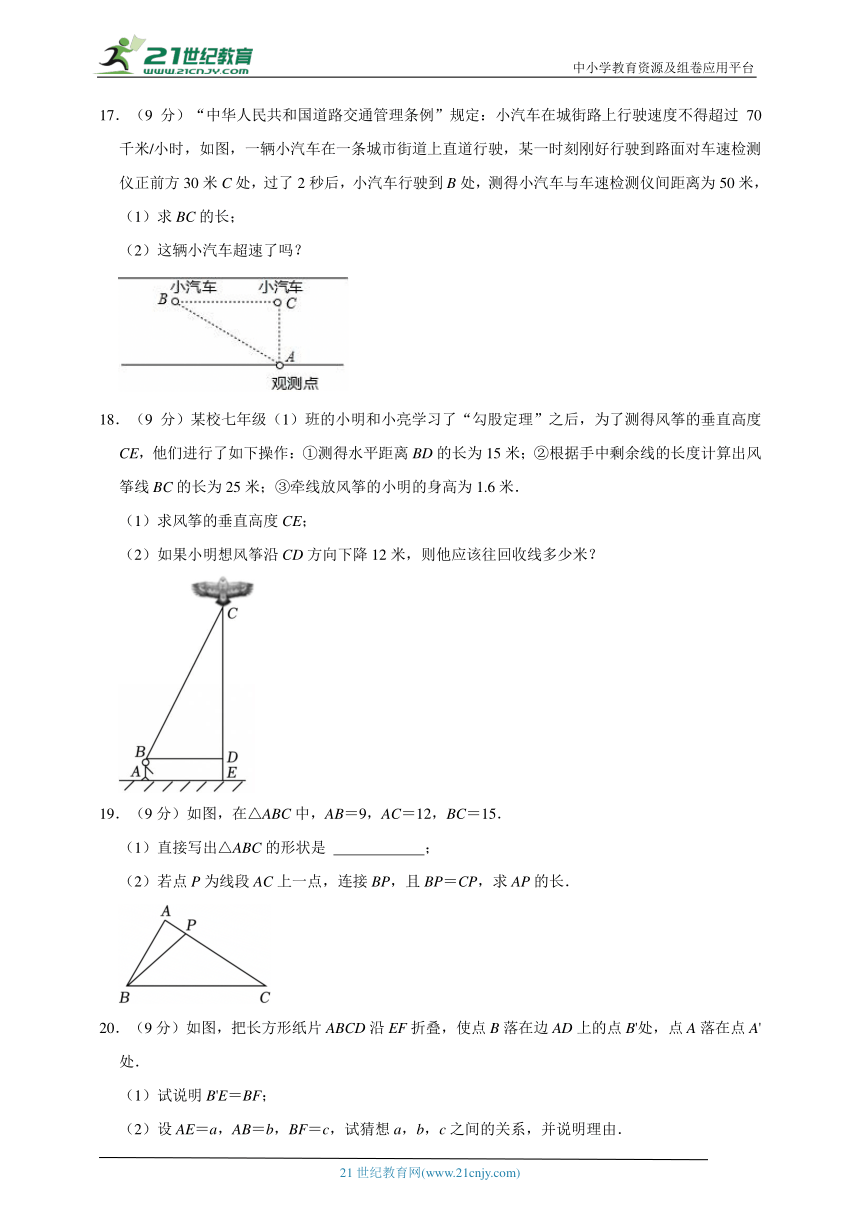
16.(9分)如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=3,AC=3.判断△ACD的形状,并证明你的结论.
17.(9分)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30米C处,过了2秒后,小汽车行驶到B处,测得小汽车与车速检测仪间距离为50米,
(1)求BC的长;
(2)这辆小汽车超速了吗?
18.(9分)某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?
19.(9分)如图,在△ABC中,AB=9,AC=12,BC=15.
(1)直接写出△ABC的形状是 ;
(2)若点P为线段AC上一点,连接BP,且BP=CP,求AP的长.
20.(9分)如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的关系,并说明理由.
21.(9分)如图,直角三角形ACB,直角顶点C在直线l上,分别过点A、B作直线l的垂线,垂足分别为点D和点E.
(1)求证:∠DAC=∠BCE;
(2)如果AC=BC.
①求证:CD=BE;
②若设△ADC的三边分别为a、b、c,试用此图证明勾股定理.
22.(10分)如图,铁路MN和铁路PO在P点处交汇,点A处是第九十四中学,AP=160米,点A到铁路MN的距离为80米,假使火车行驶时,周围100米以内会受到噪音影响,火车在铁路MN上沿PN方向行驶时.
(1)学校是否会受到影响?请说明理由;
(2)如果受到影响,已知火车的速度是50米/秒那么学校受到影响的时间是多久?
23.(11分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.
(1)当t=2时,CD= ,AD= ;
(2)求当t为何值时,△CBD是直角三角形,说明理由;
(3)求当t为何值时,△CBD是以BD或CD为底的等腰三角形?并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:选项A不能用来证明勾股定理,符合题意;
选项B,正方形的面积=4ab+(b﹣a)2=+2ab+a2+b2﹣2ab=a2+b2=c2,不符合题意;
选项C,正方形的面积=(a+b)2=4ab+c2,
化简得,a2+b2=c2,不符合题意;
选项D,梯形的面积(a+b)(a+b)=2abc2,
化简得,a2+b2=c2,不符合题意;
选:A.
2.解:A、逆命题是三个角对应相等的两个三角形全等,错误;
B、绝对值相等的两个数相等,错误;
C、同位角相等,两条直线平行,正确;
D、相等的两个角都是45°,错误.
选:C.
3.解:A、92+122=225=152,A能构成直角三角形,符合题意;
B、(32)2+(42)2=337≠(52)2,B不能构成直角三角形,不符合题意;
C、62+72=85≠82,C不能构成直角三角形,不符合题意;
D、42+52=41≠62,D不能构成直角三角形,不符合题意;
选:A.
4.解:由(a﹣3)2+|b﹣4|=0得,a=3,b=4;
①若a,b是直角边,则斜边长为5,
②∵b>a,
∴若b是斜边,则斜边长为4.
综上,该直角三角形的斜边长为5或4.
选:D.
5.解:∵正方形OABC的边长为1,OA在数轴上,
∴OA=AB=1,∠OAB=90°,
在直角三角形AOB中,由勾股定理得:,
∴这个点表示的实数是,
选:D.
6.解:作DE⊥AB于E,
∵AD是∠BAC的平分线,∠ACB=90°,DE⊥AB,
∴DE=DC=2,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
由勾股定理得BE2,
设AC=AE=x,
由勾股定理得x2+62=(x+2)2,
解得x=2.
选:C.
7.解:∵将一根长为36cm的筷子,置于底面直径为7cm,高为24cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短是等于杯子的高时,h=36﹣24=12(cm),
最长时等于杯子斜边长度是:,
此时h=36﹣25=11,
∴h的取值范围是:11≤h≤12,
即h的最小值是11.
选:B.
8.解:由题意得BC=8m,AC=6m,
在直角三角形ABC中,根据勾股定理得:AB10米.
所以大树的高度是10+6=16米.
选:C.
9.解:如图展开,连接EC,则线段EC的长就是小虫爬的最短路线,
在Rt△EBC中,BE=12+8=20,BCAB=15,由勾股定理得:EC25.
选:B.
10.解:∵在△ABC中,∠ACB=90°,AC=24,CB=7,
∴根据勾股定理得:AB25,
又AM=AC,BN=BC,
则MN=AM+BN﹣AB=AC+BC﹣AB=24+7﹣25=6.
选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.解:这个直角三角形的斜边长5,
答案为:5.
12.解:如图,作BA边的高CD,设与AB的延长线交于点D,
∵∠ABC=120°,
∴∠DBC=60°,
∴∠BCD=30°,
∴BDBC米,
∴CD米,
∵AB=10米,
∴S△ABCAB CD10(平方米),
∵每平方米售价2a元,
∴购买这种草皮至少为 2a=75a(元),
答案为:75a.
13.解:延长BA、CD交于点E,
∵∠BAD=135°,
∴∠EAD=45°,
∴ED=AD=2,EB=BC=2,
∴四边形ABCD的面积222×2=4,
答案为:4.
14.解:如图,过点A作AF⊥BC于F,
在Rt△ABC中,∠B=45°,
∴BCAB=4,FC=BF=AFAB=2,
∵两个同样大小的含45°角的三角尺,
∴AD=BC=4,
在Rt△ADF中,根据勾股定理得,DF2,
∴CD=DF﹣FC=22,
答案为:22.
15.解:延长DC交AB于F.
∵CA=CB,DA=DB
∴CD均在线段AB的垂直平分线上,即DF⊥AB,且∠CDB=30°
∴BD为等边△CDE中∠CDE的角平分线,∠CDB=∠EDB
在△CDB和△EDB中,
∴△CDB≌△EDB(SAS),
∴BE=BC.
∵AC⊥BC,
∴∠ACB=90°,
∵AC=BC,
∴AB2,且DF,
且CF=BF=1,
∴CD的长为DF﹣CF1.
答案为1.
三.解答题(共8小题,满分75分)
16.证明:Rt△ABC中,∵∠ABC=90°,AB=3,AC=3,
∴BC2=(3)2﹣32=9,
∴BC=3,
∴BC=AB,
∴∠BCA=∠BAC=45°,
又∵∠BAD=135°,
∴∠CAD=135﹣45°=90°,
∴△ACD是直角三角形.
17.解:(1)在直角△ABC中,已知AC=30米,AB=50米,
且AB为斜边,则BC40米.
答:小汽车在2秒内行驶的距离BC为40米;
(2)小汽车在2秒内行驶了40米,所以平均速度为20米/秒,
20米/秒=72千米/时,
因为72>70,
所以这辆小汽车超速了.
答:这辆小汽车的平均速度大于70千米/时,这辆小汽车超速了.
18.解:(1)在Rt△CDB中,BC=25米,BD=15米,
由勾股定理得:CD20(米),
∴CE=CD+DE=20+1.6=21.6(米),
答:风筝的垂直高度CE为21.6 米;
(2)如图,设下降到M,连接BM,
由题意可知,CM=12米,
∴DM=CD﹣CM=20﹣12=8(米),
∴BM17(米),
∴BC﹣BM=25﹣17=8(米),
答:他应该往回收线8米.
19.解(1)在△ABC中,AB=9,AC=12,BC=15,
∴AB2+AC2=92+122=225,BC2=152=225,
∴AB2+AC2=BC2,
∴△ABC是直角三角形.
答案为:直角三角形;
(2)依题意有:92+AP2=(12﹣AP)2,
解得AP=2.625.
AP的长是2.625.
20.(1)证明:由折叠的性质得:B'F=BF,∠B'FE=∠BFE,
在长方形纸片ABCD中,AD∥BC,
∴∠B'EF=∠BFE,
∴∠B'FE=∠B'EF,
∴B'F=B'E,
∴B'E=BF.
(2)解:a,b,c之间的关系是a2+b2=c2.理由如下:
由(1)知B'E=BF=c,
由折叠的性质得:∠A'=∠A=90°,A'E=AE=a,A'B'=AB=b.
在△A'B'E中,∵∠A'=90°,
∴A'E2+A'B'2=B'E2,
∴a2+b2=c2.
21.证明:(1)∵∠ACB=90°,AD⊥DE于点D,
∴∠DAC+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠DAC=∠BCE;
(2)①∵AD⊥DE于点D,BE⊥DE于点E,
∴∠ADC=∠CEB=90°,
由(1)知:∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CD=BE;
②由图可知:
S梯形ADEB=S△ADC+S△ACB+S△CEB,
∴,
化简,得:a2+b2=c2.
22.解:(1)会受到影响,理由如下:
过点A作AE⊥MN于点E,
∵点A到铁路MN的距离为80米,
∴AE=80m,
∵周围100米以内会受到噪音影响,80<100,
∴学校会受到影响;
(2)以点A为圆心,100米为半径画圆,交直线MN于BC两点,连接AB,AC,则AB=AC=100m,
在Rt△ABE中,
∵AB=100m,AE=80m,
∴,
∴BC=2BE=120m,
∴.
答:学校受到影响的时间是2.4秒.
23.解:(1)t=2时,CD=2×1=2,
∵∠ABC=90°,AB=8,BC=6,
∴AC10,
AD=AC﹣CD=10﹣2=8;
答案为:2;8.
(2)①∠CDB=90°时,S△ABCAC BDAB BC,
即10 BD8×6,
解得BD=4.8,
∴CD3.6,
t=3.6÷1=3.6秒;
②∠CBD=90°时,点D和点A重合,
t=10÷1=10秒,
综上所述,t=3.6或10秒;
答案为:(1)2,8;(2)3.6或10秒;
(3)①CD=BC时,CD=6,t=6÷1=6;
②BD=BC时,如图,过点B作BF⊥AC于F,
则CF=3.6,
CD=2CF=3.6×2=7.2,
∴t=7.2÷1=7.2,
综上所述,t=6秒或7.2秒时,△CBD是以BD或CD为底的等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第17章 勾股定理 能力提升测试题
考试范围:第17章 勾股定理;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.若a,b为直角三角形的两直角边,c为斜边,下列选项中不能用来证明勾股定理的是( )
A. B. C. D.
2.下列各命题的逆命题成立的是( )
A.全等三角形的对应角相等 B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等 D.如果两个角都是45°,那么这两个角相等
3.以下列各组数为边长,能构成直角三角形的是( )
A.9,12,15 B.32,42,52 C.6,7,8 D.4,5,6
4.在Rt△ABC中,已知其两边长分别为a,b,且满足(a﹣3)2+|b﹣4|=0,则该直角三角形的斜边长为( )
A.5 B. C.5或 D.5或4
5.如图,正方形OABC的边长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A.1 B.1.5 C. D.
6.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是( )
A.4 B.3 C.2 D.
7.如图,圆柱形杯子底面直径为7cm,高为24cm.将一根长36cm的木棒斜放在杯中,设木棒露在杯子外面的长度为h cm,则h的最小值是( )
A.9 B.11 C.12 D.14
8.由于台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树在折断前(不包括树根)长度是( )
A.8m B.10m C.16m D.18m
9.如图:长方体的长、宽、高分别是12,8,30,在AB中点C处有一滴蜜糖,一只小虫从E处爬到C处去吃,有无数种走法,则最短路程是( )
A.15 B.25 C.35 D.45
10.如图,△ABC中,∠ACB=90°,AC=24,BC=7,点M,N在AB上,且AM=AC,BN=BC,则MN的长为( )
A.4 B.5 C.6 D.7
二.填空题(共5小题,满分15分,每小题3分)
11.一直角三角形两条直角边长分别为3和4,则该三角形的斜边长为 .
12.某市计划在一块如图所示的三角形空地上种植某种草皮,已知AB=10米,BC=15米,∠ABC=120°,若这种草皮每平方米售价2a元,则购买这种草皮需要 元.
13.如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2,AD=2,则四边形ABCD的面积是
14.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上,若AB=4,则CD= .
15.如图,△ABD和△CED均为等边三角形,AC=BC,AC⊥BC.若BE,则CD= .
三.解答题(共8小题,满分75分)
16.(9分)如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=3,AC=3.判断△ACD的形状,并证明你的结论.
17.(9分)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30米C处,过了2秒后,小汽车行驶到B处,测得小汽车与车速检测仪间距离为50米,
(1)求BC的长;
(2)这辆小汽车超速了吗?
18.(9分)某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?
19.(9分)如图,在△ABC中,AB=9,AC=12,BC=15.
(1)直接写出△ABC的形状是 ;
(2)若点P为线段AC上一点,连接BP,且BP=CP,求AP的长.
20.(9分)如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的关系,并说明理由.
21.(9分)如图,直角三角形ACB,直角顶点C在直线l上,分别过点A、B作直线l的垂线,垂足分别为点D和点E.
(1)求证:∠DAC=∠BCE;
(2)如果AC=BC.
①求证:CD=BE;
②若设△ADC的三边分别为a、b、c,试用此图证明勾股定理.
22.(10分)如图,铁路MN和铁路PO在P点处交汇,点A处是第九十四中学,AP=160米,点A到铁路MN的距离为80米,假使火车行驶时,周围100米以内会受到噪音影响,火车在铁路MN上沿PN方向行驶时.
(1)学校是否会受到影响?请说明理由;
(2)如果受到影响,已知火车的速度是50米/秒那么学校受到影响的时间是多久?
23.(11分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.
(1)当t=2时,CD= ,AD= ;
(2)求当t为何值时,△CBD是直角三角形,说明理由;
(3)求当t为何值时,△CBD是以BD或CD为底的等腰三角形?并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:选项A不能用来证明勾股定理,符合题意;
选项B,正方形的面积=4ab+(b﹣a)2=+2ab+a2+b2﹣2ab=a2+b2=c2,不符合题意;
选项C,正方形的面积=(a+b)2=4ab+c2,
化简得,a2+b2=c2,不符合题意;
选项D,梯形的面积(a+b)(a+b)=2abc2,
化简得,a2+b2=c2,不符合题意;
选:A.
2.解:A、逆命题是三个角对应相等的两个三角形全等,错误;
B、绝对值相等的两个数相等,错误;
C、同位角相等,两条直线平行,正确;
D、相等的两个角都是45°,错误.
选:C.
3.解:A、92+122=225=152,A能构成直角三角形,符合题意;
B、(32)2+(42)2=337≠(52)2,B不能构成直角三角形,不符合题意;
C、62+72=85≠82,C不能构成直角三角形,不符合题意;
D、42+52=41≠62,D不能构成直角三角形,不符合题意;
选:A.
4.解:由(a﹣3)2+|b﹣4|=0得,a=3,b=4;
①若a,b是直角边,则斜边长为5,
②∵b>a,
∴若b是斜边,则斜边长为4.
综上,该直角三角形的斜边长为5或4.
选:D.
5.解:∵正方形OABC的边长为1,OA在数轴上,
∴OA=AB=1,∠OAB=90°,
在直角三角形AOB中,由勾股定理得:,
∴这个点表示的实数是,
选:D.
6.解:作DE⊥AB于E,
∵AD是∠BAC的平分线,∠ACB=90°,DE⊥AB,
∴DE=DC=2,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
由勾股定理得BE2,
设AC=AE=x,
由勾股定理得x2+62=(x+2)2,
解得x=2.
选:C.
7.解:∵将一根长为36cm的筷子,置于底面直径为7cm,高为24cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短是等于杯子的高时,h=36﹣24=12(cm),
最长时等于杯子斜边长度是:,
此时h=36﹣25=11,
∴h的取值范围是:11≤h≤12,
即h的最小值是11.
选:B.
8.解:由题意得BC=8m,AC=6m,
在直角三角形ABC中,根据勾股定理得:AB10米.
所以大树的高度是10+6=16米.
选:C.
9.解:如图展开,连接EC,则线段EC的长就是小虫爬的最短路线,
在Rt△EBC中,BE=12+8=20,BCAB=15,由勾股定理得:EC25.
选:B.
10.解:∵在△ABC中,∠ACB=90°,AC=24,CB=7,
∴根据勾股定理得:AB25,
又AM=AC,BN=BC,
则MN=AM+BN﹣AB=AC+BC﹣AB=24+7﹣25=6.
选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.解:这个直角三角形的斜边长5,
答案为:5.
12.解:如图,作BA边的高CD,设与AB的延长线交于点D,
∵∠ABC=120°,
∴∠DBC=60°,
∴∠BCD=30°,
∴BDBC米,
∴CD米,
∵AB=10米,
∴S△ABCAB CD10(平方米),
∵每平方米售价2a元,
∴购买这种草皮至少为 2a=75a(元),
答案为:75a.
13.解:延长BA、CD交于点E,
∵∠BAD=135°,
∴∠EAD=45°,
∴ED=AD=2,EB=BC=2,
∴四边形ABCD的面积222×2=4,
答案为:4.
14.解:如图,过点A作AF⊥BC于F,
在Rt△ABC中,∠B=45°,
∴BCAB=4,FC=BF=AFAB=2,
∵两个同样大小的含45°角的三角尺,
∴AD=BC=4,
在Rt△ADF中,根据勾股定理得,DF2,
∴CD=DF﹣FC=22,
答案为:22.
15.解:延长DC交AB于F.
∵CA=CB,DA=DB
∴CD均在线段AB的垂直平分线上,即DF⊥AB,且∠CDB=30°
∴BD为等边△CDE中∠CDE的角平分线,∠CDB=∠EDB
在△CDB和△EDB中,
∴△CDB≌△EDB(SAS),
∴BE=BC.
∵AC⊥BC,
∴∠ACB=90°,
∵AC=BC,
∴AB2,且DF,
且CF=BF=1,
∴CD的长为DF﹣CF1.
答案为1.
三.解答题(共8小题,满分75分)
16.证明:Rt△ABC中,∵∠ABC=90°,AB=3,AC=3,
∴BC2=(3)2﹣32=9,
∴BC=3,
∴BC=AB,
∴∠BCA=∠BAC=45°,
又∵∠BAD=135°,
∴∠CAD=135﹣45°=90°,
∴△ACD是直角三角形.
17.解:(1)在直角△ABC中,已知AC=30米,AB=50米,
且AB为斜边,则BC40米.
答:小汽车在2秒内行驶的距离BC为40米;
(2)小汽车在2秒内行驶了40米,所以平均速度为20米/秒,
20米/秒=72千米/时,
因为72>70,
所以这辆小汽车超速了.
答:这辆小汽车的平均速度大于70千米/时,这辆小汽车超速了.
18.解:(1)在Rt△CDB中,BC=25米,BD=15米,
由勾股定理得:CD20(米),
∴CE=CD+DE=20+1.6=21.6(米),
答:风筝的垂直高度CE为21.6 米;
(2)如图,设下降到M,连接BM,
由题意可知,CM=12米,
∴DM=CD﹣CM=20﹣12=8(米),
∴BM17(米),
∴BC﹣BM=25﹣17=8(米),
答:他应该往回收线8米.
19.解(1)在△ABC中,AB=9,AC=12,BC=15,
∴AB2+AC2=92+122=225,BC2=152=225,
∴AB2+AC2=BC2,
∴△ABC是直角三角形.
答案为:直角三角形;
(2)依题意有:92+AP2=(12﹣AP)2,
解得AP=2.625.
AP的长是2.625.
20.(1)证明:由折叠的性质得:B'F=BF,∠B'FE=∠BFE,
在长方形纸片ABCD中,AD∥BC,
∴∠B'EF=∠BFE,
∴∠B'FE=∠B'EF,
∴B'F=B'E,
∴B'E=BF.
(2)解:a,b,c之间的关系是a2+b2=c2.理由如下:
由(1)知B'E=BF=c,
由折叠的性质得:∠A'=∠A=90°,A'E=AE=a,A'B'=AB=b.
在△A'B'E中,∵∠A'=90°,
∴A'E2+A'B'2=B'E2,
∴a2+b2=c2.
21.证明:(1)∵∠ACB=90°,AD⊥DE于点D,
∴∠DAC+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠DAC=∠BCE;
(2)①∵AD⊥DE于点D,BE⊥DE于点E,
∴∠ADC=∠CEB=90°,
由(1)知:∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CD=BE;
②由图可知:
S梯形ADEB=S△ADC+S△ACB+S△CEB,
∴,
化简,得:a2+b2=c2.
22.解:(1)会受到影响,理由如下:
过点A作AE⊥MN于点E,
∵点A到铁路MN的距离为80米,
∴AE=80m,
∵周围100米以内会受到噪音影响,80<100,
∴学校会受到影响;
(2)以点A为圆心,100米为半径画圆,交直线MN于BC两点,连接AB,AC,则AB=AC=100m,
在Rt△ABE中,
∵AB=100m,AE=80m,
∴,
∴BC=2BE=120m,
∴.
答:学校受到影响的时间是2.4秒.
23.解:(1)t=2时,CD=2×1=2,
∵∠ABC=90°,AB=8,BC=6,
∴AC10,
AD=AC﹣CD=10﹣2=8;
答案为:2;8.
(2)①∠CDB=90°时,S△ABCAC BDAB BC,
即10 BD8×6,
解得BD=4.8,
∴CD3.6,
t=3.6÷1=3.6秒;
②∠CBD=90°时,点D和点A重合,
t=10÷1=10秒,
综上所述,t=3.6或10秒;
答案为:(1)2,8;(2)3.6或10秒;
(3)①CD=BC时,CD=6,t=6÷1=6;
②BD=BC时,如图,过点B作BF⊥AC于F,
则CF=3.6,
CD=2CF=3.6×2=7.2,
∴t=7.2÷1=7.2,
综上所述,t=6秒或7.2秒时,△CBD是以BD或CD为底的等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
