8.34 概 率 2025年数学中考一轮专题复习课件(共51张PPT)
文档属性
| 名称 | 8.34 概 率 2025年数学中考一轮专题复习课件(共51张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 14:01:02 | ||
图片预览











文档简介
(共51张PPT)
2025年数学中考复习
8.34 概 率
基础知识
项目八 统计与概率
考点要求
壹
1.能通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定随机事件发生的所有可能结果,了解随机事件的概率;
2.知道通过大量重复试验,可以用频率估计概率.
核心知识点
贰
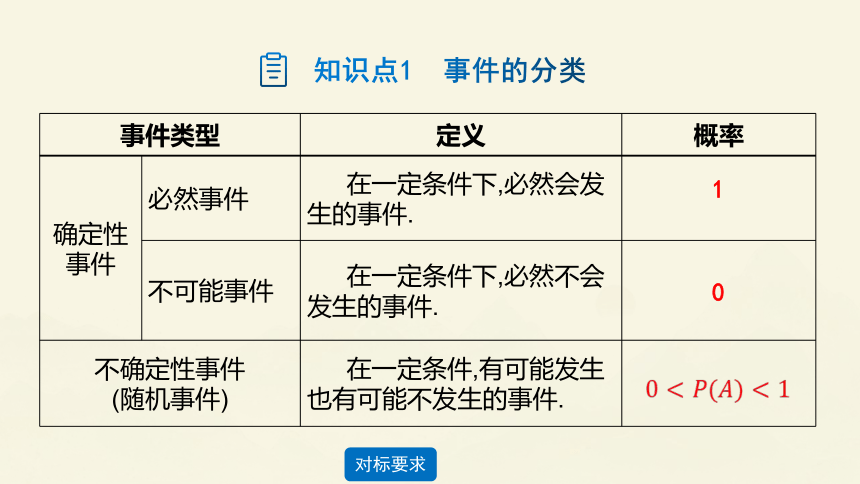
知识点1 事件的分类
事件类型 定义 概率
确定性事件 必然事件 在一定条件下,必然会发生的事件.
不可能事件 在一定条件下,必然不会发生的事件.
不确定性事件 (随机事件) 在一定条件,有可能发生也有可能不发生的事件.
1
0
知识点2 概率及计算
1. 概率定义:一般地,对于一个随机事件,我们把刻画其发生
的数值,称为随机事件发生的概率,记为.
2.概率的计算方法
可能性大小
知识点3 概率的应用
分析事件发生的可能性
概率在日常生活和科技方面有广泛应用,如彩票、中奖等.
判断游戏公平性
在条件相同的前提下,如果对于参加游戏的每一个人,获胜的概率均相同,则游戏公平,否则游戏不公平.
考点攻坚
叁
(2022·广西)下列事件是必然事件的是( )
A.三角形内角和是180°
B.端午节赛龙舟,红队获得冠军
C.掷一枚均匀骰子,点数是6的一面朝上
D.打开电视,正在播放神舟十四号载人飞船发射实况
考点1 事件的分类
例1
【解析】三角形内角和为180°为必然事件,故A选项符合题意;端午节赛龙舟,红队获得冠军是随机事件,故B选项不符合题意;掷一枚均匀骰子,点数是6的一面朝上是随机事件,故C选项不符合题意;打开电视,正在播放神舟十四号载人飞船发射实况是随机事件,故D选项不符合题意.故选A.
(2023·陕西)一个不透明的袋子中装有四个小球,这四个小球上各标有一个数字,分别是1,1,2,3.这些小球除标有的数字外都相同.
(1)从袋中机摸出一个小球,则摸出的这个小球上标有的数字是1的概率为 ;
(2)先从袋中随机摸出一个小球,记下小球上标有的数字后,放回,摇匀,再从袋中随机摸出一个小球,记下小球上标有的数字,请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积是偶数的概率.
考点2 概率及其计算
例2
考点3 概率的应用
例3
(2022·山东青岛)小冰和小雪参加航天知识竞赛时,均获得了一等奖,学校想请一位同学作为代表分享获奖心得.小冰和小雪都想分享,于是两人决定一起做游戏,谁获胜谁分享,游戏规则如下:甲口袋装有编号为1,2的两个球,乙口袋装有编号为1,2,3,4,5的五个球,两口袋中的球除编号外都相同.小冰先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球.若两球编号之和为奇数,则小冰获胜;若两球编号之和为偶数,则小雪获胜.请用列表或画树状图的方法,说明这个游戏对双方是否公平.
专项训练
肆
通关训练
1.(2022·湖北武汉)彩民李大叔购买1张彩票后中奖,这个事件是( )
A.必然事件 B.确定性事件
C.不可能事件 D.随机事件
D
2.(2023·广东)某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹任”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等.小明恰好选中“烹任”的概率为( )
C
3.(2024·广西)不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是( )
D
4.(2023·广西)某班开展“梦想未来、青春有我”主题班会,第一小组有2位男同学和3位女同学,现从中随机抽取1位同学分享个人感悟,则抽到男同学的概率是 .
5.(2023·湖南长沙)千门万户瞳瞳日,总把新桃换旧符.春节是中华民族的传统节日,古人常用写“桃符”的方式来祈福避祸,而现在人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.某商家在春节期间开展商品促销活动,顾客凡购物金额满100元,就可以从“福”字、春联、灯笼这三类礼品中免费领取一件.礼品领取规则:顾客每次从装有大小、形状、质地都相同的三张卡片(分别写有“福”字、春联、灯笼)的不透明袋子中,随机摸出一张卡片,然后领取一件与卡片上文字所对应的礼品,现有2名顾客都只领取了一件礼品,那么他们恰好领取同一类礼品的概率是( )
C
6.(2023·湖南湘潭)为落实“ 双减”政策要求,丰富学生课余生活,某校七年级根据学生需求,组建了四个社团供学生选择:(合唱社团)、(硬笔书法社团)、(街舞社团)、(面点社团).学生从中任意选择两个社团参加活动.
(1)小明对这4个社团都很感兴趣,如果他随机选择两个社团,请列举出所有的可能结果;
(2)小宇和小江在选择过程中,首先都选了社团(街舞社团),第二个社团他俩决定随机选择,请用列表法或树状图求他俩选到相同社团的概率.
6. 解:(1)所有的可能结果共有6种,分别为;
(2)画树状图如下:
共有9种等可能的结果,其中小宇和小江选到相同社团的结果有3种,他俩选到相同社团的概率为.
答案
提升训练
7.(2022·湖北武汉)班长邀请四位同学参加圆桌会议.如图所示,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则两位同学座位相邻的概率是( )
C
8.(2023·福建)为促进消费,助力经济发展,某商场决定“让利酬宾”,于五一期间举办了抽奖促销活动.活动规定:凡在商场消费一定金额的顾客,均可获得一次抽奖机会.抽奖方案如下:从装有大小质地完全相同的1个红球及编号为①②③的3个黄球的袋中,随机摸出1个球,若摸得红球,则中奖,可获得奖品;若摸得黄球,则不中奖.同时,还允许未中奖的顾客将其摸得的球放回袋中,并再往袋中加入1个红球或黄球(它们的大小质地与袋中的4个球完全相同),然后从中随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球,若摸得的两球的颜色相同,则该顾客可获得精美礼品一份.现已知某顾客获得抽奖机会.
(1)求该顾客首次摸球中奖的概率;
(2)假如该顾客首次摸球未中奖,为了有更大机会获得精美礼品,他应往袋中加入哪种颜色的球?说明你的理由.
答案
8. 解:(1)顾客首次摸球的所有可能结果为红,黄①,黄②,黄③,共4种等可能的结果,记“首次摸得红球”为事件,则事件发生的结果只有1种,
,顾客首次摸球中奖的概率为.
(2)他应往袋中加入黄球;理由如下:
记往袋中加入的球为“新”,摸得的两球所有可能的结果列表如下:
共有 20种等可能结果,
①若往袋中加入的是红球,两球颜色相同的结果共有8种,此时该顾客获得精美礼品的概率;②若往袋中加入的是黄球,两球颜色相同的结果共有12种,此时该顾客获得精美礼品的概率;,他应往袋中加入黄球.
课堂练习
伍
1.(2024·盘锦)下列事件是必然事件的是( )
A. 四边形内角和是360°
B. 校园排球比赛,九年一班获得冠军
C. 掷一枚硬币时,正面朝上
D. 打开电视,正在播放神舟十六号载人飞船发射实况
A
2.(2023·大理)在一个不透明的袋子中装有6个白球和14个红球,这些球除颜色外无其他差别,随机从袋子中摸出一个球,则摸到白球的概率为( )
C
A. B. C. D.
3.(2023·湖北襄阳)某校即将举行田 径运动会,“体育达人”小明从“跳高”“跳远” “100米”“400米”四个项目中,随机选择两项,则他选择“100米”与“400米”两个项目的概率是( )
C
A. B. C.
4.(2023·太原)某校在劳动课上,设置了植树、种花、除草三个劳动项目.九(1)班和九(2)班都通过抽签的方式从这三个项目中随机抽取一个项目,则这两个班级恰好都抽到种花的概率是( D )
A. B. C. D.
5.(2024·成都)不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是( )
D
A. C. D.
6.(2024·金华)如图所示,电路连接完好,且各元件工作正常.随机闭合开关,,中的两个,能让两个小灯泡同时发光的概率是( D )
A. B. C. D.
7.(2023·南京)某种绿豆在相同条件下发芽试验的结果如下表所示:
这种绿豆发芽的概率的估计值为 (精确到0.01)
0.93
每批粒数n 2 5 10 50 100 500 1000 1500 2000 3000
发芽的频数m 2 4 9 44 92 463 928 1396 1866 2794
发芽的频率 (精确到0.001) 1.000 0.800 0.900 0.880 0.920 0.926 0.928 0.931 0.933 0.931
8.(2023·杭州)在一个不透明的 口袋中装有红球和白球共12个,这些球除颜色外都相同,将口袋中的球搅匀后,从中随机摸出1个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸球200次,发现有50次摸 到红球,则口袋中红球约有 个.
3
9.(2024·肇庆)我国人工智能市场分为“决策类人工智能”“人工智能机器人”“语音及语义人工智能”“视觉人工智能”四大类型,将四个类型的图标分 别制成四张卡片(卡片背面完全相同),并把 四张卡片背面朝上洗匀,从中随机抽取一张,则抽到“视觉人工智能”的概率为(
10.(2024·广西模拟)我国空间站的主体结构包括核心舱、问天实验舱和梦天实验舱.假设甲、乙、丙三名航天员从核心舱进入实验舱的机会均等,现在要从这三名航天员中选2人进入梦天实验舱开展科学实验,则甲、乙两人同时被选中的概率为 .
11.已知五个红色研学基地,某地为了解中学生的意愿,随机抽取部分学生进行调查,并将统计数据整理后, 绘制了不完整的条形统计图和扇形统计图.
(1)请将条形统计图补充完整;
(2)在扇形统计图中,所在的扇形的圆心角的度数为 ;若该地区有1000名中学生参加研学活动,则愿意去基地的大约有 人;
(3)甲、乙两所学校计划从三个基地中任选一个基地开展研学活动,请利用树状图或表格求两校恰好选取同一个基地的概率.
11. 解:(1)本次抽取的学生有:(人),
其中选择的学生有:(人),
补全的条形统计图如图所示;
答案
答案
(2)在扇形统计图中,所在的扇形的圆心角的度数为:
,
该市有1000名中学生参加研学活动,愿意去A基地的大约有:
(人);
故答案为:14.4°;200;
答案
由上可得,一共有9种等可能性,其中两校恰好选取同一个基地的可能性有3种, ∴两校恰好选取同一个基地的概率为.
12.(2023·承德)“阅读新时代,书 香满宜昌”.在“全民阅读月”活动中,某校提 供了四类适合学生阅读的书籍:文学类,科幻类,漫画类,数理类.为了解学生阅读兴趣,学校随机抽取了部分学生进行调查(每位学生仅选一类).根据收集到的数据,整理后得到下列不完整的图表:
书籍类别 学生人数
A文学类 24
B科幻类 m
C漫画类 16
D数理类 8
(1)本次抽查的学生人数是 ,统计表中的 ;
(2)在扇形统计图中,“漫画类”对应的圆心角的度数是 ;
(3)若该校共有1200名学生,请你估计该校学生选择“数理类”书籍的学生人数;
(4)学校决定成立“文学”“科幻”“漫画” “数理”四个阅读社团.若小文、小明随机选取四个社团中的一个,请利用列表或画树状图的方法,求他们选择同一社团的概率.
答案
答:估计该校学生选择“数理类”书籍的学生人数约为120人;
12.(1)80,32
(2)72°;
(3)1200X=120(人).
答案
由上可得,一共有16种等可能性,其中他们选择同一社团的可能性有4种, ∴他们选择同一社团的概率为.
13.(2023·宁夏)劳动委员统计了某周全班同学的家庭劳动次数x(单位:次),按劳动次数分为4组:,,,,绘制成如图所示的频数分布直方图.从中任选一名同学,则该同学这周家庭劳动次数不足6次的概率是( )
A
A.0.6 B.0.5 C.0.4 D.0.32
14.(2022·靖江)如图所示,一张圆桌共有3个座位,甲、乙,丙3人随机坐到这3个座位上,则甲和乙相邻的概率为( D )
A. B. C. D.1
谢谢观看
2025年数学中考复习
8.34 概 率
基础知识
项目八 统计与概率
考点要求
壹
1.能通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定随机事件发生的所有可能结果,了解随机事件的概率;
2.知道通过大量重复试验,可以用频率估计概率.
核心知识点
贰
知识点1 事件的分类
事件类型 定义 概率
确定性事件 必然事件 在一定条件下,必然会发生的事件.
不可能事件 在一定条件下,必然不会发生的事件.
不确定性事件 (随机事件) 在一定条件,有可能发生也有可能不发生的事件.
1
0
知识点2 概率及计算
1. 概率定义:一般地,对于一个随机事件,我们把刻画其发生
的数值,称为随机事件发生的概率,记为.
2.概率的计算方法
可能性大小
知识点3 概率的应用
分析事件发生的可能性
概率在日常生活和科技方面有广泛应用,如彩票、中奖等.
判断游戏公平性
在条件相同的前提下,如果对于参加游戏的每一个人,获胜的概率均相同,则游戏公平,否则游戏不公平.
考点攻坚
叁
(2022·广西)下列事件是必然事件的是( )
A.三角形内角和是180°
B.端午节赛龙舟,红队获得冠军
C.掷一枚均匀骰子,点数是6的一面朝上
D.打开电视,正在播放神舟十四号载人飞船发射实况
考点1 事件的分类
例1
【解析】三角形内角和为180°为必然事件,故A选项符合题意;端午节赛龙舟,红队获得冠军是随机事件,故B选项不符合题意;掷一枚均匀骰子,点数是6的一面朝上是随机事件,故C选项不符合题意;打开电视,正在播放神舟十四号载人飞船发射实况是随机事件,故D选项不符合题意.故选A.
(2023·陕西)一个不透明的袋子中装有四个小球,这四个小球上各标有一个数字,分别是1,1,2,3.这些小球除标有的数字外都相同.
(1)从袋中机摸出一个小球,则摸出的这个小球上标有的数字是1的概率为 ;
(2)先从袋中随机摸出一个小球,记下小球上标有的数字后,放回,摇匀,再从袋中随机摸出一个小球,记下小球上标有的数字,请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积是偶数的概率.
考点2 概率及其计算
例2
考点3 概率的应用
例3
(2022·山东青岛)小冰和小雪参加航天知识竞赛时,均获得了一等奖,学校想请一位同学作为代表分享获奖心得.小冰和小雪都想分享,于是两人决定一起做游戏,谁获胜谁分享,游戏规则如下:甲口袋装有编号为1,2的两个球,乙口袋装有编号为1,2,3,4,5的五个球,两口袋中的球除编号外都相同.小冰先从甲口袋中随机摸出一个球,小雪再从乙口袋中随机摸出一个球.若两球编号之和为奇数,则小冰获胜;若两球编号之和为偶数,则小雪获胜.请用列表或画树状图的方法,说明这个游戏对双方是否公平.
专项训练
肆
通关训练
1.(2022·湖北武汉)彩民李大叔购买1张彩票后中奖,这个事件是( )
A.必然事件 B.确定性事件
C.不可能事件 D.随机事件
D
2.(2023·广东)某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹任”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等.小明恰好选中“烹任”的概率为( )
C
3.(2024·广西)不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是( )
D
4.(2023·广西)某班开展“梦想未来、青春有我”主题班会,第一小组有2位男同学和3位女同学,现从中随机抽取1位同学分享个人感悟,则抽到男同学的概率是 .
5.(2023·湖南长沙)千门万户瞳瞳日,总把新桃换旧符.春节是中华民族的传统节日,古人常用写“桃符”的方式来祈福避祸,而现在人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.某商家在春节期间开展商品促销活动,顾客凡购物金额满100元,就可以从“福”字、春联、灯笼这三类礼品中免费领取一件.礼品领取规则:顾客每次从装有大小、形状、质地都相同的三张卡片(分别写有“福”字、春联、灯笼)的不透明袋子中,随机摸出一张卡片,然后领取一件与卡片上文字所对应的礼品,现有2名顾客都只领取了一件礼品,那么他们恰好领取同一类礼品的概率是( )
C
6.(2023·湖南湘潭)为落实“ 双减”政策要求,丰富学生课余生活,某校七年级根据学生需求,组建了四个社团供学生选择:(合唱社团)、(硬笔书法社团)、(街舞社团)、(面点社团).学生从中任意选择两个社团参加活动.
(1)小明对这4个社团都很感兴趣,如果他随机选择两个社团,请列举出所有的可能结果;
(2)小宇和小江在选择过程中,首先都选了社团(街舞社团),第二个社团他俩决定随机选择,请用列表法或树状图求他俩选到相同社团的概率.
6. 解:(1)所有的可能结果共有6种,分别为;
(2)画树状图如下:
共有9种等可能的结果,其中小宇和小江选到相同社团的结果有3种,他俩选到相同社团的概率为.
答案
提升训练
7.(2022·湖北武汉)班长邀请四位同学参加圆桌会议.如图所示,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则两位同学座位相邻的概率是( )
C
8.(2023·福建)为促进消费,助力经济发展,某商场决定“让利酬宾”,于五一期间举办了抽奖促销活动.活动规定:凡在商场消费一定金额的顾客,均可获得一次抽奖机会.抽奖方案如下:从装有大小质地完全相同的1个红球及编号为①②③的3个黄球的袋中,随机摸出1个球,若摸得红球,则中奖,可获得奖品;若摸得黄球,则不中奖.同时,还允许未中奖的顾客将其摸得的球放回袋中,并再往袋中加入1个红球或黄球(它们的大小质地与袋中的4个球完全相同),然后从中随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球,若摸得的两球的颜色相同,则该顾客可获得精美礼品一份.现已知某顾客获得抽奖机会.
(1)求该顾客首次摸球中奖的概率;
(2)假如该顾客首次摸球未中奖,为了有更大机会获得精美礼品,他应往袋中加入哪种颜色的球?说明你的理由.
答案
8. 解:(1)顾客首次摸球的所有可能结果为红,黄①,黄②,黄③,共4种等可能的结果,记“首次摸得红球”为事件,则事件发生的结果只有1种,
,顾客首次摸球中奖的概率为.
(2)他应往袋中加入黄球;理由如下:
记往袋中加入的球为“新”,摸得的两球所有可能的结果列表如下:
共有 20种等可能结果,
①若往袋中加入的是红球,两球颜色相同的结果共有8种,此时该顾客获得精美礼品的概率;②若往袋中加入的是黄球,两球颜色相同的结果共有12种,此时该顾客获得精美礼品的概率;,他应往袋中加入黄球.
课堂练习
伍
1.(2024·盘锦)下列事件是必然事件的是( )
A. 四边形内角和是360°
B. 校园排球比赛,九年一班获得冠军
C. 掷一枚硬币时,正面朝上
D. 打开电视,正在播放神舟十六号载人飞船发射实况
A
2.(2023·大理)在一个不透明的袋子中装有6个白球和14个红球,这些球除颜色外无其他差别,随机从袋子中摸出一个球,则摸到白球的概率为( )
C
A. B. C. D.
3.(2023·湖北襄阳)某校即将举行田 径运动会,“体育达人”小明从“跳高”“跳远” “100米”“400米”四个项目中,随机选择两项,则他选择“100米”与“400米”两个项目的概率是( )
C
A. B. C.
4.(2023·太原)某校在劳动课上,设置了植树、种花、除草三个劳动项目.九(1)班和九(2)班都通过抽签的方式从这三个项目中随机抽取一个项目,则这两个班级恰好都抽到种花的概率是( D )
A. B. C. D.
5.(2024·成都)不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是( )
D
A. C. D.
6.(2024·金华)如图所示,电路连接完好,且各元件工作正常.随机闭合开关,,中的两个,能让两个小灯泡同时发光的概率是( D )
A. B. C. D.
7.(2023·南京)某种绿豆在相同条件下发芽试验的结果如下表所示:
这种绿豆发芽的概率的估计值为 (精确到0.01)
0.93
每批粒数n 2 5 10 50 100 500 1000 1500 2000 3000
发芽的频数m 2 4 9 44 92 463 928 1396 1866 2794
发芽的频率 (精确到0.001) 1.000 0.800 0.900 0.880 0.920 0.926 0.928 0.931 0.933 0.931
8.(2023·杭州)在一个不透明的 口袋中装有红球和白球共12个,这些球除颜色外都相同,将口袋中的球搅匀后,从中随机摸出1个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸球200次,发现有50次摸 到红球,则口袋中红球约有 个.
3
9.(2024·肇庆)我国人工智能市场分为“决策类人工智能”“人工智能机器人”“语音及语义人工智能”“视觉人工智能”四大类型,将四个类型的图标分 别制成四张卡片(卡片背面完全相同),并把 四张卡片背面朝上洗匀,从中随机抽取一张,则抽到“视觉人工智能”的概率为(
10.(2024·广西模拟)我国空间站的主体结构包括核心舱、问天实验舱和梦天实验舱.假设甲、乙、丙三名航天员从核心舱进入实验舱的机会均等,现在要从这三名航天员中选2人进入梦天实验舱开展科学实验,则甲、乙两人同时被选中的概率为 .
11.已知五个红色研学基地,某地为了解中学生的意愿,随机抽取部分学生进行调查,并将统计数据整理后, 绘制了不完整的条形统计图和扇形统计图.
(1)请将条形统计图补充完整;
(2)在扇形统计图中,所在的扇形的圆心角的度数为 ;若该地区有1000名中学生参加研学活动,则愿意去基地的大约有 人;
(3)甲、乙两所学校计划从三个基地中任选一个基地开展研学活动,请利用树状图或表格求两校恰好选取同一个基地的概率.
11. 解:(1)本次抽取的学生有:(人),
其中选择的学生有:(人),
补全的条形统计图如图所示;
答案
答案
(2)在扇形统计图中,所在的扇形的圆心角的度数为:
,
该市有1000名中学生参加研学活动,愿意去A基地的大约有:
(人);
故答案为:14.4°;200;
答案
由上可得,一共有9种等可能性,其中两校恰好选取同一个基地的可能性有3种, ∴两校恰好选取同一个基地的概率为.
12.(2023·承德)“阅读新时代,书 香满宜昌”.在“全民阅读月”活动中,某校提 供了四类适合学生阅读的书籍:文学类,科幻类,漫画类,数理类.为了解学生阅读兴趣,学校随机抽取了部分学生进行调查(每位学生仅选一类).根据收集到的数据,整理后得到下列不完整的图表:
书籍类别 学生人数
A文学类 24
B科幻类 m
C漫画类 16
D数理类 8
(1)本次抽查的学生人数是 ,统计表中的 ;
(2)在扇形统计图中,“漫画类”对应的圆心角的度数是 ;
(3)若该校共有1200名学生,请你估计该校学生选择“数理类”书籍的学生人数;
(4)学校决定成立“文学”“科幻”“漫画” “数理”四个阅读社团.若小文、小明随机选取四个社团中的一个,请利用列表或画树状图的方法,求他们选择同一社团的概率.
答案
答:估计该校学生选择“数理类”书籍的学生人数约为120人;
12.(1)80,32
(2)72°;
(3)1200X=120(人).
答案
由上可得,一共有16种等可能性,其中他们选择同一社团的可能性有4种, ∴他们选择同一社团的概率为.
13.(2023·宁夏)劳动委员统计了某周全班同学的家庭劳动次数x(单位:次),按劳动次数分为4组:,,,,绘制成如图所示的频数分布直方图.从中任选一名同学,则该同学这周家庭劳动次数不足6次的概率是( )
A
A.0.6 B.0.5 C.0.4 D.0.32
14.(2022·靖江)如图所示,一张圆桌共有3个座位,甲、乙,丙3人随机坐到这3个座位上,则甲和乙相邻的概率为( D )
A. B. C. D.1
谢谢观看
同课章节目录
